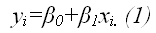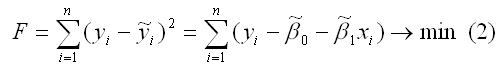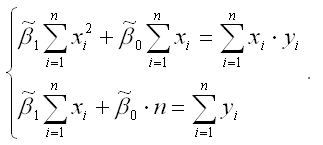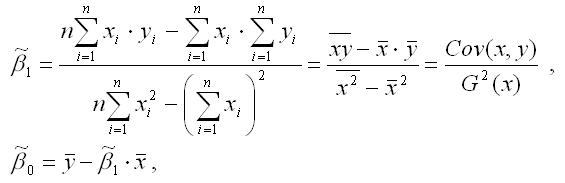Предположим, что в ходе регрессионного анализа была установлена линейная взаимосвязь между исследуемыми переменными х и у, которая описывается моделью регрессии вида:
В результате оценивания данной эконометрической модели определяются оценки неизвестных коэффициентов. Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК).
Метод наименьших квадратов позволяет получить такие оценки параметров β0и β1, при которых сумма квадратов отклонений фактических значений результативного признака y от расчетных (теоретических) y˜ минимальна:
В процессе минимизации функции (1) неизвестными являются только значения коэффициентов β0 и β1, потому что значения результативной и факторной переменных известны из наблюдений. Для определения минимума функции двух переменных вычисляются частные производные этой функции по каждому из оцениваемых параметров и приравниваются к нулю. Результатом данной процедуры будет стационарная система уравнений для функции (2):
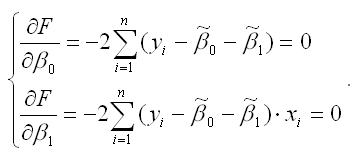
Если разделить обе части каждого уравнения системы на (-2), раскрыть скобки и привести подобные члены, то получим систему нормальных уравнений для функции регрессии вида yi=β0+β1xi:
Если решить данную систему нормальных уравнений, то мы получим искомые оценки неизвестных коэффициентов модели регрессии β0 и β1:
y – среднее значение зависимой переменной;
x – среднее значение независимой переменной;
xy – среднее арифметическое значение произведения зависимой и независимой переменных;
G 2 (x) – дисперсия независимой переменной;
Gcov (x, y) – ковариация между зависимой и независимой переменными.
Таким образом, явный вид решения системы нормальных уравнений может быть записан следующим образом:
- Метод наименьших квадратов
- В чем именно заключается МНК (метод наименьших квадратов)
- Как вывести формулы для вычисления коэффициентов
- Как изобразить МНК на графике функций
- Доказательство метода МНК
- Множественная линейная регрессия. Улучшение модели регрессии
- Понятие множественной линейной регрессии
- Уравнение множественной линейной регрессии и метод наименьших квадратов
- МНК-оценка коэффиентов уравнения множественной регрессии в скалярном виде
- МНК-оценка коэффиентов уравнения множественной регрессии в матричном виде
- Построение наилучшей (наиболее качественной) модели множественной линейной регрессии
- Оценка качества модели множественной линейной регрессии в целом
- Анализ значимости коэффициентов модели множественной линейной регрессии
- Исключение резко выделяющихся наблюдений
- Исключение незначимых переменных из модели
- Нелинейные модели для сравнения
- Применение пошаговых алгоритмов включения и исключения переменных
- Выбор самой качественной модели множественной линейной регрессии
- 🔥 Видео
Видео:Как работает метод наименьших квадратов? Душкин объяснитСкачать

Метод наименьших квадратов
Начнем статью сразу с примера. У нас есть некие экспериментальные данные о значениях двух переменных – x и y . Занесем их в таблицу.
| i = 1 | i = 2 | i = 3 | i = 4 | i = 5 | |
| x i | 0 | 1 | 2 | 4 | 5 |
| y i | 2 , 1 | 2 , 4 | 2 , 6 | 2 , 8 | 3 , 0 |
После выравнивания получим функцию следующего вида: g ( x ) = x + 1 3 + 1 .
Мы можем аппроксимировать эти данные с помощью линейной зависимости y = a x + b , вычислив соответствующие параметры. Для этого нам нужно будет применить так называемый метод наименьших квадратов. Также потребуется сделать чертеж, чтобы проверить, какая линия будет лучше выравнивать экспериментальные данные.
Видео:Метод наименьших квадратов. Линейная аппроксимацияСкачать

В чем именно заключается МНК (метод наименьших квадратов)
Главное, что нам нужно сделать, – это найти такие коэффициенты линейной зависимости, при которых значение функции двух переменных F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 будет наименьшим. Иначе говоря, при определенных значениях a и b сумма квадратов отклонений представленных данных от получившейся прямой будет иметь минимальное значение. В этом и состоит смысл метода наименьших квадратов. Все, что нам надо сделать для решения примера – это найти экстремум функции двух переменных.
Видео:11 4 Применение МНК к решению систем линейных уравненийСкачать

Как вывести формулы для вычисления коэффициентов
Для того чтобы вывести формулы для вычисления коэффициентов, нужно составить и решить систему уравнений с двумя переменными. Для этого мы вычисляем частные производные выражения F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 по a и b и приравниваем их к 0 .
δ F ( a , b ) δ a = 0 δ F ( a , b ) δ b = 0 ⇔ — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) x i = 0 — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) = 0 ⇔ a ∑ i = 1 n x i 2 + b ∑ i = 1 n x i = ∑ i = 1 n x i y i a ∑ i = 1 n x i + ∑ i = 1 n b = ∑ i = 1 n y i ⇔ a ∑ i = 1 n x i 2 + b ∑ i = 1 n x i = ∑ i = 1 n x i y i a ∑ i = 1 n x i + n b = ∑ i = 1 n y i
Для решения системы уравнений можно использовать любые методы, например, подстановку или метод Крамера. В результате у нас должны получиться формулы, с помощью которых вычисляются коэффициенты по методу наименьших квадратов.
n ∑ i = 1 n x i y i — ∑ i = 1 n x i ∑ i = 1 n y i n ∑ i = 1 n — ∑ i = 1 n x i 2 b = ∑ i = 1 n y i — a ∑ i = 1 n x i n
Мы вычислили значения переменных, при который функция
F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 примет минимальное значение. В третьем пункте мы докажем, почему оно является именно таким.
Это и есть применение метода наименьших квадратов на практике. Его формула, которая применяется для поиска параметра a , включает в себя ∑ i = 1 n x i , ∑ i = 1 n y i , ∑ i = 1 n x i y i , ∑ i = 1 n x i 2 , а также параметр
n – им обозначено количество экспериментальных данных. Советуем вам вычислять каждую сумму отдельно. Значение коэффициента b вычисляется сразу после a .
Обратимся вновь к исходному примеру.
Здесь у нас n равен пяти. Чтобы было удобнее вычислять нужные суммы, входящие в формулы коэффициентов, заполним таблицу.
| i = 1 | i = 2 | i = 3 | i = 4 | i = 5 | ∑ i = 1 5 | |
| x i | 0 | 1 | 2 | 4 | 5 | 12 |
| y i | 2 , 1 | 2 , 4 | 2 , 6 | 2 , 8 | 3 | 12 , 9 |
| x i y i | 0 | 2 , 4 | 5 , 2 | 11 , 2 | 15 | 33 , 8 |
| x i 2 | 0 | 1 | 4 | 16 | 25 | 46 |
Решение
Четвертая строка включает в себя данные, полученные при умножении значений из второй строки на значения третьей для каждого отдельного i . Пятая строка содержит данные из второй, возведенные в квадрат. В последнем столбце приводятся суммы значений отдельных строчек.
Воспользуемся методом наименьших квадратов, чтобы вычислить нужные нам коэффициенты a и b . Для этого подставим нужные значения из последнего столбца и подсчитаем суммы:
n ∑ i = 1 n x i y i — ∑ i = 1 n x i ∑ i = 1 n y i n ∑ i = 1 n — ∑ i = 1 n x i 2 b = ∑ i = 1 n y i — a ∑ i = 1 n x i n ⇒ a = 5 · 33 , 8 — 12 · 12 , 9 5 · 46 — 12 2 b = 12 , 9 — a · 12 5 ⇒ a ≈ 0 , 165 b ≈ 2 , 184
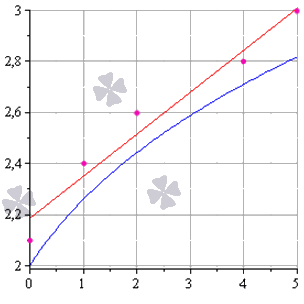
У нас получилось, что нужная аппроксимирующая прямая будет выглядеть как y = 0 , 165 x + 2 , 184 . Теперь нам надо определить, какая линия будет лучше аппроксимировать данные – g ( x ) = x + 1 3 + 1 или 0 , 165 x + 2 , 184 . Произведем оценку с помощью метода наименьших квадратов.
Чтобы вычислить погрешность, нам надо найти суммы квадратов отклонений данных от прямых σ 1 = ∑ i = 1 n ( y i — ( a x i + b i ) ) 2 и σ 2 = ∑ i = 1 n ( y i — g ( x i ) ) 2 , минимальное значение будет соответствовать более подходящей линии.
σ 1 = ∑ i = 1 n ( y i — ( a x i + b i ) ) 2 = = ∑ i = 1 5 ( y i — ( 0 , 165 x i + 2 , 184 ) ) 2 ≈ 0 , 019 σ 2 = ∑ i = 1 n ( y i — g ( x i ) ) 2 = = ∑ i = 1 5 ( y i — ( x i + 1 3 + 1 ) ) 2 ≈ 0 , 096
Ответ: поскольку σ 1 σ 2 , то прямой, наилучшим образом аппроксимирующей исходные данные, будет
y = 0 , 165 x + 2 , 184 .
Видео:Метод наименьших квадратовСкачать

Как изобразить МНК на графике функций
Метод наименьших квадратов наглядно показан на графической иллюстрации. С помощью красной линии отмечена прямая g ( x ) = x + 1 3 + 1 , синей – y = 0 , 165 x + 2 , 184 . Исходные данные обозначены розовыми точками.
Поясним, для чего именно нужны приближения подобного вида.
Они могут быть использованы в задачах, требующих сглаживания данных, а также в тех, где данные надо интерполировать или экстраполировать. Например, в задаче, разобранной выше, можно было бы найти значение наблюдаемой величины y при x = 3 или при x = 6 . Таким примерам мы посвятили отдельную статью.
Видео:Суть метода наименьших квадратов с примерами. Основы эконометрики в RСкачать

Доказательство метода МНК
Чтобы функция приняла минимальное значение при вычисленных a и b , нужно, чтобы в данной точке матрица квадратичной формы дифференциала функции вида F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 была положительно определенной. Покажем, как это должно выглядеть.
У нас есть дифференциал второго порядка следующего вида:
d 2 F ( a ; b ) = δ 2 F ( a ; b ) δ a 2 d 2 a + 2 δ 2 F ( a ; b ) δ a δ b d a d b + δ 2 F ( a ; b ) δ b 2 d 2 b
Решение
δ 2 F ( a ; b ) δ a 2 = δ δ F ( a ; b ) δ a δ a = = δ — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) x i δ a = 2 ∑ i = 1 n ( x i ) 2 δ 2 F ( a ; b ) δ a δ b = δ δ F ( a ; b ) δ a δ b = = δ — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) x i δ b = 2 ∑ i = 1 n x i δ 2 F ( a ; b ) δ b 2 = δ δ F ( a ; b ) δ b δ b = δ — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) δ b = 2 ∑ i = 1 n ( 1 ) = 2 n
Иначе говоря, можно записать так: d 2 F ( a ; b ) = 2 ∑ i = 1 n ( x i ) 2 d 2 a + 2 · 2 ∑ x i i = 1 n d a d b + ( 2 n ) d 2 b .
Мы получили матрицу квадратичной формы вида M = 2 ∑ i = 1 n ( x i ) 2 2 ∑ i = 1 n x i 2 ∑ i = 1 n x i 2 n .
В этом случае значения отдельных элементов не будут меняться в зависимости от a и b . Является ли эта матрица положительно определенной? Чтобы ответить на этот вопрос, проверим, являются ли ее угловые миноры положительными.
Вычисляем угловой минор первого порядка: 2 ∑ i = 1 n ( x i ) 2 > 0 . Поскольку точки x i не совпадают, то неравенство является строгим. Будем иметь это в виду при дальнейших расчетах.
Вычисляем угловой минор второго порядка:
d e t ( M ) = 2 ∑ i = 1 n ( x i ) 2 2 ∑ i = 1 n x i 2 ∑ i = 1 n x i 2 n = 4 n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2
После этого переходим к доказательству неравенства n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 > 0 с помощью математической индукции.
- Проверим, будет ли данное неравенство справедливым при произвольном n . Возьмем 2 и подсчитаем:
2 ∑ i = 1 2 ( x i ) 2 — ∑ i = 1 2 x i 2 = 2 x 1 2 + x 2 2 — x 1 + x 2 2 = = x 1 2 — 2 x 1 x 2 + x 2 2 = x 1 + x 2 2 > 0
У нас получилось верное равенство (если значения x 1 и x 2 не будут совпадать).
- Сделаем предположение, что данное неравенство будет верным для n , т.е. n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 > 0 – справедливо.
- Теперь докажем справедливость при n + 1 , т.е. что ( n + 1 ) ∑ i = 1 n + 1 ( x i ) 2 — ∑ i = 1 n + 1 x i 2 > 0 , если верно n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 > 0 .
( n + 1 ) ∑ i = 1 n + 1 ( x i ) 2 — ∑ i = 1 n + 1 x i 2 = = ( n + 1 ) ∑ i = 1 n ( x i ) 2 + x n + 1 2 — ∑ i = 1 n x i + x n + 1 2 = = n ∑ i = 1 n ( x i ) 2 + n · x n + 1 2 + ∑ i = 1 n ( x i ) 2 + x n + 1 2 — — ∑ i = 1 n x i 2 + 2 x n + 1 ∑ i = 1 n x i + x n + 1 2 = = ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 + n · x n + 1 2 — x n + 1 ∑ i = 1 n x i + ∑ i = 1 n ( x i ) 2 = = ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 + x n + 1 2 — 2 x n + 1 x 1 + x 1 2 + + x n + 1 2 — 2 x n + 1 x 2 + x 2 2 + . . . + x n + 1 2 — 2 x n + 1 x 1 + x n 2 = = n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 + + ( x n + 1 — x 1 ) 2 + ( x n + 1 — x 2 ) 2 + . . . + ( x n — 1 — x n ) 2 > 0
Выражение, заключенное в фигурные скобки, будет больше 0 (исходя из того, что мы предполагали в пункте 2 ), и остальные слагаемые будут больше 0 , поскольку все они являются квадратами чисел. Мы доказали неравенство.
Ответ: найденные a и b будут соответствовать наименьшему значению функции F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 , значит, они являются искомыми параметрами метода наименьших квадратов (МНК).
Видео:Метод наименьших квадратов (МНК)Скачать
Множественная линейная регрессия. Улучшение модели регрессии
Видео:Метод Наименьших Квадратов (МНК)Скачать

Понятие множественной линейной регрессии
Множественная линейная регрессия — выраженная в виде прямой зависимость среднего значения величины Y от двух или более других величин X 1 , X 2 , . X m . Величину Y принято называть зависимой или результирующей переменной, а величины X 1 , X 2 , . X m — независимыми или объясняющими переменными.
В случае множественной линейной регрессии зависимость результирующей переменной одновременно от нескольких объясняющих переменных описывает уравнение или модель

где 

Функция множественной линейной регрессии для выборки имеет следующий вид:

где 

Видео:Метод наименьших квадратов. Квадратичная аппроксимацияСкачать

Уравнение множественной линейной регрессии и метод наименьших квадратов
Коэффициенты модели множественной линейной регресии, так же, как и для парной линейной регрессии, находят при помощи метода наименьших квадратов.
Разумеется, мы будем изучать построение модели множественной регрессии и её оценивание с использованием программных средств. Но на экзамене часто требуется привести формулы МНК-оценки (то есть оценки по методу наименьших квадратов) коэффициентов уравнения множественной линейной регрессии в скалярном и в матричном видах.
МНК-оценка коэффиентов уравнения множественной регрессии в скалярном виде
Метод наименьших квадратов позволяет найти такие значения коэффициентов, что сумма квадратов отклонений будет минимальной. Для нахождения коэффициентов решается система нормальных уравнений
Решение системы можно получить, например, методом Крамера:

Определитель системы записывается так:
МНК-оценка коэффиентов уравнения множественной регрессии в матричном виде
Данные наблюдений и коэффициенты уравнения множественной регрессии можно представить в виде следующих матриц:
Формула коэффициентов множественной линейной регрессии в матричном виде следующая:

где 


Решая это уравнение, мы получим матрицу-столбец b, элементы которой и есть коэффициенты уравнения множественной линейной регрессии, для нахождения которых и был изобретён метод наименьших квадратов.
Видео:Построение уравнения линейной регрессии методом наименьших квадратов.Скачать

Построение наилучшей (наиболее качественной) модели множественной линейной регрессии
Пусть при обработке данных некоторой выборки в пакете программных средств STATISTICA получена первоначальная модель множественной линейной регрессии. Предстоит проанализировать полученную модель и в случае необходимости улучшить её.
Качество модели множественной линейной регрессии оценивается по тем же показателям качества, что и в случае модели парной линейной регрессии: коэффициент детерминации 

Важный показатель качества модели линейной регрессии — проверка на выполнение требований Гаусса-Маркова к остаткам. В качественной модели линейной регрессии выполняются все условия Гаусса-Маркова:
- условие 1: математическое ожидание остатков равно нулю для всех наблюдений ( ε(e i ) = 0 );
- условие 2: теоретическая дисперсия остатков постоянна (равна константе) для всех наблюдений ( σ²(e i ) = σ²(e i ), i = 1, . n );
- условие 3: отсутствие систематической связи между остатками в любых двух наблюдениях;
- условие 4: отсутствие зависимости между остатками и объясняющими (независимыми) переменными.
В случае выполнения требований Гаусса-Маркова оценка коэффициентов модели, полученная методом наименьших квадратов является
Затем необходимо провести анализ значимости отдельных переменных модели множественной линейной регрессии с помощью критерия Стьюдента.
В случае наличия резко выделяющихся наблюдений (выбросов) нужно последовательно по одному исключить их из модели и проанализировать наличие незначимых переменных в модели и, в случае необходимости исключить их из модели по одному.
В исследованиях поведения человека, как и во многих других, чтобы они претендовали на объективность, важно не только установить зависимость между факторами, но и получить все необходимые статистические показатели для результата проверки соответствующей гипотезы.
Кроме того, требуется на основе тех же данных построить две нелинейные модели регрессии — с квадратами двух наиболее значимых переменных и с логарифмами тех же наиболее значимых переменных. Они также будут сравниваться с линейными моделями, полученных на разных шагах.
Также требуется построить модели с применением пошаговых процедур включения (FORWARD STEPWISE) и исключения (BACKWARD STEPWISE).
Все полученные модели множественной регрессии нужно сравнить и выбрать из них наилучшую (наиболее качественную). Теперь разберём перечисленные выше шаги последовательно и на примере.
Видео:Метод наименьших квадратов, урок 1/2. Линейная функцияСкачать
Оценка качества модели множественной линейной регрессии в целом
Пример. Задание 1. Получено следующее уравнение множественной линейной регрессии:
и следующие показатели качества описываемой этим уравнением модели:
 | adj. | RSS | SEE | F | p-level |
| 0,426 | 0,279 | 2,835 | 1,684 | 2,892 | 0,008 |
Сделать вывод о качестве модели в целом.
Ответ. По всем показателям модель некачественная. Значение 

Для анализа на выполнение условий Гаусса-Маркова воспользуемся диаграммой рассеивания наблюдений (для увеличения рисунка щёлкнуть по нему левой кнопкой мыши):
Результаты проверки графика показывают: условие равенства нулю математического ожидания остатков выполняется, а условие на постоянство дисперсии — не выполняется. Достаточно невыполнения хотя бы одного условия Гаусса-Маркова, чтобы заключить, что оценка коэффициентов модели линейной регрессии не является несмещённой, эффективной и состоятельной.
Видео:Основы параметрической формы метода наименьших квадратов (МНК) на примере уравнивания опорных сетей.Скачать

Анализ значимости коэффициентов модели множественной линейной регрессии
С помощью критерия Стьюдента проверяется гипотеза о том, что соответствующий коэффициент незначимо отличается от нуля, и соответственно, переменная при этом коэффициенте имеет незначимое влияние на зависимую переменную. В свою очередь, в колонке p-level выводится вероятность того, что основная гипотеза будет принята. Если значение p-level больше уровня значимости α, то основная гипотеза принимается, иначе – отвергается. В нашем примере установлен уровень значимости α=0,05.
Пример. Задание 2. Получены следующие значения критерия Стьюдента (t) и p-level, соответствующие переменным уравнения множественной линейной регрессии:
| Перем. | Знач. коэф. | t | p-level |
| X1 | 0,129 | 2,386 | 0,022 |
| X2 | -0,286 | -2,439 | 0,019 |
| X3 | -0,037 | -0,238 | 0,813 |
| X4 | 0,15 | 1,928 | 0,061 |
| X5 | 0,328 | 0,548 | 0,587 |
| X6 | -0,391 | -0,503 | 0,618 |
| X7 | -0,673 | -0,898 | 0,375 |
| X8 | -0,006 | -0,07 | 0,944 |
| X9 | -1,937 | -2,794 | 0,008 |
| X10 | -1,233 | -1,863 | 0,07 |
Сделать вывод о значимости коэффициентов модели.
Ответ. В построенной модели присутствуют коэффициенты, которые незначимо отличаются от нуля. В целом же у переменной X8 коэффициент самый близкий к нулю, а у переменной X9 — самое высокое значение коэффициента. Коэффициенты модели линейной регрессии можно ранжировать по мере убывания незначимости с возрастанием значения t-критерия Стьюдента.
Видео:Системы одновременных эконометрических уравненийСкачать

Исключение резко выделяющихся наблюдений
Пример. Задание 3. Выявлены несколько резко выделяющихся наблюдений (выбросов, то есть наблюдений с нетипичными значениями): 10, 3, 4 (соответствуют строкам исходной таблицы данных). Эти наблюдения следует последовательно исключить из модели и по мере исключения заполнить таблицу с показателями качества модели. Исключили наблюдение 10 — заполнили значение показателей, далее исключили наблюдение 3 — заполнили и так далее. По мере исключения STATISTICA будет выдавать переменные, которые остаются значимыми в модели множественной линейной регрессии — они будут выделены красном цветом. Те, что не будут выделены красным цветом — незначимые переменные и их также нужно внести в соответствующую ячейку таблицы. По завершении исключения выбросов записать уравнение конечной множественной линейной регрессии.
| № | adj. | SEE | F | p- level | незнач. пер. |
| 10 | 0,411 | 2,55 | 2,655 | 0,015 | X3, X4, X5, X6, X7, X8, X10 |
| 3 | 0,21 | 2,58 | 2,249 | 0,036 | X3, X4, X5, X6, X7, X8, X10 |
| 4 | 0,16 | 2,61 | 1,878 | 0,082 | X3, X4, X5, X6, X7, X8, X10 |
Уравнение конечной множественной линейной регрессии:
Случается однако, когда после исключения некоторого наблюдения исключение последующих наблюдений приводит к ухудшению показателей качества модели. Причина в том, что с исключением слишком большого числа наблюдений выборка теряет информативность. Поэтому в таких случаях следует вовремя остановиться.
Видео:ЦОС Python #1: Метод наименьших квадратовСкачать

Исключение незначимых переменных из модели
Пример. Задание 4. По мере исключения из модели множественной линейной регрессии переменных с незначимыми коэффициентами (получены при выполнении предыдущего задания, занесены в последнюю колонку таблицы) заполнить таблицу с показателями качества модели. Последняя колонка, обозначенная звёздочкой — список переменных, имеющих значимое влияние на зависимую переменную. Эти переменные STATISTICA будет выдавать выделенными красным цветом. По завершении исключения незначимых переменных записать уравнение конечной множественной линейной регрессии.
| Искл. пер. | adj. | SEE | F | p- level | * |
| X3 | 0,18 | 1,71 | 2,119 | 0,053 | X4, X5, X6, X7, X8, X10 |
| X4 | 0,145 | 1,745 | 1,974 | 0,077 | X5, X6, X7, X8, X10 |
| X5 | 0,163 | 2,368 | 2,282 | 0,048 | X6, X7, X8, X10 |
| X6 | 0,171 | 2,355 | 2,586 | 0,033 | X7, X8, X10 |
| X7 | 0,167 | 2,223 | 2,842 | 0,027 | X8, X10 |
| X8 | 0,184 | 1,705 | 3,599 | 0,013 | X10 |
Когда осталась одна переменная, имеющая значимое влияние на зависимую переменную, больше не исключаем переменные, иначе получится, что в модели все переменные незначимы.
Уравнение конечной множественной линейной регрессии после исключения незначимых переменных:
Переменные X1 и X2 в задании 3 не вошли в список незначимых переменных, поэтому они вошли в уравнение конечной множественной линейной регрессии «автоматически».
Видео:Обработка результатов эксперимента. 8. Метод минимума хи-квадрат и МНКСкачать

Нелинейные модели для сравнения
Пример. Задание 5. Построить две нелинейные модели регрессии — с квадратами двух наиболее значимых переменных и с логарифмами тех же наиболее значимых переменных.
Так как в наблюдениях переменных X9 и X10 имеется 0, а натуральный логарифм от 0 вычислить невозможно, то берутся следующие по значимости переменные: X1 и X2.
Полученное уравнение нелинейной регрессии с квадратами двух наиболее значимых переменных:
Показатели качества первой модели нелинейной регрессии:
 | adj. | RSS | SEE | F | p-level |
| 0,17 | 0,134 | 159,9 | 1,845 | 4,8 | 0,0127 |
Вывод: модель некачественная, так как RSS и SEE принимают высокие значения, p-level стремится к нулю, коэффициент детерминации незначимо отличается от нуля.
Полученное уравнение нелинейной регрессии с логарифмами двух наиболее значимых переменных:
Показатели качества второй модели нелинейной регрессии:
 | adj. | RSS | SEE | F | p-level |
| 0,182 | 0,148 | 157,431 | 1,83 | 5,245 | 0 |
Вывод: модель некачественная, так как RSS и SEE принимают высокие значения, p-level стремится к нулю, коэффициент детерминации незначимо отличается от нуля.
Видео:МНК. Пример 2. Парная регрессияСкачать

Применение пошаговых алгоритмов включения и исключения переменных
Пример. Задание 6. Настроить пакет STATISTICA для применения пошаговых процедур включения (FORWARD STEPWISE) и исключения (BACKWARD STEPWISE). Для этого в диалоговом окне MULTIPLE REGRESSION указать Advanced Options (stepwise or ridge regression). В поле Method выбрать либо Forward Stepwise (алгоритм пошагового включения), либо Backward Stepwise (алгоритм пошагового исключения). Необходимо настроить следующие параметры:
- в окне Tolerance необходимо установить критическое значение для уровня толерантности (оставить предложенное по умолчанию);
- в окне F-remove необходимо установить критическое значение для статистики исключения (оставить предложенное по умолчанию);
- в окне Display Results необходимо установить режим At each step (результаты выводятся на каждом шаге процедуры).
Построить, как описано выше, модели множественной линейной регрессии автоматически.
В результате применения пошагового алгоритма включения получено следующее уравнение множественной линейной регрессии:
Показатели качества модели нелинейной регрессии, полученной с применением пошаговой процедуры включения:
 | adj. | RSS | SEE | F | p-level |
| 0,41 | 0,343 | 113,67 | 1,61 | 6,11 | 0,002 |
В результате применения пошагового алгоритма исключения получено следующее уравнение множественной линейной регрессии:
Показатели качества модели нелинейной регрессии, полученной с применением пошаговой процедуры исключения:
 | adj. | RSS | SEE | F | p-level |
| 0,22 | 0,186 | 150,28 | 1,79 | 6,61 | 0 |
Видео:Математика #1 | Корреляция и регрессияСкачать

Выбор самой качественной модели множественной линейной регрессии
Пример. Задание 7. Сравнить модели, полученные на предыдущих шагах и определить самую качественную.
| Модель | Ручная | Кв. перем. | Лог. перем. | forward stepwise | backward stepwise |
 | 0,255 | 0,17 | 0,182 | 0,41 | 0,22 |
adj. | 0,184 | 0,134 | 0,148 | 0,343 | 0,186 |
| RSS | 122,01 | 159,9 | 157,43 | 113,67 | 150,28 |
| SEE | 1,705 | 1,845 | 1,83 | 1,61 | 1,79 |
| F | 3,599 | 4,8 | 5,245 | 6,11 | 6,61 |
| p-level | 0,013 | 0,0127 | 0 | 0,002 | 0 |
Самая качественная модель множественной линейной регрессии — модель, построенная методом FORWARD STEPWISE (пошаговое включение переменных), так как коэффициент детерминации у неё самый высокий, а RSS и SEE наименьшие в сравнении значений оценок качества других регрессионных моделей.
🔥 Видео
Метод наименьших квадратов. ТемаСкачать

Коэффициент детерминации. Основы эконометрикиСкачать

Метод наименьших квадратов. Регрессионный анализ.Скачать

Аппроксимация измерений по методу наименьших квадратовСкачать