Метрология основное уравнение метрологии основной постулат метрологии (6 видео)

Основы теории измерений. Основной постулат метрологии. Уравнения и шкалы измерений. Приведите примеры использования шкал измерений

Средством измерения (СИ)называется техническое средство, предназначенное для измерений, имеющее нормированные метрологические характеристики, воспроизводящее и хранящее единицу физической величины, размер которой принимается неизменным (в пределах установленной погрешности) в течение известного интервала времени.

Средства измерения классифицируют по следующим признакам:

по конструктивному исполнению;

По конструктивному исполнению СИ подразделяются на: меры, измерительные приборы, измерительные преобразователи, измерительные установки, измерительные системы.

Первым постулатом теории измерений является постулат А: в рамках принятой модели объекта исследования существует определенная физическая величина и ее истинное значение.
А1: для данной физической величины объекта измерения существует множество измеряемых величин (и соответственно их истинных значений).

В: истинное значение измеряемой величины постоянно.

В1:для измерения переменной физической величины необходимо определить ее постоянный параметр – измеряемую величину.

С: существует несоответствие измеряемой величины исследуемому свойству объекта (пороговое несоответствие измеряемой величины).

С1: истинное значение измеряемой величины отыскать невозможно.

С2: достижимая точность измерения определяется априорной информацией об объекте измерения.

Шкалой измерений называют порядок определения и обозначения возможных значений конкретной величины или проявлений какого-либо свойства. Понятия шкалы возникли в связи с необходимостью изучать не только количественные, но и качественные свойства природных и рукотворных объектов и явлений.
Различают несколько типов шкал.
1. Шкала наименований (классификации) – это самая простая шкала, которая основана на приписывании объекту знаков или цифр для их идентификации или нумерации.
2. Шкала порядка (ранжирования) —упорядочивает объекты относительно какого-либо их свойства в порядке убывания или возрастания, например, землетрясений, силы ветра.
3. Шкала интервалов (разностей) содержит разность значений физической величины.
4. Шкала отношений — это шкала интервалов с естественным (не условным) нулевым значением и принятые по соглашению единицы измерений.
5. Абсолютные шкалы — это шкалы отношений, в которых однозначно (а не по соглашению) присутствует определение единицы измерения.
6. Условные шкалы — шкалы, исходные значения которых выражены в условных единицах. К таким шкалам относятся шкалы наименований и порядка.

Примером из шкалы мнтервалов такой шкалы являются различные шкалы времени, начало которых выбрано по соглашению (от Рождества Христова, от переселения пророка Мухаммеда из Мекки в Медину). Другими примерами шкалы интервалов являются шкала расстояний и температурная шкала Цельсия. Результаты измерений по этой шкале (разности) можно складывать и вычитать.

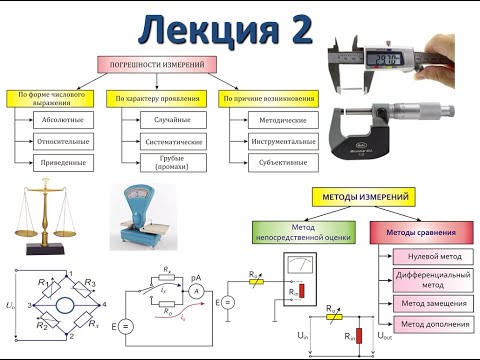
29.Погрешности. Классификация. Причины возникновения, способы обнаружения, пути устранения. Приведите пример обнаружения погрешностей. (+правило трех сигм)

Погрешность измерения — оценка отклонения измеренного значения величины от её истинного значения. Погрешность измерения является характеристикой (мерой) точности измерения.

Классификация погрешностей по способу выражения (абс., отн., привед.) и по влиянию внешних условий (осн. и дополн.)
^ Абсолютная погрешность– это значение, вычисляемое как разность между значением величины, полученным в процессе измерений, и настоящим (действительным) значением данной величины.
^ Абсолютная погрешность меры– это значение, вычисляемое как разность между числом, являющимся номинальным значением меры, и настоящим (действительным) значением воспроизводимой мерой величины.
^ Относительная погрешность– это число, отражающее степень точности измерения.
Приведенная погрешность– это значение, вычисляемое как отношение значения абсолютной погрешности к нормирующему значению.
^ Инструментальная погрешность– это погрешность, возникающая из-за допущенных в процессе изготовления функциональных частей средств измерения ошибок.
^ Методическая погрешность– это погрешность, возникающая по следующим причинам:
1) неточность построения модели физического процесса, на котором базируется средство измерения;
2) неверное применение средств измерений.
^ Субъективная погрешность– это погрешность возникающая из-за низкой степени квалификации оператора средства измерений, а также из-за погрешности зрительных органов человека, т. е. причиной возникновения субъективной погрешности является человеческий фактор.
^ Статическая погрешность– это погрешность, которая возникает в процессе измерения постоянной (не изменяющейся во времени) величины.
Динамическая погрешность– это погрешность, численное значение которой вычисляется как разность между погрешностью, возникающей при измерении непостоянной (переменной во времени) величины, и статической погрешностью (погрешностью значения измеряемой величины в определенный момент времени).
^ Аддитивная погрешность– это погрешность, возникающая по причине суммирования численных значений и не зависящая от значения измеряемой величины, взятого по модулю (абсолютного).
^ Мультипликативная погрешность– это погрешность, изменяющаяся вместе с изменением значений величины, подвергающейся измерениям.
Систематическая погрешность– это составная часть всей погрешности результата измерения, не изменяющаяся или изменяющаяся закономерно при многократных измерениях одной и той же величины.
^ Случайная погрешность– это составная часть погрешности результата измерения, изменяющаяся случайно, незакономерно при проведении повторных измерений одной и той же величины.

Погрешности метода возникают также при экстраполяции свойства, измеренного на ограниченной части некоторого объекта, на весь объект, если последний не обладает однородностью измеряемого свойства. Так, считая диаметр цилиндрического вала равным результату, полученному при измерении в одном сечении и в одном направлении, мы допускаем систематическую погрешность, полностью определяемую отклонениями формы исследуемого вала. При определении плотности вещества по измерениям массы и объема некоторой пробы возникает систематическая погрешность, если проба содержала некоторое количество примесей, а результат измерения принимается за характеристику данного вещества вообще.

К погрешностям метода следует отнести также те погрешности, которые возникают вследствие влияния измерительной аппаратуры на измеряемые свойства объекта. Подобные явления возникают, например, при измерении длин, когда измерительное усилие используемых приборов достаточно велико, при регистрации быстропротекающих процессов недостаточно быстродействующей аппаратурой, при измерениях температур жидкостными или газовыми термометрами и так далее.

Способ обнаружения погрешностей:Либо математическим уравнением,либо Одним из наиболее действенных способов обнаружения систематических погрешностей в ряде результатов наблюдений является построение графика последовательности неисправленных значений случайных отклонений результатов наблюдений от средних арифметических.

Содержание

Основные постулаты метрологии. СХЕМА ПОЛУЧЕНИЯ И ИСПОЛЬЗОВАНИЯ КОЛИЧЕСТВЕННОЙ ИНФОРМАЦИИ. — презентация
Похожие презентации
Презентация на тему: » Основные постулаты метрологии. СХЕМА ПОЛУЧЕНИЯ И ИСПОЛЬЗОВАНИЯ КОЛИЧЕСТВЕННОЙ ИНФОРМАЦИИ.» — Транскрипт:
Основной постулат метрологии
Основной постулат метрологии
🎬 Видео

Видео:Лекция 2. Метрология, стандартизация и сертификация. 2021Скачать

Основные постулаты метрологии. СХЕМА ПОЛУЧЕНИЯ И ИСПОЛЬЗОВАНИЯ КОЛИЧЕСТВЕННОЙ ИНФОРМАЦИИ. — презентация

Презентация была опубликована 3 года назад пользователемСымбат Кулбаева

Презентация на тему: » Основные постулаты метрологии. СХЕМА ПОЛУЧЕНИЯ И ИСПОЛЬЗОВАНИЯ КОЛИЧЕСТВЕННОЙ ИНФОРМАЦИИ.» — Транскрипт:

1 Основные постулаты метрологии

2 СХЕМА ПОЛУЧЕНИЯ И ИСПОЛЬЗОВАНИЯ КОЛИЧЕСТВЕННОЙ ИНФОРМАЦИИ

3 Постулат Постулат — утверждение, принимаемое без доказательств и служащее основой для построения какой-либо научной теории аксиома — это утверждение, в рамках теории принимаемое истинным без доказательств; аксиома — положение, принимаемое без логических доказательств в силу непосредственной убедительности» (БСЭ). Требования к постулатам (аксиомам): — Набор аксиом должен быть полным (исчерпывающим) и непротиворечивым. -Аксиомы должны быть независимыми, т.е. не выдвигаться одна из другой. -Аксиомы должны устанавливаться как однозначно понимаемый результат эмпирического опыта (наблюдение, эксперимент, исследование), т.к. теория должна быть адекватной, а ее результаты – верифицируемы. Требования к научной дисциплине как к специфической области научного знания — специфический предмет изучения. — цель, заключающаяся в описании, объяснении и предсказании процессов и явлений действительности, составляющих предмет ее изучения. — специфическая проблематика. — свой понятийный аппарат. — специфические и заимствованные из других наук методы и средства достижения цели и построения доказательств. Научная дисциплина должна также удовлетворять требованиям внутренней непротиворечивости, адекватности (описание и объяснение наблюдаемых свойств предмета изучения) и перспективности (предсказание не наблюдаемых свойств предмета изучения). О постулатах и аксиомах метрологии

4 ПРОБЛЕМЫ ТЕОРЕТИЧЕСКОЙ МЕТРОЛОГИИ -К основным проблемам теоретической метрологии относят создание и разработку: — физических основ единиц ФВ, шкал и систем единиц, необходимых для реализации измерений. — математическая обработка и представление результатов измерений. учения об основных понятиях и исходных положениях — учения об основных понятиях и исходных положениях; -основ метрологического исследования, построения метрологических цепей (метрологические характеристики, метрологическая надежность СИ); — теории точности измерений (точность средства и результата измерения, достижимая точность измерения ФВ); — теории эталонов единиц ФВ и передачи размеров единиц ФВ; — теории построения системы метрологического обеспечения. 4

5 Формулировка основных постулатов метрологии Первый постулат метрологии П.1 В рамках принятой модели исследования существует определенная измеряемая ФВ и ее истинное значение Сл.: Для данной ФВ существует множество измеряемых величин Существует истинное значение физической величины, которую мы измеряем. Существует истинное значение физической величины, которую мы измеряем. Из 1-го постулата следует, что истинное значение физической величины – это значение, которое идеальным образом отражает в качественном и в количественном отношениях соответствующее свойство объекта измерений; А.1 Между состояниями данной характеристики и между значениями соответствующих величин существует отношение изоморфности (т.е. эти состояния «одинаково устроены» или «эквивалентны»)

6 Формулировка основных постулатов метрологии Второй – основной постулат метрологии П.2 Истинное значение физической величины определить невозможно, оно существует только в рамках принятых моделей. П.2 Существует несоответствие измеряемой величины исследуемому свойству объекта Сл.1: Истинное значение величины отыскать невозможно Сл.2: Достижимая точность измерений определяется априорной информацией об объекте измерения 2-я Аксиома метрологии 2-я Аксиома метрологии Неоднозначность отображения состояния в образ состояния, реализованного с помощью измерительного средства, можно установить на основе математической модели, описывающей метрологические качества этого средства

7 Вывод из 2-го постулата: несовершенство средств и методов измерений, недостаточная тщательность проведения измерений и обработки их результатов, воздействие внешних дестабилизирующих факторов, дороговизна. Трудоемкость и длительность измерений не позволяют получить при измерении истинного значения физической величины. В большинстве случаев достаточно знать действительное значение измеряемой физической величины — значение, найденное экспериментальным путем и настолько приближающееся к истинному значению, что для данных целей может быть использовано вместо него. Т.О. Основным принят 2-й постулат: Измеряемая физическая величина и её истинное значение существуют только в рамках принятой теоретической модели исследования (объекта измерения).

8 Формулировка основных постулатов метрологии П.3 Истинное значение физической величины постоянно. А.3 Отображение состояния данной характеристики в образ состояния неоднозначно (это – отображение точки в отдельное множество) Из этого постулата логически вытекает, что для практики достаточно знать погрешность результата измерения – алгебраическую разность между полученным при измерении и действительным значениями измеряемой величины. Третий постулат и аксиома метрологии

9 ОСНОВНОЕ УРАВНЕНИЯ ИЗМЕРЕНИЯ и погрешность измерений Измерительное преобразование формально описать основным уравнением измерения: Q = Nq, Х=q[Х] где Q – измеряемая величина; q – единица измеряемой величины; N – числовое значение, определяющее соотношение между Q и q. любой объект измерения характеризуется некоторым множеством физических величин: (ФВ1. ФВn, или Q1. Qn) = х – Q, где – погрешность измерения, х – результат измерения (полученное при измерении значение физической величины), Q – истинное значение физической величины. Δ

х – Ад Ад – действительное значение физической величины 9

10 Математическая формулировка основного постулата метрологии основное уравнение измерения, где q числовое значение, [Q] единица измеряемой величины. процедура сравнения, учитывающая невозможность непосредственного сравнения с мерой (например, для жидкостей при взвешивании). процедура сравнения, учитывающая необходимость увеличения при микро- и нано измерениях. математическая модель измерения по шкале отношений (без учёта мультипликативных факторов). упрощенная процедура сравнения неизвестным

11 Отсчет является случайным числом. На этом постулате, который легко поддается проверке и остается справедливым в любых областях и видах измерений, основана вся метрология. Отсчет в ней не может быть представлен одним числом. Его можно лишь описать словами или математическими символами, представить массивом экспериментальных данных, таблично, графически, аналитическим выражением и т.п. Пример 1. При — кратном независимом измерении одной и той же физической величины постоянного размера на световом табло цифрового измерительного прибора в случайном порядке появлялись числа, представленные в первой графе таблицы (См. следующий слайд)

12 Таблица — Результаты наблюдений и статистические характеристики

13 Распределение вероятности отсчета цифрового измерительного прибора (графическая иллюстрация результатов таблицы)

14 Функция распределения вероятности отсчета цифрового измерительного прибора

15 Таким образом, как распределение вероятности, так и функция распределения вероятности являются исчерпывающим описанием отсчета у цифровых измерительных приборов любой конструкции.

16 Пример 2, иллюстрирующий справедливость и универсальность основного постулата метрологии При -кратном независимом измерении одной и той же физической величины постоянного размера аналоговым измерительным прибором указатель отсчетного устройства в случайной последовательности по m раз останавливался на каждом из делений шкалы (см. следующий слайд) . Что представляет собой отсчет при таком измерении?

17 Результаты отсчета и частота их появления:

18 Гистограмма, полигон частот Как гистограмма, так и полигон являются исчерпывающим эмпирическим описанием отсчета у аналоговых измерительных приборов любой конструкции.

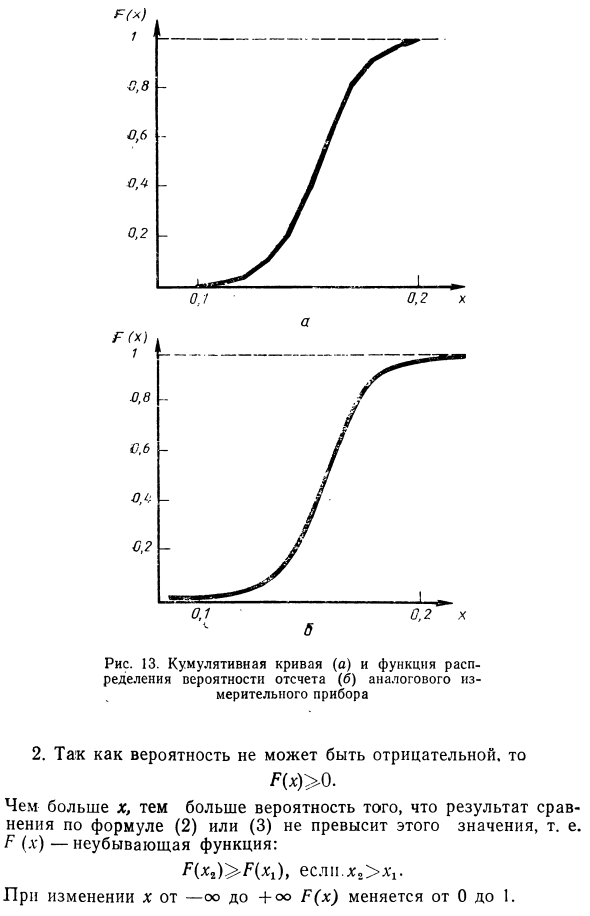
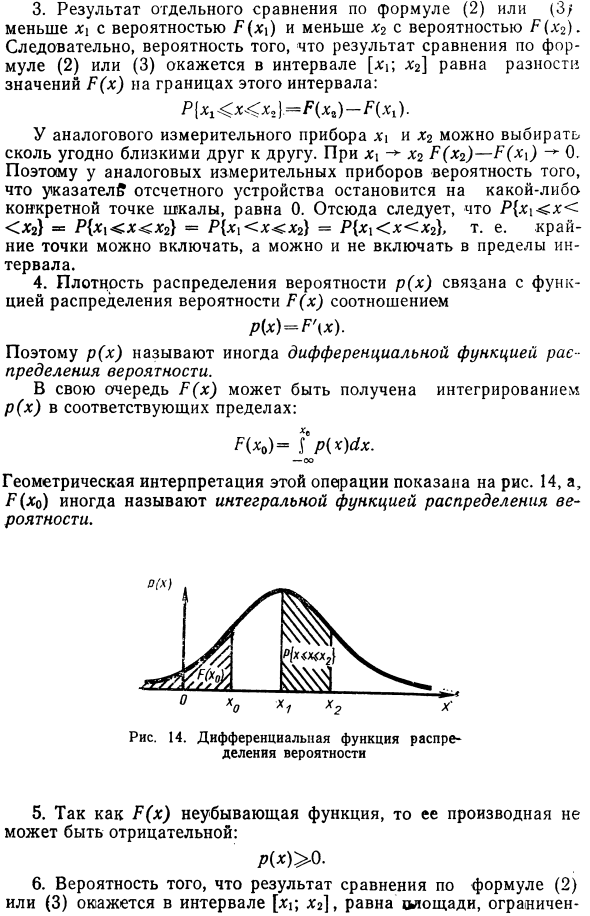
19 Если бы была возможность увеличивать количество измерений, то в пределе (т.е., при стремлении к бесконечному числу измерений) полигон перешел бы в кривую плотности распределения вероятности отсчета, показанную на рисунке б. При подсчете сколько раз указатель отсчетного устройства останавливался левее каждой отметки шкалы, откладывая над этой отметкой вдоль оси ординат отношение числа таких отклонений к их общему числу и соединяя полученные точки отрезками прямых — ломаную линию, называемую кумулятивной кривой.

20 Таким образом, плотность распределения вероятности и функция распределения вероятности служат в теории вероятности моделями эмпирических законов распределения, получаемых из экспериментальных данных методами математической статистики.

21 Решение основного уравнения измерений для шкалы отношений

22 Результат многократного измерения по шкале отношений

23 Математические модели основного постулата метрологии по шкалам интервалов и порядка Модель измерений по шкале интервала Модель измерений по шкале порядка Модель измерений по шкале порядка описывает процедуру сравнения двух размеров одной и той измеряемой величины. Результат- решение о том, какой из размеров больше, либо они равны. 1=01=2

24 Первый прибор Второй прибор U, BU 2, B 2 U, BU 2, B РЕЗУЛЬТАТЫ ИЗМЕРЕНИЯ НАПРЯЖЕНИЯ РАЗЛИЧНЫМИ ВОЛЬТМЕТРАМИ

25 ПУТИ ПОВЫШЕНИЯ ТОЧНОСТИ ИЗМЕРЕНИЙ

26 СХЕМА ПОЛУЧЕНИЯ И ИСПОЛЬЗОВАНИЯ КОЛИЧЕСТВЕННОЙ ИНФОРМАЦИИ

29 Принцип неопределенности Найквиста. Принцип взаимодействия прибора и объекта измерения. Принцип несовершенства полезных сигналов. Принцип технологического несовершенства приборов. Принцип несовершенства материалов. Принцип воздействия внешних возмущений на прибор. Принцип генерирования возмущений внутри прибора. Принцип несовершенства технологии измерения. вектор выходных сигналов прибора

30 Принцип неопределенности Найквиста Уравнение Найквиста для мощность шума Pt Pш

31 Нормированные формы представления результатов измерений

32 1. (8,334 ± 0,012) г; Р = 0, ,014 мм. Характеристики погрешностей и условия измерений по РД – 86, вариант 7 к. 3. (32,010…32,018) мм Р = 0,95. Измерение индикатором ИЧ 10 кл. точности 0 на стандартной стойке с настройкой по концевым мерам длины 3 кл. точности. Измерительное перемещение не более 0,1 мм; температурный режим измерений ± 2 оС ,6360 мм; Δн= – 0,0012 мм, Δв= + 0,0018 мм, Релей; Р = 0, ,75 м 3/с; σ (Δ) = 0,11 м 3/с, σ (Δс) = 0,18 м 3/с, равн. Условия измерений: температура среды 20 оС, кинематическая вязкость измеряемого объекта 1,5·10 –6 м 2/с. Примеры форм представления результатов измерений

35 Пример из Шишкин «Теоретическая метрология» –доработать

Видео:Лекция 1.1. Метрология, основные понятия и принципы | НанометрологияСкачать

Основной постулат метрологии

Видео:Неопределенность измерений - Uncertainty of measurementСкачать

Основной постулат метрологии

Процедура, которая сравнивает неизвестный размер с известным размером. Первое-второе выражение множественного или дробного отношения математически записывается как о ( 2) = x (2). Здесь соответствующая единица СИ функционирует как известный размер 2 при измерении физических величин. Информацию об этом можно найти либо в измерениях материала, либо в маркировке на считывателе, либо в калибровочных характеристиках прибора. При измерении сенсорных стимулов используется концепция единиц СИ, хранящихся в человеческой памяти, и измеренное значение измеряется с учетом (2).

При взвешивании сравнения иногда Создано с использованием стандартов, базовых или высококачественных идей: Кроме того, по сравнению с другими значениями значения являются физическими и нефизическими. В последнем случае эти значения выражаются, например, в точках. Уравнение (2), как и уравнение (3), называется уравнением измерения. И еще одно действие представляет собой процедуру сравнения, некоторые действия, которые на самом деле являются измеренными значениями. Основная особенность этой процедуры заключается в том, что при многократном измерении одного и того же значения определенного размера результат сравнения x, называемый критерием шкалы отношения, всегда отличается.

В некоторых случаях деление на равные части допуска, представленного линейной величиной, заменяется делением на части, где граница представлена О. Людмила Фирмаль

Этот, казалось бы, парадоксальный феномен отличает реальную деятельность от теоретических моделей. о Из уравнения (1). Огромный опыт фактических измерений, накопленный к настоящему времени, еще больше указывает на то, что в натуральных числах они совершенно разные. Теоретически, отношение двух размеров у должно быть четко определенным неслучайным числом. Фактически, сравнение этих размеров является результатом многих случайных и неслучайных ситуаций.

Это сделано ниже, но его точный расчет невозможен, поэтому результаты сравнения отличаются друг от друга, эта позиция, установленная практикой, сформулирована в форме аксиомы, Это можно назвать предпосылкой: эталоном является случайное число, поэтому значение измеренной величины существует, но не может быть определено. Первая часть этого утверждения является отражением материалистической концепции материаловедения, а вторая часть основана на решении, которое выявляет противоречие и обеспечивает основу для прогресса в области измерения. Из основной идеи измерения вы также можете видеть, что результат сравнения х неоднозначен.

Для обеспечения единообразия, сопоставимости, надежности, точности и объективности измерений в таких условиях принимаются дополнительные правовые меры и меры по измерению, связанные с получением, представлением и использованием результатов измерений. Все аспекты должны быть строго регламентированы. Это в некоторой степени объясняет существование законодательной метрологии, государственного надзора и ведомственного управления в отношении метрологических правил, требований и норм, соответствия государственным и ведомственным метрологическим службам.

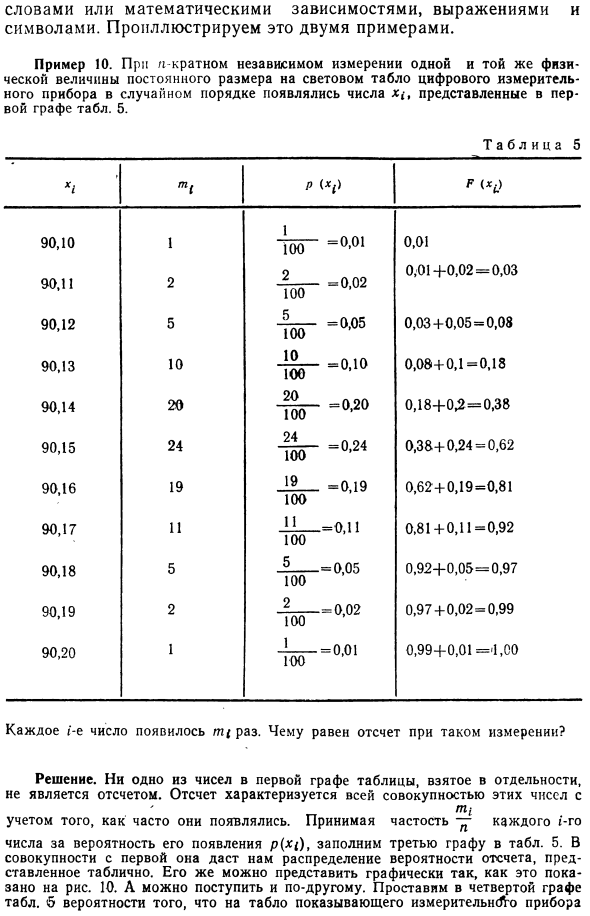
Многие трудности в измерении связаны с тем, что счет не может быть представлен одним числом. Могу только объяснить Слово или математическая зависимость, выражение, символ. Два примера иллюстрируют это. Пример 10. 11-е значение стоящего устройства находится в случайном столбце 1 таблицы. 5. На световой панели заказа цифрового счетчика отображалось числовое значение xb, где сначала отображаются несколько независимых измерений одинакового размера.

Таблица 5. 90.10 90.11 90.12 90.13 90.14 90.15 90.16 90.17 90.18 90.19 90.20 2 5 10 20 24 19 5 2 1 Loo 5 °> 01 T G — — = 0,05 100 * 9 -0,19 100 L- = o, 11 100 L = 0,05 100 два. — 0,02 100 -1 ^ — = 0,01 0,01 0,01 + 0,02 = 0,03 0,03 + 0,05 = 0,08 0,08 + 0,1 = 0,18 0,18 + 0,2 = 0,38 0,38 + 0,24 = 0,62 0,62 + 0,19 = 0,81 0,81 + 0,11 = 0,92 0,92 + 0,05 = 0, 97 0,97 + 0,02 = 0,99 0,99 + 0,01 = 4,00 Решения. Числа в первом столбце таблицы не взяты по отдельности, но не являются обратным отсчетом. Обратный отсчет характеризуется суммой этих чисел с учетом количества вхождений. Введите каждую частоту (i-е число как ее вероятность появления p (X ()) в третьем столбце таблицы 5.

Вместе с первым столбцом распределение вероятности считывания, отображаемое в таблице, составляет Однако можно действовать по-другому: в четвертом столбце таблицы 5 введите вероятность того, что инструмент появится на дисплее. Отображение первого числа следующих номера в сочетании с колонкой, которая по распределению опорного кадра получается. подсчитывать Появляется в первом столбце. в Измерительный инструмент метр Распределение вероятности p (x1) и функция распределения вероятности P (x1) являются исчерпывающим описанием ссылок на цифровые конструкции для всех конструкций. Пример 11.

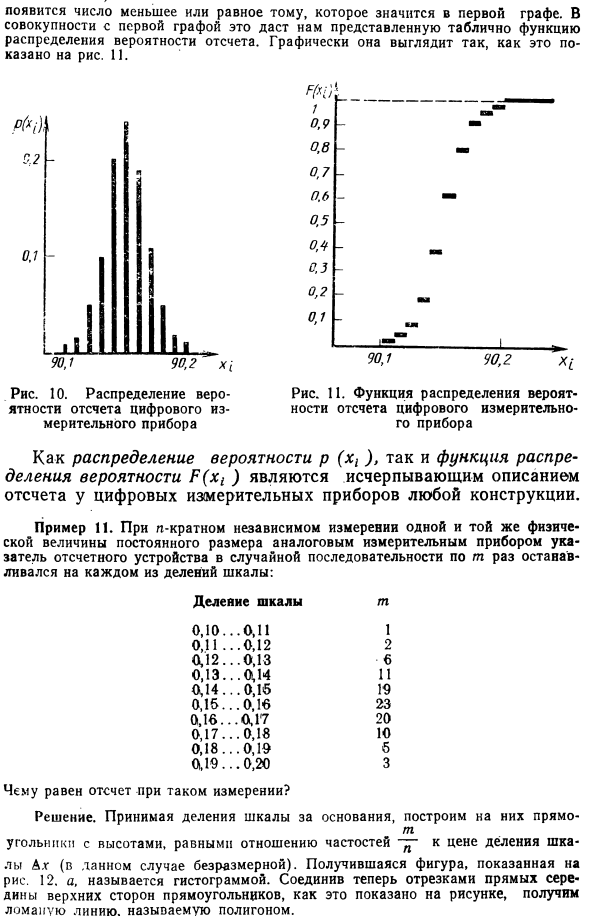
Когда аналоговое измерительное устройство выполняло независимое измерение одной и той же физической величины постоянного размера, указатель считывающего устройства произвольно останавливался m раз в каждом сегменте тика. градация 0,10 … 0,11 1 Ох и … 0,12 2 D12 … O.13 6 0,13 … 0,14 11 0,14 … 0,15 10 0,15 … 0,16 23 0,16 … 0,17 20 0,17 … 0,18 10 0,18 … 0,19 б 0,19 … 0,20 3 Какой отсчет для этого измерения Решения.

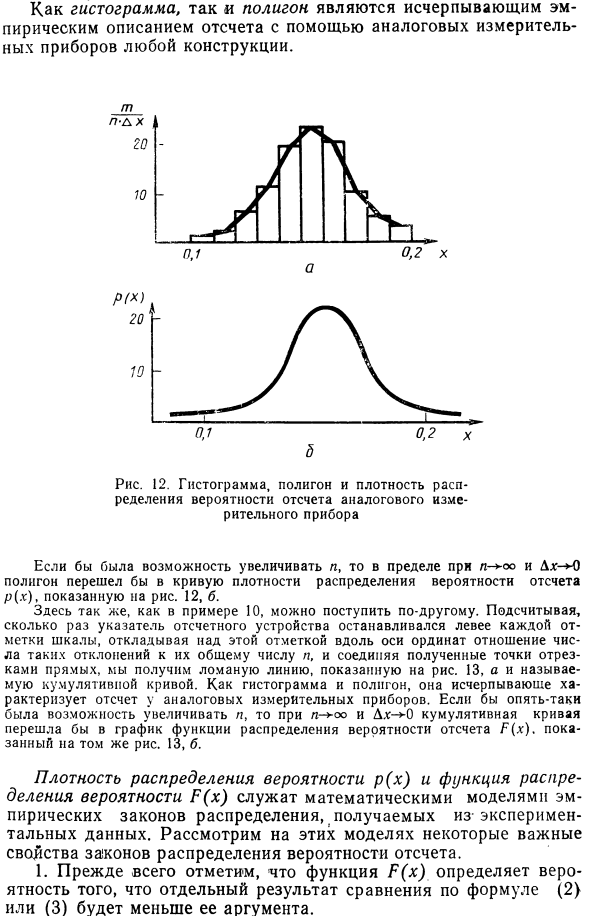
Взятие Квадратный масштаб деления топоров с высотой, равной соотношению частот (в данном случае безразмерно). Полученная диаграмма показана на рисунке. 12. а, называется гистограммой. Как показано на рисунке, когда прямая линия соединена в центре верхней стороны прямоугольника, получается ломаная линия, называемая многоугольником. И гистограммы, и полигоны являются исчерпывающими эмпирическими описаниями показаний с использованием произвольно разработанных аналоговых инструментов.

Рисунок 12. Гистограмма, полигон и плотность, определяющие вероятность чтения аналогового ритуального устройства Если л можно увеличить, в пределах у0 и Dx-М, многоугольники достигнет кривой распределения плотности вероятности опорной вероятности р (х), показанного на 12, б. Пример 10, один тип. подсчитывать Слева от каждой осени на этой ординате Общее количество точек отсечения Линия, пунктирная линия 13 на рисунке, телефон Эмулирует кривую. Комплексная характеристика показаний аналоговых приборов, таких как гистограммы и полигоны.

Опять же, если может быть увеличено, для — * x> и Dx — — 0 кумулятивная кривая является графиком функции распределения вероятностей, которая читает (x). Показано на той же фотографии. 13 б Плотность вероятности p (x) и функция распределения вероятности P (x) функционируют как математическая модель эмпирических правил распределения, полученных из экспериментальных данных. Для этих моделей рассмотрим некоторые важные характеристики закона распределения эталонных вероятностей. 1. Во-первых, обратите внимание, что функция P (x) определяет вероятность того, что результат отдельного сравнения из уравнения (2 или (3) будет меньше, чем его аргумент. 2.

Вероятность никогда не будет отрицательной, / (X)> 0. Чем больше х, тем больше вероятность того, что результат сравнения с использованием уравнения (2) или (3) не будет превышать это значение. То есть G (x) является неубывающей функцией. h (x1)> T (x1), истинно x1> X1. Когда x изменяется от -oo до + oo, P (x) изменяется от 0 до 1. 3. Результат индивидуального сравнения формулы (2) или (3 / вероятность P (x ) меньше, чем X1 и вероятность P (xg) меньше, чем X1. Следовательно, формула (2) или (3) Интервал xy x2 равен разности значений P (x). P (x1 x x,) — (X.) — (x1). Аналоговое измерительное устройство X И x2 может быть произвольно выбрано между собой. X is- * XrP (xr) -P (x ) 0.

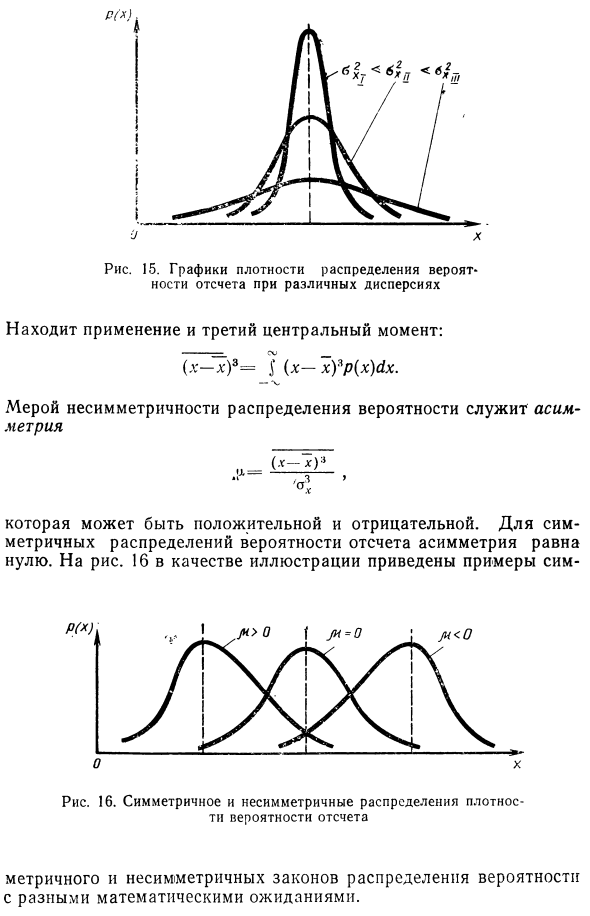
Таким образом, для аналоговых приборов вероятность того, что указатель считывающего устройства остановится в определенной точке шкалы, равна нулю. Следовательно, P x . X xr = P X x x2 = P x x x2 = P x1 x x2 , то есть экстремальные значения могут или не могут быть включены в интервал Есть. 4. Плотность вероятности p (x) связана с функцией распределения вероятности P (x) следующим соотношением: p (x) = P (xY Следовательно, p (x) также называется дифференциальной функцией распределения вероятностей. Аналогично, P (x) может быть получено путем интегрирования p (x) в соответствующих пределах. П (Хо) — /> (*) ** Геометрическая интерпретация этой операции показана на рисунке.

Микрометр имеет растровый преобразователь 1 и электронный блок 2 с выходом для передачи информации в систему управления. Людмила Фирмаль

Также называется интегральной функцией распределения вероятностей. Рисунок 14. Дифференциальная функция распределения вероятностей 5. P (x) — неубывающая функция, поэтому ее производная не может быть отрицательной. /> (X)> 0. 6. Результат сравнения по уравнению (2) или (3) находится в диапазоне x2; x2 , равен и ограничен График перпендикулярно Пей в функции р (х), горизонтальной оси и границы интервала (см. Рисунок 14): x x,) = р (х) с1х. 7. Увеличение интервала на неопределенный срок делает данное событие достоверным. Следовательно, площадь, ограниченная графиком функции p (x) и горизонтальной осью, равна 1. p (x) c1x = 1.

Написание ссылок с использованием законов распределения вероятностей является наиболее полным, но неудобным. Во многих случаях они ограничиваются приблизительным описанием закона распределения эталонных вероятностей с использованием их числовых свойств или моментов. Все они представляют средние значения, и когда значения, отсчитанные от начала координат, усредняются, момент называется начальным, а когда он центрирован от центра закона распределения, он называется моментом. Общие правила формирования начальных моментов: V = xG p (x) Lx, Где r — количество моментов.

Наиболее важной отправной точкой является первый средний * = ^ P (x) 0x. Это характеризует математическое ожидание в расчете на бесконечную итерацию процедуры сравнения в соответствии с уравнением (2) или (3). Возможно, будет удобнее обозначить это символом M (x). Характеристики математических ожиданий: 1) Неслучайным математическим ожиданием является именно это число: M (a) = a, где a = const1; 2) Постоянный коэффициент может быть извлечен из математического символа ожидания.

Математическое ожидание алгебраической суммы независимых случайных чисел равно алгебраической сумме математического ожидания: M (x + y — r) = M (x) 4-M (y) -M (g); 4) Математическое ожидание произведения независимых случайных чисел равно произведению этих математических ожиданий: M (x.r.g) = M (x) -M (p) .M (g); 5) математическое ожидание отклонения случайного числа от математического ожидания равно нулю: М х — М (х) = 0. Второй центральный момент служит мерой дисперсии результата сравнения согласно уравнению (2) или (3), близкому к среднему значению задания.

Общее правило формирования центрального момента записывается следующим образом: (X ^) = Uh

x) p (x) 0x, Из этого сразу видно, что начальный центральный момент равен нулю. x-x = (x-x) p (x) dx =; xp (x) ax-x p x) (1x = x-x 1 = 0. Второй центральный момент называется дисперсией и обозначен *. o = (^) ^ (x-

xUr (x) Ох. Может быть более удобно указывать дисперсию с символом O (x).

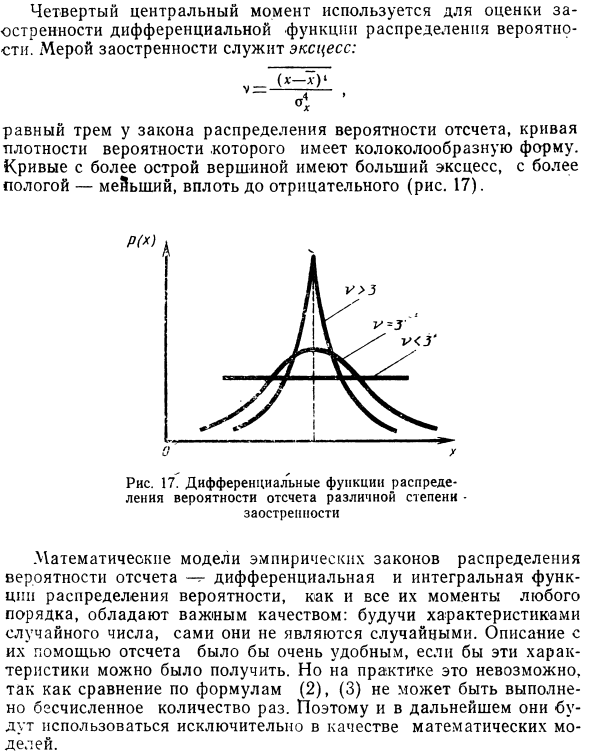
Дисперсионные характеристики: 1) Неслучайная дисперсия равна нулю: O (a) = 0, где a = const ; 2) Постоянный коэффициент может быть взят из символа отклонения, но он возводится в квадрат: O (ах) = а О (х); 3) Дисперсия алгебраической суммы независимых случайных чисел равна арифметической сумме этих дисперсий: O (x + y-r) = O (x) + E (y) + O (g); 4) Дисперсия случайного числа равна разнице между значением квадратного математического ожидания и значением квадратного математического ожидания: O (x) = M (x2) -M2 (x). минут Чем больше дисперсия, тем больше дисперсия результатов сравнения для x (2) и (3). Это хорошо видно на рисунке.

На рисунке 15 показана та же кривая плотности закона для распределения опорных вероятностей при различных дисперсиях. При измерении стандартное отклонение часто используется в качестве меры рассеяния. — + КИ. Третья центральная точка также находит применение. (X-7) 8 = (x-x) 3p (x) 0x. Мера асимметрии в распределении вероятностей — асимметрия Это может быть положительным или отрицательным. Для симметричного эталонного распределения вероятностей асимметрия равна нулю.

Вот пример из рисунка 16 Рисунок 16. Симметричное и асимметричное вычисление опорных вероятностей Метрический и асимметричный закон распределения вероятностей с различными математическими значениями ожидания. Четвертый центральный момент используется для оценки резкости дифференциальной функции распределения вероятностей. Мера резкости чрезмерна. Эквивалентно трем кривым плотности вероятности, которые являются законами эталонного распределения вероятностей.

Кривые с более острыми пиками больше и имеют более плоские минимумы, максимумы и максимумы и отрицательные значения (рис. 17). Рисунок 17 Дифференциальная функция распределения Он был остроконечный предмет Эвристическая математическая модель распределения эталонных вероятностей — дифференциальных и интегральных функций распределения вероятностей, а также всех моментов всех порядков, обладает важными свойствами: случайными характеристиками, а не случайными , Учитывая эти характеристики, объяснения со ссылками очень полезны. Однако на практике это невозможно, поскольку существует бесчисленное множество сравнений с использованием уравнений (2) и (3).

Поэтому в будущем По математике Они используются исключительно. Показывает одну и ту же кривую плотности закона распределения эталонных вероятностей при разных дисперсиях.