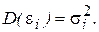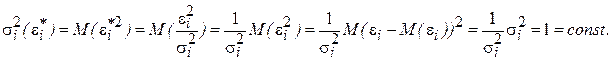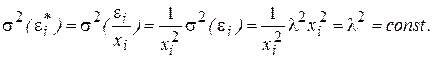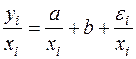Методы устранения гетероскедастичности остатков в уравнении регрессии (3 видео)

Устранение гетероскедастичности

В случае, когда присутствие гетероскедастичности установлено, возникает необходимость преобразования регрессионной модели с целью устранения данного нежелательного явления. Вид преобразования зависит от того, известны или нет дисперсии случайных отклонений

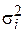
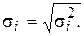
Предположим, что рассматриваемая модель гетероскедастична, и нам известны значения дисперсий остатков для каждого t-го наблюдения. При отсутствии автокорреляции это означает, что ковариационная матрица случайных отклонений V(e) = W — диагональная. В данном случае можно устранить гетероскедастичность, разделив каждое значение зависимой и объясняющих переменных на соответствующее стандартное отклонение Нормируя («взвешивая») переменные по σ_i, мы стремимся получить более точные оценки. В этом заключается суть так называемого взвешенного метода наименьших квадратов (ВМНК).

Для простоты изложения опишем ВМНК на примере парной регрессии:

Разделим каждый член модели (5.7) на известное σ_i:

(5.8)

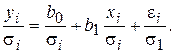
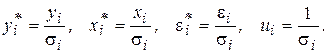
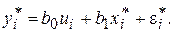
Введем обозначения Тогда уравнение модели (5.7) примет вид:

(5.9)

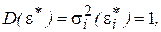
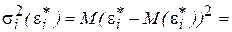
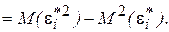
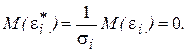
Полученное уравнение представляет собой регрессию без свободного члена, но с дополнительной объясняющей переменной U и с преобразованным случайным отклонением e*. Для преобразованной модели (5.9) дисперсия остатков т. е. имеет место гомоскедастичность. Действительно, можно записать Так как, согласно первой предпосылке МНК, математическое ожидание М(e_i) = 0, то Следовательно,

Таким образом, ковариационная матрица W в выражении (5.1) становится единичной, а сама преобразованная модель (5.9) – классической, к которой применим «обычный» МНК. Другими словами, в данном случае обобщенным методом наименьших квадратов для модели с гетероскедастичностью является взвешенный метод наименьших квадратов (ВМНК). «Взвешивая» каждый остаток 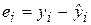с помощью коэффициента 1/σ_i, мы добиваемся равномерного вклада остатков в общую дисперсию и, в конечном счете, получения эффективных оценок параметров модели.

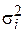
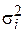
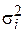
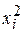
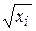
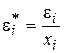
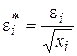
Рассмотренная выше процедура применения ВМНК предполагает, что фактические значения дисперсий нам известны. Как уже было отмечено, такое предположение реализуется крайне редко. Для применения ВМНК на практике необходимо сделать некоторые достаточно реалистические предположения о значениях . Например, может оказаться целесообразным предположить, что дисперсии остатков e_i пропорциональны значениям (стандартное отклонение остатков пропорционально независимой переменной) или значениям х_i. Тогда необходимым преобразованием будет деление уравнения регрессии (5.7) на х_i или соответственно, что позволит нам получить «преобразованные» случайные отклонения и , для которых выполняется условие гомоскедастичности. Например, определим дисперсию случайного члена для случая пропорциональности стандартного отклонения значениям независимой переменной (σ_i = σ(e_i) = lх_i, где l — коэффициент пропорциональности). В силу выполнимости предпосылки МНК имеем:

Несложно показать, что для отклонений 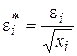также выполняется условие гомоскедастичности. Таким образом, для оценки преобразованных регрессий возможно применение МНК.

Рассматривая проведенные выше преобразования и их результаты, следует отметить, что применение обобщенного метода наименьших квадратов для моделей с гетероскедастичностью остатков заключается в минимизации суммы взвешенных квадратов отклонений выборочных данных от их оценок.

Видео:Часть 2. Множественная регрессия в Microsoft Excel. Автокорреляция, гетероскедастичность.Скачать

Автокорреляция

При анализе временных рядов часто приходится учитывать статистическую зависимость (коррелированность) наблюдений в разные моменты времени. Следовательно, в данном случае для регрессионных моделей Cov(e_i, e_j) ¹ 0, i ¹ j, т. е. третья предпосылка Гаусса-Маркова о некоррелированности остатков не выполняется. Такие регрессионные зависимости называются моделями с автокорреляцией (сериальной корреляцией) остатков. Для обобщенной линейной регрессионной модели с автокорреляцией ковариационная матрица случайных отклонений W не может быть диагональной.

Последствия автокорреляции остатков во многом сходны с последствиями гетероскедастичности (см. раздел 5.2). Среди них особенно следует выделить ухудшение прогнозных качеств моделей временных рядов.

Поскольку автокорреляция рассматривается в регрессионном анализе при использовании данных временных рядов, в дальнейших выкладках вместо символа i порядкового номера наблюдения будем использовать символ t отражающий момент наблюдения во времени (t = 1, 2, …, n). В экономических задачах более часто встречается так называемая положительная автокорреляция (Cov(e_t _— ₁, e_t) > 0 для соседних отклонений), нежели отрицательная автокорреляция (Cov(e_t _— ₁, e_t)

Дата добавления: 2016-06-02 ; просмотров: 2636 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Сравнение оценок при гетероскедастичностиСкачать

Устранение гетероскедастичности. Метод взвешенных наименьших квадратов.

Одной из ключевых предпосылок МНК является условие постоянства дисперсий случайных отклонений для любых наблюдений. Выполнимость данной предпосылки называетсягомоскедастичностью; невыполнимость данной предпосылки называется гетероскедастичностью.

В качестве примера реальной гетероскедастичности можно сказать, что люди с большим доходом не только тратят в среднем больше, чем люди с меньшим доходом, но и разброс в их потреблении также больше, поскольку они имеют больше простора для распределения дохода.

При гетероскедастичности последствия применения МНК будут следующими:

1. Оценки параметров останутся по-прежнему несмещенными и линейными.

Видео:Робастные стандартные ошибки и обнаружение гетероскедастичностиСкачать

2. Оценки не будут эффективными, т.е. не будут иметь наименьшую дисперсию по сравнению с другими оценками данного параметра. Они не будут даже асимптотически эффективными. Увеличение дисперсии оценок снижает вероятность получения максимально точных оценок.

3. Дисперсии оценок параметров будут рассчитываться со смещением.

4. Все выводы, получаемые на основе соответствующих t – и F – статистик, а также интервальные оценки будут ненадежными. Вполне вероятно, что стандартные ошибки коэффициентов будут занижены, а t – статистики завышены. Это может привести к признанию статистически значимыми коэффициентов, которые таковыми на самом деле не являются.

При установлении гетероскедастичности возникает необходимость преобразования модели с целью устранения данного недостатка. Вид преобразования зависит от того, известны или нет дисперсии отклонений .

В случае, если дисперсии отклонений известны для каждого наблюдения, применяется методвзвешенных наименьших квадратов(ВНК). Гетероскедастичность устраняется, если разделить каждое наблюдаемое значение на соответствующее ему значение дисперсии.

Рассмотрим для простоты ВНК на примере парной регрессии:

(57)

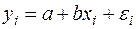
Разделим обе части (57) на известное :

(58)

Видео:Что такое Гомоскедастичность и ГетероскедастичностьСкачать

Сделаем замены переменных:

(59)

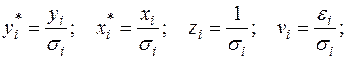
получим уравнение регрессии без свободного члена, но с двумя факторами и с преобразованным отклонением:

(60)

Можно показать, что для v_i выполняется условие гомоскедастичности. Поэтому для модели (60) выполняются все предпосылки МНК, и оценки, полученные по МНК, будут наилучшими линейными несмещенными оценками.

Таким образом, наблюдения с наименьшими дисперсиями получают наибольшие «веса», а наблюдения с наибольшими дисперсиями – наименьшие «веса». Поэтому наблюдения с меньшими дисперсиями отклонений будут более значимыми при оценке параметров регрессии, чем наблюдения с большими дисперсиями. При этом повышается вероятность получения более точных оценок.

Полученные по МНК оценки параметров модели (60) можно использовать в первоначальной модели (57).

Для применения ВНК необходимо знать фактические значения дисперсий отклонений . На практике такие значения известны крайне редко. Поэтому, чтобы применить ВНК, необходимо сделать реалистические предположения о значениях . Чаще всего предполагается, что дисперсии отклонений пропорциональны или значениям x_i, или значениям .

Видео:Множественная регрессия в Excel и мультиколлинеарностьСкачать

Если предположить, что дисперсии пропорциональны значениям фактора x, т.е.

(61)

тогда уравнение (57) преобразуется делением его левой и правой частей на :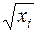

(62)

Здесь для случайных отклонений выполняется условие гомоскедастичности. Следовательно, для регрессии (62) применим обычный МНК. Следует отметить, что регрессия (62) не имеет свободного члена, но зависит от двух факторов. Оценив для (62) по МНК коэффициенты а и b, возвращаемся к исходному уравнению регрессии.

Если в уравнении регрессии присутствует несколько объясняющих переменных, вместо конкретной переменной x_j используется исходное уравнение множественной регрессии

т.е. фактически линейная комбинация факторов. В этом случае получают следующую регрессию:

(63)

Если предположить, что дисперсии пропорциональны , то соответствующим преобразованием будет деление уравнения регрессии (57) на x_i:

или, если переобозначить остатки как :

(64)

Здесь для отклонений v_i также выполняется условие гомоскедастичности. Применяя обычный МНК к регрессии (64) в преобразованных переменных

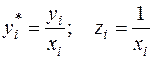
получим оценки параметров, после чего возвращаемся к исходному уравнению (57). Отметим, что в регрессии (64) по сравнению с исходным уравнением параметры поменялись ролями: свободный член а стал коэффициентом, а коэффициент b – свободным членом.

Видео:Парная регрессия: линейная зависимостьСкачать