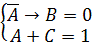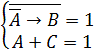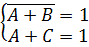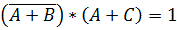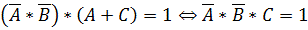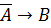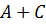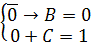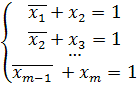статья по информатике и икт (10 класс) по теме
Методы решения систем логических уравнений при подготовке к ЕГЭ (задание В15)
Видео:14 Метод половинного деления Ручной счет Численные методы решения нелинейного уравненияСкачать
Скачать:
| Вложение | Размер |
|---|---|
| Методы решения систем логических уравнений | 296.5 КБ |
Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать
Предварительный просмотр:
Методы решения систем логических уравнений
Решить систему логических уравнений можно, например, с помощью таблицы истинности (если количество переменных не слишком велико) или с помощью дерева решений, предварительно упростив каждое уравнение.
1. Метод замены переменных.
Ввод новых переменных позволяет упростить систему уравнений, сократив количество неизвестных. Новые переменные должны быть независимыми друг от друга . После решения упрощенной системы надо снова вернуться к первоначальным переменным.
Рассмотрим применение этого метода на конкретном примере.
Пример. Сколько различных решений имеет система уравнений
((X1 ≡ X2) ∧ (X3 ≡ X4)) ∨ (¬(X1 ≡ X2) ∧ ¬(X3 ≡ X4)) = 0
((X3 ≡ X4) ∧ (X5 ≡ X6)) ∨ (¬(X3 ≡ X4) ∧ ¬(X5 ≡ X6)) = 0
((X5 ≡ X6) ∧ (X7 ≡ X8)) ∨ (¬(X5 ≡ X6) ∧ ¬(X7 ≡ X8)) = 0
((X7 ≡ X8) ∧ (X9 ≡ X10)) ∨ (¬(X7 ≡ X8) ∧ ¬(X9 ≡ X10)) = 0
где x1, x2, …, x10 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.
Введем новые переменные: А=(X1 ≡ X2); В=(X3 ≡ X4); С=(X5 ≡ X6); D=(X7 ≡ X8); E=(X9 ≡ X10).
(Внимание! Каждая их переменных x1, x2, …, x10 должна входить только в одну из новых переменных А,В,С,D,Е, т.е. новые переменные независимы друг от друга).
Тогда система уравнений будет выглядеть так:
Построим дерево решений полученной системы:
Рассмотрим уравнение А=0, т.е. (X1 ≡ X2)=0. Оно имеет 2 корня:
Из этой же таблицы видно, что уравнение А=1 тоже имеет 2 корня. Расставим кол-во корней на дереве решений:
Чтобы найти количество решений одной ветви, надо перемножить количества решений на каждом ее уровне. Левая ветвь имеет 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2=32 решения; правая ветвь имеет тоже 32 решения. Т.е. вся система имеет 32+32=64 решения.
2. Метод рассуждений.
Сложность решения систем логических уравнений состоит в громоздкости полного дерева решений. Метод рассуждений позволяет не строить все дерево полностью, но понять при этом, сколько оно будет иметь ветвей. Рассмотрим этот метод на конкретных примерах.
Пример 1. Сколько существует различных наборов значений логических переменных x1, x2, x3, x4, x5, y1, y2, y3, y4, y5, которые удовлетворяют всем перечисленным ниже условиям?
(x1→x2) / (x2→x3) / (x3→x4) / (x4→x5 ) = 1
(y1→y2) / (y2→y3) / (y3→y4) / (y4→y5 ) = 1
В ответе не нужно перечислять все различные наборы значений переменных x1, x2, x3, x4, x5, y1, y2, y3, y4, y5, при которых выполнена данная система равенств. В качестве ответа Вам нужно указать количество таких наборов.
Первое и второе уравнения содержат независимые переменные, которые связаны третьим условием. Построим дерево решений первого и второго уравнений.
Чтобы представить дерево решений системы из первого и второго уравнений, надо каждую ветвь первого дерева продолжить деревом для переменных у . Построенное таким образом дерево будет содержать 36 ветвей. Некоторые из этих ветвей не удовлетворяют третьему уравнению системы. Отметим на первом дереве количество ветвей дерева «у» , которые удовлетворяют третьему уравнению:
Поясним: для выполнения третьего условия при х1=0 должно быть у1=1, т.е все ветви дерева «х» , где х1=0 можно продолжить только одной ветвью из дерева «у» . И только для одной ветви дерева «х» (правой) подходят все ветви дерева «у». Таким образом, полное дерево всей системы содержит 11 ветвей. Каждая ветвь представляет собой одно решение исходной системы уравнений. Значит, вся система имеет 11 решений.
Пример 2. Сколько различных решений имеет система уравнений
(X1 ≡ X2) ∨ (X1 ∧ X10) ∨ (¬X1 ∧ ¬ X10)= 1
(X2 ≡ X3) ∨ (X2 ∧ X10) ∨ (¬X2 ∧ ¬ X10)= 1.
(X9 ≡ X10) ∨ (X9 ∧ X10) ∨ (¬X9 ∧ ¬ X10)= 1
где x1, x2, …, x10 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.
Решение : Упростим систему. Построим таблицу истинности части первого уравнения:
Видео:Сколько решений имеет лог. уравнение (!(A *B) + C) IMP (!A * !B + D) = 1. Информатика, ЕГЭ, логикаСкачать
Методы решения уравнений в информатике
Можно выделить различные способы решения систем логических уравнений. Это сведение к одному уравнению, построение таблицы истинности и декомпозиция.
Задача: Решить систему логических уравнений:
Рассмотрим метод сведения к одному уравнению. Данный метод предполагает преобразование логических уравнений, таким образом, чтобы правые их части были равны истинностному значению (то есть 1). Для этого применяют операцию логического отрицания. Затем, если в уравнениях есть сложные логические операции, заменяем их базовыми: «И», «ИЛИ», «НЕ». Следующим шагом объединяем уравнения в одно, равносильное системе, с помощью логической операции «И». После этого, следует сделать преобразования полученного уравнения на основе законов алгебры логики и получить конкретное решение системы.
Решение 1: Применяем инверсию к обеим частям первого уравнения:
Представим импликацию через базовые операции «ИЛИ», «НЕ»:
Поскольку левые части уравнений равны 1, можно объединить их с помощью операции “И” в одно уравнение, равносильное исходной системе:
Раскрываем первую скобку по закону де Моргана и преобразовываем полученный результат:
Полученное уравнение, имеет одно решение: A =0, B=0 и C=1.
Следующий способ – построение таблиц истинности. Поскольку логические величины имеют только два значения, можно просто перебрать все варианты и найти среди них те, при которых выполняется данная система уравнений. То есть, мы строим одну общую таблицу истинности для всех уравнений системы и находим строку с нужными значениями.
Решение 2: Составим таблицу истинности для системы:
Полужирным выделена строчка, для которой выполняются условия задачи. Таким образом, A=0, B=0 и C=1.
Способ декомпозиции. Идея состоит в том, чтобы зафиксировать значение одной из переменных (положить ее равной 0 или 1) и за счет этого упростить уравнения. Затем можно зафиксировать значение второй переменной и т.д.
Решение 3: Пусть A = 0, тогда:
Из первого уравнения получаем B =0, а из второго – С=1. Решение системы: A = 0, B = 0 и C = 1.
В ЕГЭ по информатике очень часто требуется определить количество решений системы логических уравнений, без нахождения самих решений, для этого тоже существуют определенные методы. Основной способ нахождения количества решений системы логических уравнений – замена переменных . Сначала необходимо максимально упростить каждое из уравнений на основе законов алгебры логики, а затем заменить сложные части уравнений новыми переменными и определить количество решений новой системы. Далее вернуться к замене и определить для нее количество решений.
Задача: Сколько решений имеет уравнение ( A → B ) + ( C → D ) = 1? Где A, B, C, D – логические переменные.
Решение: Введем новые переменные: X = A → B и Y = C → D . С учетом новых переменных уравнение запишется в виде: X + Y = 1.
Дизъюнкция верна в трех случаях: (0;1), (1;0) и (1;1), при этом X и Y является импликацией, то есть является истинной в трех случаях и ложной – в одном. Поэтому случай (0;1) будет соответствовать трем возможным сочетаниям параметров. Случай (1;1) – будет соответствовать девяти возможным сочетаниям параметров исходного уравнения. Значит, всего возможных решений данного уравнения 3+9=15.
Следующий способ определения количества решений системы логических уравнений – бинарное дерево. Рассмотрим данный метод на примере.
Задача: Сколько различных решений имеет система логических уравнений:
Приведенная система уравнений равносильна уравнению:
Предположим, что x 1 – истинно, тогда из первого уравнения получаем, что x 2 также истинно, из второго — x 3=1, и так далее до xm = 1. Значит набор (1; 1; …; 1) из m единиц является решением системы. Пусть теперь x 1=0, тогда из первого уравнения имеем x 2 =0 или x 2 =1.
Когда x 2 истинно получаем, что остальные переменные также истинны, то есть набор (0; 1; …; 1) является решением системы. При x 2=0 получаем, что x 3=0 или x 3=, и так далее. Продолжая до последней переменной, получаем, что решениями уравнения являются следующие наборы переменных ( m +1 решение, в каждом решении по m значений переменных):
Такой подход хорошо иллюстрируется с помощью построения бинарного дерева. Количество возможных решений – количество различных ветвей построенного дерева. Легко заметить, что оно равно m +1.
Видео:10 Численные методы решения нелинейных уравненийСкачать
Решение систем логических уравнений
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Описание презентации по отдельным слайдам:
14.06.2005 (формальная) Математическая логика Часть 5. Решение систем логических уравнений
Системы логических уравнений (ЕГЭ-2011) Три типа задач: I тип — В уравнениях используется операции дизъюнкции (конъюнкции), одна переменная входит в 2 уравнения. II тип — В уравнениях используется операции дизъюнкции (конъюнкции), сложные переменные представлены тождеством, одна сложная переменная входит в 2 уравнения. III тип — В уравнениях используется операции дизъюнкции (конъюнкции), сложные переменные, которые могут быть упрощены путем введения независимых новых переменных и применения законов логических преобразований. IV тип — В уравнениях используется операции дизъюнкции (конъюнкции), сложные переменные, которые не могут быть упрощены путем введения независимых новых переменных. V тип – Одна переменная входит в одно слагаемое во всех уравнениях VI, VII тип – Одна переменная входит во все слагаемые в уравнении одним из наиболее известных проектов создания компьютеров пятого поколения предполагается использование логических исчислений в качестве основной системы программирования. Поэтому специалисты, работающие в различных областях информатики, проявляют все большее внимание и интерес к математической логике. Проникновение методов математической логики в информатику уже привело к новым результатам, имеющим первостепенное практическое значение. В частности, к созданию нового языка программирования ПРОЛОГ — языка, принципиально отличающегося от всех созданных ранее.
I тип Сколько различных решений имеет система уравнений ¬X1 X2 = 1 ¬X2 X3 = 1 . ¬X9 X10 = 1 где x1, x2, …, x10 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов. ¬X1 X2 = 1 Ответ: 11 вариантов решений Типы уравнений I Решаем второе уравнение http://krolyakov.narod.ru ¬X1 = 0 X2 = 1 ¬X1 = 1 X2 = 0 ¬X1 = 1 X2 = 1 X1 = 1 X2 = 1 X1 = 0 X2 = 0 X1 = 0 X2 = 1 X2 = 1 X3 = 1 X2 = 0 X3 = 0 X2 = 0 X3 = 1 X2 X1 0 0 1 0 1 1 X3 X2 X1 0 0 0 1 0 0 1 1 0 1 1 1 Кол-во уравнений Кол-вопеременных Кол-во вариантов решений 1 2 3 2 3 4 3 4 5 Решаем по очереди уравнения и ищем закономерности накопления вариантов решений:
Сколько различных решений имеет система уравнений X1 ¬ X2 = 1 X2 ¬ X3 = 1 . X9 ¬ X10 = 1 где x1, x2, …, x10 – логические переменные? Решаем самостоятельно Первое уравнение: X1 ¬ X2 = 1 Второе уравнение: X2 ¬ X3 = 1 Ответ: 11 вариантов решений http://krolyakov.narod.ru X1 = 0 ¬ X2 = 1 X1 = 1 ¬ X2 = 0 X1 = 1 ¬ X2 = 1 X1 = 0 X2 = 0 X1 = 1 X2 = 1 X1 = 1 X2 = 0 X2 = 0 X3 = 0 X2 = 1 X3 = 1 X2 = 1 X3 = 0 X2 X1 0 0 0 1 1 1 X3 X2 X1 0 0 0 0 0 1 0 1 1 1 1 1 Кол-вопеременных Кол-во вариантов решений 2 3 3 4 4 5
Сколько различных решений имеет система уравнений ¬X1 X2 = 0 ¬X2 X3 = 0 . ¬X9 X10 = 0 где x1, x2, …, x10 – логические переменные? Сколько различных решений имеет система уравнений ¬X1 X2 = 0 ¬X2 X3 = 0 . ¬X9 X10 = 0 где x1, x2, …, x10 – логические переменные? Сколько различных решений имеет система уравнений ¬X1 X2 = 1 ¬X2 X3 = 1 . ¬X9 X10 = 1 где x1, x2, …, x10 – логические переменные? Нет решения I 11 вариантов Нет решения Решаем по очереди уравнения и ищем закономерности накопления вариантов решений:
Вывод: Система уравнений типа ¬X1 X2 = 1, где используются операции дизъюнкции и одна переменная входит в 2 уравнения, имеют решение только в случае, когда дизъюнкция двух переменных равна 1. Кол-во вариантов решений = кол-во уравнений + 2, или Кол-во вариантов решений = кол-во переменных + 1. I
Задача 1. Следующие два высказывания истинны: Неверно, что если корабль А вышел в море, то корабль С – нет. В море вышел корабль В или корабль С, но не оба вместе. Какие корабли вышли в море. А= «корабль А вышел в море» В= «корабль В вышел в море» С= «корабль С вышел в море» А→ ¬ С = 0 А В = 1 Последовательное решение уравнений: А В = 1 А = 1 В = 0 А = 0 В = 1 А→ ¬ С = 0 А = 1 ¬ С = 0 А = 1 С = 1 А = 1 В = 0 С=1 Ответ:
II тип Сколько различных решений имеет система уравнений ¬(X1 X2) (X3 X4) = 1 ¬(X3 X4) (X5 X6) = 1 ¬(X5 X6) (X7 X8) = 1 ¬(X7 X8) (X9 X10) = 1 где x1, x2, …, x10 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов. Введем обозначение сложных переменных: Y1 = (X1 X2) Y2= (X3 X4) Y3 = (X5 X6) Y4 = (X7 X8) Y5 = (X9 X10) Запишем систему уравнений: ¬Y1 Y2 = 1 ¬Y2 Y3 = 1 ¬Y3 Y4 = 1 ¬Y4 Y5 = 1 Cистема имеет 6 вариантов решений. Переменные Y — независимые II http://krolyakov.narod.ru Y5 Y4 Y3 Y2 Y1 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 1 1 1 0 0 1 1 1 1 0 1 1 1 1 1
Найдем варианты решений для исходных переменных Кол-во комбинаций для одного варианта решений: N=25=32 Всего решений: 32*6=192 Алгоритм 1. Ввести обозначения для сложных переменных. 2. Записать систему для новых переменных. 3. Найти количество вариантов решений для системы с новыми переменными (m). 4. Определить число состояний (k) исходных переменных для одного варианта решения. 5. Определить число комбинаций (N) с учетом всего количества введенных переменных (n): N=kn 6. Определить итоговое количество вариантов решения системы: N*m II http://krolyakov.narod.ru Y1 = 0; Y1 = 1; X1 =1; X2=0; X1 =0; X2=1; X1 =0; X2=0; X1 =1; X2=1; X1 X2=0; X1 X2=1;
III. Сколько различных решений имеет система уравнений (X1 X2) (¬X1 ¬X2) (¬X3 X4) (X3 ¬X4) = 1 (X3 X4) (¬X3 ¬X4) (¬X5 X6) (X5 ¬X6) = 1 (X5 X6) (¬X5 ¬X6) (¬X7 X8) (X7 ¬X8) = 1 (X7 X8) (¬X7 ¬X8) (¬X9 X10) (X9 ¬X10) = 1 где x1, x2, …, x10 – логические переменные? Используется закон замены эквивалентности: A B = (A B) (¬ A ¬B) и замены инверсии эквивалентности: ¬ (A B) = ¬((A B) (¬ A ¬B)) = ¬(A B) ¬(¬ A ¬B) = (¬ A ¬ B) (A B) = ¬ A A ¬ A B A ¬ B ¬ B B = (¬ A B) (A ¬ B ) III (X1 X2) ¬ (X3 X4) =1 (X3 X4) ¬ (X5 X6) =1 (X5 X6) ¬ (X7 X8) =1 (X7 X8) ¬ (X9 X10) =1 Упростим уравнения: Решить самостоятельно. Проверка http://krolyakov.narod.ru
Замена эквивалентности Закон замены эквивалентности: A B = (A B) (¬ A ¬B) Замена инверсии эквивалентности: ¬ (A B) = ¬((A B) (¬ A ¬B)) = ¬(A B) ¬(¬ A ¬B) = (¬ A ¬ B) (A B) = ¬ A A ¬ A B A ¬ B ¬ B B = (¬ A B) (A ¬ B )
Введем обозначение сложных переменных: Y1 = (X1 X2) Y2= (X3 X4) Y3 = (X5 X6) Y4 = (X7 X8) Y5 = (X9 X10) Запишем систему уравнений: Y1 ¬Y2 = 1 Y2 ¬Y3 = 1 Y3 ¬Y4 = 1 Y4 ¬Y5 = 1 Cистема имеет 6 вариантов решений. III Найдем варианты решений для исходных переменных N=25=32 Всего решений: 32*6=192 http://krolyakov.narod.ru Y1 = 0; Y1 = 1; X1 X2=0; X1 X2=1; X1 =1; X2=0; X1 =0; X2=1; X1 =0; X2=0; X1 =1; X2=1; Y5 Y4 Y3 Y2 Y1 0 0 0 0 0 0 0 0 0 1 0 0 0 1 1 0 0 1 1 1 0 1 1 1 1 1 1 1 1 1
Сколько различных решений имеет система уравнений ((X1 X2) (X3 X4)) (¬(X1 X2) ¬(X3 X4)) = 1 ((X3 X4) (X5 X6)) (¬(X3 X4) ¬(X5 X6)) = 1 ((X5 X6) (X7 X8)) (¬(X5 X6) ¬(X7 X8)) = 1 ((X7 X8) (X9 X10)) (¬(X7 X8) ¬(X9 X10)) = 1 где x1, x2, …, x10 – логические переменные? IV Алгоритм решения: Вводим обозначения сложных высказываний и переписываем уравнения. Упрощаем уравнения, используя замену эквивалентности и инверсии эквивалентности. Определяем количество вариантов решения для веденных переменных. Определяем количество комбинаций исходных переменных для одного варианта. Определяем итоговое количество вариантов решения Решаем самостоятельно http://krolyakov.narod.ru
Введем обозначение сложных переменных: Y1 = (X1 X2) Y2= (X3 X4) Y3 = (X5 X6) Y4 = (X7 X8) Y5 = (X9 X10) Запишем систему уравнений: (Y1 Y2) (¬ Y1 ¬ Y2) = 1 (Y2 Y3) (¬ Y2 ¬ Y3) = 1 (Y3 Y4) (¬ Y3 ¬ Y4) = 1 (Y4 Y5) (¬ Y4 ¬ Y5) = 1 Cистема имеет 2 варианта решения. IV Упростим уравнения: Y1 Y2 = 1 Y2 Y3 = 1 Y3 Y4 = 1 Y4 Y5 = 1 Кол-во комбинаций для одного варианта решений: N=25=32 Всего решений: 32*2=64 http://krolyakov.narod.ru Y5 Y4 Y3 Y2 Y1 0 0 0 0 0 1 1 1 1 1
Сколько различных решений имеет система уравнений (X2 X1) (X2 X3) (¬X2 ¬ X3)= 1 (X3 X1) (X3 X4) (¬X3 ¬ X4)= 1 . (X9 X1) (X9 X10) (¬X9 ¬ X10)= 1 (X10 X1) = 0 где x1, x2, …, x10 – логические переменные? V Используется закон замены эквивалентности: (X2 X1) (X2 X3) = 1 (X3 X1) (X3 X4) = 1 . (X9 X1) (X9 X10)= 1 (X10 X1) = 0 http://krolyakov.narod.ru Применить замену переменных нельзя, так как не получится независимых переменных. Решаем табличным способом по уравнению.
V (X2 X1) (X2 X3) = 1 Решаем второе уравнение: (X3 X1) (X3 X4) = 1 Решаем первое уравнение: X2 X1=0 X2 X3=1 X2 X1=1 X2 X3=0 X2 X1=1 X2 X3=1 X1=0 X2 =1 X3=1 X1=1 X2 =0 X3=0 X1=1 X3 =1 X4=0 X1=0 X2 =0 X3=1 X1=1 X2 =1 X3=1 X1=0 X2 =0 X3=0 X3 X1=0 X3 X4=1 X3 X1=1 X3 X4=0 X3 X1=1 X3 X4=1 X1=0 X3 =1 X4=1 X1=1 X3 =0 X4=0 X1=1 X2 =1 X3=0 X1=0 X3 =0 X4=1 X1=1 X3 =1 X4=1 X1=0 X3 =0 X4=0 X1 X3 X2 0 0 0 0 1 0 1 0 0 0 1 1 1 0 1 1 1 1 X1 X4 X3 X2 0 0 0 0 0 1 0 0 0 1 1 0 1 0 0 0 0 1 1 1 1 0 0 1 1 1 1 1 1 0 1 1 Кол-вопере-менных Кол-во вариантов решений 3 6 4 8 5 10 6 12 7 14 8 16 9 18 10 20
V (X10 X1) = 0 X10 X1 Подключаем последнее уравнение: Ответ: Кол-во решений = 20-2=18 http://krolyakov.narod.ru X1 X4 X3 X2 0 0 0 0 0 1 0 0 0 1 1 0 1 0 0 0 0 1 1 1 1 0 0 1 1 1 1 1 1 0 1 1
VI. Сколько различных решений имеет система уравнений (X1 X2) (¬X1 ¬X2) (X1 X3) = 1 (X2 X3) (¬X2 ¬X3) (X2 X4) = 1 . (X8 X9) (¬X8 ¬X9) (X8 X10) = 1 где x1, x2, …, x10 – логические переменные? VI Решаем самостоятельно Применим закон замены эквивалентности: (X1 X2)(X1 X3)=1 (X2 X3)(X2 X4)=1 . (X8 X9)(X8 X10)=1 http://krolyakov.narod.ru Независимые переменные ввести нельзя, решаем по уравнению
Решаем первое уравнение: (X1 X2)(X1 X3)=1 Решаем второе уравнение: (X2 X3)(X2 X4)=1 VI http://krolyakov.narod.ru X1 X2=0 X1 X3=1 X1=0 X2 =1 X3=0 X1=1 X2 =0 X3=1 X1=0 X2 =0 X3=1 X1=1 X2 =1 X3=1 X1=0 X2 =0 X3=0 X1=1 X2 =1 X3=0 X1 X2=1 X1 X3=0 X1 X2=1 X1 X3=1 X2 X3=0 X2 X4=1 X2 X3=1 X2 X4=0 X2 X3=1 X2 X4=1 X2=0 X3 =1 X4=0 X2=1 X3 =0 X4=1 X2=0 X3 =0 X4=1 X2=1 X3 =1 X4=1 X2=0 X3 =0 X4=0 X2=1 X3 =1 X4=0 X3 X2 X1 0 0 0 1 0 0 0 1 0 1 0 1 0 1 1 1 1 1 X4 X3 X2 X1 0 0 0 0 1 0 0 0 1 0 1 0 1 0 1 1 1 1 1 1 X4 X3 X2 X1 0 0 0 0 1 0 0 0 0 1 0 0 1 0 1 0 0 1 0 1 1 0 1 1 0 1 1 1 1 1 1 1
Ответ: 20 вариантов VI http://krolyakov.narod.ru X3 X2 X1 0 0 0 1 0 0 0 1 0 1 0 1 0 1 1 1 1 1 X4 X3 X2 X1 0 0 0 0 1 0 0 0 0 1 0 0 1 0 1 0 0 1 0 1 1 0 1 1 0 1 1 1 1 1 1 1 Кол-вопеременных Кол-во вариантов решений 3 6 4 8 5 10 6 12 7 14 8 16 9 18 10 20 i Xi=Xi-1 XiXi-1 всего решений 3 2 4 6 4 2 2+4=6 8 5 2 2+6=8 10 6 2 2+8=10 12 7 2 2+10=12 14 8 2 2+12=14 16 9 2 2+14=16 18 10 2 2+16=18 20
(X1 X2)(X1 X3)=1 (X2 X3)(X2 X4)=1 . (X8 X9)(X8 X10)=1 Решение при помощи графа: дерево 1 0 X1 X2 1 X3 1 0 0 1 1 0 1 0 0 2 4 6 1 0 X4 1 0 0 1 0 1 8 Ответ: 20 вариантов VI X1=0 X2 =1 X3=0 X1=1 X2 =0 X3=1 X1=0 X2 =0 X3=1 X1=1 X2 =1 X3=1 X1=0 X2 =0 X3=0 X1=1 X2 =1 X3=0 X2=0 X3 =1 X4=0 X2=1 X3 =0 X4=1 X2=0 X3 =0 X4=1 X2=1 X3 =1 X4=1 X2=0 X3 =0 X4=0 X2=1 X3 =1 X4=0
VII Сколько различных решений имеет система уравнений (X1 X2) (¬X1 ¬X2) (X2 X3) (¬X2 ¬X3) = 1 (X2 X3) (¬X2 ¬X3) (X3 X4) (¬X3 ¬X4) = 1 . (X8 X9) (¬X8 ¬X9) (X9 X10) (¬X9 ¬X10) = 1 где x1, x2, …, x10 – логические переменные? Применим закон замены эквивалентности: (X1 X2)(X2 X3)=1 (X2 X3)(X3 X4)=1 . (X8 X9)(X9 X10)=1 Решаем самостоятельно Ответ: 178 вариантов 1 0 X1 X2 1 X3 1 0 0 0 1 0 1 0 1 2 4 6 1 0 X4 0 0 1 1 0 1 10 1 0 0 1 0 0 1 1 0 1 0 1 1 0 1 0 0 1 X5 16
VII i всего решений 3 4 2 6 4 4+2=6 4 10 5 6+4=10 6 16 6 10+6=16 10 26 7 16+10=26 16 42 8 26+16=42 26 68 9 42+26=68 42 110 10 68+42=110 68 178
🎥 Видео
2.2 Итерационные методы решения СЛАУ (Якоби, Зейделя, релаксации)Скачать
Метод Ньютона (метод касательных) Пример РешенияСкачать
Численное решение уравнений, урок 3/5. Метод хордСкачать
КАК РЕШАТЬ СИСТЕМЫ ЛОГИЧЕСКИХ УРАВНЕНИЙ. ЕГЭ по информатике. Задание 23Скачать
11 класс, 27 урок, Общие методы решения уравненийСкачать
Решение системы уравнений методом ГауссаСкачать
Общие методы решения уравнений | Алгебра 11 класс #26 | ИнфоурокСкачать
ПОДГОТОВКА К ЕГЭ. ИНФОРМАТИКА. УРОК 2. РЕШЕНИЕ СИСТЕМЫ ЛОГИЧЕСКИХ УРАВНЕНИЙ МЕТОДОМ ОТОБРАЖЕНИЯСкачать
8 Метод простой итерации Ручной счет Решение системы линейных уравнений СЛАУСкачать
Конъюнкция, дизъюнкция, импликация, эквиваленция, отрицание. На примерах из жизни. Логика.Скачать
Сколько решений имеет логическое уравнение: (A импликация В) ИЛИ (C импликация D). ЕГЭ(информатика)Скачать
Метод половинного деления. ДихотомияСкачать
9 класс, 11 урок, Методы решения систем уравненийСкачать
Математика это не ИсламСкачать
Информатика 8 класс. Системы счисления. Решение уравненийСкачать
Решение системы уравнений методом Крамера 2x2Скачать
