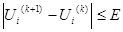Общая характеристика методов
Методы решения систем уравнений — прямые (точные) и итерационные (приближенные). Прямые применяются для решения систем линейных урав-нений, итерационные — для решения систем линейных и нелинейных уравне-ний.
Нелинейные уравнения установившегося режима формируются, если в узлах сети задана постоянная мощность(нагрузка или генерация).
Суть итерационных методов: задается некоторое начальное прибли-жение неизвестных U (0) , которое постепенно уточняется в ходе выполнения ряда однотипных шагов вычислений (итераций). Если итерационный про-цесс сходится, то получаем искомое решение U (*) с заданной точностью.
Итерациями называются многократно повторяющиеся однотипные ша-ги вычислений.
Основные характеристики итерационных методов:
1. Условия сходимости к решению, при которых происходит приближе-ние к искомому решению U (*) , либо удаление от него;
2. Скорость сходимости. Характеризуется количеством итераций n, необ-ходимых для достижения решения с заданной точностью, или законом изменения вектора погрешности при переходе от итерации к итерации;
2.3. 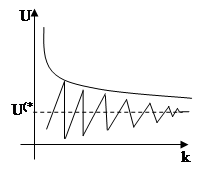
Возможно влияние на скорость сходимос-ти за счет введения дополнительных коэффици-ентов;
4. Необходимость хранения в памяти ЭВМ всех коэффициентов систем уравнений. Удобство программирования, простота алгоритмов и т.д.
Рассматриваем систему нелинейных уравнений установившегося режи-ма. В матричной форме она имеет вид:
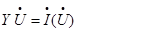
В развернутой форме такая система уравнений может быть представлена в следующем виде:

Преобразуем систему (2) квиду, пригодному для решения ее итераци-онными методами. Для этого каждое уравнение системы решим относитель-но одной из неизвестных величин Ui:
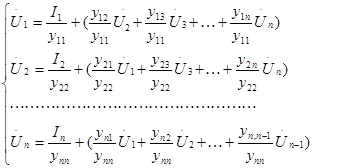
Любое i-ое уравнение этой системы можно записать в общем виде:
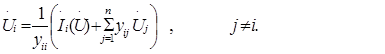
Если задать начальные приближения неизвестных U (0) , подставить их в правую часть уравнений (4) и выполнить необходимые вычисления, опреде-лим следующее приближение неизвестных U (1) и т.д. Такая после-довательность действий соответствует методу простой итерации. Тогда (4) в итерационной форме:
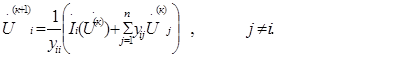
В матричной форме система (3) может быть записана следующим образом:
здесь 
D — вектор свободных членов, 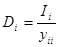
С — матрица коэффициентов при неизвестных, 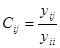
В итерационном виде система (5) принимает вид:
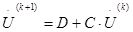
Здесь к – номер приближения неизвестных.
Общий алгоритм итерационных методов решения СНАУ установившегося режима
1) Задание начальных приближений вектора неизвестных U (0) =Uном.
Как правило, в качестве начальных приближений напряжений задают номи-нальные напряжения узлов Uном.В некоторых случаях, в качестве начальных приближений напряжений принимают значения, полученные в предыдущих близких расчетах для данной схемы;
2) Задание точности расчета E, предельного количества итераций nпред.,
начального значения счетчика итераций к=0 и других параметров расчета;
3) Выполнение итерации в соответствии с формулой (6):
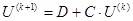
4) Контроль завершения итерационного процесса:
Если условие не выполняется, то изменяем счетчик итераций (к=к+1) и возвращаемся к пункту (3). Повторяем расчет при новых приближениях неизвестных.
Если условие выполняется для всех значений Ui, то итерационный процесс завершается, найденные на последней итерации приближения неизвестных U ( k +1) принимаются в качестве искомых значений с заданной точностью.
Итерационные методы дают последовательность приближенных значе-ний неизвестных, сходящуюся к точному решению. Это означает, что су-ществует предел последовательности:

здесь U (* ) — точное решение при 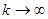
Таким образом, точное решение может быть получено лишь в резуль-тате бесконечного итерационного процесса. Всякий вектор U ( k ) , полученный на к-ой итерации, является приближенным решением системы уравнений.
Вектор погрешности этого приближенного решения:
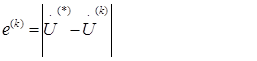
Так как точное решение U (*) заранее неизвестно, то о погрешности судят по разности значений на смежных итерациях (к+1) и к, то есть по вектору поправок:
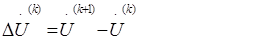
Если 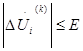
Такой подход к контролю завершения итерационного процесса — не единственный и не очень надежный, так как возможно такое незначительное изменение приближений от итерации к итерации даже вдали от решения.
Более строгим и надежным способом контроля завершения итераци-онных процессов является контроль невязок уравнений. Невязка уравнения – разность между левой и правой частями уравнения. Её значение получаем при подстановке в уравнения системы (2) очередного приближения неиз-вестных. Например, для 1-го уравнения:
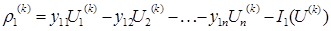
Для УУР невязка уравнения соответствует расчетному небалансу тока (мощ-ности) в узле. При подстановке точных значений неизвестных U1 (*) ,U2 (*) ,…,Un (*) невязки будут равны нулю:

То есть если итерационный процесс сошелся, то невязки близки к нулю. И чем дальше приближение Ui ( k ) от точного решения, тем больше величина не-вязок. В общем случае вектор невязок можно определить:
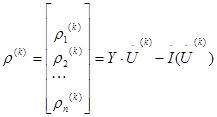
Итерационный процесс сошелся, если выполняются условия завершения итерационного процесса:

Это условие является более надежным критерием окончания итерационного процесса.
Достаточным условием сходимости итерационного процесса для урав-нений установившегося режима является:
Т.о. условие сходимости определяется только соотношением элементов матрицы проводимостей Y . В ней диагональные элементы Уіі (собственные проводимости узлов) неравны нулю. Как правило, диагональные элементы матрицы проводимостей больше или равны суммы недиагональных элемен-тов. Т.е. при правильном формировании матрицы, это условие сходимости выполняется всегда.
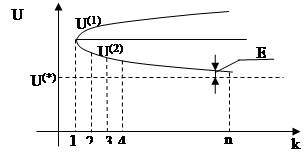
Два вида сходимости итерационных процессов:
1. Экспоненциальный (апериодический):
 |
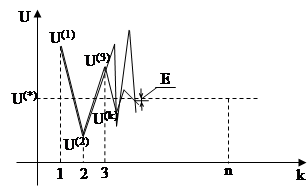
В случае не сходящихся или расходящихся итерационных процессов, нужно проверять правильность расчетов параметров схемы замещения, правильность расчета элементов и формирования матрицы проводимос-тей, анализировать величины токов и мощностей в заданных узлах.
Видео:11 класс, 27 урок, Общие методы решения уравненийСкачать

Пример использования метода Ньютона для решения УУН
УЧЕТ КОМПЛЕКСНОГО ХАРАКТЕРА
ПАРАМЕТРОВ СХЕМЫ ЗАМЕЩЕНИЯ И РЕЖИМА[1]
Система уравнений узловых напряжений для цепи переменного тока:
 . . | (9.7) |
При решении на ЭВМ системы уравнений узловых напряжений для сети переменного тока, как правило, она приводится к системе действительных уравнений порядка 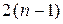

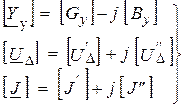 | (9.8) |
Подставляя (9.8) в (9.7), получим:
 | (9.9) |
Уравнение (9.9) переписываем, разделяя действительные и мнимые слагаемые.
 . . | (9.10) |
 . . | (9.11) |
Иными словами, систему уравнений узловых напряжений для цепи переменного тока можно записать в виде блочного матричного уравнения:
 | (9.12) |
Выражение (9.12) является системой действительных уравнений порядка 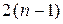
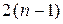
ОПИСАНИЕ РАСЧЕТА УР С ПОМОЩЬЮ ВЕКТОР-ФУНКЦИИ
Нелинейные уравнения установившегося режима в общей форме можно записать в виде системы неявных функций:
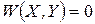 | (9.53) |
где 
Эти уравнения связывают между собой параметры установившегося режима электрической системы. Часть параметров режима задана (независимые переменные 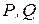

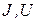

Число зависимых переменных 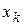




Разделение параметров режима на зависимые и независимые переменные играет важную роль при оптимизации режимов, при определении предельных по статической апериодической устойчивости режимов и при исследовании существования и единственности решения уравнений установившегося режима.
При расчетах установившегося режима вектор независимых переменных задан, то есть 
 | (9.54) |
Число уравнений в этой системе также равно числу зависимых переменных 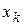

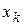
МЕТОД НЬЮТОНА
Метод Ньютона для решения систем нелинейных уравнений представляет собой обобщение на многомерный случай метода касательных, применяемого для решения одного нелинейного уравнения.
Идея метода Ньютона состоит в последовательной замене на каждой итерации системы нелинейных уравнений некоторой линейной системой, решение которой дает значения неизвестных, более близкие к решению нелинейной системы, чем исходное приближение. Поясним идею этого метода на примере решения уравнения
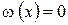 | (5.4) |
Решение уравнения 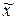 — точка, в которой кривая — точка, в которой кривая  проходит через нуль (рисунок 5.1): Рисунок 5.1- Графическая иллюстрация метода Ньютона проходит через нуль (рисунок 5.1): Рисунок 5.1- Графическая иллюстрация метода Ньютона |  |
Зададим начальное приближение к решению уравнения 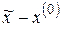
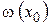

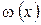

 | (5.5) |
Выражению (5.5) соответствует касательная к функции, проведенная в точке 
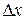
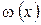

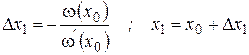 | (5.6) |
Полученную точку 
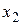
Аналогично определяется решение для системы нелинейных уравнений. Рекуррентное выражение, представленное в матричной форме записи, имеет вид:
 | (5.7) |
где 

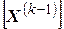

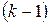
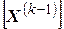
Пример использования метода Ньютона для решения УУН
Для электрической сети, представленной на рисунке 5.2, определить напряжения в узлах, используя метод Ньютона (три итерации).
Для рассматриваемой схемы электрической сети может быть записана система нелинейных УУН в форме баланса токов:
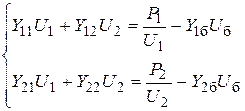 | (5.8) |
 | |
| Рисунок 5.2 | Схема электрической сети. |
Для решения методом Ньютона система УУН (5.8) представляется в форме баланса мощностей
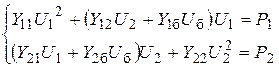 | (5.9) |
И приводится к виду
 |
Рекуррентное выражение метода Ньютона:
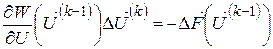 , , | (5.10) |
Где: 1) элементы матрицы Якоби вычисляются по формулам:
 , , |
2) вектор невязок вычисляется в точке 
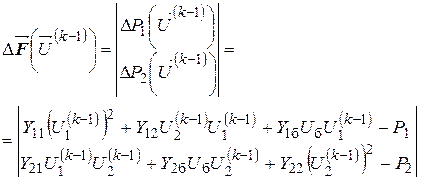 , , |
3) 
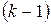

Новые напряжения вычисляются по выражению
 | (5.11) |
Для схемы электрической сети, представленной на рисунке 5.2, исходная система (5.9) имеет вид:
 |
Начальное приближение: 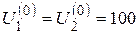
Вектор невязок записывается:
Элементы матрицы Якоби:
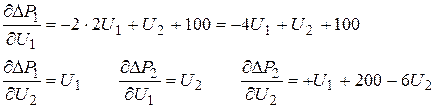 |
Для заданного начального приближения 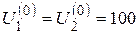
 |
Подставляем все найденные величины в 
 |
Решив ее, находим:
 |
По выражению (5.11):
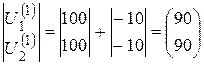 кВ кВ |
 |
 |
Система двух линейных уравнений:
 |
Решив ее, находим:
 |
По выражению (5.11):
 кВ кВ |
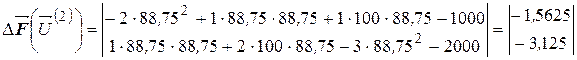 |
 |
Система двух линейных уравнений:
 |
Решив ее, находим:
 |
По выражению (5.11):
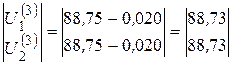 кВ кВ |
Вектор невязок для 4-ой итерации составил бы:
Видео:Методы решения уравненийСкачать

Уравнения узловых напряжений
Уравнения узловых напряжений (УУН) — система нелинейных (иногда линейных) алгебраических уравнений, в которых неизвестными являются напряжения в узлах электрической сети, наиболее часто применяемая для расчёта установившегося режима электрической сети.
Видео:Переходные процессы | Классический метод расчета переходных процессов. Теория и задачаСкачать

Содержание
Видео:9 класс, 11 урок, Методы решения систем уравненийСкачать

Описание
Установившийся режим электрических систем можно рассчитывать при различных способах задания исходных данных в зависимости от физической сути и цели расчёта. В статье рассмотрен наиболее часто встречающийся и наиболее простой случай, когда известны сопротивления и проводимости всех пассивных элементов электрической сети. Кроме того, заданы постоянные величины всех значений токов (мощности) во всех узлах, кроме балансирующего и все ЭДС, а также напряжение одного узла — базисного. При этом необходимо определить напряжения всех [math](n-1)[/math] узлов и токи во всех m ветвях.
В общем случае базисный по напряжению и балансирующий узлы могут не совпадать. Как правило, при расчётах режимов электрических систем предполагают, что эти узлы совпадают, в дальнейшем для простоты изложения предполагается, что базисным по напряжению и балансирующим является один и тот же [math]n[/math] -й узел. Число независимых уравнений по первому закону Кирхгофа равно числу независимых узлов [math](n-1)[/math] . Уравнение первого закона Кирхгофа для [math]n[/math] -го узла является следствием уравнений для остальных [math](n-1)[/math] узлов и не входит в число независимых уравнений.
Если в качестве неизвестных принять [math](n-1)[/math] узловых напря¬жений, то установившийся режим можно описать только узловыми уравнениями, вытекающими из первого закона Кирхгофа и закона Ома [1] , [2] , [3] , [4] . Уравнения узловых напряжений следуют из первого закона Кирхгофа, если все токи в ветвях выразить через узловые напряжения и проводимости ветвей. Число уравнений узловых напряжений равно числу независимых узлов [math](n-1)[/math] .
Уравнения баланса токов представляют собой простейшую форму уравнений, описывающих установившиеся режимы. Существуют две математические модели уравнений узловых напряжений:
Отличительной особенностью этих моделей является то, что линейная модель предполагает задание комплексных значений токов, в отличие от нелинейной модели, которая предполагает задание активной и реактивной мощностей. В большинстве задач нагрузки в узлах задаются активной и реактивной мощностями, по этой причине обычно используется нелинейная модель.
Видео:Общие методы решения уравнений | Алгебра 11 класс #26 | ИнфоурокСкачать

Вывод уравнений узловых напряжений
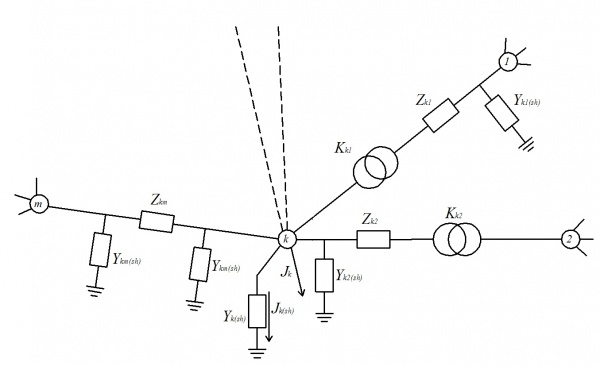
Для формирования УУН рассмотрим представленную на рис. 1 часть схемы замещения:
Первый закон Кирхгофа для к-го узла:
Наличие знака сопряжения в этом выражении обусловлено тем, что для идеального двухобмоточного трансформатора выполняется закон сохранения мощности [math]dot=dot=hatdot=hatdot[/math] , где индексами «Н» и «В» обозначены соответственно низшая и высшая обмотки трансформатора, поэтому, если [math]dot=dotdot<K_>[/math] , то из закона сохранения следует:
Подстановка полученных выражений в уравнение (1.1) с приведением подобных членов позволяет получить уравнение для k-го узла в виде:
Видео:c23 5, Корреляционная система уравнений: установившийся режимСкачать

В прямоугольной системе координат
В данной системе комплексные величины [math]displaystyle underline_, dot<U_>, dot<J_>[/math] представляются в виде
для проводимости справедливо следующее:
получаем, что [math]displaystyle underline=g-jb,[/math]
но для удобства расчёта матрицы проводимостей будем использовать соотношение
Запишем УУН для линейной ЭЭС:
левая часть данной системы характеризует токи, втекающие в k-й узел, правая часть — токи, вытекающие из того же узла, но с учетом влияния токов базы.
Подставляем (1), (2), (3) в (4), [math]dot_б[/math] представим аналогично уравнению (1), тогда имеем следующее:
[math]displaystyle begin sum_^ left( g_ + j b_ right) left( U_’ + j U_» right) = J_‘ + j J_»- left( g_ + j b_ right) left(U_’ + j U_»right), i = 1 ldots N end.[/math]
Сгруппируем и приведем подобные:
Сгруппируем относительно [math]j[/math] левую и правую части системы (5). Два комплексных числа равны, если равны их действительные и мнимые составляющие. Распишем в новой системе отдельно действительные и мнимые части. Получаем:
Представим данную систему (6) в матричной форме:
В случае, если [math]dot_б=U_б+j0,[/math] система (6) преобразуется к виду:
Соответственно упрощается матричная форма записи системы (8):
Вернемся к нелинейной модели ЭЭС. Для этого перенесем составляющую токов базы системы (4) в левую часть, изменив при этом диапазон [math]i=1 ldots (N-1)[/math] . Получаем:
Добавим, что [math]dot = P + j Q.[/math] (12)
Подставляем (11) в выражение (10), получаем следующее:
Подставляем (1), (3), (12) в (13), получаем:
[math]displaystyle begin sum_^ left( g_ + j b_ right) left( U_’ + j U_» right) = frac
, i = 1 ldots (N-1)end.[/math]
Раскрываем скобки, домножаем правую часть на сопряженное и группируем относительно [math]j[/math] :
Вынесем [math]j[/math] за знак суммы в левой части, а в правой части разобьем дробное выражение на две составляющие относительно [math]j[/math] , получим:
Преобразуем систему (14) к виду, аналогичному системе (8), и получаем нелинейную систему УУН для сети переменного тока в прямоугольных координатах в форме баланса токов:
Выведем систему нелинейных УУН для сети переменного тока в прямоугольных координатах в форме баланса мощностей. Для этого домножим систему (13) на [math]hat[/math] , получаем:
[math]displaystyle beginleft(U_i’-jU_i»right)sum_^left(g_+jb_right)left(U_’+jU_»right)=P_i-jQ_iend, i=1 ldots (N-1).[/math]
Вносим сопряженный комплекс напряжения под знак суммы и группируем относительно [math]j[/math] , имеем:
Преобразуем систему (17) к виду, аналогичному системе (15), и получаем нелинейную систему УУН для сети переменного тока в прямоугольных координатах в форме баланса мощностей:
Видео:Бакалавриат_ЭЭ_7 семестр_ПЭП_Математические методы расчета установившихся режимов СЭС_Лекция 3Скачать

В полярной системе координат
Комплексное число можно представить в алгебраической, показательной и тригонометрической формах:
[math]displaystyle dot=U_k’+jU_k» = V_k cdot e^ = V_k big(cos(δ_k)+j sin(δ_k)big).[/math]
Для того, чтобы вывести УУН в форме баланса мощностей в полярной системе координат, необходимо в систему (16) подставить показательную запись комплексного числа [math]dot[/math] . Выполнив это, получим:
[math]displaystyle begin V_i e^ sum_ limits^ (g_ + j b_) cdot V_k cdot e^ = P_i — j Q_i end, i= overline.[/math]
Переносим экспоненты в одну сторону:
[math]displaystyle begin V_isum_limits^V_k(g_+jb_) cdot e^ cdot e^=P_i-jQ_iend, i= overline.[/math]
Используя свойство степеней, выполним преобразования:
[math]displaystyle begin V_isum_limits^ V_k (g_+jb_) cdot e^ = P_i — jQ_iend, i= overline.[/math]
Переходим к тригонометрической форме:
[math]displaystyle begin V_isum_limits^ V_k bigg( big(g_ + jb_ big) big( cos(δ_k-δ_i) + j cdot sin(δ_k-δ_i) big) bigg) = P_i-jQ_i end, i= overline.[/math]
Группируем относительно [math]j[/math] :
Преобразуем систему (19) к виду, аналогичному системе (15), и получаем нелинейную систему УУН для сети переменного тока в полярных координатах в форме баланса мощностей:
Видео:Методы решения уравненийСкачать

Методы решения
Основные методы решения системы уравнений узловых напряжений:
- Метод Гаусса-Зейделя — это один из самых первых разработанных методов. Обычно показывает более медленную сходимость по сравнению с другими итерационными методами. Основными особенности — это малое использование памяти и не требуется матричная алгебра.
- Метод Якоби.
- Метод Z-матриц.
- Метод Ньютона-Рафсона — один из самых популярных методов решения, основанный на разложении в ряд Тейлора.
- Метод голоморфного встраивания — прямой метод расчёта на основе комплексного анализа.
🔥 Видео
5 способов решения уравнений | Эрик Легион | 100балльный репетиторСкачать

Метод решения уравнений, чтобы не ошибаться в знакахСкачать

Алгебра 11 класс (Урок№49 - Уравнения. Методы решения уравнений.)Скачать

МЗЭ 2021 Лекция 11 Метод Ньютона для решения систем нелинейных уравненийСкачать

Алгебра 11 класс (Урок№50 - Системы уравнений. Методы решения систем уравнений.)Скачать

Нестандартные методы решения уравнений, неравенств, систем. (часть 1).Скачать

Метод Ньютона (метод касательных) Пример РешенияСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Решение биквадратных уравнений. 8 класс.Скачать

Матричный метод решения систем уравненийСкачать

7 класс, 35 урок, Графическое решение уравненийСкачать