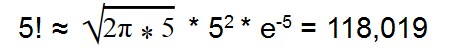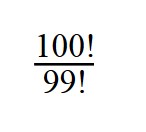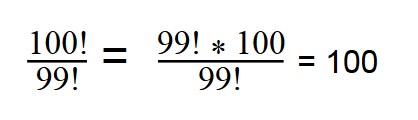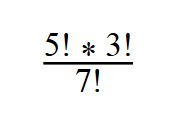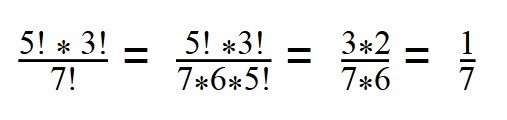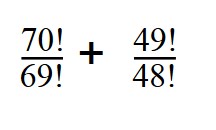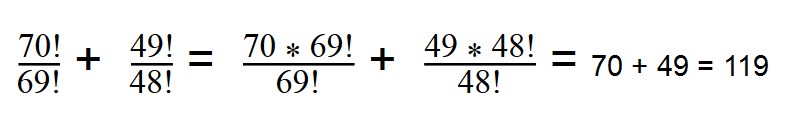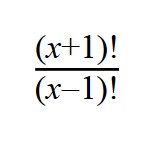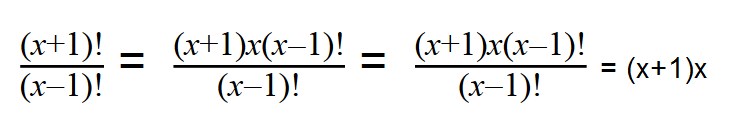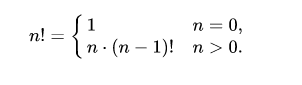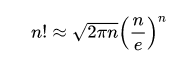О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
- Факториал: определение
- Формулы и свойства факториала
- Примеры решений
- Факториал — формула, свойства и примеры решений
- Таблица факториалов
- Свойства факториалов
- Рекуррентная формула
- Комбинаторная интерпретация
- Формула Стирлинга
- Расчет по предыдущему значению
- Некоторые очень большие значения
- Методы решения уравнений с факториалами
- Как решать уравнения с факториалами
- Таблица факториалов
- Примеры решения факториалов
- 5. ФАКТОРИАЛ
- Как посчитать факториал
- Вам понадобится
- Инструкция
- 💡 Видео
Видео:Как решить уравнение с факториалами | Подходы и методы решенияСкачать

Факториал: определение
Факториал числа n — это произведение натуральных чисел от 1 до n. Обозначается n, произносится «эн-факториал».
Факториал определен для целых неотрицательных чисел. Это значит, что вот так нельзя:
Число должно быть целое и положительное:
- 3! 56! 12!
| Формула факториала n!=1⋅2⋅3⋅. ⋅(n−2)⋅(n−1)⋅n |
Вычисляется факториал по формуле: путем умножения всех чисел от одного до значения самого числа под факториалом. Факторизация — это разложение функции на множители.
Мы видим, что 4! — это 3!*4
5! — это 4!*5
6! — это 5!*6
Видео:Решите уравнение ➜ ДВИ до ЕГЭСкачать

Формулы и свойства факториала
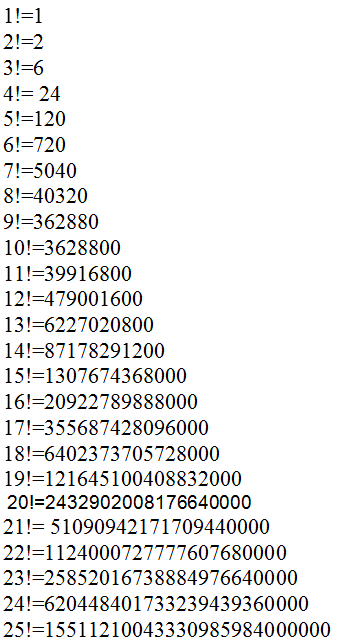
Чтобы узнать, как вычислять факториалы быстро — воспользуемся табличкой. Сохраняйте себе и решайте раньше остальных.
| 1! = 1 |
| 2! = 2 |
| 3! = 6 |
| 4! = 24 |
| 5! = 120 |
| 6! = 720 |
| 7! = 5040 |
| 8! = 40320 |
| 9! = 362880 |
| 10! = 3628800 |
| 11! = 39916800 |
| 12! = 479001600 |
| 13! = 6227020800 |
| 14! = 87178291200 |
| 15! = 1307674368000 |
| 16! = 20922789888000 |
| 17! = 355687428096000 |
| 18! = 6402373705728000 |
| 19! = 121645100408832000 |
| 20! = 2432902008176640000 |
| 21! = 51090942171709440000 |
| 22! = 1124000727777607680000 |
| 23! = 25852016738884976640000 |
| 24! = 620448401733239439360000 |
| 25! = 15511210043330985984000000 |
Факториалов в математике 9 класса — полно. Чтобы всегда быть готовым решить пример, запомните основные формулы:
- (n — 1)! = 1*2*3*4*5*. *(n — 2)(n — 1)
- n! = 1*2*3*4*5*. *(n — 2)(n — 1)n
- (n + 1)! = 1*2*3*4*5*. *(n — 2)(n — 1)n(n + 1)
С помощью формулы Стирлинга можно вычислить факториал многоразрядных чисел.
Такая формула дает результат с небольшой погрешностью.
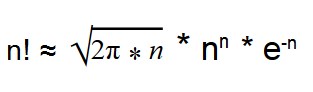 |
Рекуррентная формула
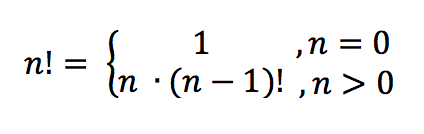 |
- 5! = 5*(5 — 1)! = 5*4! = 5*24 = 120
- 6! = 6*(6-1)! = 6*5! = 6*120 = 720
Для решения примеров обращайтесь к таблице.
Примеры умножения факториалов:
- Пользуйтесь готовой таблицей 5! * 7! = 120 * 5040 = 604800
- Или раскладывайте факториалы отдельно, если хотите потренироваться:
5! = 1*2*3*4*5 = 4! * 5 =120
7! = 1*2*3*4*5*6*7 = 6! * 7 = 5040
120 * 5040 = 604800
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Видео:Решите уравнение c факториаламиСкачать

Примеры решений
Давайте поупражняемся и решим пару примеров.
1. Сократите дробь:
При сокращении факториалов, пользуйтесь свойством:
n! = (n — 1)! * n
100! = 99! * 100
Далее сокращаем по принципу сокращения обыкновенных дробей.
2. Вычислите значение выражения с факториалом: 8! + 5!
Можно для решения факториалов воспользоваться таблицей и вычислить быстрее.
А можно потренироваться и разложить их:
8! = 1*2*3*4*5*6*7*8 = 7!*8 = 5040 * 8 = 40320
5! = 1*2*3*4*5 = 4!*5 = 120
40320 + 120 = 40440
8! + 5! = 40440
3. Вычислите значение выражения:
7! = 1*2*3*4*5*6*7 = 5! * 6 *7
Далее сокращаем все, что можем сократить (3*2=6, сокращаем числа 6) и получаем ответ.
4. Вычислите значение выражение:
Вы уже знаете, как найти факториал — раскладываем 70 и 49:
70! = 1*2*3*. *69 = 69! * 70
49! = 1*2*3*. 49! * 48
Далее сокращаем все одинаковые множители.
5. Сократите дробь:
Проводим разложение на множители при помощи формул сокращенного умножения (x+1)x(x-1) и сокращаем все одинаковые множители (x-1)!.
Если вы все еще считаете, что факториал бесполезен и не может помочь вам в жизни, то это не так. Он помогает легко вычислять вероятности (а это бывает нужно чаще, чем кажется). К тому же, комбинаторика необходима тем, кто собирается работать в IT. Поэтому решайте побольше задачек на факториалы, в мире будущего без них — никуда.
Видео:Уравнение с факториаламиСкачать

Факториал — формула, свойства и примеры решений
Факториал числа n – это произведение чисел от 1 до n. Определён только для целых неотрицательных чисел. Формула факториала:
Математическая формула представлена восклицательным знаком «!». Термин был введен в 1800 году, а обозначение появилось только в 1808. В формуле нужно умножить все целые числа от 1 до значения самого числа, стоящего под знаком факториала.
Это очень просто, вот пример:
7! = 1 * … * 7 = 5040.
Факторизация — разложение функции на множители.
Видео:ФакториалСкачать

Таблица факториалов
Видео:Как решают уравнения в России и СШАСкачать

Свойства факториалов
Рекуррентная формула
Комбинаторная интерпретация
Функция n может интерпретироваться как количество перестановок. К примеру, для 3-х элементов есть 3! = 6 перестановки.
Формула Стирлинга
Позволяет не перемножать большие числа. Обычно необходим только главный член:
Можно ли вычислить 0,5 или -3,217? Нет, нельзя. Но можно использовать нечто под названием «Гамма-функция», что намного сложнее.
Расчет по предыдущему значению
Функцию легко вычислить из предыдущего значения:
А как вычислить факториал нуля? Если вернуться к определению, то видно, что применять его в случае «0» нет смысла. Положительных чисел до 0 нет, поэтому 0 x 0 = 0.
Однако было решено, что в случае 0 результат будет равен 1.
Некоторые очень большие значения
Онлайн калькулятор поможет сделать вычисление – всего лишь надо найти знак, похожий на «x!» или «n!». Нужно обратить внимание, что браузеры могут испытывать затруднения при попытке отобразить более крупные числа и может произойти сбой.
Некоторые браузеры могут не позволять копировать, поэтому необходимо будет загрузить большие результаты в виде текстового файла.
Примеры вычисления факториалов больших чисел:
70! приблизительно 1 19785716669969869891796072783721 x 10100, что немного больше, чем «гуголь» (1 и 100 нулей);
100! это примерно 9 33262154444944152681699238856 x 101576 x 10157;
200! это примерно 7 88657867867364479050355236321393 x 103743.
Как найти функцию в Паскаль? Вычисление легко реализуется на разных языках программирования. Можно выбрать два метода: итеративный, то есть он создает цикл, в котором временная переменная умножается на каждое натуральное число от 1 до n, или рекурсивный, в котором функция вызывает себя до достижения базового варианта 0! = 1.
Программа на языке Паскаль:
На языке Си вычисления делаются с помощью рекурсивной функции. Следует заметить, что если начать вычислять факториал отрицательного числа в неаккуратно написанной функции, то это приведет к зацикливанию.
Факториал дроби (½) — это половина квадратного корня pi = (½)√π.
Видео:Факториалы - быстрое вычисление | Профильная математикаСкачать

Методы решения уравнений с факториалами
Элементы комбинаторики
И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Теория вероятностей и математическая статистика − разделы математики, наиболее широко используемые в самых различных областях деятельности от маркетинговых исследований до социального прогнозирования. Для успешного овладения навыками решения прикладных задач необходимо освоить основные теоретические и практические аспекты теории вероятностей и математической статистики.
При решении вероятностных задач часто используются формулы комбинаторики – одного из разделов математики, который изучает различные комбинации, составленные из заданного конечного множества различимых между собой объектов различной природы (буквы алфавита, цифры, предметы и др.).
Определение.Факториалом натурального числа n называется произведение всех натуральных чисел от n до
Факториал натурального числа n обозначается n! и читается «эн факториал»

Факториал нуля равен единице
Пример 3.1.Сократить дробь:
Пример 3.2. Сократить дробь:
Дата добавления: 2014-10-15; Просмотров: 1484; Нарушение авторских прав?;
- Установите .
- Создать
- F = вход? Если да, то является N.
- Если нет, то установите , а затем снова начните с # 2.
Вы можете оптимизировать, используя предыдущий результат для вычисления нового ( ).
Это так же быстро, как движение в противоположном направлении, если не быстрее, учитывая, что разделение обычно занимает больше времени, чем умножение. Данный факториал гарантировано, что все целые числа, меньшие, чем качестве факторов в дополнение к А, так что вы потратили бы столько времени на факторинг, как вы просто вычисляли бы факториал.
Ну, если вы знаете, что M действительно является факториалом какого-то целого, то вы можете использовать
Вы можете решить эту проблему (или, действительно, решить ) и найти ближайшее целое число. Он все еще нелинейный, но вы можете легко получить приближенное решение путем итерации (на самом деле, я ожидаю, что коэффициент достаточен).
Вот код clojure:
Пусть n = 120, div = 2. 120/2 = 60, 60/3 = 20, 20/4 = 5, 5/5 = 1, возврат 5
Пусть n = 12, div = 2. 12/2 = 6, 6/3 = 2, 2/4 = .5, return ‘nil’
Если вы не знаете , является ли число или нет, достойным тестом является проверка, если он делится на все мелкие простые числа, пока приближение Стерлинга этого числа больше, чем В качестве альтернативы, если у вас есть таблица факториалов, но она не подходит достаточно высоко, вы можете выбрать самый большой фактор в своей таблице и убедиться, что делится на это.
В C из моего приложения Advanced Trigonometry Calculator v1.6.8
Что вы думаете об этом? Правильно работает для целых чисел факториалов.
Большинство чисел не находятся в диапазоне выходов факториальной функции. Если это то, что вы хотите проверить, легко получить приближение, используя формулу Стирлинга или количество цифр целевого номера, как упомянуто другими, а затем выполнить бинарный поиск, чтобы определить факториалы выше и ниже заданного числа.
Более интересным является построение обратной функции Гамма, которая расширяет факториальную функцию до положительных действительных чисел (и к наиболее сложным числам тоже). Оказывается, что построение обратного является трудной задачей. Тем не менее, он был определен явно для большинства положительных реальных чисел в 2012 году в следующем документе: http://www.ams.org/journals/proc/2012-140-04/S0002-9939-2011-11023-2/S0002- 9939-2011-11023-2.pdf . Явная формула приведена в следствии 6 в конце статьи.
Обратите внимание, что он включает интеграл в бесконечной области, но при тщательном анализе я считаю, что разумная реализация может быть построена. То, что лучше, чем простая схема последовательных приближений на практике, я не знаю.
Видео:11 класс, 27 урок, Общие методы решения уравненийСкачать

Как решать уравнения с факториалами
очень легко оценить. Поэтому продолжайте делиться на 2,3,5,7 … и проверьте экспоненты, сколько раз вы могли бы разделить.
Теперь вопрос в том, что у вас есть n! что представляет собой показатель простого p в нем?
Во-первых, n! может иметь только простые числа вплоть до n, включая n, если он является простым.
Вы добавляете один за каждый раз простой p, или любая его сила находится в пределах n. Сколько раз вы увидите p. Ну, это должен быть самый большой k, для которого
то же самое от премьер-министра
Предположим, что у нас есть 10888869450418352160768000000
Мы можем разделить
не делится на 29
Это означает, что это число от 23 до 29. (Обычно диапазон намного больше, но этот пример по-прежнему полезен).
Теперь мы можем использовать бинарный поиск между 23 и 29, чтобы получить набор, который можно разделить на 2, 23 раза. Обратите внимание, что может быть только два таких числа. Мы пробуем 26 и легко обнаруживаем, что это
Если это не так, мы продолжим сегмент 23-26 или 26-29 в зависимости от результата.
Таким образом, это либо 26, либо 27. Мы делаем то же самое для 3 и остальных, пока не получим совпадение ни с одним из двух возможных чисел. Числа будут иметь разный результат для хотя бы одного из заданных простых чисел.
Поэтому, если вышеперечисленное является факториалом, это факторный показатель 27. Проверка того же, что и выше для 5,7,11,13,17,19 и 23, показывает, что все в порядке и что это действительно 27.
Видео:ФакториалСкачать

Таблица факториалов
| 1! | 1 |
| 2! | 2 |
| 3! | 6 |
| 4! | 24 |
| 5! | 120 |
| 6! | 720 |
| 7! | 5 040 |
| 8! | 40 320 |
| 9! | 362 880 |
| 10! | 3 628 800 |
| 11! | 39 916 800 |
| 12! | 479 001 600 |
| 13! | 6 227 020 800 |
| 14! | 87 178 291 200 |
| 15! | 1 307 674 368 000 |
| 16! | 20 922 789 888 000 |
| 17! | 355 687 428 096 000 |
| 18! | 6 402 373 705 728 000 |
| 19! | 121 645 100 408 832 000 |
| 20! | 2 432 902 008 176 640 000 |
| 21! | 51 090 942 171 709 440 000 |
| 22! | 1 124 000 727 777 607 680 000 |
| 23! | 25 852 016 738 884 976 640 000 |
| 24! | 620 448 401 733 239 439 360 000 |
| 25! | 15 511 210 043 330 985 984 000 000 |
| 26! | 403 291 461 126 605 635 584 000 000 |
| 27! | 10 888 869 450 418 352 160 768 000 000 |
| 28! | 304 888 344 611 713 860 501 504 000 000 |
| 29! | 8 841 761 993 739 701 954 543 616 000 000 |
| 30! | 265 252 859 812 191 058 636 308 480 000 000 |

Определение (что такое факториал) Факториал числа — результат последовательного умножения числа на все натуральные числа меньшие данного числа и большие единицы. Обозначается факториал восклицательным знаком после числа — «n!». Факториал натурального числа n можно также определить как рекуррентную функцию F (n). Определяется она следующим образом: F (0) = F (1) = 1; F (n) = n * F (n-1). Пример: 7! = 7×6×5×4×3×2×1 = 5040 Не стоит забывать По общепринятой договоренности 0! = 1 (факториал нуля равен единице). Этот факт важен, к примеру, для вычисления биномиальных коэффициентов. Полезный факт Факториал числа, функцию от натурального аргумента можно продолжить на все действительные числа с помощью т.н.
Видео:Сокращение дробей с факториаламиСкачать

Примеры решения факториалов
Гамма-функции (важно отметить, что для этого требуется определенный математический аппарат). В таком случае, мы сможем посчитать факториал любого действительного числа. Например, факториал (или, Гамма-функция, что математически правильнее) числа Пи Π! приблизительно равен 2.28803779534. Факториал числа Эйлера, другого трансцендентного числа, Γ(e)
1.567468255 (упрощенно, факториал числа e).
| Если у вас есть мысли по поводу данной страницы или предложение по созданию математической (см. раздел «Математика») вспомогательной памятки, мы обязательно рассмотрим ваше предложение. Просто воспользуйтесь обратной связью. |
© Школяр. Математика (при поддержке «Ветвистого древа») 2009—2016
Видео:Комбинаторное уравнениеСкачать

5. ФАКТОРИАЛ
Определение.Факториалом натурального числа n называется произведение всех натуральных чисел от n до
Факториал натурального числа n обозначается n! и читается «эн факториал»

Факториал нуля равен единице
Пример 3.1.Сократить дробь:
Пример 3.2. Сократить дробь:
Дата добавления: 2015-05-12; просмотров: 1702; Опубликованный материал нарушает авторские права? | Защита персональных данных |
Не нашли то, что искали? Воспользуйтесь поиском:
Видео:Уравнение с факториалами | Из пушки по воробьямСкачать

Как посчитать факториал
Видео:9 класс. Алгебра. Факториалы.Скачать

Вам понадобится
Видео:Комбинаторика: перестановка, размещение и сочетание | Математика | TutorOnlineСкачать

Инструкция
- Чтобы посчитать факториал натурального числа перемножьте все натуральные числа, не превосходящие данное. Каждое число учитывается только один раз. В виде формулы это можно записать следующим образом:n! = 1*2*3*4*5*…*(n-2)*(n-1)*n, гдеn – натуральное число, факториал которого требуется посчитать.
0! принимается равным единице (0!=1).При возрастании аргумента значение факториала очень быстро увеличивается, поэтому обычный (бухгалтерский) калькулятор уже для факториала 15-ти вместо результата может выдать сообщение об ошибке. - Чтобы посчитать факториал большого натурального числа, возьмите инженерный калькулятор. То есть, такой калькулятор на клавиатуре которого имеются обозначения математических функций (cos, sin, √). Наберите на калькуляторе исходное число, а затем нажмите кнопку вычисления факториала. Обычно такая кнопка обозначается как «n!» или аналогично (вместо буквы «n» может стоять «N» или «х», но восклицательный знак «!» в обозначении факториала должен присутствовать в любом случае).
При больших значениях аргумента результаты вычислений начинают отображаться в «экспоненциальном» (показательном) виде. Так, например, факториал 50 будет представлен в форме: 3,0414093201713378043612608166065e+64 (или похожем). Чтобы получить результат вычислений в обычном виде, припишите к числу, показанному до символа «е», столько нулей, сколько указано после «е+» (если, конечно, хватит места). - Чтобы посчитать факториал числа на компьютере, запустите программу «калькулятор» (стандартный калькулятор Windows). Для этого найдите его изображение на рабочем столе или нажмите на кнопки «Пуск» и «Выполнить». Затем, наберите в появившемся окошке «calc» и нажмите «Ок». Посмотрите: в каком режиме запустилась программа «Калькулятор». Если картинка напоминает обыкновенный «бухгалтерский» калькулятор, переключите его в «инженерный» режим. Для этого, просто щелкните мышкой на пункте «Вид» и выберите в списке опций строку «Инженерный».
После чего, проделайте те же самые действия, которые перечислены в предыдущем пункте инструкции — наберите число и нажмите кнопку «n!». - «Посчитать» факториал числа можно и без использования вычислительной техники. Для этого просто распечатайте таблицу факториалов. Так как значения факториала очень быстро увеличиваются, то реально распечатать лишь факториалы чисел от 0 до 50.
Однако, практическое применение таких таблиц весьма сомнительно. Ведь, во-первых, на ввод такого многозначного числа уйдет очень много времени, во-вторых, велика вероятность ошибки при вводе, а, в-третьих, не совсем понятно – куда вводить такое длинное число. Ни на дисплее калькулятора, ни в ячейке Excel просто не уместится так много цифр.
Слово факториал произошло от латинского factor (делающий, производящий).
Факториал числа — это произведение натуральных чисел от 1 до самого числа (включая данное число).
Обозначается факториал восклицательным знаком «!».
- 3! = 1 · 2 · 3 = 6
- 6! = 1 · 2 · 3 · 4 · 5 · 6 = 720
Факториал определён только для натуральных чисел и нуля.
Факториал нуля и единицы это 1.
Термин факториал ввел в 1800 году францзузский математик Аргобаст Луи Франсуа Антуан.
Обозначение «n!» придумал чуть позже немецкий математик Кристиан Крамп в 1808 году.
Интересные факториалы проверьте сами:
+ 4! + 5! = 1 + 24 + 120 = 145
На нашем ресурсе вы также можете посчитать факториал онлайн.
💡 Видео
Уравнение с факториалами в натуральных числахСкачать

Что такое факториал | МатематикаСкачать

Уравнение с факториаламиСкачать

Факториалы — это легко! Показываю, что это такое и как решать этот примерСкачать

Сможешь сократить дробь с факториалами?Скачать

Уравнение от подписчикаСкачать