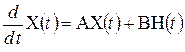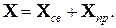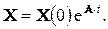Как известно, переходный процесс в любой цепи определяется не только параметрами входящих в нее элементов, но и независимыми начальными (t=0+) условиями — токами через индуктивности 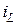
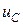
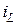
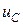
Действующие в цепи источники называются входными переменными 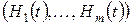
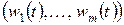
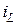
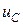
Для линейных цепей система уравнений состояния является линейной и может быть записана в виде набора дифференциальных уравнений первого порядка, которые можно представить в виде матричного уравнения:
или в более компактной форме
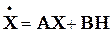
где 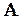
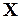
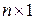
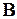
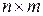
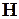
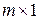
Расчет цепей методом переменных состояния можно разделить на два этапа:
1) составление системы дифференциальных уравнений цепи;
2) решение составленной системы дифференциальных уравнений.
Составить систему дифференциальных уравнений цепи можно различными способами, например, с применением метода наложения или непосредственно из системы уравнений, записанных по законам Кирхгофа, путем исключения токов и напряжений резистивных элементов. Однако совместное решение уравнений Кирхгофа при увеличении числа ветвей цепи становится все более громоздким.
Уравнения состояния можно формировать и сразу в матричной форме, как показано в [1].
Решение системы дифференциальных уравнений, составленных методом переменных состояния, можно выполнить как аналитически, так и численными методами.
При аналитическом решении уравнения состояния записываются в виде суммы матриц свободной — 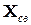
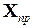
Здесь 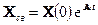
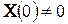
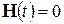
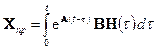
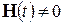
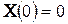
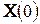
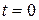
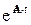
Таким образом, если в цепи после коммутации нет источников энергии, т.е. 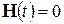
Если же после коммутации имеются источники независимых воздействий, то матрица 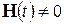
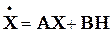
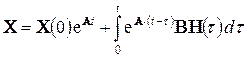
Это решение состоит из суммы двух слагаемых — реакции цепи при ненулевых начальных условиях и реакции цепи при нулевых начальных условиях и наличии источников внешних воздействий 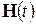
Главная трудность расчета аналитическим методом заключается в вычислении матричной экспоненциальной функции. Матричную функцию вычисляют по формуле (теореме) Сильвестра [2]:
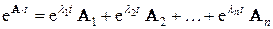
где 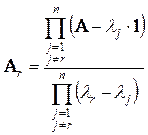
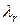
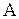
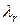
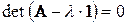
где 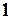
Характеристические числа 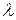
Дата добавления: 2015-02-16 ; просмотров: 1098 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:9 класс, 11 урок, Методы решения систем уравненийСкачать

Методы решения уравнений состояния электрических систем
СОДЕРЖАНИЕ
1.ПРОГРАММА КУРСА. . . . . . . . . . . . . . . . 4
1.1 Техническая постановка задачи расчета и анализа
установившихся режимов электрических систем. . . . . . 4
1.2 Уравнения состояния электрических систем . . . . . . 5
1.3 Методы решения уравнений состояния электрических систем . 5
1.4 Анализ статической устойчивости электрических систем. . . 6
2.ОСНОВЫ РАСЧЕТА И АНАЛИЗА УСТАНОВИВШИХСЯ РЕЖИМОВ
ЭЛЕКТРИЧЕСКИХ СИСТЕМ. . . . . . . . . . . . . . . 7
2.1 Техническая постановка задачи. . . . . . . . . . 7
2.2 Расчет установившегося режима с использованием
линейных математических моделей . . . . . . . . . 9
2.3 Уравнения состояния ЭС. . . . . . . . . . . . . 12
2.4 Пример расчета на основе линейной модели. . . . . . . 15
2.5 Реализация расчета режима в среде Mathcad . . . . 19
2.6 Задание № 1 по контрольной работе. . . . . . . . . 23
3.МАТЕМАТИЧЕСКИЕ МЕТОДЫ АНАЛИЗА СТАТИЧЕСКОЙ УСТОЙЧИВОСТИ
УСТАНОВИВШИХСЯ РЕЖИМОВ. . . . . . . . . . . . . . . 23
3.1 Техническая постановка задачи. . . . . . . . . . .23
3.2 Пример анализа статической устойчивости по корням
характеристического уравнения. . . . . . . . . . . 24
3.3 Пример анализа устойчивости по критерию Гурвица. . . . .28
3.4 Пример использования критерия Михайлова
для анализа статической устойчивости. . . . . . . . 31
3.5 Реализация задачи анализа устойчивости в среде Mathcad . .33
3.6 Задание №2 для контрольной работы. . . . . . . . . 35
ВВЕДЕНИЕ
Целью данного курса является ознакомление студента с основными разделами прикладной математики, которые находят наибольшее применение при решении базовых задач, связанных с управлением и проектированием электроэнергетических систем. Это позволяет связать математику как общетеоретическую науку с ее применением в инженерной практике и научных исследованиях, сформировать грамотный технический подход к решению инженерных и научных проблем, а также подготовить студента к более глубокому и критическому восприятию специальных дисциплин.
В курсе “Математические задачи электроэнергетики” будут представлены основные научные достижения в области управления таким сложным объектом как электроэнергетическая система (ЭЭС), рассмотрены возможности современной математики и вычислительной техники, позволяющие смоделировать реальные процессы, происходящие в ЭЭС.
В пособии представлены программа курса с ссылками на литературу, задание на выполнение контрольной работы для студентов заочного отделения, методические указания для проведения расчетов вручную и с использованием ЭВМ. Материал, изложенный в пособии может быть использован также студентами дневного отделения ФЭН при подготовке в практическим занятиям по курсу.
ПРОГРАММА КУРСА.
Техническая постановка задачи расчета и анализа
Установившихся режимов электрических систем.
Электрическая система (ЭС) как объект математического моделирования. Понятие режима работы ЭС. Виды режимов. Параметры режима функционирования ЭС. Общая характеристика разделов прикладной математики, используемых при решении задачи расчета установившихся режимов ЭС ([1]с.7-30,[2]c.5 — 6).
Уравнения состояния электрических систем
1.2.1 Понятие схемы замещения электрической системы. Схемы замещения источников энергии, потребителей и элементов электрической сети. Пример перехода от реальной схемы электрической системы к схеме замещения. Моделирование электрической сети с помощью направленного графа ([1]c.31-33,37-38,[2]c.6-10,[3]c.109-111).
1.2.2. Использование матричных методов прикладной математики для моделирования процессов, происходящих в электрической системе. Основы матричной алгебры. Действия с матрицами. Виды матриц, используемых при расчете установившихся режимов. Матрицы инциденций первого и второго рода. Правила формирования матриц инциденций, исходя из структуры электрической сети, представленной в виде графа. Матрицы режимных параметров ([5]c.35-52,[1]c.38-40,[2]c.10-13,[3]c.114-118).
1.2.3 Виды уравнений состояния электрической системы. Представление в матричной форме основных законов электротехники: закона Ома, первого и второго законов Кирхгофа. Получение обобщенного уравнения состояния на основе двух законов Кирхгофа. Уравнения узловых напряжений. Структура и физический смысл элементов матрицы узловых проводимостей. Контурные уравнения состояния ЭС. Преимущества и недостатки различных форм представления уравнений состояния с учетом удобства реализации алгоритмов на ЭВМ ([1] c.40-42, c.48-56, [2] c.13-30, [3] c.118-129,[4]c.25-35).
Методы решения уравнений состояния электрических систем.
1.3.1. Математическая модель задачи расчета и анализа установившихся режимов ЭС. Способы представления параметров генераторных и нагрузочных узлов схемы замещения электрической системы. Классификация методов решения систем уравнений состояния ([1]c.70-74,[2]c.30-33, [4]c.8-14,c.35)
1.3.2. Характеристика прямых методов решения уравнений состояния, представленных в виде систем линейных алгебраических уравнений. Алгоритм метода Гаусса с обратным ходом и без обратного хода. Анализ точности полученного решения по сумме невязок. Факторы, влияющие на точность решения систем уравнений методом Гаусса. Применение метода Гаусса для решения системы линейных уравнений узловых напряжений.([1] c.79-88, [2] c.34-36, [4] c.35-39).
1.3.3. Общая характеристика итерационных методов решения систем уравнений. Понятие итерационного процесса. Виды итерационных процессов. Критерии сходимости итерационных процессов. Метод простой итерации. Метод Зейделя и его применение для решения систем линейных уравнений узловых напряжений. Сравнительная характеристика итерационных методов с учетом их реализации на ЭВМ ([1] c.91-101, [2]c.37-38,[4] c.43-50).
1.3.4. Нелинейные уравнения установившегося режима. Представление нелинейных уравнений состояния в форме баланса токов и в форме баланса мощностей. Использование метода Зейделя для решения систем нелинейных уравнений состояния. Метод Ньютона. Графическая интерпретация метода Ньютона для функции одной переменной. Алгоритм метода Ньютона для функции многих переменных([4]c.57-60,c.64-76).
Видео:Матричный метод решения систем уравненийСкачать

Уравнения Колмогорова.
Предельные вероятности состояний
Рассмотрим математическое описание марковского процесса с дискретными состояниями и непрерывным временем* на примере случайного процесса из примера 1, граф которого изображен на рис. 1. Будем полагать, что все переходы системы из состояния в происходят под воздействием простейших потоков событий с интенсивностями ; так, переход системы из состояния в будет происходить под воздействием потока отказов первого узла, а обратный переход из состояния в — под воздействием потока «окончаний ремонтов» первого узла и т.п.
Граф состояний системы с проставленными у стрелок интенсивностями будем называть размеченным (см. рис. 1). Рассматриваемая система имеет четыре возможных состояния: .
Вероятностью i-го состояния называется вероятность того, что в момент система будет находиться в состоянии . Очевидно, что для любого момента сумма вероятностей всех состояний равна единице:
Рассмотрим систему в момент и, задав малый промежуток , найдем вероятность того, что система в момент будет находиться в состоянии . Это достигается разными способами.
1. Система в момент с вероятностью находилась в состоянии , а за время не вышла из него.
Вывести систему из этого состояния (см. граф на рис. 1) можно суммарным простейшим потоком с интенсивностью , т.е. в соответствии с формулой (7), с вероятностью, приближенно равной . А вероятность того, что система не выйдет из состояния , равна . Вероятность того, что система будет находиться в состоянии по первому способу (т.е. того, что находилась в состоянии и не выйдет из него за время ), равна по теореме умножения вероятностей:
2. Система в момент с вероятностями (или ) находилась в состоянии или и за время перешла в состояние .
Потоком интенсивностью (или — с- рис. 1) система перейдет в состояние с вероятностью, приближенно равной (или ). Вероятность того, что система будет находиться в состоянии по этому способу, равна (или ).
Применяя теорему сложения вероятностей, получим
Переходя к пределу при (приближенные равенства, связанные с применением формулы (7), перейдут в точные), получим в левой части уравнения производную (обозначим ее для простоты ):
Получили дифференциальное уравнение первого порядка, т.е. уравнение, содержащее как саму неизвестную функцию, так и ее производную первого порядка.
Рассуждая аналогично для других состояний системы , можно получить систему дифференциальных уравнений Колмогорова для вероятностей состояний:
Сформулируем правило составления уравнений Колмогорова . В левой части каждого из них стоит производная вероятности i-го состояния. В правой части — сумма произведений вероятностей всех состояний (из которых идут стрелки в данное состояние) на интенсивности соответствующих потоков событий, минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность данного (i-го состояния).
В системе (9) независимых уравнений на единицу меньше общего числа уравнений. Поэтому для решения системы необходимо добавить уравнение (8).
Особенность решения дифференциальных уравнений вообще состоит в том, что требуется задать так называемые начальные условия, т.е. в данном случае вероятности состояний системы в начальный момент . Так, например, систему уравнений (9) естественно решать при условии, что в начальный момент оба узла исправны и система находилась в состоянии , т.е. при начальных условиях .
Уравнения Колмогорова дают возможность найти все вероятности состояний как функции времени . Особый интерес представляют вероятности системы в предельном стационарном режиме , т.е. при , которые называются предельными (или финальными) вероятностями состояний.
В теории случайных процессов доказывается, что если число состояний системы конечно и из каждого из них можно (за конечное число шагов) перейти в любое другое состояние, то предельные вероятности существуют.
Предельная вероятность состояния имеет четкий смысл: она показывает среднее относительное время пребывания системы в этом состоянии . Например, если предельная вероятность состояния , т.е. , то это означает, что в среднем половину времени система находится в состоянии .
Так как предельные вероятности постоянны, то, заменяя в уравнениях Колмогорова их производные нулевыми значениями, получим систему линейных алгебраических уравнений, описывающих стационарный режим. Для системы с графом состояний, изображенном на рис. 1), такая система уравнений имеет вид:
Систему (10) можно составить непосредственно по размеченному графу состояний, если руководствоваться правилом , согласно которому слева в уравнениях стоит предельная вероятность данного состояния , умноженная на суммарную интенсивность всех потоков, ведущих из данного состояния, а справа — сумма произведений интенсивностей всех потоков, входящих в i-е состояние, на вероятности тех состояний, из которых эти потоки исходят.
Пример 2. Найти предельные вероятности для системы из примера 1, граф состояний которой приведен на рис. 1, при
Решение. Система алгебраических уравнений, описывающих стационарный режим для данной системы, имеет вид (10) или
(Здесь мы вместо одного «лишнего» уравнения системы (10) записали нормировочное условие (8)).
Решив систему (11), получим , т.е. в предельном, стационарном режиме система в среднем 40% времени будет находиться в состоянии (оба узла исправны), 20% — в состоянии (первый узел ремонтируется, второй работает), 27% — в состоянии (второй узел ремонтируется, первый работает) и 13% времени — в состоянии (оба узла ремонтируются)
Пример 3. Найти средний чистый доход от эксплуатации в стационарном режиме системы в условиях примеров 1 и 2, если известно, что в единицу времени исправная работа первого и второго узлов приносит доход соответственно в 10 и 6 ден.ед., а их ремонт требует затрат соответственно в 4 и 2 ден.ед. Оценить экономическую эффективность имеющейся возможности уменьшения вдвое среднего времени ремонта каждого из двух узлов, если при этом придется вдвое увеличить затраты на ремонт каждого узла (в единицу времени).
Решение. Из примера 2 следует, что в среднем первый узел исправно работает долю времени, равную , а второй узел — . В то же время первый узел находится в ремонте в среднем долю времени, равную , а второй узел — . Поэтому средний чистый доход в единицу времени от эксплуатации системы, т.е. разность между доходами и затратами, равен
Уменьшение вдвое среднего времени ремонта каждого из узлов в соответствии с (6) будет означать увеличение вдвое интенсивностей потока «окончаний ремонтов» каждого узла, т.е. теперь и система линейных алгебраических уравнений (10), описывающая стационарный режим системы , вместе с нормировочным условием (8) примет вид:
Решив систему, получим .
Учитывая, что , а затраты на ремонт первого и второго узла составляют теперь соответственно 8 и 4 ден.ед., вычислим средний чистый доход в единицу времени:
Так как больше (примерно на 20%), то экономическая целесообразность ускорения ремонтов узлов очевидна.
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Процесс гибели и размножения
В теории массового обслуживания широкое распространение имеет специальный класс случайных процессов — так называемый процесс гибели и размножения . Название этого процесса связано с рядом биологических задач, где он является математической моделью изменения численности биологических популяций.
Граф состояний процесса гибели и размножения имеет вид, показанный на рис. 4.
Рассмотрим упорядоченное множество состояний системы . Переходы могут осуществляться из любого состояния только в состояния с соседними номерами, т.е. из состояния возможны переходы только либо в состояние , либо в состояние .
Предположим, что все потоки событий, переводящие систему по стрелкам графа, простейшие с соответствующими интенсивностями или .
По графу, представленному на рис. 4, составим и решим алгебраические уравнения для предельных вероятностей состояний (их существование вытекает из возможности перехода из каждого состояния в каждое другое и конечности числа состояний).
В соответствии с правилом составления таких уравнений (см. 13) получим: для состояния
для состояния имеем , которое с учетом (12) приводится к виду
Аналогично, записывая уравнения для предельных вероятностей других состояний, можно получить следующую систему уравнений:
к которой добавляется нормировочное условие
При анализе численности популяций считают, что состояние соответствует численности популяции, равной , и переход системы из состояния в состояние происходит при рождении одного члена популяции, а переход в состояние — при гибели одного члена популяции.
Решая систему (14), (15), можно получить
Легко заметить, что в формулах (17) для коэффициенты при есть слагаемые, стоящие после единицы в формуле (16). Числители этих коэффициентов представляют произведение всех интенсивностей, стоящих у стрелок, ведущих слева направо до данного состояния , а знаменатели — произведение всех интенсивностей, стоящих у стрелок, ведущих справа налево до состояния .
Пример 4. Процесс гибели и размножения представлен графом (рис. 5). Найти предельные вероятности состояний.
🔥 Видео
Решение систем уравнений методом подстановкиСкачать

Решение системы уравнений методом Крамера.Скачать

Решение систем уравнений методом сложенияСкачать

Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Решение системы уравнений методом ГауссаСкачать

Решение систем уравнений второго порядка. 8 класс.Скачать

Решение систем уравнений методом сложенияСкачать

ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод ПодстановкиСкачать

Способы решения систем нелинейных уравнений. 9 класс.Скачать

МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

Графический способ решения систем уравнений. Алгебра, 9 классСкачать

6 способов в одном видеоСкачать

Решение системы уравнений методом обратной матрицы - bezbotvyСкачать

Решение систем уравнений. Методом подстановки. Выразить YСкачать

Система линейных уравнений. Метод обратной матрицы. Матричный метод.Скачать

Методы решения систем уравнений. Видеоурок по алгебре 9 классСкачать

Решение системы линейных уравнений графическим методом. 7 класс.Скачать