Логарифмическим уравнениям и неравенствам в вариантах ЕГЭ по математике посвящена задача C3. Научиться решать задания C3 из ЕГЭ по математике должен каждый ученик, если он хочет сдать предстоящий экзамен на «хорошо» или «отлично». В данной статье представлен краткий обзор часто встречающихся логарифмических уравнений и неравенств, а также основных методов их решения.
Итак, разберем сегодня несколько примеров логарифмических уравнений и неравенств, которые предлагались учащимся в вариантах ЕГЭ по математике прошлых лет. Но начнет с краткого изложение основных теоретических моментов, которые нам понадобятся для их решения.
- Логарифмическая функция
- Определение
- Основные свойства
- Решение логарифмических уравнений и неравенств
- Алгебра
- Уравнения вида logaf(x) = logag(x)
- Уравнения, требующие предварительных преобразований
- Логарифмические уравнения с заменой переменных
- Логарифмирование уравнений
- Переход от логарифмических неравенств к нелогарифмическим
- Логарифмические уравнения и системы
- п.1. Методы решения логарифмических уравнений
- п.2. Решение уравнений вида (log_a f(x)=log_a g(x))
- п.3. Решение уравнений вида (log_ f(x)=log_ g(x)) Как и в предыдущем случае, можно сначала найти ОДЗ, а потом решать уравнение. Или же, можно решить уравнение, а потом проверить требования ОДЗ прямой подстановкой полученных корней. Например: Решим уравнение (log_(x^2-4)=log_(2-x)) Найдем ОДЗ в явном виде: ( begin x^2-4gt 0\ 2-xgt 0\ x+5gt 0\ x+5ne 1 end Rightarrow begin xlt -2cup xgt 2\ xlt 2\ xgt -5\ xne -4 end Rightarrow begin -5lt xlt -2\ xne -4 end Rightarrow xin (-5;-4)cup(-4;-2) ) Решаем уравнение: (x^2-4=2-x) (x^2+x-6=0) ((x+3)(x-2)=0) ( left[ begin x_1=-3\ x_2=2 — text end right. ) Ответ: -3 В логарифмическом уравнении перед отбрасыванием логарифмов основания обязательно должны быть равны. Не забывайте это проверять! Например: Решим уравнение (log_(x+1)=log_(x+3)) Основания (2ne 4), и нельзя сразу написать (x+1=x+3). Нужно привести к одному основанию, преобразовав левую часть: (log_2(x+1)=log_(x+1)^2=log_4(x+1)^2) Тогда исходное уравнение примет вид: (log_4(x+1)^2=log_4(x+3)) И теперь: ((x+1)^2=x+3) (x^2+x-2=0) ((x+2)(x-1)=0) ( left[ begin x_1=-2\ x_2=1 end right. ) Что касается ОДЗ, то её нужно искать для исходного уравнения: ( begin x+1gt 0\ x+3gt 0 end Rightarrow begin xgt -1\ xgt -3 end Rightarrow xgt -1 ) Корень (x_1=-2lt -1) — не подходит. Ответ: 1 Преобразования могут расширить первоначальную область допустимых значений (например, при возведении в квадрат), и вы включите в решение лишние корни. Преобразования также могут сузить ОДЗ (например, при взятии корня), и некоторые решения окажутся потеряны. Поэтому ОДЗ определяется для исходного уравнения (выражения, неравенства), а не того, которое получено после преобразований. п.4. Примеры Пример 1. Решите уравнения: a) ( log_2(x+1)-log_2(x-1)=1 ) ОДЗ: ( begin x+1gt 0\ x-1gt 0 end Rightarrow begin xgt -1\ xgt 1 end Rightarrow xgt 1 ) (log_2left((x+1)(x-1)right)=log_22) (x^2-1=2Rightarrow x^2 =3) ( left[ begin x_1=-sqrtlt 2 — text\ x_2=sqrt end right. ) Ответ: (sqrt) б) ( 2log_5(x-1)=log_5(1,5x+1) ) ОДЗ: ( begin x-1gt 0\ 1,5x+1gt 0 end Rightarrow begin xgt 1\ xgt-frac23 end Rightarrow xgt 1 ) Преобразуем: (2log_5(x-1)=log_5(x-1)^2) Получаем: (log_5(x-1)^2=log_5(1,5x+1)) ((x-1)^2=1,5x+1) (x^2-2x+1-1,5x-1=0Rightarrow x^2-3,5x=0Rightarrow x(x-3,5)=0) ( left[ begin x_1=0lt 1 — text\ x_2=3,5 end right. ) Ответ: 3,5 в) ( log_3(3-x)+log_3(4-x)=1+2log_3 2 ) ОДЗ: ( begin 3-xgt 0\ 4-xgt 0 end Rightarrow begin xlt 3\ xlt 4 end Rightarrow xlt 3 ) Преобразуем: (1+2log_3 2=log_3 3+log_3 2^2=log_3(3cdot 4)=log_3 12) Получаем: (log_3left((3-x)(4-x)right)=log_3 12) ((3-x)(4-x)=12Rightarrow 12-7x+x^2=12Rightarrow x(x-7)=0) ( left[ begin x_1=0\ x_2=7gt 3 — text end right. ) Ответ: 0 г) ( log_2^2x+log_2 x^2+1=0 ) ОДЗ: (xgt 0) (log_2x^2=2log_2x) Получаем: (log_2^2x+2log_2x+1=0) Замена: (t=log_2 x) (t^2+2t+1=0Rightarrow(t+1)^2=0Rightarrow t=-1) Возвращаемся к исходной переменной: (log_2x=-1) (x=2^=frac12) Ответ: (frac12) д) ( x^=10 ) ОДЗ: (xgt 0) Замена: (t=lg x). Тогда (x=10^t) Подставляем: ((10^t)^t=10Rightarrow 10^=10^1Rightarrow t^2=1Rightarrow t=pm 1) Возвращаемся к исходной переменной: ( left[ begin lg x=-1\ lg x=1 end right. Rightarrow left[ begin x=10^\ x=10 end right. Rightarrow left[ begin x_1=0,1\ x_2=10 end right. ) Оба корня подходят. Ответ: e) ( sqrtcdot log_5(x+3)=0 ) ОДЗ: ( begin xgeq 0\ x+3gt 0 end Rightarrow begin xgeq 0\ xgt -3 end Rightarrow xgeq 0 ) ( left[ begin sqrt=0\ log_5(x+3)=0 end right. Rightarrow left[ begin x=0\ x+3=5^0=1 end right. Rightarrow left[ begin x_1=0\ x_2=-2lt 0 — text end right. ) Ответ: 0 ж) ( log_2+2log_x=log_(x+1) ) ОДЗ: ( begin xgt 0\ x+1gt 0\ 5x-2gt 0\ 5x-2ne 1 end Rightarrow begin xgt 0\ xgt -1\ xgtfrac25\ xnefrac35 end Rightarrow begin xgtfrac25\ xnefrac35 end ) Преобразуем: (log_2+2log_x=log_(2x^2)) Подставляем: (log_(2x^2)=log_(x+1)) ( 2x^2=x+1Rightarrow 2x^2-x-1=0Rightarrow (2x+1)(x-1)=0 Rightarrow left[ begin x_1=-frac12 — text\ x_2=1 end right. ) Ответ: 1 Пример 2*. Решите уравнения: a) ( log_4log_2log_3(2x-1)=frac12 ) ОДЗ: ( begin 2x-1gt 0\ log_3(2x-1)gt 0\ log_2log_3(2x-1)gt 0 end Rightarrow begin xgtfrac12\ 2x-1gt 3^0\ log_3(2x-1)gt 2^0 end Rightarrow begin xgtfrac12\ xgt 1\ 2x-1gt 3^1 end Rightarrow ) ( Rightarrow begin xgtfrac12\ xgt 1\ xgt 2 end Rightarrow xgt 2 ) Решаем: (log_2log_3(2x-1)=4^=2) (log_3(2x-1)=2^2=4) (2x-1=3^4=81) (2x=82) (x=41) Ответ: 41 б) ( log_2(9-2^x)=25^<log_5sqrt> ) ОДЗ: ( begin 9-2xgt 0\ 3-xgt 0 end Rightarrow begin 2^xlt 9\ xlt 3 end Rightarrow begin xltlog_2 9\ xlt 3 end Rightarrow xlt 3 ) Преобразуем: (25^<log_5sqrt>=25^<log_(sqrt)^2>=25^<log_(3-x)>=3-x) Подставляем: (log_2(9-2^x)=3-x) (9-2^x=2^) (9-2^x-frac=0) Замена: (t=2^xgt 0) ( 9-t-frac8t=0Rightarrow frac=0Rightarrow begin t^2-9t+8gt 0\ tne 0 end Rightarrow begin (t-1)(t-8)=0\ tne 0 end Rightarrow left[ begin t_1=1\ t_2=8 end right. ) Возвращаемся к исходной переменной: ( left[ begin 2^x=1\ 2^x=8 end right. Rightarrow left[ begin 2^x=2^0\ 2^x=2^3 end right. Rightarrow left[ begin x_1=0\ x_2=3 end right. ) По ОДЗ (xlt 3), второй корень не подходит. Ответ: 0 в) ( lgsqrt+lgsqrt+1=lg 30 ) ОДЗ: ( begin x-5gt 0\ 2x-3gt 0 end Rightarrow begin xgt 5\ xgtfrac32 end Rightarrow xgt 5 ) Преобразуем: (lg 30-1=lg 30-lg 10=lgfrac=lg 3) Подставляем: (lgsqrt+lgsqrt=lg 3) (frac12lg(x-5)+frac12lg(2x-3)=lg 3 |cdot 2) (lg(x-4)+lg(2x-3)=2lg 3) (lgleft((x-5)(2x-3)right)=lg 3^2) ((x-5)(2x-3)=9Rightarrow 2x^2-13x+15-9=0 Rightarrow 2x^2-13x+6=0) ( (2x-1)(x-6)=0Rightarrow left[ begin x_1=frac12lt 5 — text\ x_2=6 end right. ) Ответ: 6 г) ( frac+frac+frac=0 ) ОДЗ: ( begin xgt 0\ lg xne 0\ lg 10xne 0\ lg 100xne 0 end Rightarrow begin xgt 0\ xne 1\ 10xne 1\ 100xne 1 end Rightarrow begin xgt 0\ xneleft<frac;frac;1right> end ) Преобразуем: (lg 10x=lg 10+lg x=1+lg 10) (lg 100x=lg 100+lg x=2+lg x) Подставляем: (frac+frac+frac=0) Замена: (t=lg x) begin frac1t+frac+frac=0Rightarrow frac1t+frac=-fracRightarrow frac=-fracRightarrow (1+2t)(2+t)=(1+t)\ 2_5t+2t^2=-3t-3t^2Rightarrow 5t^2+8t+2=0\ D=8^2-4cdot 5cdot 2=24, t=frac<-8pm 2sqrt>=frac<-4pm sqrt> end Возвращаемся к исходной переменной: $$ left[ begin lg x=frac<-4- sqrt>\ lg x=frac<-4+ sqrt> end right. Rightarrow left[ begin x=10frac<-4- sqrt>\ x=10frac<-4+ sqrt> end right. $$ Оба корня подходят. Ответ: (left<10frac<-4pmsqrt>right>) e) ( x^<frac>=10^ ) ОДЗ: (xgt 0) Замена: (t=lg x.) Тогда (x=10^t) Подставляем: begin (10^t)^<frac>=10^\ frac=t+1Rightarrow t(t+7)=4(t+1)Rightarrow t^2+7t-4t-4=0\ t^2+3t-4=0Rightarrow (t+4)(t-1)=0Rightarrow left[ begin t_1=-4\ t_2=1 end right. end Возвращаемся к исходной переменной: $$ left[ begin lg x=-4\ lg x=1 end right. Rightarrow left[ begin x=10^\ x=10 end right. Rightarrow left[ begin x_1=0,0001\ x_2=10 end right. $$ Оба корня подходят. Ответ: (left) ж) ( 4^=(2x^2+2x+5)^ ) ОДЗ: ( begin 1-xgt 0\ 2x^2+2x+5gt 0 end Rightarrow begin xlt 1\ Dlt 0, xinmathbb end Rightarrow xlt 1 ) По условию: begin log_3(1-x)=log_4left((2x^2+2x+5)^right)\ log_3(1-x)=log_32cdotlog_4(2x^2+2x+5) end Перейдем к другому основанию: $$ frac=fraccdotfrac |cdot lg 3 $$ (frac=frac=frac=frac12) begin lg(1-x)=frac12cdotlg(2x^2+2x+5) |cdot 2\ 2lg(1-x)=lg(2x^2+2x+5)\ lg(1-x)^2=lg(2x^2+2x+5)\ (1-x)^2=2x^2+2x+5\ 1-2x+x^2=2x^2+2x+5\ x^2+4x+4=0\ (x+2)^2=0\ x=-2 end Ответ: -2 Пример 3. Решите систему уравнений: a) ( begin lg x+lg y=lg 2\ x^2+y^2=5 end ) ОДЗ: ( begin xgt 0\ ygt 0 end ) Из первого уравнения: (lg(xy)=lg 2Rightarrow xy=2) Получаем: ( begin xy=2\ x^2+y^2=5 end Rightarrow begin y=frac2x\ x^2+left(frac2xright)^2-5=0 end ) Решаем биквадратное уравнение: begin x^2+frac-5=0Rightarrowfrac=0Rightarrow begin x^4-5x^2+4=0\ xne 0 end \ (x^2-4)(x^2-1)=0Rightarrow left[ begin x^2=4\ x^2=1 end right. Rightarrow left[ begin x=pm 2\ x=pm 1 end right. end Согласно ОДЗ, оставляем только положительные корни. Получаем две пары решений: ( left[ begin begin x=1\ y=frac2x=2 end \ begin x=2\ y=frac22=1 end end right. ) Ответ: (left) б) ( begin x^=27\ x^=frac13 end ) ОДЗ: (xgt 0, xne 1) Логарифмируем: ( begin y+1=log_x27=log_x3^3=3log_x3\ 2y-5=log_xfrac13=log_x3^=-log_x3 end ) Замена: (z=log_x3) begin begin y+1=3z\ 2y-5=-z |cdot 3 end Rightarrow begin y+1=3z\ 6y-15=-3z end Rightarrow begin 7y-14=0\ z=5-2y end Rightarrow begin y=2\ z=1 end end Возвращаемся к исходной переменной: $$ begin y=2\ log_x3=1 end Rightarrow begin x^1=3\ y=2 end Rightarrow begin x=3\ y=2 end $$ Ответ: (3;2) в*) ( begin 3(log_y x-log_x y)=8\ xy=16 end ) ОДЗ: ( begin xgt 0, xne 1\ ygt 0, yne 1 end ) Сделаем замену (t=log_x y). Тогда (log_y x=frac=frac1t) Подставим в первое уравнение и решим его: begin 3left(frac1t-tright)=8Rightarrowfrac=frac83Rightarrow begin 3(1-t^2)=8t\ tne 0 end\ 3t^2+8t-3=0Rightarrow (3t-1)(t+3)=0Rightarrow left[ begin t_1=frac13\ t_2=-3 end right. end Прологарифмируем второе уравнение по (x): $$ log_x(xy)=log_x16Rightarrow 1+log_x y=log_x16Rightarrow 1+t=log_x 16 $$ Получаем: begin left[ begin begin t=frac13\ log_x16=1+t=frac43 end \ begin t=-3\ log_x16=1+t=-2 end end right. Rightarrow left[ begin begin t=frac13\ x^=16 end \ begin t=-3\ x^=16 end end right. Rightarrow left[ begin begin t=frac13\ x=(2^4)^=2^3=8 end \ begin t=-3\ x=(16)^=frac14 end end right. end Возвращаемся к исходной переменной: begin left[ begin begin x=8\ log_x y=frac13 end \ begin x=frac14\ log_x y=-3 end end right. Rightarrow left[ begin begin x=8\ y=8^=2 end \ begin x=frac14\ y=left(frac14right)^=64 end end right. end Ответ: (left) г*) ( begin (x+y)cdot 3^=frac\ 3log_5(x+y)=x-y end ) ОДЗ: (x+ygt 0) Прологарифмируем первое уравнение по 3: begin log_3left((x+y)cdot 3^right)=log_3frac\ log_3(x+y)+(y-x)=log_3frac\ log_3(x+y)-log_3frac=x-y end Получаем:(x-y=3log_5(x+y)=log_3(x+y)-log_3frac) Решим последнее уравнение относительно (t=x+y) begin 3log_5 t=log_3 t-log_3frac\ 3cdotfrac-log_3t=-log_3frac\ log_3tcdotleft(frac-1right)=-log_3frac\ log_3t=-frac<log_3frac><frac-1>=-frac=log_35\ t=5 end Тогда: (x-y=3log_5t=3log_55=3) Получаем систему линейных уравнений: begin begin x+y=5\ x-y=3 end Rightarrow begin 2x=5+3\ 2y=5-3 end Rightarrow begin x=4\ y=1 end end Требование ОДЗ (x+y=4+1gt 0) выполняется. Ответ: (4;1)
- п.4. Примеры
- 📸 Видео
Видео:✓ Как решать логарифмические уравнения и неравенства, не помня свойства логарифмов | Борис ТрушинСкачать

Логарифмическая функция
Определение
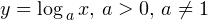
называют логарифмической функцией.
Основные свойства
Основные свойства логарифмической функции y = loga x:
| | a > 1 | 0 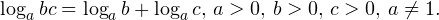 0,, b>0,, c>0,, ane 1. ]» title=»Rendered by QuickLaTeX.com»/> 0,, b>0,, c>0,, ane 1. ]» title=»Rendered by QuickLaTeX.com»/>• Логарифм частного двух положительных чисел равен разности логарифмов этих чисел:
• Если a и b — положительные числа, причем a ≠ 1, то для любого числа r справедливо равенство:
• Если a, b, c — положительные числа, причем a и c отличны от единицы, то имеет место равенство (формула перехода к новому основанию логарифма):
Видео:84 людей этого не знают! Секретный способ решения Логарифмических УравненийСкачать  Решение логарифмических уравнений и неравенствПример 1. Решите уравнение: Решение. В область допустимых значений входят только те x, при которых выражение, находящееся под знаком логарифма, больше нуля. Эти значения определяются следующей системой неравенств:
С учетом того, что получаем промежуток, определяющий область допустимых значений данного логарифмического уравнения: На основании теоремы 1, все условия которой здесь выполнены, переходим к следующему равносильному квадратичному уравнению: В область допустимых значений входит только первый корень. Ответ: x = 7. Пример 2. Решите уравнение: Решение. Область допустимых значений уравнения определяется системой неравенств:
Очевидно, что эти два условия противоречат друг другу. То есть нет ни одного такого значения x, при котором одновременно выполнялись бы оба неравенства. Область допустимых значений уравнения является пустым множеством, а значит решений у данного логарифмического уравнения нет. Ответ: корней нет. Обратите внимание, что в этом задании нам вообще не пришлось искать корни уравнения. Достаточно оказалось определить, что его область допустимых значений не содержит ни одного действительно числа. Это одно из преимуществ такой последовательности решения логарифмических уравнений и неравенств (начинать с определения области допустимых значений уравнения, а затем решать его путем равносильных преобразований). Примет 3. Решите уравнение: Решение. Область допустимых значений уравнения определяется здесь легко: x > 0. Уравнение принимает вид: Оба ответа входят в область допустимых значений уравнения, поскольку являются положительными числами. Пример 4. Решите уравнение: Решение. Вновь начнем решение с определения области допустимых значений уравнения. Она определяется следующей системой неравенств:
Воспользовавшись правилом сложения логарифмов, переходим к равносильному в области допустимых значений уравнению: Основания логарифмов одинаковы, поэтому в области допустимых значений можно перейти к следующему квадратному уравнению: Первый корень не входит в область допустимых значений уравнения, второй — входит. Ответ: x = -1. Пример 5. Решите уравнение: Решение. Будем искать решения в промежутке x > 0, x≠1. Преобразуем уравнение к равносильному: Оба ответа входят в область допустимых значений уравнения. Пример 6. Решите уравнение: Решение. Система неравенств, определяющая область допустимых значений уравнения, имеет на этот раз вид: Используя свойства логарифма, преобразуем уравнение к равносильному в области допустимых значений уравнению: Используя формулу перехода к новому основанию логарифма, получаем: В область допустимых значений входит только один ответ: x = 4. Перейдем теперь к логарифмическим неравенствам. Это как раз то, с чем вам придется иметь дело на ЕГЭ по математике. Для решения дальнейших примеров нам потребуется следующая теорема: Теорема 2. Если f(x) > 0 и g(x) > 0, то: Решение. Начнем с определения области допустимых значений неравенства. Выражение, стоящее под знаком логарифмической функции, должно принимать только положительные значения. Это значит, что искомая область допустимых значений определяется следующей системой неравенств:
Так как в основании логарифма стоит число, меньшее единицы, соответствующая логарифмическая функция будет убывающей, а потому равносильным по теореме 2 будет переход к следующему квадратичному неравенству: Окончательно, с учетом области допустимых значений получаем ответ: Пример 8. Решите неравенство: Решение. Вновь начнем с определения области допустимых значений:
На множестве допустимых значений неравенства проводим равносильные преобразования: После сокращения и перехода к равносильному по теореме 2 неравенству получаем: С учетом области допустимых значений получаем окончательный ответ: Пример 9. Решите логарифмическое неравенство: Решение. Область допустимых значений неравенства определяется следующей системой:
Видно, что в области допустимых значений выражение, стоящее в основании логарифма, всегда больше единицы, а потому равносильным по теореме 2 будет переход к следующему неравенству: С учетом области допустимых значений получаем окончательный ответ: Пример 10. Решите неравенство: Решение. Область допустимых значений неравенства определяется системой неравенств:
I способ. Воспользуемся формулой перехода к новому основанию логарифма и перейдем к равносильному в области допустимых значений неравенству: Неравенство будет равносильно двум системам. Первой: Итак, окончательный ответ: II способ. Решаем методом интервалов. Преобразуем неравенство к виду: Вычтем из знаменателя С учетом того, что выражения Множество решений данного неравенства Итак, Итак, что нужно для того, чтобы решать логарифмические уравнения и неравенства?
Главное же требование — это настойчивость в достижении своей цели. Учитесь, тренируйтесь, если нужно — ежедневно, изучайте и запоминайте на примерах основные способы решения неравенств и их систем, анализируйте возникающие ошибки и не допускайте их в будущем. За помощью в этом нелегком деле вы можете обратиться к своему школьному учителю по математике, репетитору, родителям, друзьям и знакомым, книгам, а также огромному количеству материалов, доступных на просторах Интернета. Желаю вам успехов в подготовке к Единому государственному экзамену по математике. Видео:Решение логарифмических уравнений #shortsСкачать  АлгебраПлан урока: Задание. Укажите корень логарифмического уравнения Задание. Решите урав-ние В чуть более сложных случаях под знаком логарифма может стоять не сама переменная х, а выражение с переменной. То есть урав-ние имеет вид Задание. Найдите решение логарифмического уравнения Задание. Решите урав-ние Задание. Решите урав-ние Получили показательное уравнение. Показатели степеней можно приравнять, если равны их основания: Видео:Логарифмические уравнения. 11 класс.Скачать  Уравнения вида logaf(x) = logag(x)Порою логарифм стоит в обеих частях равенства, то есть и слева, и справа от знака «равно». Если основания логарифмов совпадают, то должны совпадать и аргументы логарифмов. Задание. Решите урав-ние Задание. Найдите корень урав-ния Ситуация несколько усложняется в том случае, когда, под знаком логарифма в обоих частях равенства стоят выражения с переменными, то есть оно имеет вид С одной стороны, очевидно, что должно выполняться равенство f(x) = g(x). Но этого мало, ведь под знаком логарифма не должно стоять отрицательное число. Поэтому после получения корней следует подставить их в урав-ние и убедиться, что они не являются посторонними корнями. Задание. Решите урав-ние Получили квадратное уравнение, которое решаем с помощью дискриминанта: Получили два корня, (– 3) и 4. Однако теперь подставим их в исходное урав-ние и посмотрим, что у нас получится. При х = – 3 имеем: Это верное равенство, поэтому х = – 3 действительно является корнем урав-ния. Теперь проверяем х = 4: Хотя выражения и справа, и слева одинаковы, равенство верным считать нельзя, ведь выражение log3 (– 1) не имеет смысла! Действительно, нельзя вычислять логарифм от отрицательного числа. Поэтому корень х = 4 оказывается посторонним, и у нас остается только один настоящий корень – число (– 3). Видео:11 класс, 18 урок, Логарифмические неравенстваСкачать  Уравнения, требующие предварительных преобразованийЕстественно, не всегда в обоих частях логарифмических уравнений и неравенств стоят только логарифмы с совпадающими основаниями. Часто требуется выполнить некоторые предварительные преобразования, чтобы привести урав-ние к виду logaf(x) = logag(x). Задание. Решите урав-ние с помощью которой любой множитель можно внести под знак логарифма. Сделаем это и в нашем случае: Теперь в обеих частях равенства не стоит ничего, кроме логарифмов с одинаковыми основаниями. Поэтому мы можем приравнять их аргументы: Задание. Решите урав-ние Снова проверяем каждый из корней, подставляя его в исходное ур-ние. Прих = –1 получаем Задание. Решите урав-ние Решение. В правой части снова стоит сумма, но на этот раз не логарифмов. Однако число 1 можно представить как log5 5. Тогда урав-ние можно преобразовать: Задание. Решите урав-ние Решение. Данный пример похож на простейшее логарифмическое уравнение, однако переменная находится в основании логарифма, а не в аргументе. По определению логарифма мы можем записать, что Первый вариант придется отбросить, так как основание логарифма, (а в данном случае это выражение х – 5) не может быть отрицательным числом. Получается, что Задание. Решите урав-ние Решение. Здесь ситуация осложняется тем, что основания логарифмов разные. Поэтому один из них необходимо привести к новому основанию. Попробуем привести log25x 4 к основанию 5, используя известную нам формулу Мы добились того, что у логарифмов одинаковые основания, а потому мы можем приравнять их аргументы: Видео:Методы решения логарифмических уравненийСкачать  Логарифмические уравнения с заменой переменныхИногда приходится делать некоторые замены, чтобы уравнение приняло более привычный вид. Задание. Решите уравнение методом замены переменной Задание. Найдите решение уравнения методом замены переменной Решение. Для начала напомним, что символ lg означает десятичный логарифм. Отдельно знаменатель дроби в правой части: Видео:Круговорот воды в природе ➜ Решение логарифмических уравнений из ЕГЭ #ShortsСкачать  Логарифмирование уравненийЯсно, что если от равных величин взять логарифмы по одному и тому же основанию, то тогда эти логарифмы окажутся также равными. Если подобный прием применяют при решении урав-ния, то, говорят, что производится логарифмирование уравнения. Иногда оно позволяет решить некоторые особо сложные примеры. Задание. Укажите корни урав-ния Здесь переменная величина находится одновременно и в основании степени, и в ее показателе. Возьмем от правой и левой части урав-ния логарифм по основанию 5: Возвращаемся от переменной t к переменной х: Видео:Проще простого! Как решить Логарифмическое Уравнение?Скачать  Переход от логарифмических неравенств к нелогарифмическимРассмотрим график логарифмической функции у = logax при условии а > 1. Она является возрастающей функцией. Если на оси Ох отложить два числа tи s так, чтобы t располагалось левее s (то есть t 1). Но это не совсем так. Дело в том, что надо учесть ещё и тот факт, что под знаком логарифма может стоять исключительно положительное число. Получается, что от простейшего логарифмического неравенства Естественно, вместо величин t и s могут стоять как числа, так и выражения с переменными. Задание. Найдите решение логарифмического неравенства Ответ можно оставить и в такой форме, однако всё же принято записывать его в виде промежутка. Очевидно, что нерав-во 0 logas: Но, снова-таки, мы должны учесть, числа t может быть лишь положительным (тогда s, которое больше t, автоматически также окажется положительным). Получается, что при 0 loga s можно перейти к двойному нерав-ву 0 2 – 45х + 200 имеет решение Однако в системе (5) есть ещё два неравенства, х > 0 и 45 >x. Их решениями являются промежутки (0; + ∞) и (– ∞; 45). Чтобы определить решение всей системы, отметим на одной прямой решения каждого отдельного нерав-ва и найдем область их пересечения: Видно, что решениями нерав-ва будут являться промежутки (0; 5) и (40; 45), на которых справедливы все три нерав-ва, входящих в систему (5). Видео:11 класс, 17 урок, Логарифмические уравненияСкачать  Логарифмические уравнения и системып.1. Методы решения логарифмических уравненийПри решении логарифмических уравнений используются следующие основные методы: п.2. Решение уравнений вида (log_a f(x)=log_a g(x))Неравенства ( begin f(x)gt 0\ g(x)gt 0 end ) в системе соответствуют ограничению ОДЗ для аргумента логарифмической функции. Решать логарифмическое уравнение принято в таком порядке: Однако, если выражения (f(x)) и (g(x)) слишком сложны для явного решения, возможен другой порядок действий: Например: п.3. Решение уравнений вида (log_ f(x)=log_ g(x))Как и в предыдущем случае, можно сначала найти ОДЗ, а потом решать уравнение. Например: В логарифмическом уравнении перед отбрасыванием логарифмов основания обязательно должны быть равны. Не забывайте это проверять! Например: Преобразования могут расширить первоначальную область допустимых значений (например, при возведении в квадрат), и вы включите в решение лишние корни. п.4. ПримерыПример 1. Решите уравнения: б) ( 2log_5(x-1)=log_5(1,5x+1) ) в) ( log_3(3-x)+log_3(4-x)=1+2log_3 2 ) г) ( log_2^2x+log_2 x^2+1=0 ) д) ( x^=10 ) e) ( sqrtcdot log_5(x+3)=0 ) ж) ( log_2+2log_x=log_(x+1) ) Пример 2*. Решите уравнения: б) ( log_2(9-2^x)=25^<log_5sqrt> ) в) ( lgsqrt+lgsqrt+1=lg 30 ) г) ( frac+frac+frac=0 ) e) ( x^<frac>=10^ ) ж) ( 4^=(2x^2+2x+5)^ ) Пример 3. Решите систему уравнений: б) ( begin x^=27\ x^=frac13 end ) в*) ( begin 3(log_y x-log_x y)=8\ xy=16 end ) г*) ( begin (x+y)cdot 3^=frac\ 3log_5(x+y)=x-y end ) 📸 ВидеоРешение логарифмических уравнений. Вебинар | МатематикаСкачать  Логарифмы с нуля за 20 МИНУТ! Introduction to logarithms.Скачать  Решение логарифмических уравнений и неравенствСкачать  Математика. Методы решения логарифмических уравнений (1-2)Скачать  Старт Щелчка. №14 Неравенства с нуля и до ЕГЭ за 5 часов | Логарифмы, степени для №5,6,12Скачать  Шпаргалка для школьника — Все Свойства Логарифмов за 15 минутСкачать  Логарифмические неравенства. 11 класс.Скачать  Как Решать Логарифмические Уравнения Быстрее? СЕКРЕТНЫЙ МЕТОДСкачать  Умножаем логарифмы В УМЕ🧠Скачать  Логарифм с нуля до уровня про. Уравнения, неравенства и параметр. Профильный ЕГЭСкачать  Интересная задача на логарифмы в ЕГЭСкачать  |
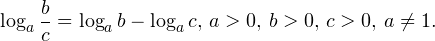 0,, b>0,, c>0,, ane 1. ]» title=»Rendered by QuickLaTeX.com»/>
0,, b>0,, c>0,, ane 1. ]» title=»Rendered by QuickLaTeX.com»/>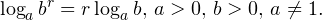 0,, b>0,, ane 1. ]» title=»Rendered by QuickLaTeX.com»/>
0,, b>0,, ane 1. ]» title=»Rendered by QuickLaTeX.com»/>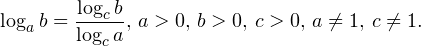 0,, b>0,, c>0,, ane 1,, cne 1. ]» title=»Rendered by QuickLaTeX.com»/>
0,, b>0,, c>0,, ane 1,, cne 1. ]» title=»Rendered by QuickLaTeX.com»/>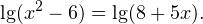
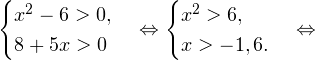 0, \ 8+5x > 0 end Leftrightarrow begin x^2 > 6, \ x>-1,6. end Leftrightarrow ]» title=»Rendered by QuickLaTeX.com»/>
0, \ 8+5x > 0 end Leftrightarrow begin x^2 > 6, \ x>-1,6. end Leftrightarrow ]» title=»Rendered by QuickLaTeX.com»/>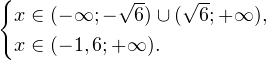
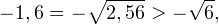 -sqrt, ]» title=»Rendered by QuickLaTeX.com»/>
-sqrt, ]» title=»Rendered by QuickLaTeX.com»/>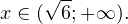
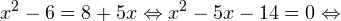
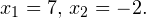
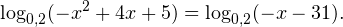
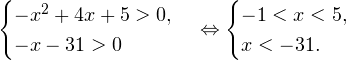 0, \ -x-31>0 endLeftrightarrow begin -1
0, \ -x-31>0 endLeftrightarrow begin -1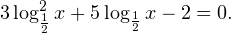
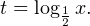
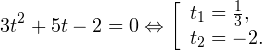
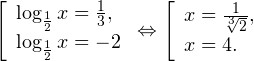
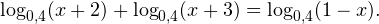
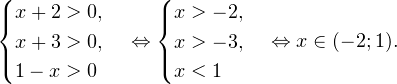 0, \ x+3>0, \ 1-x>0 endLeftrightarrow begin x>-2, \ x>-3, \ x
0, \ x+3>0, \ 1-x>0 endLeftrightarrow begin x>-2, \ x>-3, \ x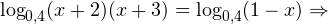
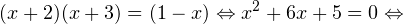
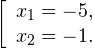
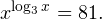
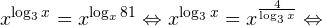
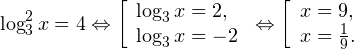
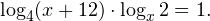
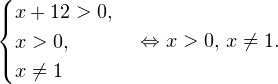 0, \ x>0, \ xne 1 endLeftrightarrow x>0,, xne 1. ]» title=»Rendered by QuickLaTeX.com»/>
0, \ x>0, \ xne 1 endLeftrightarrow x>0,, xne 1. ]» title=»Rendered by QuickLaTeX.com»/>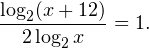
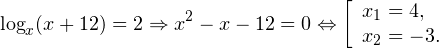
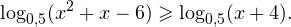
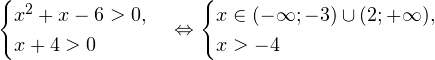 0, \ x+4>0 endLeftrightarrow begin xin(-mathcal;-3)cup(2;+mathcal), \ x>-4 end ]» title=»Rendered by QuickLaTeX.com»/>
0, \ x+4>0 endLeftrightarrow begin xin(-mathcal;-3)cup(2;+mathcal), \ x>-4 end ]» title=»Rendered by QuickLaTeX.com»/>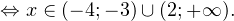
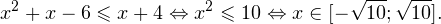
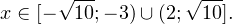
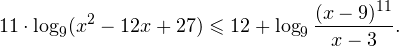
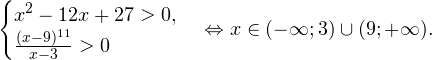 0, \ frac<(x-9)^>>0 endLeftrightarrow xin(-mathcal;3)cup(9;+mathcal). ]» title=»Rendered by QuickLaTeX.com»/>
0, \ frac<(x-9)^>>0 endLeftrightarrow xin(-mathcal;3)cup(9;+mathcal). ]» title=»Rendered by QuickLaTeX.com»/>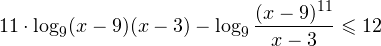
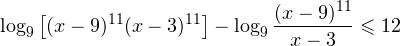
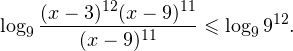
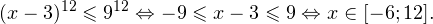
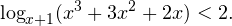
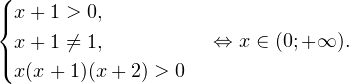 0, \ x+1ne 1,\ x(x+1)(x+2)>0 endLeftrightarrow xin (0;+mathcal). ]» title=»Rendered by QuickLaTeX.com»/>
0, \ x+1ne 1,\ x(x+1)(x+2)>0 endLeftrightarrow xin (0;+mathcal). ]» title=»Rendered by QuickLaTeX.com»/>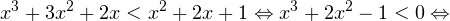
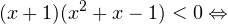
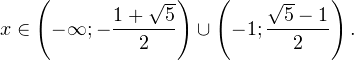
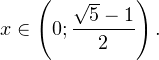
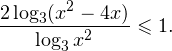
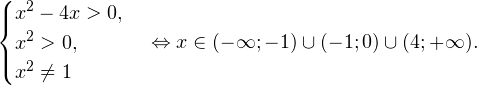 0, \ x^2>0, \ x^2ne 1 endLeftrightarrow xin(-mathcal;-1)cup(-1;0)cup(4;+mathcal). ]» title=»Rendered by QuickLaTeX.com»/>
0, \ x^2>0, \ x^2ne 1 endLeftrightarrow xin(-mathcal;-1)cup(-1;0)cup(4;+mathcal). ]» title=»Rendered by QuickLaTeX.com»/>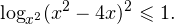
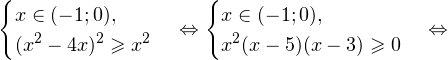
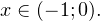
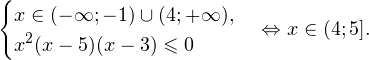
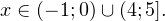
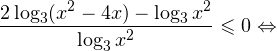
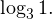 Это ничего не изменит, поскольку
Это ничего не изменит, поскольку 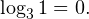
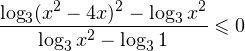
 и
и  — одного знака при
— одного знака при 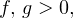 0,» title=»Rendered by QuickLaTeX.com» height=»18″ width=»74″ style=»vertical-align: -4px;»/> в области допустимых значений имеет место следующий равносильный переход:
0,» title=»Rendered by QuickLaTeX.com» height=»18″ width=»74″ style=»vertical-align: -4px;»/> в области допустимых значений имеет место следующий равносильный переход: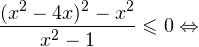
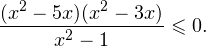
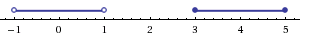
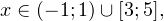 а с учетом области допустимых значений получаем тот же результат:
а с учетом области допустимых значений получаем тот же результат: