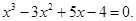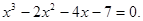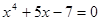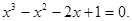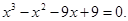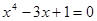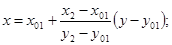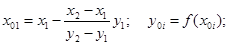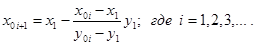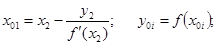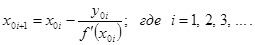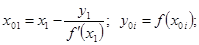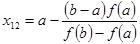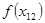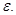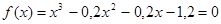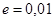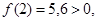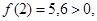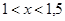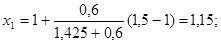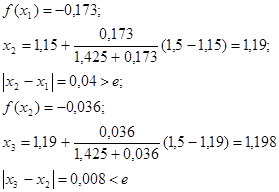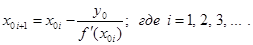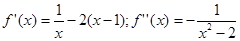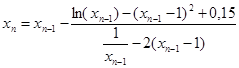Видео:1,2 Решение нелинейных уравнений методом хордСкачать

Численные методы решения нелинейных уравнений. Метод хорд.
Метод хорд ( метод также известен как Метод секущих ) один из методов решения нелинейных уравнений и основан на последовательном сужении интервала, содержащего единственный корень уравнения 

В отличие от метода половинного деления, метод хорд предлагает, что деление рассматриваемого интервала будет выполняться не в его середине, а в точке пересечения хорды с осью абсцисс (ось — Х). Следует отметить, что под хордой понимается отрезок, который проведен через точки рассматриваемой функции по концам рассматриваемого интервала. Рассматриваемый метод обеспечивает более быстрое нахождение корня, чем метод половинного деления, при условии задания одинакового рассматриваемого интервала.
Геометрически метод хорд эквивалентен замене кривой 


Рис.1. Построение отрезка (хорды) к функции 
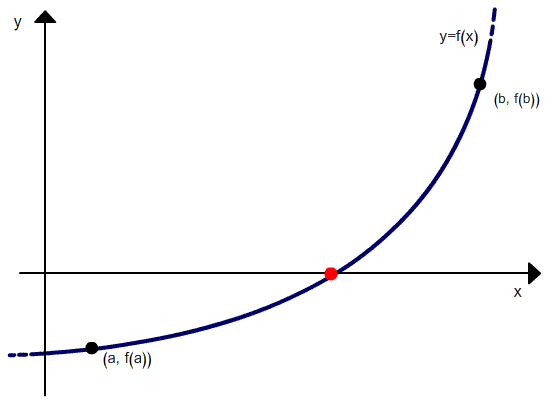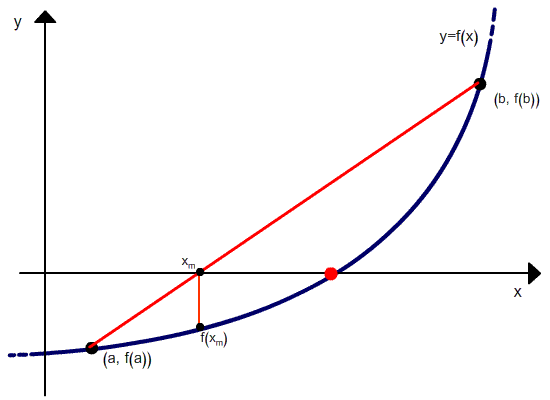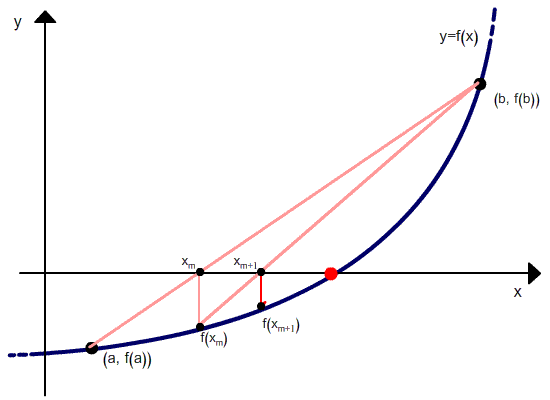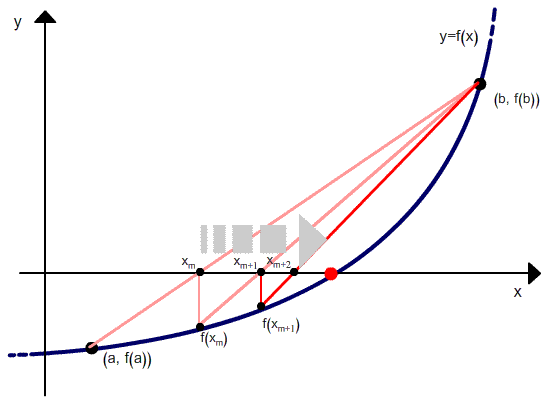
Уравнение прямой (хорды), которая проходит через точки А и В имеет следующий вид:
Данное уравнение является типовым уравнением для описания прямой вы декартовой системе координат. Наклон кривой задается по ординате и абсциссе с помощью значений в знаменателе 

Для точки пресечения прямой с осью абсцисс 
В качестве нового интервала для прохождения итерационного процесса выбираем один из двух 




Итерационный процесс уточнения корня заканчивается, когда условие близости двух последовательных приближений станет меньше заданной точности, т.е.

Рис.2. Пояснение к определению погрешности расчета.
Следует отметить, что сходимость метода хорд линейная, однако более быстрая, чем сходимость метода половинного деления.
Алгоритм нахождения корня нелинейного уравнения по методу хорд
1. Найти начальный интервал неопределенности 


2. Найти точку пересечения хорды с осью абсцисс:
3. Необходимо найти значение функции 



— если выполняется условие 


— если выполняется условие 


В результате находится новый интервал неопределенности, на котором находится искомых корень уравнения:
4. Проверяем приближенное значение корня уравнения на предмет заданной точности, в случае:
— если разность двух последовательных приближений станет меньше заданной точности 
— если разность двух последовательных приближений не достигает необходимой точности 

Видео:Метод хорд для приближённого решения алгебраических уравненийСкачать

Пример решения уравнений методом хорд
В качестве примера, рассмотрим решение нелинейного уравнения 


Вариант решения нелинейного уравнения в программном комплексе MathCAD .
Результаты расчетов, а именно динамика изменения приближенного значения корня, а также погрешности расчета от шага итерации представлены в графической форме (см. рис.1).
Рис.1. Результаты расчета по методу хорд
Для обеспечения заданной точности 


Примечание:
Модификацией данного метода является метод ложного положения ( False Position Method ), который отличается от метода секущих только тем, что всякий раз берутся не последние 2 точки, а те точки, которые находятся вокруг корня.
Следует отметить, что в случае если от нелинейной функции можно взять вторую производную 

Случай №1: 
f»(a)>0″ width=»158″ height=»20″ border=»0″ />
Из первого условия получается, что неподвижной стороной отрезка является – сторона a .
Случай №2: 
Из второго условия получается, что неподвижной стороной отрезка является – сторона b .
В общем виде, для выявления неподвижного конца можно записать следующее условие: 


Рис. 3. Примеры убывающей или возрастающей функции
Таким образом, в зависимости от вида функции получаются два выражения для упрощения поиска корня функции:
— если функция соответствует первому случаю (см. рис. 3), тогда формула будет иметь следующий вид:

— если функция соответствует второму случаю (см. рис. 3), тогда формула будет иметь следующий вид:

Случай 

Для того, чтобы добавить Ваш комментарий к статье, пожалуйста, зарегистрируйтесь на сайте.
Видео:Численное решение уравнений, урок 3/5. Метод хордСкачать

Метод хорд
Метод хорд — итерационный численный метод приближённого нахождения корня уравнения.
Немного теории о методе хорд под калькулятором.
Метод хорд
Метод хорд
Метод хорд можно рассматривать как комбинацию метода секущих (Метод секущих) и метода дихотомии — отличие от метода секущих состоит в том, что если в методе секущих в качестве точек следующей итерации выбираются последние рассчитанные точки, то в методе хорд выбираются те точки, в которых функция имеет разный знак, и соответственно, выбранный интервал содержит корень.
Вывод итерационной формулы аналогичен выводу формулы для метода секущих:
Положим, что у нас есть две точки, x0 и x1, в которых значения функции равны соответственно f(x0) и f(x1). Тогда уравнение прямой, проходящей через эти точки, будет
Для точки пересечения с осью абсцисс (у=0) получим уравнение
Но в отличие от метода секущих, после расчета следующего приближения в качестве второй точки выбирается не последняя, а та, в которой функция имеет разный знак со значением функции в вычисленной точке. Проиллюстрировано это ниже.
Метод хорд является двухшаговым, то есть новое приближение определяется двумя предыдущими итерациями. Поэтому необходимо задавать два начальных приближения корня.
Метод требует, чтобы начальные точки были выбраны по разные стороны от корня (то есть корень содержался в выбранном интервале), при этом величина интервала в процессе итераций не стремится к 0.
В качестве критерия останова берут один из следующих:
— значение функции на данной итерации стало меньше заданого ε.
— изменение хk в результате итерации стало меньше заданого ε. При этом имеется в виду не интервальные значения, а два вычисленных значения, так как величина интервала не стремится к 0.
Видео:Решение нелинейных уравнений методом хордСкачать

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО ЧИСЛЕННЫМ МЕТОДАМ — Тема: Решение алгебраических и трансцендентных уравнений методами хорд и касательных.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО ЧИСЛЕННЫМ МЕТОДАМ В СПО
Разработал преподаватель: Игнатьева Елена Сергеевна
Решение алгебраических и трансцендентных уравнений методами хорд и касательных.
— применить умения отделять корни алгебраических уравнений;
— применить умения решать алгебраические уравнений приближенными методами (метод хорд и касательных);
1. Рабочая тетрадь в клетку.
2. Раздаточный материал: инструкционные карты-20шт.
3. Калькулятор простой.
1. Методом хорд с точностью до 0,01 найдите приближенное значение наибольшего действительного корня следующего алгебраического уравнения.
2. Методом касательных с точностью до 0,01 найдите приближенное значение наибольшего действительного корня следующего алгебраического уравнения.
3. Комбинированным методом хорд и касательных решить уравнение с точностью до 0,01.
1. Методом хорд с точностью до 0,01 найдите приближенное значение наибольшего действительного корня следующего алгебраического уравнения.
2. Методом касательных с точностью до 0,01 найдите приближенное значение наибольшего действительного корня следующего алгебраического уравнения.
3. Комбинированным методом хорд и касательных решить уравнение с точностью до 0,01.
1. Внимательно прочитать тему и цель практической работы .
2. Изучить учебный материал по теме.
3. Ответить на вопросы.
4. Выполнить задания.
5. Подготовить отчет.
Пояснения к работе (учебный материал):
Предположим, что удалось найти достаточно малый промежуток 
Тогда, согласно теореме 5, непрерывная и дифференцируемая функция 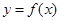
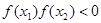
Предположим, также, что промежуток 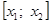
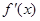
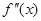
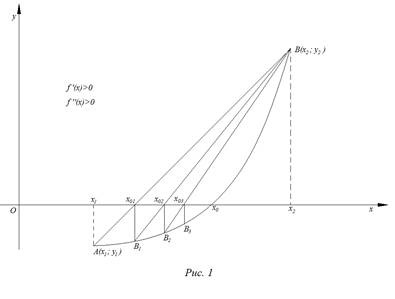
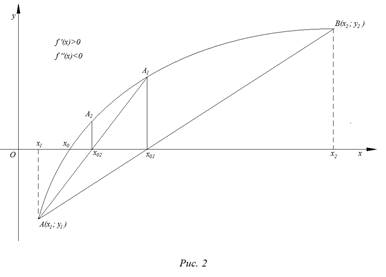
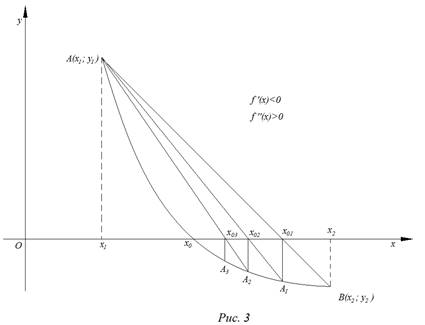
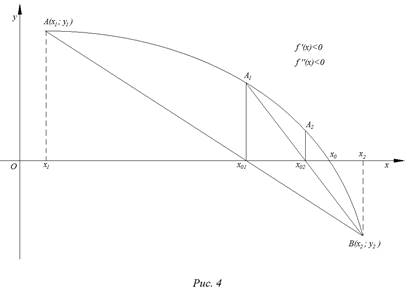
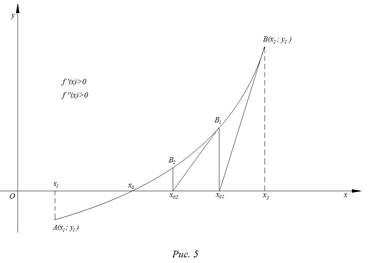
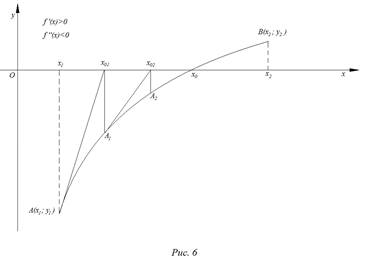
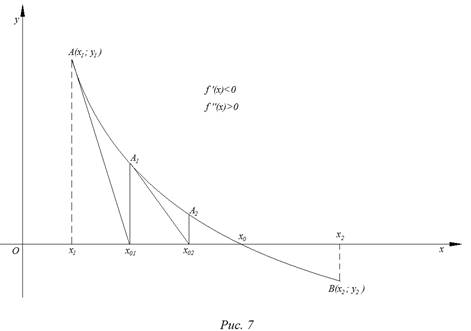
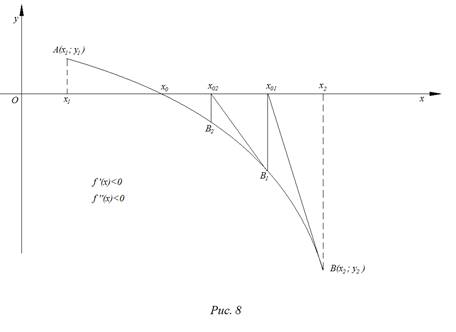
На рис. 1 – 4 изобразим схематические графики четырёх типов расположения дуги кривой.
Отдельно рассмотрим и опишем два случая.
Случай 1. 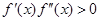
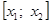
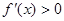
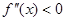
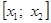
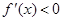
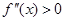
Случай 2. 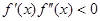
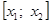
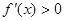
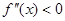
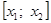
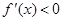
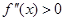
Приведем алгоритм решения задачи в первом случае:
а) через точки 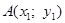
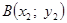
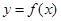
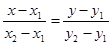
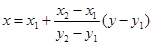
б) найдём абсциссу точки пересечения хорды АВ с осью Ох. Положив 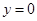
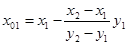
в) подставив значение 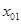
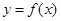
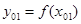
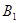
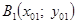
г) через точки 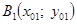
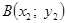
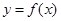
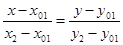
д) найдем абсциссу точки пересечения хорды 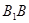
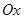
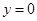
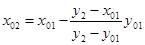
е) в результате получим последовательность значений 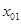
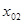
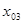
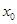
После выполнения неравенства 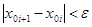
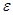
Итак, в первом случае вычисления производятся по формулам:
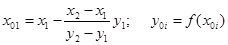
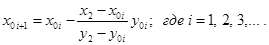
Приведем алгоритм решения задачи во втором случае:
а) значения 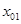
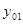
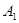
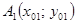
б) через точки 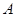
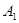
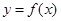
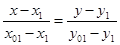
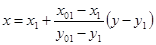
в) найдем абсциссу точки пересечения хорды 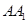
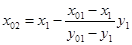
г) дальнейшие действия такие же, как и в первом случае. Итак, во втором случае вычисления производятся по формулам:
Метод касательных (метод Ньютона).
При тех же предложениях, что и в методе хорд на рис. 5 и 8, изобразим схематически графики четырех типов расположения дуги кривой.
Отдельно рассмотрим и опишем два случая.
Случай 1. . 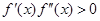
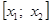
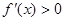
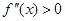
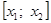
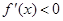
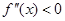
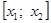
Случай 2. 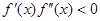
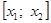
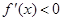
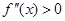
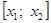
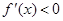
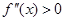
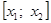
Приведем алгоритм решения задачи в первом случае:
а) через точку 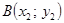
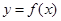
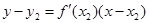
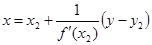
б) найдём абсциссу точки пересечения этой касательной с осью Ox . Положив 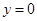
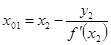
в) подставив значение 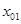
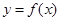
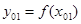
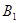
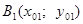
г) через точку 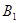
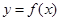
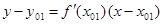
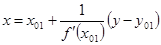
д) найдём абсциссу точки пересечения этой касательной с осью Ox . Положив 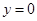
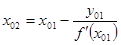
е) в результате получим последовательность значений 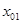
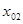
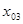
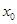
После выполнения неравенства 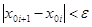
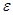
Итак, в первом случае вычисления производятся по формулам:
Алгоритм решения задачи во втором случае будет таким же, как и в первом случае, только первая касательная будет проводиться через точку 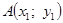
Итак, во втором случае вычисления проводятся по формулам:
Комбинированный метод хорд и касательных.
Пусть требуется найти действительный корень уравнения 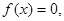
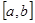
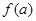
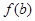
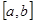
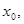
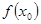
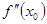
Воспользуемся формулами методов хорд и касательных:
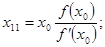
Величины 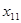
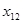
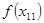
Построим новую пару приближений к корню:
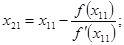
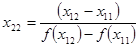
Точки 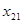
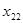
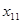
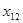
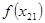
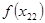
Вычислим теперь значения
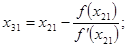
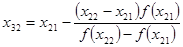
Каждая из последовательностей
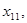
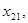
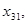
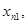
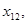
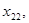
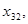
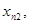
стремится к искомому корню, причем одна из последовательностей монотонно возрастает, а другая – монотонно убывает. Пусть, например, 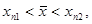
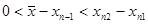
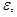
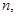
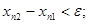
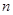
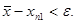
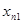
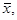
Так, например, для нахождения приближенного значения 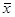
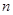
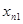
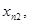
При выполнении практической работы рассмотрите следующие примеры:
Методом хорд найти положительный корень уравнения
С точностью
Прежде всего, отделяем корень. Так как
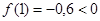
То искомый корень х лежит в интервале 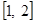
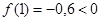
То искомый корень х лежит в интервале 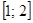
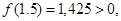
Так как 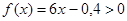
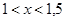
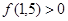
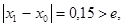
Таким образом, можно принять 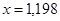
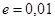
Заметим, что точный корень уравнения 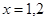
С помощью графического метода отделить корни трансцендентного уравнения и уточнить их методом Ньютона с точностью е=0,00001.
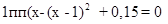
Решение. Запишем наше уравнение в виде 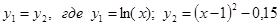
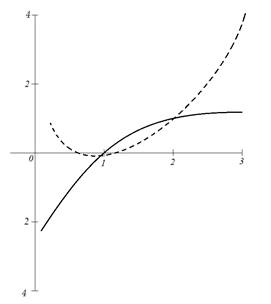
Из рис. 3 видно, что данное уравнение имеет два корня: первый корень принадлежит отрезку [0,1; 1], а второй [1,1; 2].
Итерационная формула метода Ньютона в данном случае принимает вид.
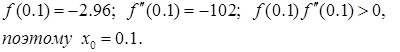
💡 Видео
Решение нелинейного уравнения методом хорд (секущих) (программа)Скачать

Метод Ньютона (метод касательных) Пример РешенияСкачать

Метод хордСкачать

Алгоритмы. Нахождение корней уравнения методом хордСкачать

Метод секущихСкачать

Методы решения систем нелинейных уравнений. Метод Ньютона. Численные методы. Лекция 14Скачать

МЗЭ 2021 Лекция 11 Метод Ньютона для решения систем нелинейных уравненийСкачать

10 Численные методы решения нелинейных уравненийСкачать

Метод Хорд - ВизуализацияСкачать

Методы численного анализа - Метод Ньютона, секущих для решения систем нелинейных уравненийСкачать

Численное решение уравнений, урок 5/5. Комбинированный метод хорд и касательныхСкачать

4.2 Решение систем нелинейных уравнений. МетодыСкачать

15 Метод Ньютона (Метод касательных) Ручной счет Численные методы решения нелинейного уравненияСкачать

Метод касательных для приближённого решения алгебраических уравненийСкачать

Алгоритмы С#. Метод Ньютона для решения систем уравненийСкачать

метод хордСкачать