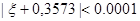Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
БИК Курс лекций по дисциплине «Численные методы»
для специальности 230105 Программное обеспечение вычислительной техники и автоматизированных систем
Раздел 2. Численные методы
2.1.1. Приближенные решения алгебраических и трансцендентных уравнений
Алгебраические и трансцендентные уравнения
Графический метод решения уравнений
1. Алгебраические и трансцендентные уравнения
При решении практических задач часто приходится сталкиваться с решением уравнений. Всякое уравнение с одним неизвестным можно представить в виде

где 
В общем случае нелинейное уравнение можно записать в виде:
F ( x ) определена и непрерывна на конечном или бесконечном интервале 
Совокупность значений переменной х, при которых уравнение (1) превращается в тождество, называется решением этого уравнения, а каждое значение х : из этой совокупности называется корнем уравнения.
Всякое число 

Число 

F ( 


Однократный корень называется простым.
Решить уравнение – значит найти множество всех корней этого уравнения.
Оно может быть конечным или бесконечным.
Два уравнения F ( x )=0 и G ( x =0) называются равносильными (эквивалентными), если всякое решение каждого из них является решением и для другого, то есть множества решений этих уравнений совпадают.
В зависимости от того, какие функции входят в уравнения (1) или (2), уравнения разделяются на два больших класса: линейные и нелинейные.
Нелинейные уравнения делятся, в свою очередь на: алгебраические и трансцендентные .
Уравнение (2) называется алгебраическим, если функция является алгебраической функцией. Путем алгебраических преобразований из всякого алгебраического уравнения можно получить уравнение в канонической форме:
где a 0, a 1, . , a n — коэффициенты уравнения, а x -неизвестное. Показатель n называется степенью алгебраического уравнения.
Если функция F ( x ) не является алгебраической, то уравнение (1) называется трансцендентным.
В некоторых случаях решение трансцендентных уравнений можно свести к решению алгебраических уравнений.
Решение уравнения с одним неизвестным заключается в отыскании корней, т. е. тех значений х, которые обращают уравнение в тождество. Корни уравнения могут быть вещественными и невещественными (комплексными).
Найти точные значения корней уравнения можно только в исключительных случаях, обычно, когда есть какая-либо простая формула для вычисления значения корней, выражающая их через известные величины.
Поскольку подавляющее большинство нелинейных уравнений с одной переменой не решаются путем аналитических преобразований (точными методами), на практике их решают только численными методами.
При решении многих практических задач точное решение уравнения не всегда является необходимым. Задача нахождения корней считается решенной, если корни вычислены с заданной степенью точности.
Решить уравнение – это значит
установить, имеет ли оно корни,
и найти значение корней с заданной точностью.
Задача численного нахождения действительных и комплексных корней уравнения (2) обычно состоит из двух этапов:
отделение корней, т.е. нахождение достаточно малых окрестностей рассматриваемой области, в которых находится одно значение корня,
и уточнение корней, т.е. вычисление корней с заданной степенью точности в некоторой окрестности.
Наиболее распространенными на практике численными методами решения уравнения (2) являются: метод половинного деления, метод хорд, метод касательных (Ньютона), комбинированный метод, метод простой итерации. Применение того или иного метода для решения уравнения (2) зависит от числа корней, задания исходного приближения и поведения функции F ( x ).
2. Графические методы решения уравнений
Одним из методов решения уравнений является графический. Точность такого решения невелика, однако с помощью графика можно разумно выбрать первое приближение, с которого начнется дальнейшее решение уравнения. Существуют два способа графического решения уравнений.
Первый способ. Все члены уравнения переносят в левую часть, т. е. представляют его в виде f (х) = 0. После этого строят график функции у = f ( x ), где f (х) – левая часть уравнения. Абсциссы точек пересечения графика функции у = f (х) с осью Ох и являются корнями уравнения, так как в этих точках у = 0 (рис. 1).

Второй способ. Все члены уравнения разбивают на две группы, одну из них записывают в левой части уравнения, а другую в правой, т. е. представляют его в виде f (х) = g (х).
После этого строят графики двух функций у = f (х) и у = g (х). Абсциссы точек пересечения графиков этих двух функций и служат корнями данного уравнения. Пусть точка пересечения графиков имеет абсциссу х0, ординаты обоих графиков в этой точке равны между собой, т. е. f (х0) = g (х0). Из этого равенства следует, что х0 – корень уравнения (рис. 2).

Пример 1. Решить графически уравнение х 3 — 2 x 2 + 2х — 1 = 0.
Первый способ. Построим график функции у = х 3 — 2 x 2 + 2х — 1 и определим абсциссы точек пересечения этого графика с осью Ох. Кривая пересекает ось Ох в точке х = 1, следовательно, уравнение имеет один корень (рис. 3). (Отметим, что алгебраическое уравнение третьей степени имеет или один действительный корень или три. Так как кривая пересекает ось абсцисс только в одной точке, то данное уравнение имеет только один действительный корень. Остальные два корня – комплексные.)


Второй способ. Представим данное уравнение в виде х 3 = 2 x 2 + 2х–1 и построим графики функций у = х 3 и у = 2 x 2 + 2х – 1. Найдем абсциссу точки пересечения этих графиков; получим х = 1 (рис. 4).
Пример 2. Найти приближенно графическим способом корни уравнения lg х — Зх + 5 = 0.
Перепишем уравнение следующим образом: lg х = Зх — 5.
Функции в левой и в правой части уравнения имеют общую область определения: интервал 0
Строим графики функций у = lg х и у = Зх — 5 (рис. 5). Прямая у = Зх-5 пересекает логарифмическую кривую в двух точках с абсциссами x 1 





Пример 3. Найти графически корни уравнения 2 х = 2х.
Решение. Строим графики функций у = 2 х и у = 2х. Эти графики пересекаются в двух точках, абсциссы которых равны х 1 = 1 и х 2 = 2. Данное уравнение имеет два корня х 1 = 1 и х 2 = 2 (рис. 6).
Подводя итог вышеизложенному, можно рекомендовать для графического решения уравнения f (х) = 0, все корни которого лежат в промежутке [а, b ], следующую простую схему.
1. Представить указанное уравнение в виде 

2. На бумаге вычертить графики функций у =
3. Если графики не пересекаются, то корней в данном промежутке нет. Если же графики пересекаются, то нужно определить точки их пересечения, найти абсциссы этих точек, которые и будут приближенными значениями корней рассматриваемого уравнения.
Первый этап численного решения уравнения (2) состоит в отделении корней, т.е. в установлении “тесных” промежутков, содержащих только один корень.
Корень 
Отделить корни – это значит разбить всю область допустимых значений на отрезки, в каждом из которых содержится один корень.
Отделение корней можно произвести двумя способами – графическим и аналитическим.
Графический метод отделения корней. При графическом методе отделения корней поступают так же, как и при графическом методе решения уравнений.
Графический метод отделения корней не обладает большой точностью. Он дает возможность грубо определить интервалы изоляции к орня. Далее корни уточняются одним из способов, указанных ниже.
Аналитический метод отделения корней. Аналитически корни уравнения f(х) =0 можно отделить, используя некоторые свойства функций, изучаемые в курсе математического анализа.
Сформулируем без доказательства теоремы, знание которых необходимо при отделении корней.
1) Если непрерывная на отрезке 
2) Если функция F ( x ) к тому же еще и строго монотонна, то корень на отрезке 
Рассмотрим примеры поведения некоторых функций:


Для отделения корней можно эффективно использовать ЭВМ.
П

Как только обнаружится пара соседних значений F ( x ), имеющих разные знаки, и функция F ( x ) монотонна на этом отрезке, так соответствующие значения аргумента X (предыдущее и последующее) можно считать концами отрезка, содержащего корень.
Схема соответствующего алгоритма изображена ниже. Результатом решения поставленной задачи будут выводимые на дисплей в цикле значения параметров X 1 и X 2 (Концов выделенных отрезков).
- Реферат: Приближенное решение алгебраических и трансцендентных уравнений Метод Ньютона
- История метода
- Отделение корней
- Описание метода Ньютона (метода касательных)
- Оценка погрешности
- Погрешность
- Условие сходимости
- Метод половинного деления
- Погрешность
- Пример решения уравнения методом Ньютона
- Список литературы
- Решение алгебраических и трансцендентных уравнений
- 🎬 Видео
Видео:10 Численные методы решения нелинейных уравненийСкачать

Реферат: Приближенное решение алгебраических и трансцендентных уравнений Метод Ньютона
| Название: Приближенное решение алгебраических и трансцендентных уравнений Метод Ньютона Раздел: Рефераты по математике Тип: реферат Добавлен 04:59:04 04 января 2011 Похожие работы Просмотров: 261 Комментариев: 14 Оценило: 3 человек Средний балл: 5 Оценка: неизвестно Скачать | ||||||||||||||||||||||||||||||||||||||
| n | xn | f(xn) | f'(xn) | hn |
| 0 | 0 | 1 | 3 | -0,333333333 |
| 1 | -0,3 33333333 | 0,062142078 | 2,606445364 | -0,023841696 |
| 2 | -0,357 175029 | 0,000392296 | 2,573426701 | -0,000152441 |
| 3 | -0,35732747 0 | 1,63265E-08 | 2,573213436 | -6,34481E-09 |
| 4 | -0,357327477 | 2,9976E-15 | 2,573213427 | -1,16493E-15 |
| 5 | -0,357327477 | 0 | 2,573213427 | 0 |
Вывод: в третьем приближении получен результат с 4-мя точными знаками после запятой: 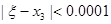
Ответ:
Видео:Метод половинного деления. ДихотомияСкачать

Список литературы
· «Основы вычислительной математики», Б. П. Демидович, И.А. Марон, 1966г.
Видео:Метод хорд для приближённого решения алгебраических уравненийСкачать

Решение алгебраических и трансцендентных уравнений
Составитель: Панкратов Ю.M.
Лабораторная работа №3
Целью работы является знание приемов отделения корней и численных методов приближенного решения алгебраических и трансцендентных уравнений.
1. Теоретические сведения
1.1. Отделение корней
Отыскание приближенных значений корней уравнений состоит из двух этапов – отделение корней и их уточнение с заданной степенью точности. Отделение корней представляет процедуру по разбиению всей области числовой оси на интервалы, в каждом из которых содержится один корень, и ее можно выполнить двумя способами – графическим и аналитическим. При графическом методе строят график функции, который позволяет легко находить отрезки, заключающие в себе только один корень. При аналитическом методе корни уравнения f(x)=0 можно отделить, используя следующую теорему:
Если функция f(x) непрерывна на отрезке [a,b] и принимает на концах отрезка значения разных знаков, а производная f’(x) сохраняет постоянный знак внутри отрезка, то внутри отрезка существует корень уравнения f(x)=0 и при том единственный.
Поскольку MathCAD позволяет достаточно просто построить график любой функции, то воспользуемся графическим методом, учитывая утверждения этой теоремы. Тогда отделение корней можно выполнить в следующем порядке:
1. Построить график функции f(x) в интервале, охватывающем все корни уравнения. Если этот интервал очень большой, то можно построить несколько графиков для каждого корня в увеличенном масштабе.
2. Под этим графиком в том же масштабе по оси абсцисс построить график первой производной f’(x).
3. Проанализировав эти графики с учетом вышеизложенной теоремы, уже можно, хотя и довольно грубо, указать границы интервалов [ai ,bi] для каждого i-го корня.
4. Более наглядно и точнее эту задачу можно решить, если построить еще один совмещенный график сигналов функции f(x) и ее первой производной f’(x). Например, сигнал значений функции f(x) принять равным 1.5, сигнал значений первой производной f’(x) принять равным 1 (чтобы не сливались при совпадении). Функции этих сигналов можно вычислить как
sf(x):=1.5 sign(f(x) — для функции f(x);
sf1(x):= sign(f1(x) — для первой производной f’(x), где f1(x) — первая производная f’(x).
При выборе границ интервалов [ai ,bi] для каждого корня надо учитывать, что они не должны совпадать или даже близко приближаться к точкам экстремумов функции f(x) или, что то же самое, к значениям x , при которых f’(x)=0. В этих областях для некоторых методов уточнения корней сходимость итерационных процессов в выбранном интервале [ai ,bi] не гарантирована.
1.2. Уточнение корней
В работе рассматриваются только четыре метода уточнения корней. Считаем, что абсциссы xa и xb границ интервала [ai ,bi] , содержащего единственный корень, известны.

1. Вычисляют абсциссу xc средней точки, делящей отрезок [ai ,bi] пополам (Рис.1.) xc = (xa+xb)/2 ;
2. Вычисляют значение функции f(xc) в средней точке;
3. 
4. Если |xb — xa| > e , то цикл повторяют, начиная с п.1, в противном случае считают, что найденное значение и есть корень уравнения этого интервала, вычисленный с точностью e.
Достоинства метода: простота алгоритма, высокая надежность отыскания корня. Недостаток – большое количество шагов итераций.
1. Одну из граничных точек принимают за неподвижную точку xc . Обычно это точка, в которой знак функции совпадает со знаком второй производной, т.е. f(xc)× f’’(xc) > 0. Тогда вторую граничную точку принимают за начальное приближение x0 (Рис.2.) ;
2. Каждое следующее значение абсциссы xi+1 вычисляют как точку пересечения хорды, соединяющей неподвижную точку xc и крайнюю текущую точку кривой xi , с осью абсцисс по формуле:
3. Если |xi+1 – xi | > e , то цикл повторяют, начиная с п.2, в противном случае считают, что найденное значение и есть корень уравнения этого интервала, вычисленный с точностью e.
Метод обладает теми же достоинствами и недостатками, как и предыдущий.

1. За начальное приближение x0 принимают граничную точку, в которой знак функции совпадает со знаком второй производной, т.е. f(x0)×f’’(x0)> 0 (Рис.3.) ;
2. Каждое следующее значение абсциссы xi+1 вычисляют как точку пересечения касательной, проведенной в текущей точкой кривой xi , с осью абсцисс по формуле:
3. Если |xi+1 – xi | > e , то цикл повторяют, начиная с п.2, в противном случае считают, что найденное значение и есть корень уравнения этого интервала, вычисленный с точностью e.
Достоинства метода: простота алгоритма, высокая скорость сходимости. Недостатки: необходимость отыскания первой производной в аналитической форме, ненадежность отыскания корня в указанном диапазоне. На рис.3 показано, что в случае проведения касательной в точке b , она может пересечься с осью x в точке c, лежащей за пределами выбранного интервала [a,b], и корень может быть найден совсем в другом интервале.
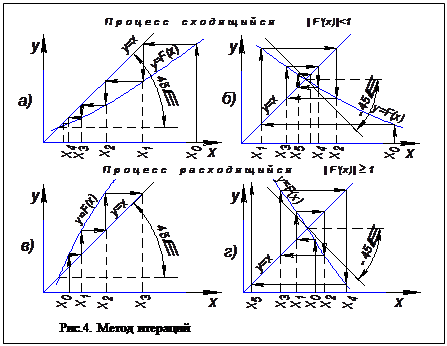
1. Исходное уравнение f(x)=0 преобразуют к виду: x=F(x) (1)
2. Левая часть этого уравнения представляет уравнение прямой линии, проходящей через начало координат под углом в 45° к оси x. Абсцисса пересечения этой прямой с функцией F(x)и представляет корень уравнения f(x)=0(Рис.4.).
3. Задают начальное приближение x0 и вычисляют значение функции F(x0) (см.рис.4а). Из (1) следует, что его можно принять за первое приближение x1 : x1=F(x0).
4. Вычислив функцию F(x1) , принимают это значение за второе приближение x2=F(x1) и так далее. В общем случае для (i+1)-й итерации можно записать:
5. Итерации повторяют, пока выполняется условие |xi+1 – xi | > e .
Геометрическая интерпретация метода показана на рис.4, причем на рис.4а) и 4б) процесс сходится к корню уравнения f(x)=0, а на рис.4в) и 4г) – расходится, хотя начальное приближение x0 и выбрано для них ближе к корню. Из рис.4а) можно заметить, что угол наклона касательной к любой точке кривой y=F(x) не превышает 45° к оси x , т.е. F’(x) -1. На рис.4в) и 4г) это условие не соблюдается и итерационный процесс на них расходится от корня уравнения. Отсюда следует, что для обеспечения сходимости итерационного процесса должно соблюдаться условие:
Оба этих решения можно записать как: -2 0 
Отчет по работе должен включать:
2.1. Отделение корней, для чего необходимо построить графики функции f(x) , ее первой производной f’(x) и график сигналов.
2.2. Уточнение корней методами половинного деления, хорд, касательных и итераций.
2.3. Проверку результатов с помощью встроенной функции root.
3. Пример выполнения задания
1. Бахвалов Н.С. Численные методы. – М., Наука,1975. –632 c.
2. Крылов В.И., Бобков В.В., Монастырный П.И. Вычислительные методы. – М., Наука,1976. –304 с.
3. Волков Е.А. Численные методы : Учебное пособие для вузов. – 2-е изд. – М., Наука, 1987.
4. Копченова Н.В., Марон И.А. Вычислительная математика в примерах и задачах. – М., Наука,1972.
5. Турчак Л.И., Плотников П.В. Основы численных методов: Учеб. пособие.– 2-ое изд., перераб. и доп. -М.: ФИЗМАТЛИТ, 2002. –304 c.
6. Исаков В.Н. Элементы численных методов. – М., Издательский центр «Академия»,2003. –192 c.
🎬 Видео
Решение нелинейного уравнения методом простых итераций (программа)Скачать

Метод половинного деления решение нелинейного уравненияСкачать

Алгебра 10 класс (Урок №1 - Многочлен P(x) и его корень. Алгебраическое уравнение.)Скачать

Метод простых итераций пример решения нелинейных уравненийСкачать

Метод итерацийСкачать

Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Метод секущихСкачать

Трансцендентные уравнения ЕГЭ #maths #calculus #егэ #algebra #огэСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Как найти корни уравнения в Excel с помощью Подбора параметраСкачать

Решение уравнений с помощью ExcelСкачать





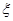 уравнения f ( x ) = 0 отделён на отрезке, причем f ’( x ) и f ’’( x ) непрерывны и сохраняют определённые знаки при
уравнения f ( x ) = 0 отделён на отрезке, причем f ’( x ) и f ’’( x ) непрерывны и сохраняют определённые знаки при 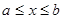 . Найдя какое-нибудь n-e приближение корня
. Найдя какое-нибудь n-e приближение корня 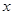 n
n 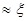 (
(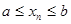 ), мы можем уточнить его по Методу Ньютона следующим образом. Пусть
), мы можем уточнить его по Методу Ньютона следующим образом. Пусть 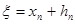 , где hn малая величина. Отсюда, применяя формулу Тейлора, получим:
, где hn малая величина. Отсюда, применяя формулу Тейлора, получим: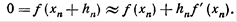
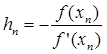
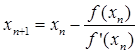 (n=0,1,2…).
(n=0,1,2…).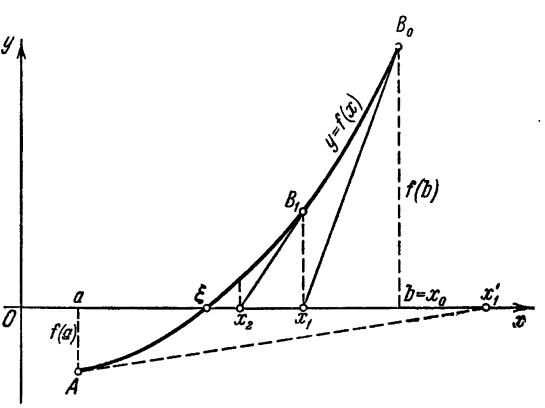
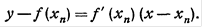
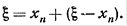
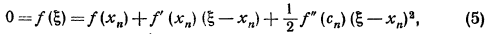
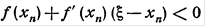
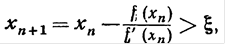
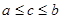 .
.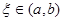 .
.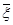 функции f ( x ) такому, что
функции f ( x ) такому, что 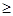 а. Так как в силу положительности производной f ‘ (х) при х > а функция f ( x ) имеет единственный корень на интервале (а, +
а. Так как в силу положительности производной f ‘ (х) при х > а функция f ( x ) имеет единственный корень на интервале (а, +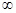 ), то
), то 
 (6)
(6)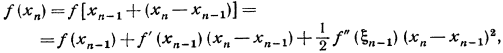 (7)
(7)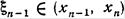 .Так как в силу определения приближения хп имеем
.Так как в силу определения приближения хп имеем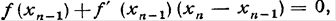

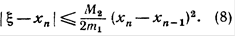
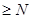 имеем:
имеем: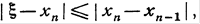
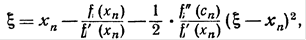
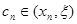 . Отсюда, учитывая формулу (3), будем иметь:
. Отсюда, учитывая формулу (3), будем иметь: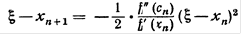
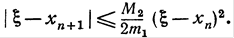 (9)
(9)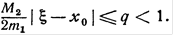
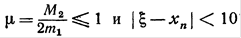
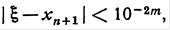
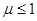 , то с помощью метода Ньютона число верных знаков после запятой искомого корня
, то с помощью метода Ньютона число верных знаков после запятой искомого корня 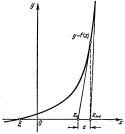
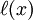 , значения которой совпадают со значениями f (x ) в двух фиксированных точках, в данном случае — в точках xi − 1 и xi .)
, значения которой совпадают со значениями f (x ) в двух фиксированных точках, в данном случае — в точках xi − 1 и xi .)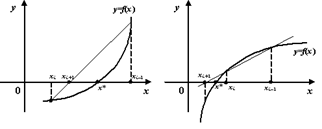
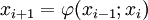 . Найдём выражение для функции
. Найдём выражение для функции 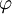 .
.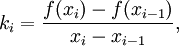
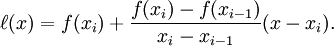
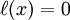 , находим
, находим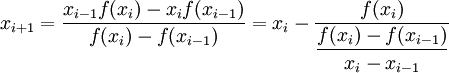
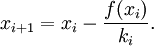 (1)
(1)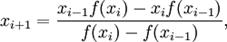
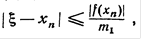
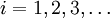 , начиная с двух приближений x 0 и x 1, взятых, по возможности, поближе к корню x * . При этом не предполагается, что x * лежит между x 0 и x 1 (и что значения функции f в точках x 0 и x 1 имеют разные знаки). При этом не гарантируется, что корень попадёт на отрезок между xi − 1 и xi на каком-либо следующем шаге (хотя это и исключено). В таком случае затруднительно дать оценку погрешности, с которой xi + 1 приближает истинное значение корня x * , и поэтому довольствуются таким эмпирическим правилом: вычисления прекращают, когда будет выполнено неравенство
, начиная с двух приближений x 0 и x 1, взятых, по возможности, поближе к корню x * . При этом не предполагается, что x * лежит между x 0 и x 1 (и что значения функции f в точках x 0 и x 1 имеют разные знаки). При этом не гарантируется, что корень попадёт на отрезок между xi − 1 и xi на каком-либо следующем шаге (хотя это и исключено). В таком случае затруднительно дать оценку погрешности, с которой xi + 1 приближает истинное значение корня x * , и поэтому довольствуются таким эмпирическим правилом: вычисления прекращают, когда будет выполнено неравенство 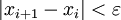 , где
, где 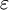 — желаемая точность нахождения корня. При этом полагают приближённое значение корня равным
— желаемая точность нахождения корня. При этом полагают приближённое значение корня равным 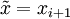 .
.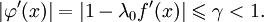 Это неравенство может быть переписано в виде
Это неравенство может быть переписано в виде 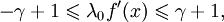 откуда получаем, что сходимость гарантируется, когда, во-первых,
откуда получаем, что сходимость гарантируется, когда, во-первых, 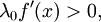 так как
так как 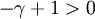 (тем самым проясняется смысл выбора знака числа
(тем самым проясняется смысл выбора знака числа 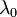 ), а во-вторых, когда
), а во-вторых, когда 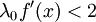 при всех X на всём рассматриваемом отрезке, окружающем корень. Это второе неравенство заведомо выполнено, если
при всех X на всём рассматриваемом отрезке, окружающем корень. Это второе неравенство заведомо выполнено, если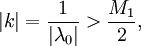
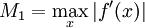 . Таким образом, угловой коэффициент K не должен быть слишком мал по абсолютной величине: при малом угловом коэффициенте уже на первом шаге точка X[1] может выскочить из рассматриваемой окрестности корня X[*] , и сходимость итераций к корню может быть нарушена.
. Таким образом, угловой коэффициент K не должен быть слишком мал по абсолютной величине: при малом угловом коэффициенте уже на первом шаге точка X[1] может выскочить из рассматриваемой окрестности корня X[*] , и сходимость итераций к корню может быть нарушена.
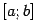 и знаки
и знаки  и
и 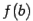 различны (функция
различны (функция 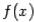 меняет знак при переходе через корень
меняет знак при переходе через корень 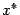 ).
).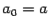 и
и  и вычислим значения функции в левом конце отрезка,
и вычислим значения функции в левом конце отрезка, 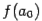 , и в его середине
, и в его середине 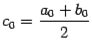 ;
; 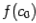 . Сравним знаки чисел
. Сравним знаки чисел 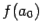 и
и 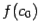 . Если эти знаки различны, то корень
. Если эти знаки различны, то корень 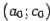 ; если же одинаковы, то тогда различны знаки
; если же одинаковы, то тогда различны знаки 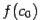 и
и 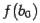 , и корень лежит в интервале
, и корень лежит в интервале 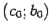 . (Возможен ещё случай
. (Возможен ещё случай 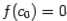 ; тогда корень
; тогда корень 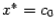 уже найден.) В обоих случаях смены знака корень оказывается отделён на отрезке
уже найден.) В обоих случаях смены знака корень оказывается отделён на отрезке 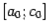 либо
либо 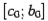 , длина которого ровно в два раза меньше длины исходного отрезка
, длина которого ровно в два раза меньше длины исходного отрезка 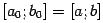 . Обозначим этот отрезок половинной длины через
. Обозначим этот отрезок половинной длины через 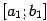 (то есть положим
(то есть положим 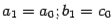 в случае, когда
в случае, когда 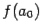 и
и 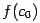 разных знаков, и
разных знаков, и 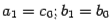 в случае, когда
в случае, когда 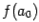 и
и  : снова отыщем его середину
: снова отыщем его середину 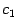 , найдём значение функции
, найдём значение функции 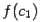 и сравним знак этого числа со знаком
и сравним знак этого числа со знаком 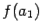 ; если знаки разные, то корень отделён на
; если знаки разные, то корень отделён на 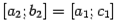 , если одинаковые, то на
, если одинаковые, то на 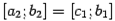 (или же оказывается, что
(или же оказывается, что 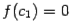 ; тогда корень найден). Длина отрезка, на котором отделён корень, уменьшилась ещё в два раза.
; тогда корень найден). Длина отрезка, на котором отделён корень, уменьшилась ещё в два раза.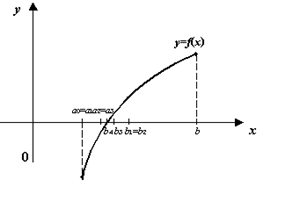
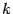 делений длина отрезка, на котором лежит корень, сокращается в
делений длина отрезка, на котором лежит корень, сокращается в 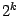 раз и становится равной
раз и становится равной 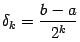 (если корень не был точно определён на каком-то предыдущем этапе, то есть не совпал с
(если корень не был точно определён на каком-то предыдущем этапе, то есть не совпал с 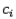 при некотором
при некотором 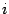 ).
).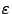 — заданная точность, с которой требуется отыскать корень. Процесс деления отрезков следует остановить, как только станет верным неравенство
— заданная точность, с которой требуется отыскать корень. Процесс деления отрезков следует остановить, как только станет верным неравенство 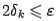 . Очевидно, что если при этом положить
. Очевидно, что если при этом положить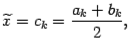
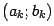 , до середины этого интервала
, до середины этого интервала 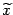 будет не больше
будет не больше 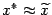 будет выполнено с нужной точностью. C увеличением точности заметно возрастает объем вычислительной работы, поэтому метод удобно применять для нахождения грубого корня уравнения.
будет выполнено с нужной точностью. C увеличением точности заметно возрастает объем вычислительной работы, поэтому метод удобно применять для нахождения грубого корня уравнения.
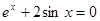 ,
, 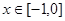 .
.
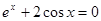
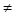 0 при
0 при