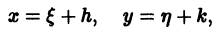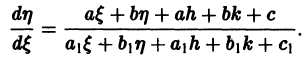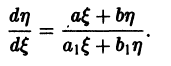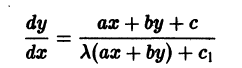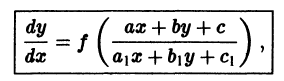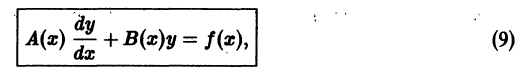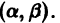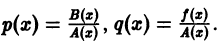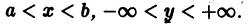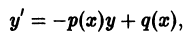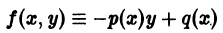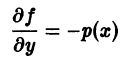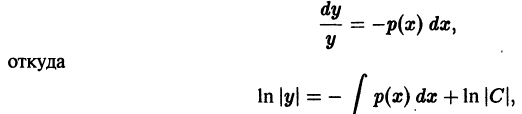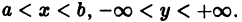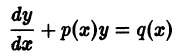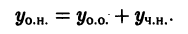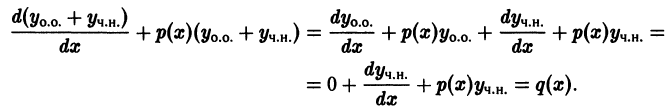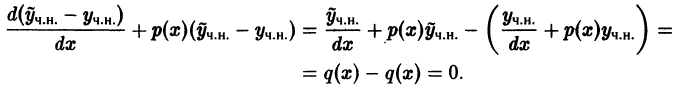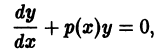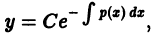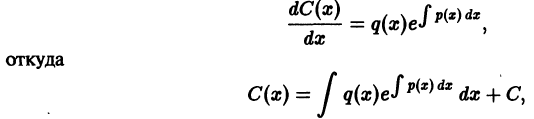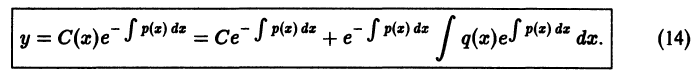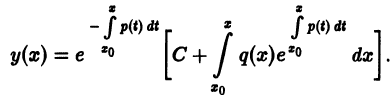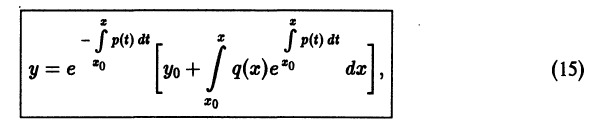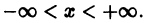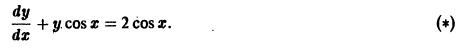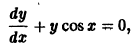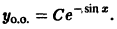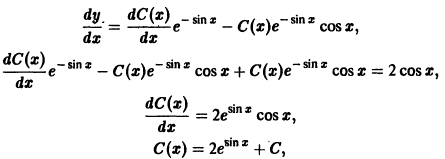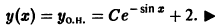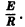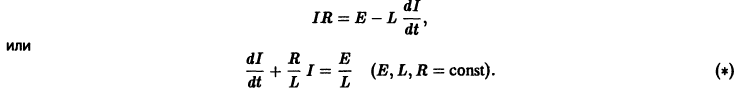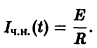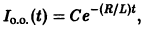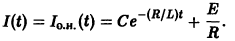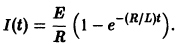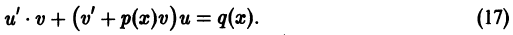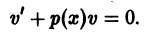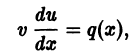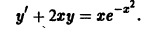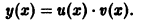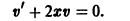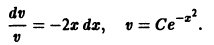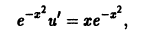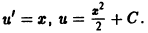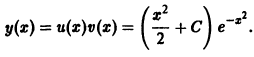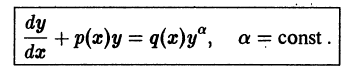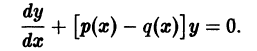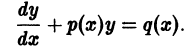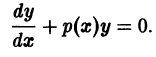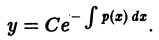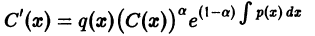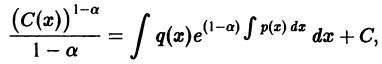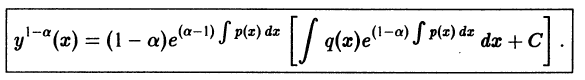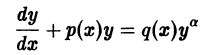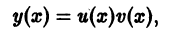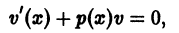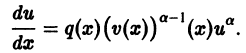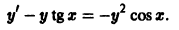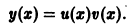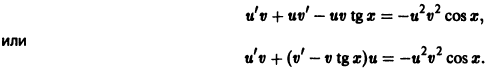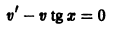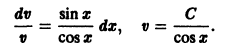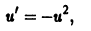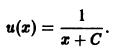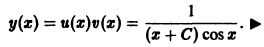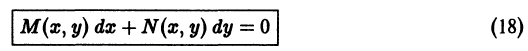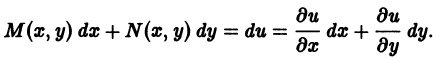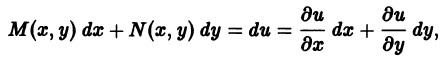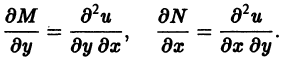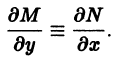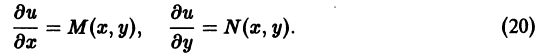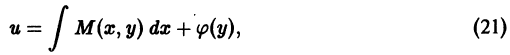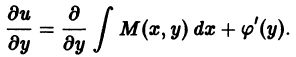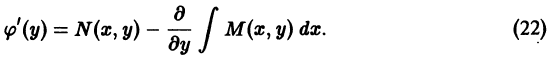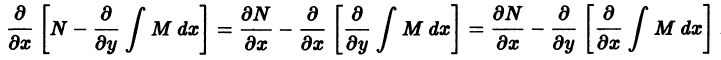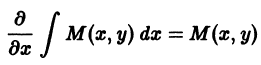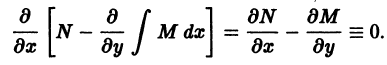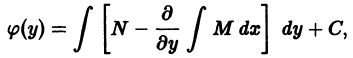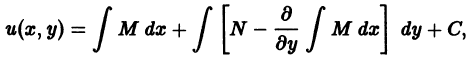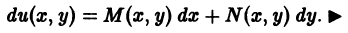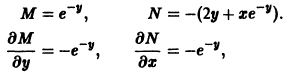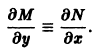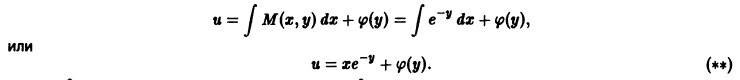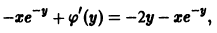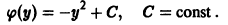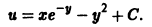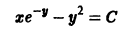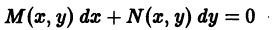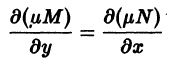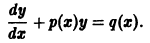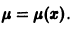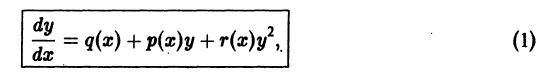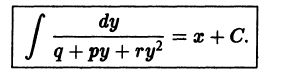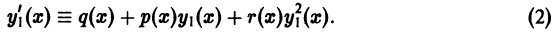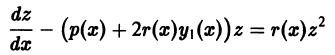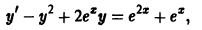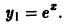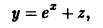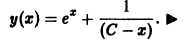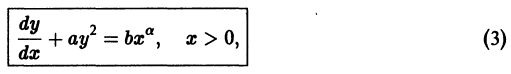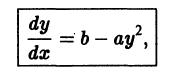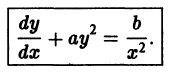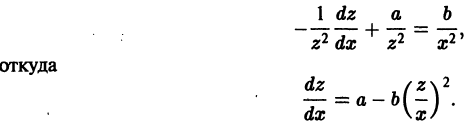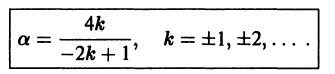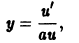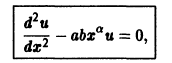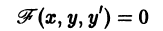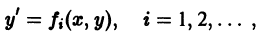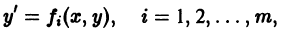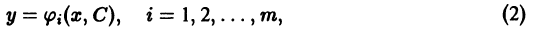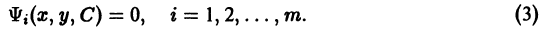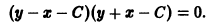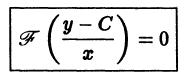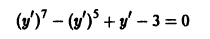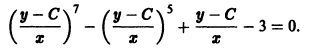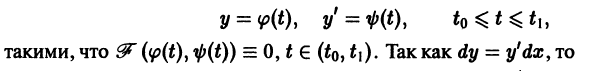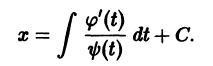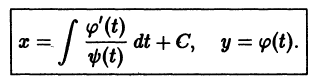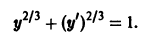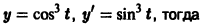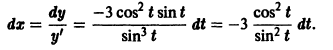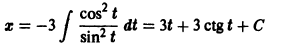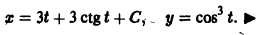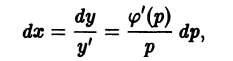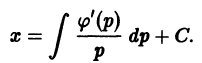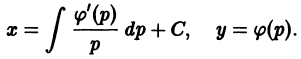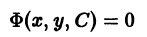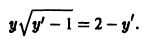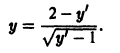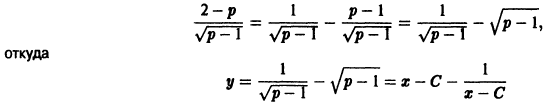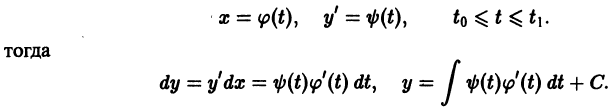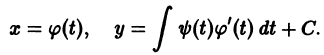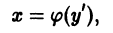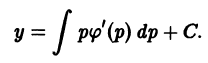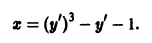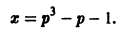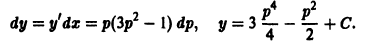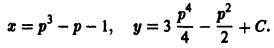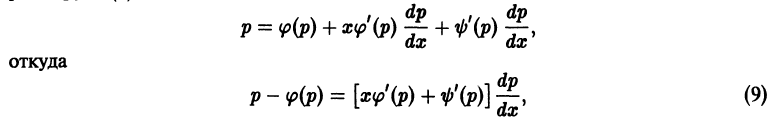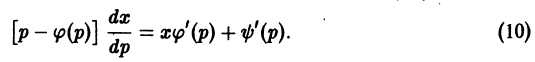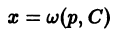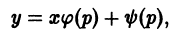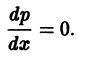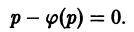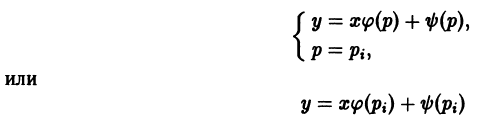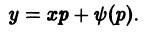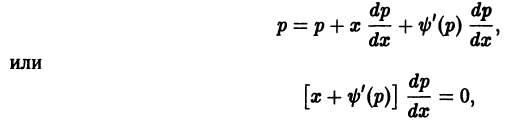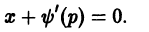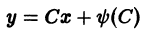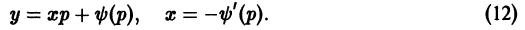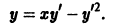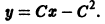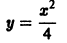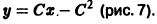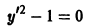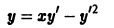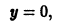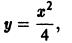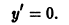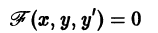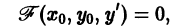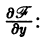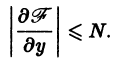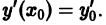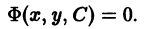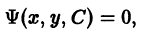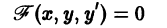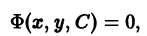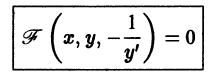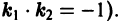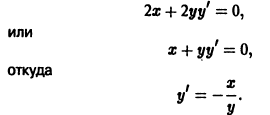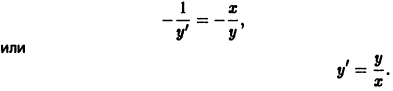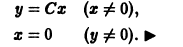Существует целый ряд задач, в которых установить прямую связь между величинами, применяемыми для описания процесса, не получается. Единственное, что можно сделать, это получить равенство, запись которого включает производные исследуемых функций, и решить его. Решение дифференциального уравнения позволяет установить непосредственную связь между величинами.
В этом разделе мы займемся разбором решений дифференциальных уравнений, неизвестная функция в которых является функцией одной переменной. Мы построили теоретическую часть таким образом, чтобы даже человек с нулевым представлением о дифференциальных уравнениях мог без труда получить необходимые знания и справиться с приведенными задачами.
Если какие-то термины окажутся для вас новыми, обратитесь к разделу «Определения и понятия теории дифференциальных уравнений». А тем временем перейдем к рассмотрению вопроса о видах дифференциальных уравнений.
Для каждого из видов дифференциальных уравнений применяется свой метод решения. В этом разделе мы рассмотрим все эти методы, приведем примеры с подробными разборами решения. После ознакомления с темой вам необходимо будет определять вид дифференциального уравнения и выбирать наиболее подходящий из методов решения поставленной задачи.
Возможно, прежде чем приступить к решению дифференциальных уравнений, вам придется освежить в памяти такие темы как «Методы интегрирования» и «Неопределенные интегралы».
Начнем ознакомление с темой мы с видов обыкновенных дифференциальных уравнений 1 -го порядка. Эти уравнения могут быть разрешены относительно производной. Затем перейдем в ОДУ 2 -го и высших порядков. Также мы уделим внимание системам дифференциальных уравнений.
Напомним, что y ‘ = d x d y , если y является функцией аргумента x .
- Дифференциальные уравнения первого порядка
- Простейшие дифференциальные уравнения первого порядка вида y ‘ = f ( x )
- Дифференциальные уравнения с разделяющимися переменными вида f 1 ( y ) · g 1 ( x ) d y = f 2 ( y ) · g 2 ( x ) d x или f 1 ( y ) · g 1 ( x ) · y ‘ = f 2 ( y ) · g 2 ( x )
- Линейные неоднородные дифференциальные уравнения первого порядка y ‘ + P ( x ) · y = Q ( x )
- Дифференциальное уравнение Бернулли y ‘ + P ( x ) y = Q ( x ) y a
- Уравнения в полных дифференциалах P ( x , y ) d x + Q ( x , y ) d y = 0
- Дифференциальные уравнения второго порядка
- Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами y ‘ ‘ + p y ‘ + q y = 0 , p , q ∈ R
- Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами y ‘ ‘ + p y ‘ + q y = f ( x ) , p , q ∈ R
- Линейные однородные дифференциальные уравнения (ЛОДУ) y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = 0 и линейные неоднородные дифференциальные уравнения (ЛНДУ) второго порядка y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = f ( x )
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения, допускающие понижение порядка
- Линейные однородные и неоднородные дифференциальные уравнения высших порядков с постоянными коэффициентами y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = 0 и y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = f ( x )
- Линейные однородные и неоднородные дифференциальные уравнения высших порядков y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 1 ( x ) · y ‘ + f 0 ( x ) · y = 0 и y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 1 ( x ) · y ‘ + f 0 ( x ) · y = f ( x )
- Системы дифференциальных уравнений вида d x d t = a 1 x + b 1 y + c 1 d y d t = a 2 x + b 2 y + c 2
- Методы интегрирования уравнений первого порядка
- Дифференциальные уравнения первого порядка с примерами решения и образцами выполнения
- Эквивалентные дифференциальные уравнения. Задача Коши
- Теорема существования и единственности решения задачи Коши для уравнения у’ = f(x, у)
- Приближенные методы интегрирования уравнения у’ = f(x, у)
- Метод изоклин
- Метод последовательных приближений
- Численные методы решения задачи Коши Метод Эйлера
- Понятие о методе Рунге—Кутта
- Некоторые виды уравнений, интегрируемых в квадратурах
- Уравнения с разделяющимися переменными
- Уравнения, однородные относительно x и у
- Линейные дифференциальные уравнения
- Уравнение Бернулли
- Уравнения в полных дифференциалах
- Уравнение Риккати
- Дифференциальные уравнения, не разрешенные относительно производной
- Уравнение Лагранжа
- Уравнение Клеро
- Геометрические вопросы, связанные с дифференциальными уравнениями 1-го порядка. Ортогональные траектории
- Ортогональные траектории
- Дополнение к дифференциальным уравнениям первого порядка
- 💡 Видео
Видео:7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

Дифференциальные уравнения первого порядка
Простейшие дифференциальные уравнения первого порядка вида y ‘ = f ( x )
Начнем с примеров таких уравнений.
y ‘ = 0 , y ‘ = x + e x — 1 , y ‘ = 2 x x 2 — 7 3
Оптимальным для решения дифференциальных уравнений f ( x ) · y ‘ = g ( x ) является метод деления обеих частей на f ( x ) . Решение относительно производной позволяет нам прийти к уравнению вида y ‘ = g ( x ) f ( x ) . Оно является эквивалентом исходного уравнения при f ( x ) ≠ 0 .
Приведем примеры подобных дифференциальных уравнений:
e x · y ‘ = 2 x + 1 , ( x + 2 ) · y ‘ = 1
Мы можем получить ряд дополнительных решений в тех случаях, когда существуют значения аргумента х , при которых функции f ( x ) и g ( x ) одновременно обращаются в 0 . В качестве дополнительного решения в уравнениях f ( x ) · y ‘ = g ( x ) при заданных значениях аргумента может выступать любая функция, определенная для заданного значения х .
Наличие дополнительных решений возможно для дифференциальных уравнений x · y ‘ = sin x , ( x 2 — x ) · y ‘ = ln ( 2 x 2 — 1 )
Ознакомиться с теоретической частью и примерами решения задач таких уравнений вы можете в разделе «Простейшие дифференциальные уравнения 1 -го порядка».
Дифференциальные уравнения с разделяющимися переменными вида f 1 ( y ) · g 1 ( x ) d y = f 2 ( y ) · g 2 ( x ) d x или f 1 ( y ) · g 1 ( x ) · y ‘ = f 2 ( y ) · g 2 ( x )
Поговорим теперь об уравнениях с разделенными переменными, которые имеют вид f ( y ) d y = g ( x ) d x . Как следует из названия, к данному виду дифференциальных уравнений относятся выражения, которые содержат переменные х и у , разделенные знаком равенства. Переменные находятся в разных частях уравнения, по обе стороны от знака равенства.
Решить уравнения с разделенными переменными можно путем интегрирования обеих его частей: ∫ f ( y ) d y = ∫ f ( x ) d x
К числу дифференциальных уравнений с разделенными переменными можно отнести следующие из них:
y 2 3 d y = sin x d x , e y d y = ( x + sin 2 x ) d x
Для того, чтобы прийти от ДУ с разделяющимися переменными к ДУ с разделенными переменными, необходимо разделить обе части уравнения на произведение f 2 ( y ) ⋅ g 1 ( x ) . Так мы придем к уравнению f 1 ( y ) f 2 ( y ) d y = g 2 ( x ) g 1 ( x ) d x . Преобразование можно будет считать эквивалентным в том случае, если одновременно f 2 ( y ) ≠ 0 и g 1 ( x ) ≠ 0 . Если хоть одно из условий не будет соблюдаться, мы можем потерять часть решений.
В качестве примеров дифференциальных уравнений с разделяющимися переменными можно привести следующие из них: d y d x = y · ( x 2 + e x ) , ( y 2 + a r c cos y ) · sin x · y ‘ = cos x y .
К уравнениям с разделяющимися переменными мы можем прийти от ряда дифференциальных уравнений других видов путем замены переменных. Например, мы можем подставить в исходное уравнение z = a x + b y . Это позволит нам перейти к дифференциальному уравнению с разделяющимися переменными от дифференциального уравнения вида y ‘ = f ( a x + b y ) , a , b ∈ R .
Подставив z = 2 x + 3 y в уравнение y ‘ = 1 e 2 x + 3 y получаем d z d x = 3 + 2 e z e z .
Заменив z = x y или z = y x в выражениях y ‘ = f x y или y ‘ = f y x , мы переходим к уравнениям с разделяющимися переменными.
Если произвести замену z = y x в исходном уравнении y ‘ = y x · ln y x + 1 , получаем x · d z d x = z · ln z .
В ряде случаев прежде, чем производить замену, необходимо произвести преобразования исходного уравнения.
Предположим, что в условии задачи нам дано уравнение y ‘ = y 2 — x 2 2 x y . Нам необходимо привести его к виду y ‘ = f x y или y ‘ = f y x . Для этого нам нужно разделить числитель и знаменатель правой части исходного выражения на x 2 или y 2 .
Нам дано уравнение y ‘ = f a 1 x + b 1 y + c 1 a 2 x + b 2 y + c 2 , a 1 , b 1 , c 1 , a 2 , b 2 , c 2 ∈ R .
Для того, чтобы привести исходное уравнение к виду y ‘ = f x y или y ‘ = f y x , нам необходимо ввести новые переменные u = x — x 1 v = y — y 1 , где ( x 1 ; y 1 ) является решением системы уравнений a 1 x + b 1 y + c 1 = 0 a 2 x + b 2 y + c 2 = 0
Введение новых переменных u = x — 1 v = y — 2 в исходное уравнение y ‘ = 5 x — y — 3 3 x + 2 y — 7 позволяет нам получить уравнение вида d v d u = 5 u — v 3 u + 2 v .
Теперь выполним деление числителя и знаменателя правой части уравнения на u . Также примем, что z = u v . Получаем дифференциальное уравнение с разделяющимися переменными u · d z d u = 5 — 4 z — 2 z 2 3 + 2 z .
Подробный разбор теории и алгоритмов решения задач мы привели в разделе «Дифференциальные уравнения с разделяющимися переменными».
Линейные неоднородные дифференциальные уравнения первого порядка y ‘ + P ( x ) · y = Q ( x )
Приведем примеры таких уравнений.
К числу линейных неоднородных дифференциальных уравнений 1 -го порядка относятся:
y ‘ — 2 x y 1 + x 2 = 1 + x 2 ; y ‘ — x y = — ( 1 + x ) e — x
Для решения уравнений этого вида применяется метод вариации произвольной постоянной. Также мы можем представить искомую функцию у в виде произведения y ( x ) = u ( x ) v ( x ) . Алгоритмы применения обоих методов мы привели в разделе «Линейные неоднородные дифференциальные уравнения первого порядка».
Дифференциальное уравнение Бернулли y ‘ + P ( x ) y = Q ( x ) y a
Приведем примеры подобных уравнений.
К числу дифференциальных уравнений Бернулли можно отнести:
y ‘ + x y = ( 1 + x ) e — x y 2 3 ; y ‘ + y x 2 + 1 = a r c t g x x 2 + 1 · y 2
Для решения уравнений этого вида можно применить метод подстановки z = y 1 — a , которая выполняется для того, чтобы свести исходное уравнение к линейному дифференциальному уравнению 1 -го порядка. Также применим метод представления функции у в качестве y ( x ) = u ( x ) v ( x ) .
Алгоритм применения обоих методов приведен в разделе «Дифференциальное уравнение Бернулли». Там же можно найти подробный разбор решения примеров по теме.
Уравнения в полных дифференциалах P ( x , y ) d x + Q ( x , y ) d y = 0
Если для любых значений x и y выполняется ∂ P ( x , y ) ∂ y = ∂ Q ( x , y ) ∂ x , то этого условия необходимо и достаточно, чтобы выражение P ( x , y ) d x + Q ( x , y ) d y представляло собой полный дифференциал некоторой функции U ( x , y ) = 0 , то есть, d U ( x , y ) = P ( x , y ) d x + Q ( x , y ) d y . Таким образом, задача сводится к восстановлению функции U ( x , y ) = 0 по ее полному дифференциалу.
Выражение, расположенное в левой части записи уравнения ( x 2 — y 2 ) d x — 2 x y d y = 0 представляет собой полный дифференциал функции x 3 3 — x y 2 + C = 0
Для более подробного ознакомления с теорией и алгоритмами решения примеров можно обратиться к разделу «Уравнения в полных дифференциалах».
Видео:Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать

Дифференциальные уравнения второго порядка
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами y ‘ ‘ + p y ‘ + q y = 0 , p , q ∈ R
Линейное однородное дифференциальное уравнение с постоянными коэффициентами обычно решается достаточно просто. Нам необходимо найти корни характеристического уравнения k 2 + p k + q = 0 . Здесь возможны три варианта в зависимости от различных p и q :
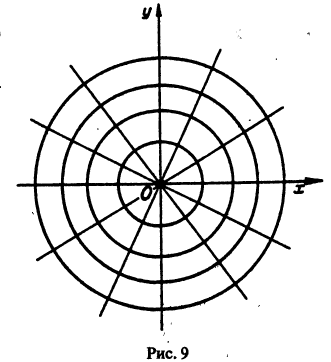
- действительные и различающиеся корни характеристического уравнения k 1 ≠ k 2 , k 1 , k 2 ∈ R ;
- действительные и совпадающие k 1 = k 2 = k , k ∈ R ;
- комплексно сопряженные k 1 = α + i · β , k 2 = α — i · β .
Значения корней характеристического уравнения определяет, как будет записано общее решение дифференциального уравнения. Возможные варианты:
- y = C 1 e k 1 x + C 2 e k 2 x ;
- y = C 1 e k x + C 2 x e k x ;
- y = e a · x · ( C 1 cos β x + C 2 sin β x ) .
Пример 13
Предположим, что у нас есть линейное однородное дифференциальное уравнение 2 -го порядка с постоянными коэффициентами y ‘ ‘ + 3 y ‘ = 0 . Найдем корни характеристического уравнения k 2 + 3 k = 0 . Это действительные и различные k 1 = — 3 и k 2 = 0 . Это значит, что общее решение исходного уравнения будет иметь вид:
y = C 1 e k 1 x + C 2 e k 2 x ⇔ y = C 1 e — 3 x + C 2 e 0 x ⇔ y = C 1 e — 3 x + C 2
Восполнить пробелы в теоретической части и посмотреть подробный разбор примеров по теме можно в статье «Линейные однородные дифференциальные уравнения 2 -го порядка с постоянными коэффициентами».
Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами y ‘ ‘ + p y ‘ + q y = f ( x ) , p , q ∈ R
Основным способом решение уравнений данного вида является нахождение суммы общего решения y 0 , которое соответствует линейному однородному дифференциальному уравнению y ‘ ‘ + p y ‘ + q y = 0 , и частного решения y
исходного уравнения. Получаем: y = y 0 + y
Способ нахождения y 0 мы рассмотрели в предыдущем пункте. Найти частное решение y
мы можем методом неопределенных коэффициентов при определенном виде функции f ( x ) , которая расположена в правой части записи исходного выражения. Также применим метод вариации произвольных постоянных.
К числу линейных неоднородных дифференциальных уравнений 2 -го порядка с постоянными коэффициентами относятся:
y ‘ ‘ — 2 y ‘ = ( x 2 + 1 ) e x ; y ‘ ‘ + 36 y = 24 sin ( 6 x ) — 12 cos ( 6 x ) + 36 e 6 x
Теоретические выкладки и подробный разбор примеров по теме можно найти в разделе «ЛНДУ 2 -го порядка с постоянными коэффициентами».
Линейные однородные дифференциальные уравнения (ЛОДУ) y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = 0 и линейные неоднородные дифференциальные уравнения (ЛНДУ) второго порядка y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = f ( x )
Линейные однородные и неоднородные дифференциальные уравнения и постоянными коэффициентами являются частными случаями дифференциальных уравнений этого вида.
На некотором отрезке [ a ; b ] общее решение линейного однородного дифференциального уравнения y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = 0 представлено линейной комбинацией двух линейно независимых частных решений y 1 и y 2 этого уравнения, то есть, y = C 1 y 1 + C 2 y 2 .
Частные решения мы можем выбрать из систем независимых функций:
1 ) 1 , x , x 2 , . . . , x n 2 ) e k 1 x , e k 2 x , . . . , e k n x 3 ) e k 1 x , x · e k 1 x , . . . , x n 1 · e k 1 x , e k 2 x , x · e k 2 x , . . . , x n 2 · e k 2 x , . . . e k p x , x · e k p x , . . . , x n p · e k p x 4 ) 1 , c h x , s h x
Однако существуют примеру уравнений, для которых частные решения не могут быть представлены в таком виде.
Возьмем для примера линейное однородное дифференциальное уравнение x y ‘ ‘ — x y ‘ + y = 0 .
Общее решение линейного неоднородного дифференциального уравнения y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = f ( x ) мы можем найти в виде суммы y = y 0 + y
, где y 0 — общее решение соответствующего ЛОДУ, а y
частное решение исходного дифференциального уравнения. Найти y 0 можно описанным выше способом. Определить y
нам поможет метод вариации произвольных постоянных.
Возьмем для примера линейное неоднородное дифференциальное уравнение x y ‘ ‘ — x y ‘ + y = x 2 + 1 .
Более подробно этот раздел освещен на странице «Линейные дифференциальные уравнения второго порядка».
Видео:13. Как решить дифференциальное уравнение первого порядка?Скачать
Дифференциальные уравнения высших порядков
Дифференциальные уравнения, допускающие понижение порядка
Мы можем провести замену y ( k ) = p ( x ) для того, чтобы понизить порядок исходного дифференциального уравнения F ( x , y ( k ) , y ( k + 1 ) , . . . , y ( n ) ) = 0 , которое не содержит искомой функции и ее производных до k — 1 порядка.
В этом случае y ( k + 1 ) = p ‘ ( x ) , y ( k + 2 ) = p ‘ ‘ ( x ) , . . . , y ( n ) = p ( n — k ) ( x ) , и исходное дифференциальное уравнение сведется к F 1 ( x , p , p ‘ , . . . , p ( n — k ) ) = 0 . После нахождения его решения p ( x ) останется вернуться к замене y ( k ) = p ( x ) и определить неизвестную функцию y .
Дифференциальное уравнение y ‘ ‘ ‘ x ln ( x ) = y ‘ ‘ после замены y ‘ ‘ = p ( x ) станет уравнением с разделяющимися переменными y ‘ ‘ = p ( x ) , и его порядок с третьего понизится до первого.
В уравнении, которое не содержит аргумента х и имеет вид F ( y , y ‘ , y ‘ ‘ , . . . , y ( n ) ) = 0 , порядок может быть заменен на единицу следующим образом: необходимо провести замену d y d x = p ( y ) , где p ( y ( x ) ) будет сложной функцией. Применив правило дифференцирования, получаем:
d 2 y d x 2 = d p d y d y d x = d p d y p ( y ) d 3 y d x 3 = d d p d y p ( y ) d x = d 2 p d y 2 d y d x p ( y ) + d p d y d p d y d y d x = = d 2 p d y 2 p 2 ( y ) + d p d y 2 p ( y )
Полученный результаты подставляем в исходное выражение. При этом мы получим дифференциальное уравнение, порядок которого на единицу меньше, чем у исходного.
Рассмотрим решение уравнения 4 y 3 y ‘ ‘ = y 4 — 1 . Путем замены d y d x = p ( y ) приведем исходное выражение к уравнению с разделяющимися переменными 4 y 3 p d p d y = y 4 — 1 .
Более подробно решения задач по теме рассмотрены в разделе «Дифференциальные уравнения, допускающие понижение порядка».
Линейные однородные и неоднородные дифференциальные уравнения высших порядков с постоянными коэффициентами y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = 0 и y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = f ( x )
Решение уравнений данного вида предполагает выполнение следующих простых шагов:
- находим корни характеристического уравнения k n + f n — 1 · k n — 1 + . . . + f 1 · k + f 0 = 0 ;
- записываем общее решение ЛОДУ y 0 в стандартной форме, а общее решение ЛНДУ представляем суммой y = y 0 + y
— частное решение неоднородного дифференциального уравнения.
Нахождение корней характеристического уравнения подробно описано в разделе «Решение уравнений высших степеней». Для нахождения y
целесообразно использовать метод вариации произвольных постоянных.
Линейному неоднородному ДУ с постоянными коэффициентами y ( 4 ) + y ( 3 ) — 5 y ‘ ‘ + y ‘ — 6 y = x cos x + sin x соответствует линейное однородное ДУ y ( 4 ) + y ( 3 ) — 5 y ‘ ‘ + y ‘ — 6 y = 0 .
Более детальный разбор теории и примеров по теме вы можете найти на странице « Линейные однородные и неоднородные дифференциальные уравнения высших порядков с постоянными коэффициентами».
Линейные однородные и неоднородные дифференциальные уравнения высших порядков y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 1 ( x ) · y ‘ + f 0 ( x ) · y = 0 и y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 1 ( x ) · y ‘ + f 0 ( x ) · y = f ( x )
Найти решение ЛНДУ высших порядков можно благодаря сумме y = y 0 + y
, где y 0 — общее решение соответствующего ЛОДУ, а y
— частное решение неоднородного дифференциального уравнения.
y 0 представляет собой линейную комбинацию линейно независимых функций y 1 , y 2 , . . . , y n , каждая из которых является частным решением ЛОДУ, то есть, обращает равенство y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 1 ( x ) · y ‘ + f 0 ( x ) · y = 0 в тождество. Частные решения y 1 , y 2 , . . . , y n обычно подбираются из известных систем линейно независимых функций. Подобрать их далеко не всегда просто и возможно, в этом и заключается основная проблема.
После того, как мы найдем общее решение ЛОДУ, найти частное решение соответствующего ЛНДУ можно благодаря методу вариации произвольных постоянных. Итак, y = y 0 + y
Получить более подробную информацию по теме можно в разделе «Дифференциальные уравнения высших порядков».
Видео:Интеграл: Азы интегрирования. Высшая математикаСкачать

Системы дифференциальных уравнений вида d x d t = a 1 x + b 1 y + c 1 d y d t = a 2 x + b 2 y + c 2
Данная тема подробно разобрана на странице «Системы дифференциальных уравнений». Там же приведены примеры задач с подробных разбором.
Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Методы интегрирования уравнений первого порядка
1. У равнения с разделяющимися переменными
Общий вид уравнений
С учетом равенства
уравнение (8.10) может быть записано в виде 
Разделим обе части на произведение функций M ( x )∙ Q ( y ) (при условии 



Пример 8.2. Проинтегрировать уравнение 
Решение . Представим уравнение в виде 

После применения теоремы о сумме логарифмов и потенцирования получаем
2. Однородные дифференциальные уравнения первого порядка
Общий вид уравнений
где M ( x ; y ) и N ( x ; y )– однородные функции аргументов x и y одного и того же измерения m , то есть имеют место равенства
Метод решения уравнения (8.12) – деление на переменную x в степени измерения m : 
Однородное уравнение (8.12) принимает вид: 
Пример 8.3. Проинтегрировать уравнение 
Решение. Поделим уравнение на x 2 , получим 




Пример 8.4. Найти общее решение (общий интеграл) дифференциального уравнения 
Решение . Правая часть уравнения 






После интегрирования обеих частей уравнения получаем
Потенцируя, находим 
Итак, общий интеграл исходного уравнения приобретает вид cy = x 2 + y 2 , где c – произвольная постоянная
3. Дифференциальные уравнения первого порядка, приводящиеся к однородным или к уравнениям с разделяющимися переменными
Общий вид уравнений
где 
При c 1 = c 2 = 0 уравнение является однородным. Рассмотрим два случая при c 1 и c 2 не равных нулю одновременно.
1) Определитель 

В результате данной подстановки уравнение (8.15) становится однородным.
Пример 8.5. Найти общее решение (общий интеграл) дифференциального уравнения 
Решение . Определитель 



С помощью формул интегрирования (4.8) и (4.17) получаем:
Осуществим обратную подстановку 

2) Определитель 

Пример 8.6. Найти общее решение (общий интеграл) дифференциального уравнения
Решение . Определитель 
Исходное уравнение принимает вид:
Далее 


После обратной замены получим: 
4. Линейные дифференциальные уравнения первого порядка
Общий вид уравнений
где P ( x ) и Q ( x ) – заданные функции (могут быть постоянными).
Уравнение (8.16) может быть решено двумя способами.
1) Метод Бернулли-Фурье состоит в том, что решение ищется в виде произведения двух неизвестных функций y ( x )= u ( x )∙ v ( x ) или коротко y = u ∙ v , при этом 

Функцию v ( x ) подберем в частном виде так, чтобы выражение в скобках обратилось в ноль. Для этого решим уравнение с разделяющимися переменными 





Пример 8.7. Проинтегрировать уравнен ие 
Решение . Данное уравнение является линейным ДУ первого порядка с функциями 

Выберем функцию u так, чтобы выражение, стоящее в скобках, обращалось в ноль, то есть 
Полагая c = 1, получим u = cos x . При таком выборе функции u уравнение (**) примет вид:


Общее решение заданного ДУ можно также получить, пользуясь непосредственно формулой (8.18):
По условию задачи имеем: P ( x )= tg x , 


Таким образом, 
2) Метод Лагранжа иначе называют методом вариации произвольной постоянной. Рассмотрим сначала соответствующее линейное однородное ДУ первого порядка, то есть исходное уравнение без правой части 

Пример 8.8. Проинтегрировать уравнение 
Решение . Решим сначала соответствующее линейное однородное ДУ первого порядка 





Подставляя найденное c ( x ) в y , имеем общее решение линейного неоднородного уравнения:
5. Уравнения Бернулли
Общий вид уравнений
При n = 1 (8.1 9) – уравнение с разделяющимися переменными. При n = 0 (8.1 9) – линейное ДУ.
Рассмотрим 


то есть его решение находится аналогично пункту 4. На практике искать решение уравнения (8.17) удобнее методом Бернулли в виде произведения неизвестных функций y = u ∙ v . Заметим, что y = 0 – всегда является решением исходного уравнения (8.17).
Пример 8.9. Проинтегрировать уравнение 
Решение. Заданное уравнение является уравнением Бернулли. Положим y = u ∙ v , тогда 
Выберем функцию u так, чтобы выполнялось равенство: 
Тогда заданное уравнение после сокращения на u примет вид: 



6. Уравнения в полных дифференциалах
6.1. Общий вид уравнений
где левая часть есть полный дифференциал некоторой функции F ( x ; y ), то есть 

Условие, по которому можно судить, что выражение 
Теорема 8.2. Для того чтобы выражение 



Таким образом, согласно определению полного дифференциала (6.6) должны выполняться равенства:
Формула (8.22) представляет собой теорему Шварца, согласно которой смешанные производные второго порядка функции F ( x ; y ) равны.
Зафиксируем переменную y и проинтегрируем первое уравнение из (8.23) по x , получим:
Здесь мы применили метод вариации произвольной постоянной, так как предположили, что константа c зависит от y (либо является числом). Продифференцировав (8.24) по переменной y и приравняв производную к функции N ( x ; y ), мы получим уравнение для нахождения неизвестной c ( y ). Подставив c ( y ) в (8.24), находим функцию F ( x ; y ) такую, что 
Пример 8.10. Решить уравнение 
Решение. Здесь функция 
Проверим условие (8.22): 
Пусть c = c ( y ), тогда 


Найденное c ( y ) подставляем в функцию F ( x ; y ), получаем решение заданного ДУ:
Если условие (8.22) не выполняется, то ДУ (8.21) не является уравнением в полных дифференциалах.
Однако это уравнение иногда можно привести к уравнению в полных дифференциалах умножением его на некоторую функцию μ ( x ; y ), называемую интегрирующим множителем .
Чтобы уравнение 
Выполнив дифференцирование 

6.2. Пусть μ = μ ( x ). Тогда уравнение (8.25) принимает вид:
При этом подынтегральное выражение должно зависеть только от x.
6.3. Пусть μ = μ ( y ). Тогда аналогично можно получить
где подынтегральное выражение должно зависеть только от y .
Пример 8.11. Решить уравнение 
Решение . Здесь 

7. Дифференциальные уравнения, не разрешенные относительно производной
К уравнениям данного вида относятся уравнения Лагранжа и Клеро, которые образуют достаточно большой класс ДУ, решаемых методом введения параметра 
7.1. Уравнение Лагранжа
Общий вид уравнений
где φ и ψ– известные функции от 

Продифференцируем его по x :
Полученное уравнение (8.30) является линейным уравнением относительно неизвестной функции x = x ( p ). Решив его, найдем:
Исключая параметр p из уравнений (8.29) и (8.31), получаем общий интеграл уравнения (8.28) в виде y = γ ( x ; c ).
Примечание. При переходе к уравнению (8.30) мы делили на 


7.2. Уравнение Клеро представляет собой частный случай уравнения Лагранжа при 

Вводим параметр 
Продифференцируем уравнение (8.33) по переменной x:
При 
Это – особое решение уравнения Клеро, так как оно не содержится в формуле общего решения уравнения.
Пример 8.12. Решить уравнение Клеро 
Решение. Согласно формуле (8.32) общее решение имеет вид y = cx + c 2 . Особое решение уравнения получим по (8.33) в виде 

Видео:Асташова И. В. - Дифференциальные уравнения I - Методы интегрирования уравнений первого порядкаСкачать

Дифференциальные уравнения первого порядка с примерами решения и образцами выполнения
Обыкновенным дифференциальным уравнением называется уравнение вида
связывающее независимую переменную х, искомую функцию у = у(х) и ее производные у'(х), у»(х), … , 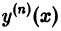
Замечание:
Обозначения зависимой и независимой переменных через х и у, используемые в приведенном определении, не являются жесткими; часто в качестве независимой удобно брать переменную t, иными буквами обозначают и зависимую переменную (см. ниже пример 2).
В обыкновенном дифференциальном уравнении искомая функция у = у(х) есть функция одной независимой переменной x. Если искомая функция есть функция двух (и более) независимых переменных, то имеем дифференциальное уравнение с частными производными. В этой и двух следующих главах мы будем рассматривать только обыкновенные дифференциальные уравнения.
Простейшим дифференциальным уравнением является уравнение вида
где f(x) — известная непрерывная на некотором интервале (а, b) функция, а у = у(х) — искомая функция. С таким уравнением мы уже встречались в интегральном исчислении, когда поданной функции f(x) требовалось найти ее первообразную F(x). Как известно, всякая функция, удовлетворяющая уравнению (2), имеет вид
где F(x) — какая-нибудь первообразная для функции f(x) на интервале (а, Ь), а С — произвольная постоянная. Таким образом, искомая функция у = у(х) определяется из уравнения (2) неоднозначно.
Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение. Например,
— дифференциальное уравнение 1-го порядка;
— дифференциальное уравнение 2-го порядка;
— дифференциальное уравнение пятого порядка.
Решением дифференциального уравнения n-го порядка на интервале (а, b) называется всякая функция 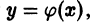
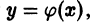
Например, функция у = sin х является решением дифференциального уравнения второго порядка
на интервале 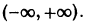
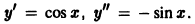
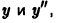
Задача:
Найти совпадающие решения двух дифференциальных уравнений (не решая самих уравнений):
График решения дифференциального уравнения называется интегральной кривой этого уравнения.
Процесс нахождения решения дифференциального уравнения называется интегрированием дифференциального уравнения. К составлению и интегрированию дифференциальных уравнений приводят многочисленные задачи как самой математики, так и других наук (физики, химии, биологии и т. п.).
Пример:
Найти такую кривую, чтобы тангенс угла наклона касательной в каждой ее точке численно равнялся ординате точки касания.
— уравнение искомой кривой. Как известно, tg а = у'(х) и, значит, определяющее свойство кривой есть
— дифференциальное уравнение первого порядка. Нетрудно видеть, что функция
Есть решение этого уравнения. Оно также имеет очевидное решение у = 0. Кроме того, решениями будут функции
где С — произвольная постоянная, так что уравнение имеет бесконечное множество решений.
Пример:
Найти закон прямолинейного движения материальной точки, движущейся с постоянным ускорением а.
Требуется найти формулу 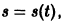
— дифференциальное уравнение второго порядка. Последовательно находим:
Произвольные постоянные можно определить, если положить
В самом деле, полагая t = to в первом из соотношений (*), получаем 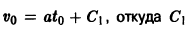
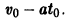
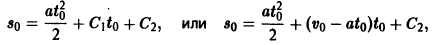
Подставляя найденные значения C1 и С2 в выражение для функции s(t), приходим к известному закону движения материальной точки с постоянным ускорением:
Видео:Математика без ху!ни. Интегралы, часть 1. Первообразная. Дифференцирование и интегрирование.Скачать

Эквивалентные дифференциальные уравнения. Задача Коши
Пусть имеем дифференциальное уравнение первого порядка
Если в этом уравнении удается выразить производную у’ через х и у, то получаем уравнение
разрешенное относительно производной. Здесь f — заданная функция своих аргументов.
Наряду с уравнением (1) рассматривают эквивалентное ему дифференциальное уравнение
или уравнение более общего вида
получаемое из (1′) путем умножения на некоторую функцию 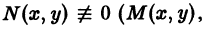
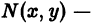
Два дифференциальных уравнения
называются эквивалентными в некоторой области D изменения величин х, у, у’, если всякое решение 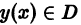
Если дифференциальное уравнение имеет решение, то, как правило, множество его решений оказывается бесконечным. Впрочем, дифференциальное уравнение
имеет только одно решение
y = х,
вообще не имеет действительных решений.
Чтобы выделить определенное решение уравнения (1), надо задать начальное условие, которое заключается в том, что при некотором значении Xо независимой переменной х заранее дано значение Yo искомой функции у(х):
Геометрически это означает, что задается точка 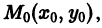
Задачу отыскания решения у(х) уравнения (1), удовлетворяющего начальному условию (2), называют задачей Коши (начальной задачей) для уравнения (1).
Теорема существования и единственности решения задачи Коши для уравнения у’ = f(x, у)
Теорема:
Существования и единственности решения. Пусть имеем дифференциальное уравнение
и пусть функция f(x,y) определена в некоторой области D на плоскости хОу. Выберем произвольную точку 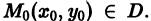
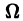
1) непрерывна по совокупности аргументов;
2) имеет ограниченную частную производную 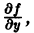
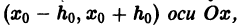
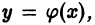
Геометрически это означает, что через точку 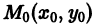
Теорема 1 имеет локальный характер: она гарантирует существование единственного решения 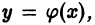
Пример:
у’ = х + у
f(x,y) = x + у
определена и непрерывна во всех точках плоскости хОу и имеет всюду 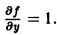
Пример:
определена и непрерывна на всей плоскости хОу. Здесь
так что второе условие теоремы 1 нарушается в точках оси Ох. Нетрудно проверить, что функция
где С — любая постоянная, является решением данного уравнения. Кроме того, уравнение имеет очевидное решение
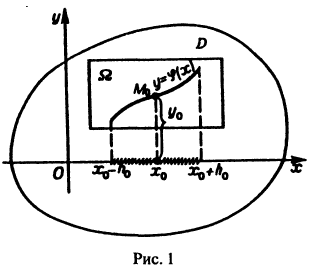
Если искать решения этого уравнения, соответствующие условию у(0) = 0, то таких решений найдется бесчисленное множество, а частности, следующие (рис. 2):
Таким образом, через каждую точку оси Ох проходят по крайней мере две интегральные кривые и, следовательно, в точках Этой оси нарушается единственность.
Если взять точку М1 (1,1), то в достаточно малой ее окрестности выполнены все условия теоремы 1. Следовательно, через данную точку в малом квадрате 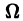
уравнения 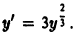
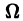
Теорема 1 дает достаточные условия существования единственного решения уравнения у’ = f(x,y). Это означает, что может существовать единственное решение у = у(х) уравнения у’ = f(x, у), удовлетворяющее условию 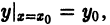
Пример:
В точках оси Ох функции 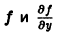
Но через каждую точку (Хо, 0) оси Ох проходит единственная интегральная кривая
Замечание:
Если отказаться от ограниченности 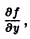
Теорема:
Если функция f(x, у) непрерывна в некоторой окрестности точки (х0, уо), то уравнение у’ = f(x, у) имеет в этой окрестности по крайней мере одно решение 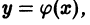
Задача:
Найти интегральную кривую уравнения
проходящую через точку О (0,0).
Задача:
Найти решение задачи Коши
Определение:
Общим решением дифференциального уравнения
в некоторой области 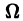
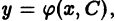
1) при любом допустимом значении постоянной С функция 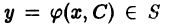
2) каково бы ни было начальное условие 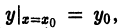
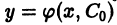
При этом предполагается, что точка (Хо, Уо) принадлежит области 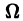
Пример:
Показать, что общим решением дифференциального уравнения
у’ = 1
у = х + С,
где С — произвольная постоянная.
В данном случае f(x, у) = 1, и условия теоремы 1 выполняются всюду. Следовательно, через каждую точку (Хо, Уо) плоскости хОу проходит единственная интегральная кривая данного уравнения.
Проверим, что функция
у = х + С
удовлетворяет условиям 1) и 2), содержащимся в определении общего решения. Действительно, при любом С имеем
у’ = (х + С)’ = 1,
так что у = х + С есть решение данного уравнения. Потребовав, чтобы при Х = Хо решение принимало значение Уо, приходим к соотношению Уо = Хо + Со. откуда
Решение у = х + Уо — Хо, или
удовлетворяет поставленному начальному условию.
Частным решением дифференциального уравнения (1) называется решение, получаемое из общего при каком-либо конкретном значении произвольной постоянной С (включая 
В процессе интегрирования дифференциального уравнения мы часто приходим к уравнению
неявно задающему общее решение уравнения. Уравнение (2) называют общим интегралом дифференциального уравнения (1).
где 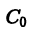
Замечание:
Название происходит от того, что для простейшего дифференциального уравнения вида
его общее решение действительно записывается при помощи обычного неопределенного интеграла
Пример:
Общий интеграл уравнения
имеет следующий вид
В дальнейшем для краткости мы будем иногда говорить, что решение уравнения проходит через некоторую точку 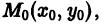
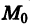
Определение:
дифференциального уравнения (1) называется особым, если в каждой его точке нарушается свойство единственности, т. е. если через каждую его точку 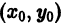
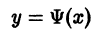
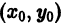
График особого решения называют особой интегральной кривой уравнения. Геометрически это — огибающая семейства интегральных кривых дифференциального уравнения, определяемых его общим интегралом.
Если для дифференциального уравнения (1) в некоторой области D на плоскости хОу выполнены условия теоремы 1, то через каждую точку 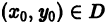
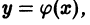
образующих общий интеграл уравнения (1), и получается из этого семейства при конкретном значении параметра С, т.е. является частным интегралом уравнения (1). Никаких других решений, проходящих через точку 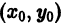
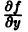
Напомним, что огибающей семейства кривых 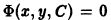
Например, для уравнения
функция 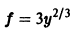
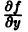
— семейство кубических парабол — и очевидное решение
проходящее через те точки, где производная 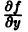
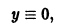
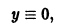
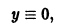
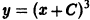

Из теоремы 1 можно вывести только необходимые условия для особого решения. Множество тех точек, где производная 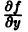
то в точках прямой у = 0 по-прежнему нарушается условие ограниченности производной 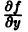
Итак, чтобы найти особые решения уравнения (1), надо
1) найти множество точек, где производная 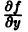
2) если это множество точек образует одну или несколько кривых, проверить, являются ли они интегральными кривыми уравнения (1);
3) если это интегральные кривые, проверить, нарушается ли в каждой их точке свойство единственности.
При выполнении всех этих условий найденная кривая представляет собой особое решение уравнения (1).
Задача:
Найти особые решения уравнения
Видео:Методы интегрирования. 11 класс.Скачать

Приближенные методы интегрирования уравнения у’ = f(x, у)
Метод изоклин
Пусть имеем дифференциальное уравнение
где функция f(x, у) в некоторой области D на плоскости хОу удовлетворяет условиям теоремы 1. Это уравнение определяет в каждой точке (х, у) области D значение у’, т. е. угловой коэффициент касательной к интегральной кривой в этой точке. Говорят, что уравнение (1) определяет в области D поле направлений. Чтобы его построить, надо в каждой точке 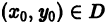
Совокупность этих отрезков дает геометрическую картину поля направлений. Задача интегрирования дифференциального уравнения (1) может быть теперь сформулирована так: найти такую кривую, чтобы касательная к ней в каждой точке имела направление, совпадающее с направлением поля в этой точке. Такое истолкование дифференциального уравнения и его интегрирования дает графический способ решения уравнения.
Для построения интегральных кривых пользуются изоклинами. Изоклиной называется множество всех точек плоскости хОу, в которых касательные к искомым интегральным кривым имеют одно и то же направление (у’ = const).
Из этого определения следует, что семейство изоклин дифференциального уравнения (1) задается уравнением
где к — числовой параметр. Если придать параметру к близкие числовые значения, можно найти достаточно густую сеть изоклин и приближенно построить интегральные кривые дифференциального уравнения.
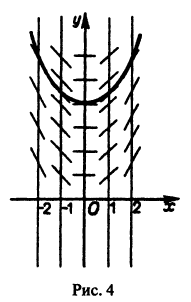
Пример:
по способу изоклин.
Семейство изоклин данного уравнения определяется уравнением
Полагая к = 0, + 1, — 1,…, получаем изоклины
по которым строим интегральные кривые уравнения (рис. 4).
определяет множество возможных точек экстремума интегральных кривых (прямая x = 0 в примере 1).
Для большей точности построения интегральных кривых определяют направление вогнутости и точки перегиба этих кривых (если такие точки существуют). Для этого находят у» в силу уравнения (1):
Знак правой части определяет знак у», т. е. направление вогнутости интегральных кривых. Линия, заданная уравнением
есть множество всех возможных точек перегиба интегральных кривых.
В примере 1 имеем
поэтому все интегральные кривые обращены вогнутостью вверх, и точек перегиба интегральных кривых нет.
Метод последовательных приближений
Пусть имеем дифференциальное уравнение
где функция f(x, у) в некоторой области D изменения х, у удовлетворяет условиям теоремы 1, и пусть точка 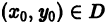
равносильно решению некоторого интегрального уравнения, т. е. уравнения, в которое неизвестная функция входит под знаком интеграла. В самом деле, пусть
— решение уравнения (2), заданное в некоторой окрестности 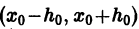
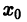
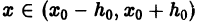
Проинтегрируем это тождество по х
Отсюда учитывая (3), получаем
так что решение у(х) задачи Коши удовлетворяет интефальному уравнению
Обратно: если непрерывная функция 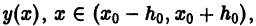
Решение 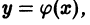
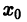
причем в качестве 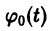
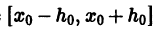
Пример:
Методом последовательных приближений решить задачу Коши
Сводим данную задачу к интегральному уравнению
Выбирая за нулевое приближение функцию
Легко видеть, что функция 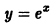
Видео:Линейное дифференциальное уравнение первого порядка (1-x^2)*y'-xy=1Скачать

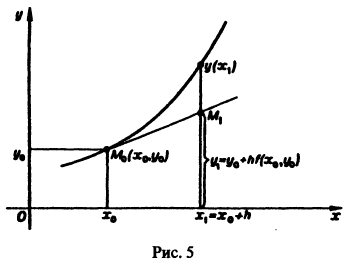
Численные методы решения задачи Коши Метод Эйлера
Пусть требуется найти приближенное решение дифференциального уравнения
удовлетворяющее начальному условию
Будем предполагать, что в некотором прямоугольнике 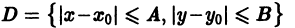
Численное решение задачи (1)-(2) состоит в построении таблицы приближенных значений 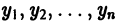
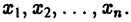
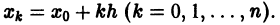
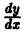
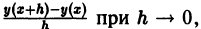
Отсюда последовательно находим значения 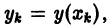
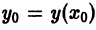
В результате вместо решения у = у(х) мы находим функцию
дискретного аргумента 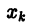
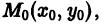
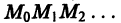
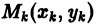
Метод Эйлера относится к группе одно-шаговых методов, в которых для вычисления точки 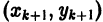
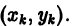
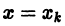
Сравнение формул (4) и (5) показывает, что они совпадают до членов первого порядка по h включительно, а погрешность формулы (4) равна 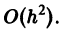
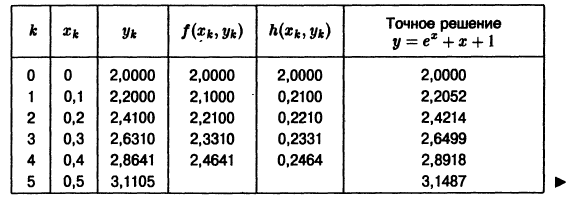
Пример:
Методом Эйлера решить задачу Коши
на отрезке |0; 0,5] с шагом h = 0,1.
В данном случае 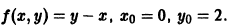
и т. д. Результаты вычислений сведем в таблицу
Замечание:
Если рассмотреть задачу Коши
на любом отрезке [0, a] с любым шагом h > 0, то получим 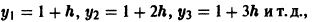
Видео:Поле направлений дифференциального уравнения первого порядкаСкачать

Понятие о методе Рунге—Кутта
Метод Эйлера весьма прост, но имеет низкую точность. Точность решения можно повысить путем усложнения разностной схемы. Весьма распространенными на практике являются схемы Рунге—Кутта.
Пусть опять требуется решить задачу Коши (1)-(2). Будем строить таблицу приближенных значений 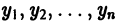
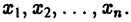
Рассмотрим схему равноотстоящих узлов 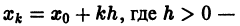
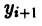
Видео:Лекция 1.4 Методы интегрирования уравнений первого порядка. Диффуры – И.В. АсташоваСкачать

Некоторые виды уравнений, интегрируемых в квадратурах
В общем случае, даже зная, что решение уравнения существует, отыскать его довольно трудно. Однако существуют некоторые виды дифференциальных уравнений, методы получения решений которых особенно просты (при помощи интегралов от элементарных функций). Рассмотрим некоторые из них.
Уравнения с разделяющимися переменными
называется дифференциальным уравнением с разделенными переменными. Здесь f1(y), f2(x) — известные непрерывные функции своих аргументов.
Покажем, как найти решение этого уравнения. Пусть 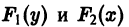
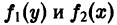
Отсюда следует, что
где С — произвольная постоянная.
Разрешая последнее уравнение (2) относительно у, получим функцию (может быть, и не одну)
которая обращает уравнение (1) в тождество и значит, является его решением.
— уравнение с разделенными переменными. Записав его в виде
и интегрируя обе части, найдем общий интеграл данного уравнения:
в котором коэффициенты при дифференциалах распадаются на множители, зависящие только от x и только от у, называется дифференциальным уравнением с разделяющимися переменными, так как путем деления на 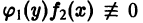
Пример:
Деля обе част уравнения на 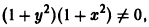
Интегрируя обе части полученного равенства, найдем
Заметим, что деление на 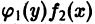
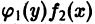
Например, разделяя переменные в уравнении
а после интегрирования —
(здесь С может принимать как положительные, так и отрицательные значения, но 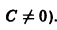
которое может быть включено в общее решение у = Сх, если постоянной С разрешить принимать значение С = 0.
Если считать переменные х и у равноправными, то уравнение
теряющее смысл при х = 0, надо дополнить уравнением
которое имеет очевидное решение х = 0.
В общем случае наряду с дифференциальным уравнением
следует рассматривать уравнение
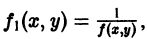
Некоторые дифференциальные уравнения путем замены переменных могут быть приведены к уравнениям с разделяющимися переменными. Например, уравнение вида
где f(x) — непрерывная функция своего аргумента, a, b, с — постоянные числа, подстановкой z = ах + by + с преобразуется в дифференциальное уравнение с разделяющимися переменными:
После интегрирования получаем
Заменяя в последнем соотношении z на ах + by + с, найдем общий интеграл уравнения (5).
Пример:
Положим z = x + y, тогда
Интегрируя, находим или
Подставляя вместо z величину х + у, получаем общее решение данного уравнения
Пример:
Известно, что скорость радиоактивного распада пропорциональна количеству х еще не распавшегося вещества. Найти зависимость х от времени t, если в начальный момент 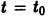
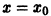
Дифференциальное уравнение процесса
Здесь к > 0 — постоянная распада — предполагается известной, знак «-» указывает на уменьшение х при возрастании t. Разделяя переменные в уравнении (») и интегрируя, получаем
Учитывая начальное условие 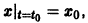
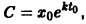
Любой процесс (не только радиоактивный распад), при котором скорость распада пропорциональна количеству еще не прореагировавшего вещества, описывается уравнением (*). Уравнение
отличающееся лишь знаком правой части от уравнения (*), описывает лавинообразный процесс размножения, например «размножение» нейтронов в цепных ядерных реакциях или размножение бактерий в предположении, что скорость их размножения пропорциональна наличному числу бактерий. Решение уравнения (»»»), удовлетворяющее условию 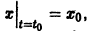
и в отличие от решения уравнения (**) возрастает с возрастанием t. Уравнения (*) и (***) можно объединить в одно
которое дает простейшую математическую модель динамики популяций (совокупности особей того или иного вида растительных или животных Организмов). Пусть y(t) — число членов популяции в момент времени t. Если предположить, что скорость изменения популяции пропорциональна величине популяции, то мы приходим к уравнению (****). Положим k=m-n, где m — коэффициент относительной скорости рождаемости, a n — коэффициент относительной скорости умирания. Тогда к > 0 при m > n и k
при к 
Уравнение динамики популяции в этой модели имеет вид
Это так называемое логистическое уравнение — фундаментальное уравнение в демографии и в математической теории экологии. Оно применяется в математической теории распространения слухов, болезней и других проблемах физиологии и социологии. Разделяя переменные в последнем уравнении, получаем
и выражая у через t, окончательно получаем
Считая, что 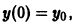
При а > 0 и А > 0 получаем, что 
Уравнения, однородные относительно x и у
Функция f(x, у) называется однородной функцией n-го измерения относительно переменных х и у, если при любом допустимом t справедливо тождество
Например, для функции
так что 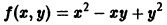
так что 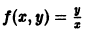
называется однородным относительно х и у, если функция f(x, у) есть однородная функция нулевого измерения относительно переменных х и у.
Пусть имеем дифференциальное уравнение
однородное относительно переменных х и у. Положив 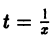
т. е. однородная функция нулевого измерения зависит только от отношения аргументов. Обозначая 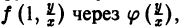
При произвольной непрерывной функции 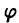
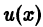
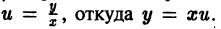
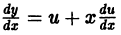
Деля обе части последнего равенства на 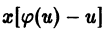
Заменяя здесь и на его значение 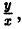
Пример:
Положим 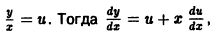
Интегрируя, найдем 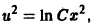
Пример:
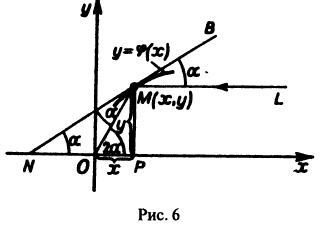
Найти форму зеркала, собирающего пучок параллельно падающих на него лучей в одну точку.
Прежде всего, зеркало должно иметь форму поверхности вращения, так как только для поверхности вращения все нормали к поверхности проходят через ось вращения.
Выберем прямоугольную декартову систему координат так, чтобы лучи были параллельны оси Ох и чтобы точкой, в которой собирались бы отраженные лучи, явилось бы начало координат. Найдем форму сечения зеркала плоскостью хОу. Пусть уравнение сечения есть 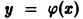
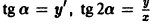
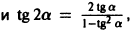
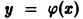
— дифференциальное уравнение, определяющее требуемый ход луча. Разрешая это уравнение относительно производной, получаем два однородных уравнения:
Первое из них путем замены 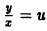
Потенцируя последнее соотношение и заменяя и через 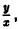
Полученное уравнение в плоскости хОу определяет семейство парабол, симметричных относительно оси Ох. фокусы всех этих парабол совпадают с началом координат. Фиксируя С и вращая параболу вокруг оси Ох, получаем параболоид вращения
Таким образом, зеркало в виде параболоида вращения решает поставленную задачу. Это свойство используется в прожекторах.
Замечание:
то уравнение (6) имеет вид
и интегрируется разделением переменных. Его общее решение
Если 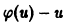
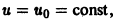
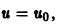
(прямая, проходящая через начало координат).
Рассмотрим уравнения, приводящиеся к однородным. Уравнение
где 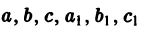
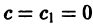
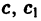
- Определитель
отличен от нуля. Введем новые переменные
по формулам
где h и k — пока не определенные постоянные. Тогда 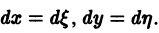
Если выбрать h и k как решения системы линейных алгебраических уравнений
то получим однородное относительно 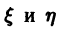
Заменяя в его общем интеграле 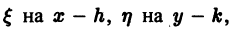
2. Определитель 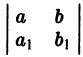
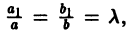
и приводится к уравнению с разделяющимися переменными подстановкой z = ax+by. Аналогичными приемами интегрируется уравнение
где f(w) — непрерывная функция своего аргумента.
Видео:4.1 Метод интегрирования по частям. Часть 1Скачать

Линейные дифференциальные уравнения
Линейным дифференциальным уравнением первого порядка называется уравнение, линейное относительно неизвестной функции и ее производной. В общем случае оно имеет вид
где коэффициенты уравнения А(х) и В(х) и его правая часть f(x) считаются известными функциями, заданными на некотором интервале
Если 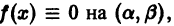
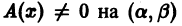
Теорема:
Если функции р(х) и q(x) непрерывны на отрезке 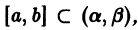
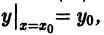
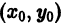
Разрешая уравнение (10) относительно у’, приведем его к виду
где правая часть
удовлетворяет всем условиям теоремы 1: она непрерывна по совокупности переменных х и у и имеет ограниченную частную производную
в указанной полосе. Отсюда следует справедливость утверждения.
Линейное однородное уравнение, соответствующее уравнению (10), имеет вид
Оно интегрируется разделением переменных:
При делении на у потеряно решение 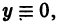
Для интегрирования неоднородного линейного уравнения
может быть применен так называемый метод вариации постоянной. Он основан на том, что общее решение уравнения (10) равно сумме общего решения уравнения (11) и какого-либо частного решения уравнения (10)
Подставляя в левую часть (11) вместо у сумму 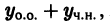
С другой стороны, разность двух частных решений 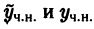
Поэтому сначала интегрируем соответствующее однородное уравнение
общее решение которого имеет вид
где С — произвольная постоянная. Решение неоднородного уравнения (10) ищем в виде
где С(х) — новая неизвестная функция.
Вычисляя производную 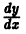
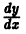
где С — новая произвольная постоянная интегрирования. Следовательно,
Это есть общее решение линейного неоднородного дифференциального уравнения (10).
В формуле (14) общего решения неопределенные интегралы можно заменить определенными интегралами с переменным верхним пределом:
Здесь 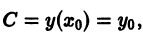
где роль произвольной постоянной играет начальное значение 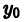
Формула (15) является общим решением уравнения (10) в форме Коши. Отсюда следует, что если р(х) и q(х) определены и непрерывны в интервале 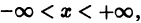
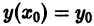
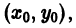
Пример:
соответствующее данному, проинтегрируем, разделяя переменные:
Решение исходного уравнения будем искать в виде
где С(х) — неизвестная функция. Находя 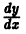
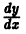
где С — постоянная интегрирования. Из формулы (**) находим общее решение уравнения (*)
Частное решение 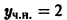
Пример:
Рассмотрим дифференциальное уравнение, описывающее изменение силы тока при замыкании цепи постоянного электрического тока.
Если R — сопротивление цепи, Е — внешняя ЭДС, то сила тока I = I(t) постепенно возрастает от значения, равного нулю, до конечного стационарного значения
Пусть L — коэффициент самоиндукции цепи, роль которой такова, что при всяком изменении силы тока в цепи появляется электродвижущая сила, равная 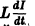
Уравнение (*) есть линейное неоднородное уравнение относительно I(t). Нетрудно видеть, что его частным решением является функция
Общее решение соответствующего однородного уравнения
откуда общее решение неоднородного уравнения (*):
При t = 0 имеем I(0) = 0, поэтому 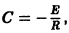
Отсюда видно, что сила тока при включении асимптотически приближается при 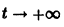
Линейное неоднородное дифференциальное уравнение
может быть проинтегрировано также следующим приемом. Будем искать решение у(х) уравнения (10) в виде
где 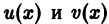
Выберем в качестве v(x) любое частное решение 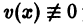
Тогда в силу (17) для u(х) получим уравнение
которое без труда интегрируется в квадратурах. Зная 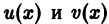
Пример:
Найти общее решение уравнения
Будем искать решение у(х) данного линейного неоднородного уравнения в виде
Подставляя 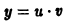
Определим функцию v(x) как решение уравнения
Разделяя переменные, найдем
Выберем любое частное решение, например, отвечающее С = 1. Тогда из (17′) получим
откуда
Для общего решения исходного уравнения получаем выражение
Преимущество метода вариации постоянной заключается в том, что он переносится на линейные неоднородные дифференциальные уравнения высшего порядка.
Уравнение Бернулли
Некоторые дифференциальные уравнения путем замены переменных могут быть сведены к линейным. К числу таких уравнений относится уравнение Бернулли
Уравнение это предложено Я. Бернулли в 1695 г., метод решения опубликовал И. Бернулли в 1697 г.
При а = 1 получаем однородное линейное уравнение
При а = 0 — неоднородное линейное уравнение
Поэтому будем предполагать, что 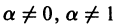
Подстановкой 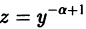
Однако уравнение Бернулли можно проинтегрировать сразу методом вариации постоянной. Это делается так. Сначала интегрируем уравнение
Его общее решение
Решение уравнения Бернулли будем искать в виде
где С(х) — новая неизвестная функция. Подставляя это выражение для у(х) в уравнение Бернулли, получаем
— уравнение с разделяющимися переменными относительно С(х). Интегрируя это уравнение,находим
где С — постоянная интегрирования. Тогда из формулы (*) получаем общий интеграл уравнения Бернулли
Замечание:
При а > 0 уравнение Бернулли имеет очевидное решение
Для интегрирования уравнения Бернулли
можно также воспользоваться подстановкой
где в качестве v(x) берется любое нетривиальное решение уравнения
а функция u(х) определяется как решение уравнения
Пример:
Найти решение уравнения Бернулли
Ищем решение у(х) уравнения в виде
Подставляя 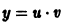
Выберем в качестве v(x) какое-нибудь ненулевое решение уравнения
и проинтегрируем его,
Поскольку нас интересует какое угодно частное решение, положим С = 1, т.е. возьмем 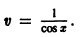
интегрируя которое, найдем
Общее решение у(х) исходного уравнения определится формулой
Уравнения в полных дифференциалах
называется уравнением в полных дифференциалах, если левая часть уравнения представляет собой полный дифференциал некоторой функции u(х, у) двух независимых переменных х и у, т. е.
В этом случае u(х, у) = С будет общим интегралом дифференциального уравнения (18).
Будем предполагать, что функции М(х, у) и N(x, у) имеют непрерывные частные производные соответственно по у и по x в некоторой односвязной области D на плоскости хОу.
Теорема:
Для того чтобы левая часть М(х, у) dx + N(x, у) dy уравнения (18) была полным дифференциалом некоторой функции и(х, у) двух независимых переменных х и у, необходимо и достаточно, чтобы выполнялось тождество
Необходимость:
Предположим, что левая часть уравнения (18) есть полный дифференциал некоторой функции u(х, у), т. е.
тогда 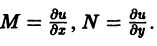
Отсюда, в силу равенства смешанных производных, вытекает тождество
Необходимость (19) доказана.
Достаточность:
Покажем, что условие (19) является и достаточным, а именно, предполагая его выполненным, найдем функцию u(х, у) такую, что du = M(x, у) dx + N(x, у) dy, или, что то же,
Найдем сначала функцию u(х, у), удовлетворяющую первому условию (20). Интегрируя это равенство по х (считаем у постоянной), получаем
где 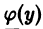
Подберем 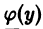
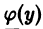
Приравняв правую часть полученного равенства к N(x, у), найдем
Левая часть последнего равенства не зависит от x. Убедимся в том, что при условии (20) в его правую часть также не входит х. Для этого покажем, что частная производная по x от правой части (22) тождественно равна нулю. Имеем
Теперь, интегрируя равенство (22) по у, получим, что
где С — постоянная интегрирования. Подставляя найденное значение для 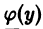
полный дифференциал которой, как нетрудно проверить, равен
Приведенный прием построения функции u(х, у) составляет метод интегрирования уравнения (18), левая часть которого есть полный дифференциал.
Пример:
Проверить, что уравнение
является уравнением в полных дифференциалах, и проинтегрировать его.
В данном случае
Следовательно, уравнение (*) есть уравнение в полных дифференциалах. Теперь находим и (см. (21)):
Находя 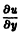
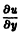
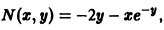
откуда 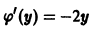
Подставив найденное выражение для 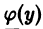
— общий интеграл исходного уравнения.
Иногда можно найти такую функцию 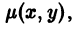
будет полным дифференциалом, хотя М dx + N dy может им и не быть. Такую функцию 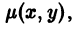
при определенных условиях на функции М(х, y) и N(x, у) интегрирующий множитель всегда существует, но отыскание его из условия
в общем случае сводится к интегрированию уравнения в частных производных, что составляет, как правило, задачу еще более трудную.
Задача:
Найти интегрирующий множитель для линейного дифференциального уравнения
Указание. Искать множитель в виде
Уравнение Риккати
где q(x), р(х), г(х) — известные функции, называется уравнением Риккати. Если р, q, г — постоянные, то оно интегрируется разделением переменных:
В случае, когда 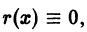
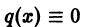
Укажем некоторые свойства уравнения Риккати.
Теорема:
Если известно одно частное решение уравнения Риккати, то его общее решение может быть получено с помощью квадратур.
Пусть известно частное решение 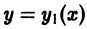
Полагая 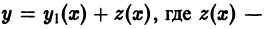
— уравнение Бернулли, которое интегрируется в квадратурах.
Пример:
Проинтегрировать уравнение Риккати
если известно его частное решение
для функции z(x) получаем
решением исходного уравнения будет функция
Частным случаем уравнения (1) является специальное уравнение Риккати:
где a, b, а — постоянные. При а = 0 имеем
и уравнение интегрируется разделением переменных.
При а = -2 получаем
Полагая 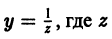
Это уравнение однородное относительно х, z. Оно интегрируется в квадратурах.
Кроме а = 0 и а = -2 существует еще бесконечное множество других значений а, при которых уравнение Риккати (3) интегрируется в квадратурах. Они задаются формулой
При всех других значениях а решение уравнения Риккати (3) не выражается в квадратурах.
Замечание. Если же положить в уравнении (3)
где u = u(x) — новая неизвестная функция, то придем к уравнению второго порядка
решение которого может быть выражено в функциях Бесселя.
Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Дифференциальные уравнения, не разрешенные относительно производной
Рассмотрим теперь общий случай уравнения первого порядка
не разрешенного относительно производной.
Уравнения, относящиеся к этому классу, весьма разнообразны, и поэтому в общем случае становится невозможным делать выводы о существовании и единственности решения, даже накладывая достаточно сильные ограничения на участвующие в уравнении функции (ограниченность, гладкость, монотонность и т. п.). Например, уравнение
вообще не имеет действительных решений. Для уравнения
решения суть прямые 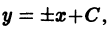
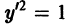
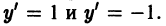
удается разрешить относительно производной у’, то получаются уравнения вида
которые иногда могут быть проинтегрированы изложенными выше методами.
Введем понятие общего решения (интеграла) для уравнения (1). Допустим, что это уравнение в окрестности точки 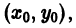
и пусть каждое из этих уравнений имеет общее решение
или общий интеграл
Совокупность общих решений (2) (или общих интегралов (3)) будем называть общим решением (общим интегралом) уравнения (1). Так, уравнение
распадается на два:
Их общие решения у = х + С, у = -х + С в совокупности составляют общее решение исходного уравнения 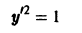
Однако не всегда уравнение (1) легко разрешимо относительно у’ и еще реже полученные после этого уравнения 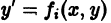
Пусть уравнение (1) имеет вид
причем существует по крайней мере один действительный корень 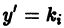
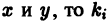
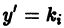
Но 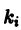
— интеграл рассматриваемого уравнения.
2. Пусть уравнение (1) имеет вид
Если это уравнение трудно разрешить относительно у’, то бывает целесообразно ввести параметр t и заменить уравнение (5) двумя:
Следовательно, искомые интегральные кривые определяются уравнениями в параметрической форме
Пример:
Полагаем,
и параметрические уравнения искомых интегральных кривых:
Если уравнение (5) легко разрешимо относительно у, то обычно за параметр берут у’. Действительно, если 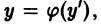
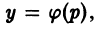
Параметрические уравнения интефальных кривых:
Исключая параметр р, получаем общий интеграл
Пример:
Разрешим уравнение относительно у:
Положим у’ = р, тогда
Таким образом, находим параметрические уравнения интегральных кривых
Параметр р здесь легко исключить. В самом деле, из первого уравнения системы находим
Первую часть второго уравнения преобразуем следующим образом:
— общее решение данного дифференциального уравнения.
3. Пусть уравнение (1) имеет вид
Если это уравнение трудно разрешить относительно у’, то, как и в предыдущем случае, целесообразно ввести параметр t и заменить уравнение (6) двумя:
Следовательно, интегральные кривые уравнения (6) определяются в параметрической форме уравнениями
Если уравнение (6) легко разрешимо относительно х:
то в качестве параметра удобно выбрать 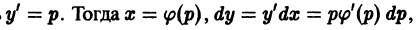
Пример:
Положим у’ = р. Тогда
В параметрической форме семейство интегральных кривых данного уравнения определяют уравнения
Уравнение Лагранжа
Уравнением Лагранжа называется дифференциальное уравнение вида
линейное относительно х и у. Здесь 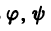
Введя параметр 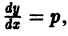
— соотношение, связывающее переменные х, у и параметр р. Чтобы получить второе соотношение, нужное для определения х и у как функций параметра р, продифференцируем (8) по х:
Уравнение (10) линейно относительно х и 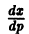
уравнения (10) и присоединив к нему уравнение
получим параметрические уравнения искомых интегральных кривых.
При переходе от уравнения (9) к (10) пришлось делить на 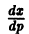
Считая р постоянным, замечаем, что уравнение (9) удовлетворяется лишь в том случае, если р является корнем уравнения
Итак, если уравнение 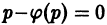
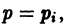
— это прямые линии.
Уравнение Клеро
Уравнением Клеро называется дифференциальное уравнение вида
Полагая у’ = р, получаем
Дифференцируя по х, имеем
откуда или 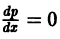
В первом случае, исключая р, найдем семейство прямых
— общее решение уравнения Клеро. Оно находится без квадратур и представляет собой однопараметрическое семейство прямых. Во втором случае решение определяется уравнениями
Можно показать, что, как правило, интегральная кривая (12) является огибающей найденного семейства прямых.
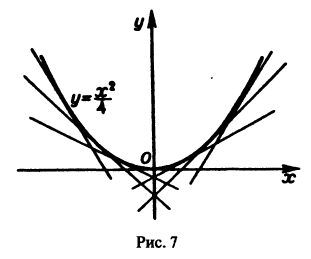
Пример:
Решить уравнение Клеро
Общее решение данного уравнения видно сразу:
Другое (особое) решение определяется уравнениями
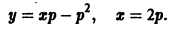
Исключая параметр р, находим
— огибающую прямых
Для уравнения вида
через некоторую точку 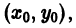
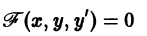
и если каждое из уравнений 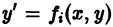
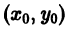
Поэтому свойство единственности решения уравнения 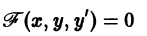
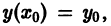
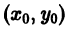
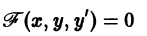
Например, для решений уравнения
свойство единственности в этом смысле всюду выполнено, поскольку через каждую точку 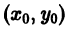
(см. пример 4) через точку (0,0) проходят также две интегральные линии: прямая
входящая в общее решение этого уравнения, и парабола
причем эти линии имеют в точке (0,0) одно и то же направление:
Таким образом, в точке (0,0) свойство единственности нарушается.
Теорема:
Пусть имеем уравнение
и пусть в некоторой окрестности точки 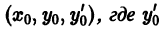
функция 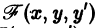
1) 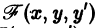
2) производная 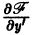
3) существует ограниченная производная
Тогда найдется отрезок 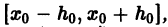
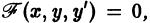
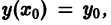
Геометрические вопросы, связанные с дифференциальными уравнениями 1-го порядка. Ортогональные траектории
Общее решение 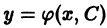
Поставим теперь в некотором смысле обратную задачу: дано однопараметрическое семейство кривых
и требуется составить дифференциальное уравнение, для которого 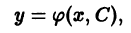
Итак, пусть дано соотношение
где С — параметр. Дифференцируя (1) по х, получим
Если правая часть (2) уже не содержит С, то формула (2) будет представлять дифференциальное уравнение семейства кривых (1). Например, если 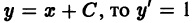
Пусть теперь правая часть (2) содержит С. Разрешая соотношение (1) относительно С, определим С как функцию х и у:
Подставляя это выражение для С в формулу (2), получим дифференциальное уравнение 1-го порядка
Нетрудно убедиться в том, что 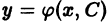
Если соотношение между величинами х, у и С задано в виде
то, дифференцируя его по х, получим
Исключая С из соотношений (5) и (6), приходим к уравнению
Можно показать, что (5) является общим интегралом уравнения (7).
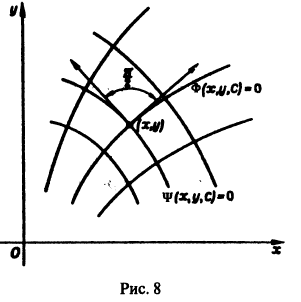
Ортогональные траектории
В ряде прикладных вопросов встречается следующая задача. Дано семейство кривых
Требуется найти такое семейство
чтобы каждая кривая семейства Ф(х, у, С) = 0, проходящая через точку (х, у), пересекалась в этой точке кривой семейства 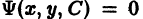
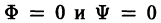
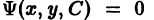
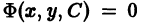
Аналитически это означает следующее. Если
есть дифференциальное уравнение семейства
то дифференциальное уравнение траекторий, ортогональных к семейству Ф = 0, имеет вид
(угловые коэффициенты касательных к кривым семейств 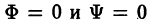
Таким образом, чтобы найти ортогональные траектории к семейству 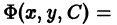
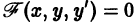
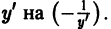
Пример:
Найти ортогональные траектории семейства
окружностей с центром в начале координат.
Составляем дифференциальное уравнение семейства (8). Дифференцируя (8) по х, получим
Это дифференциальное уравнение данного семейства. Заменив в нем 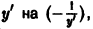
Интегрируя последнее уравнение, получаем, что искомыми ортогональными траекториями будут полупрямые (рис. 9)
Видео:9. Метод вариации произвольной постоянной ( метод Лагранжа ). Линейные дифференциальные уравнения.Скачать

Дополнение к дифференциальным уравнениям первого порядка










Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
💡 Видео
Математика без Ху!ни. Метод неопределенных коэффициентов.Скачать

18+ Математика без Ху!ни. Дифференциальные уравнения. Однородное уравнение.Скачать

2. Дифференциальные уравнения с разделяющимися переменными. Часть 1.Скачать

Методы интегрирования. 11 класс.Скачать

Метод ЭйлераСкачать








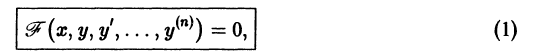

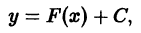
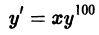
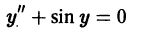
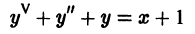
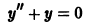
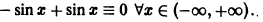
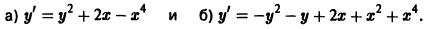
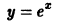
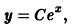
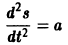
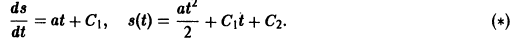
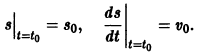

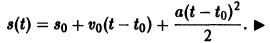



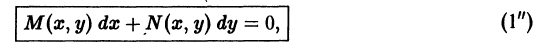
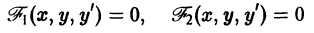
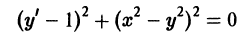
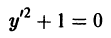
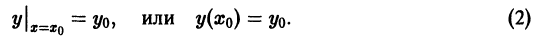

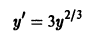
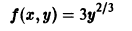
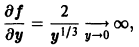
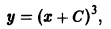
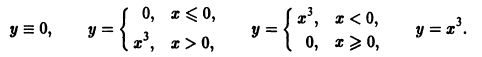
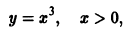
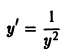
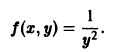
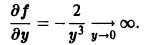
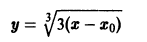
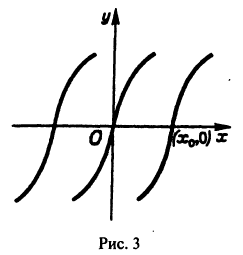
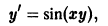
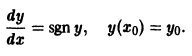

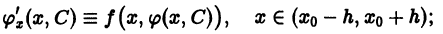
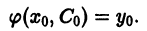
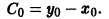
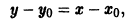

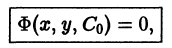
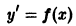
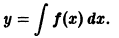
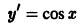
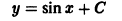
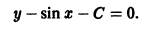
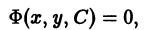

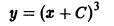
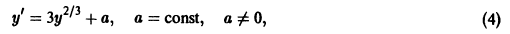
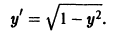

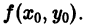
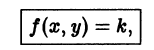
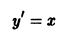
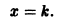
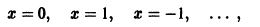
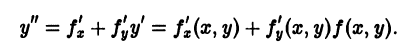
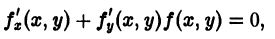
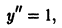


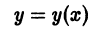
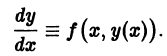
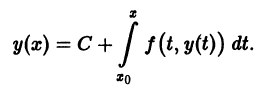
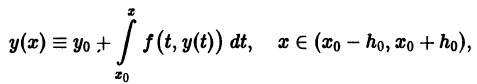
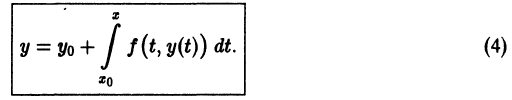
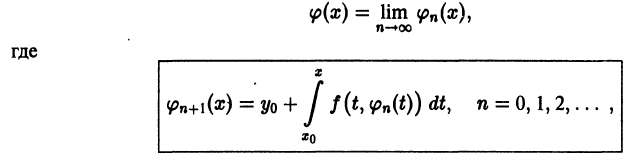
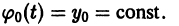
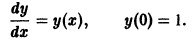
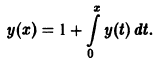
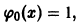
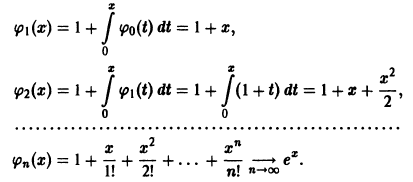


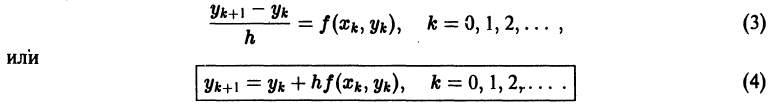
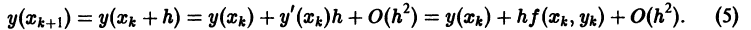
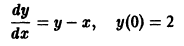
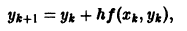
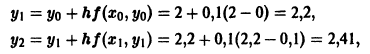
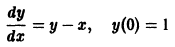
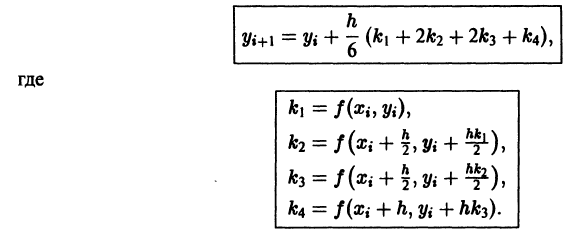

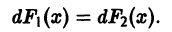

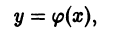
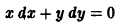
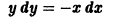
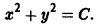
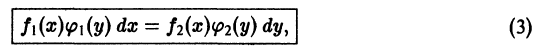
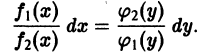
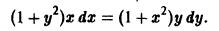
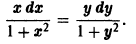


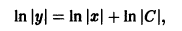
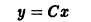
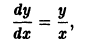
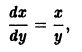



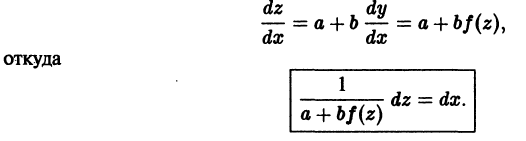
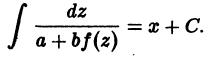
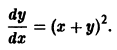
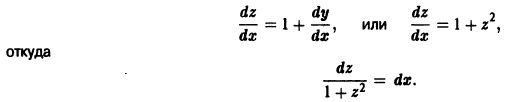

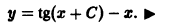

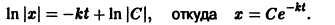


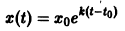

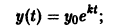
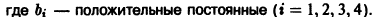
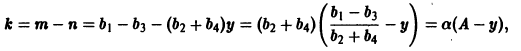
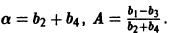
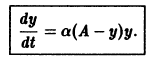

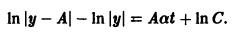
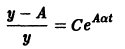
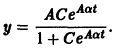
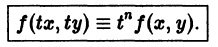
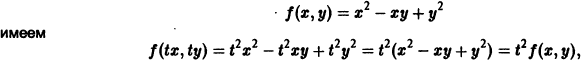
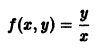
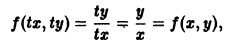
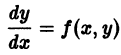
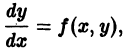
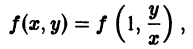

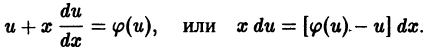
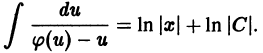
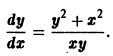
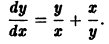

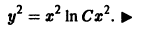
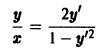
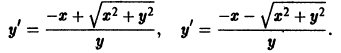
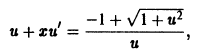
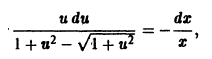
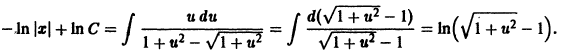

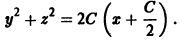
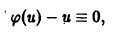
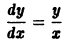
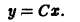
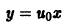

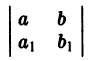 отличен от нуля. Введем новые переменные
отличен от нуля. Введем новые переменные