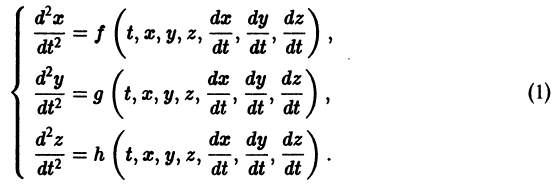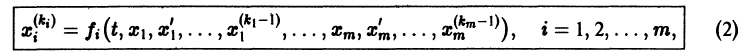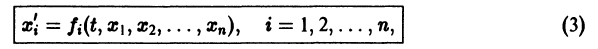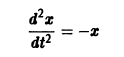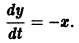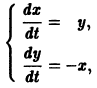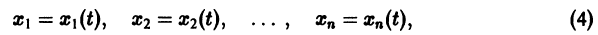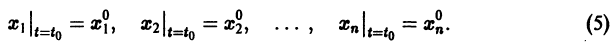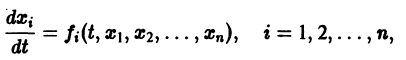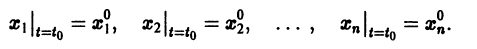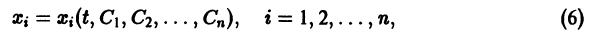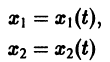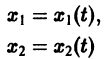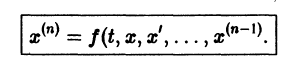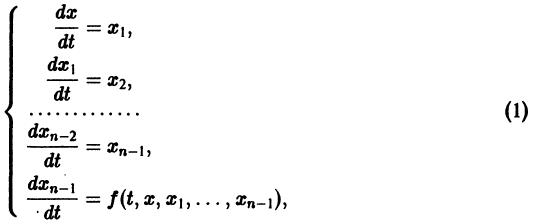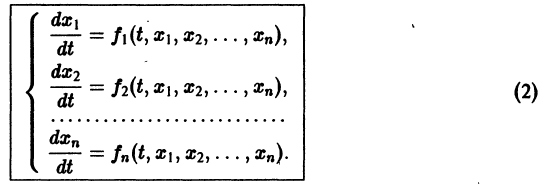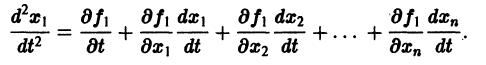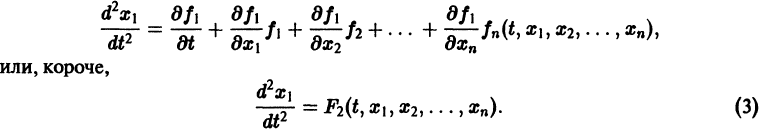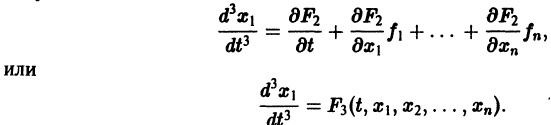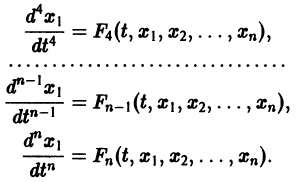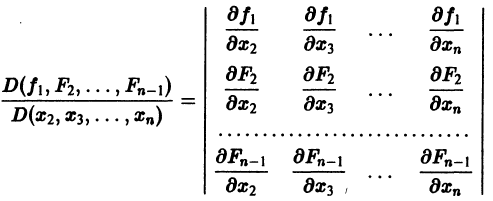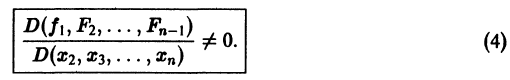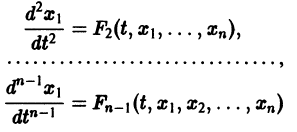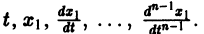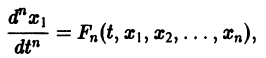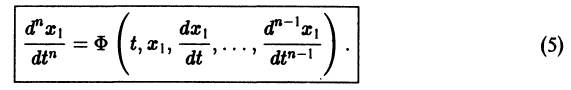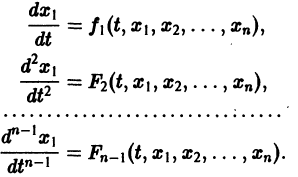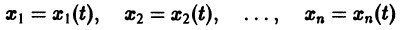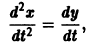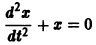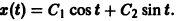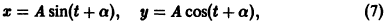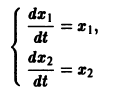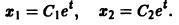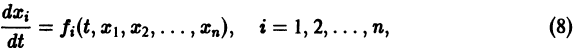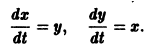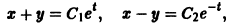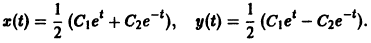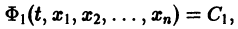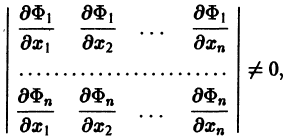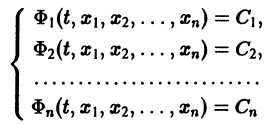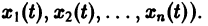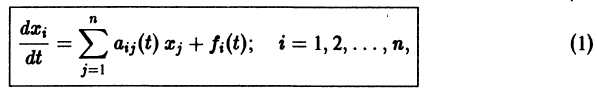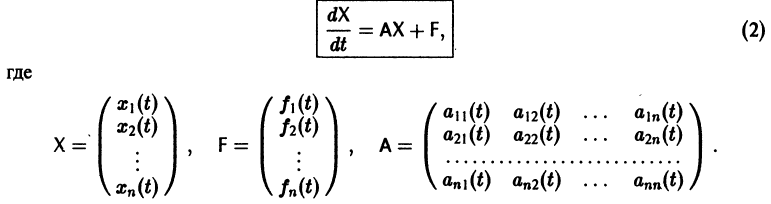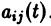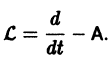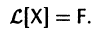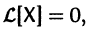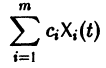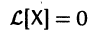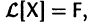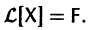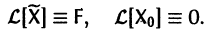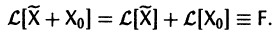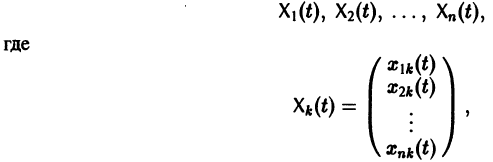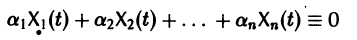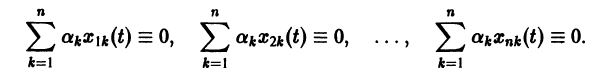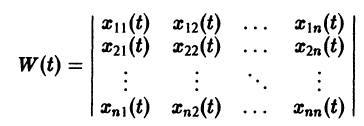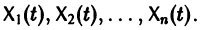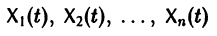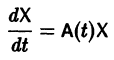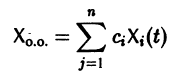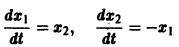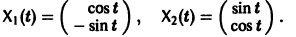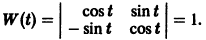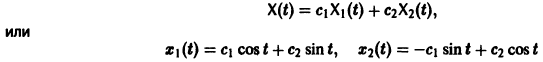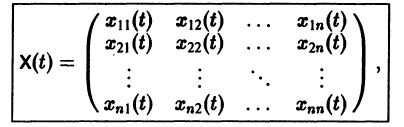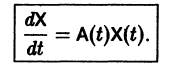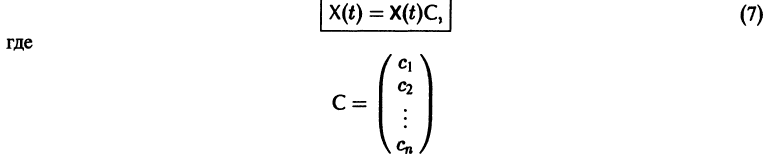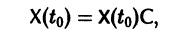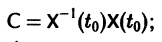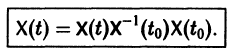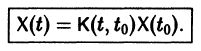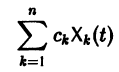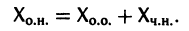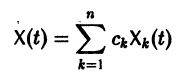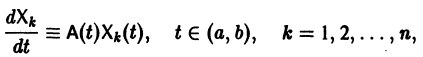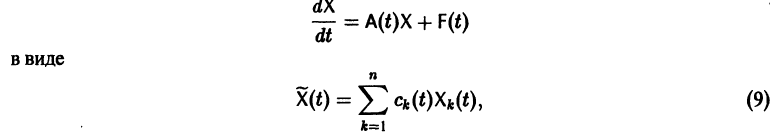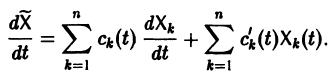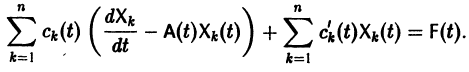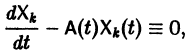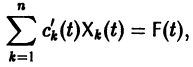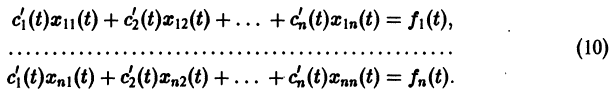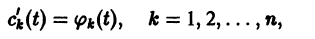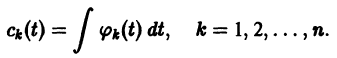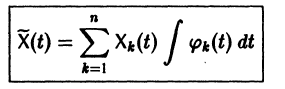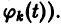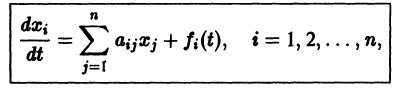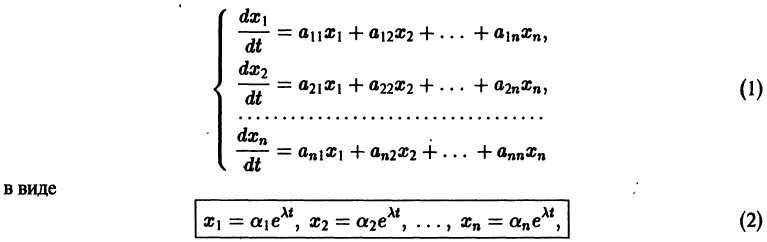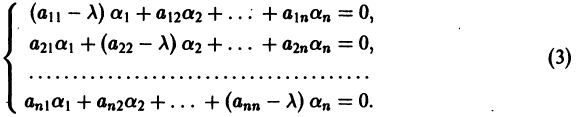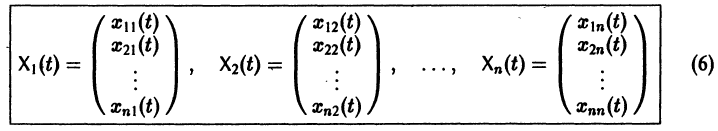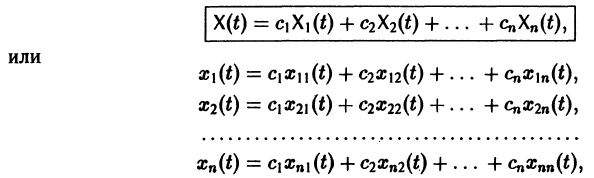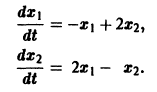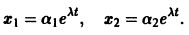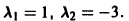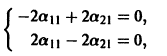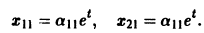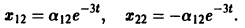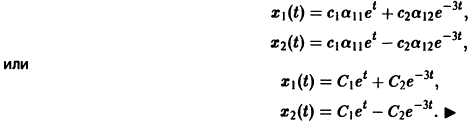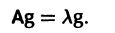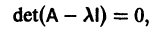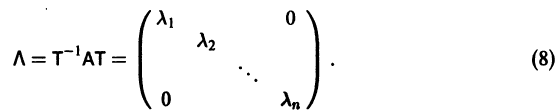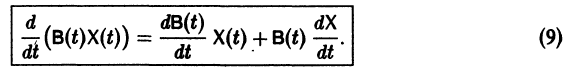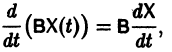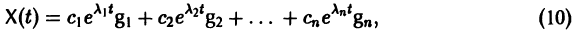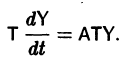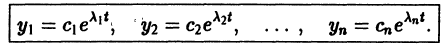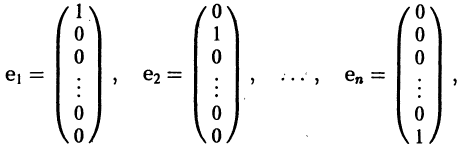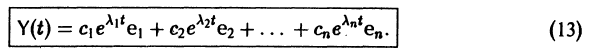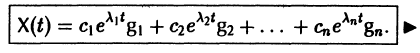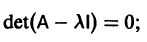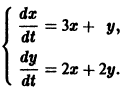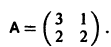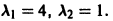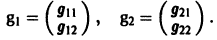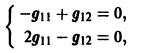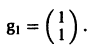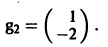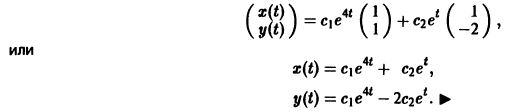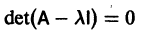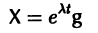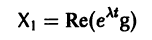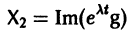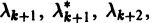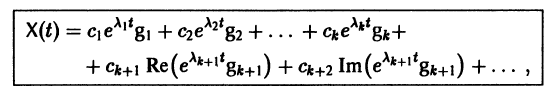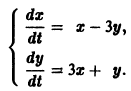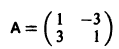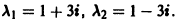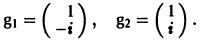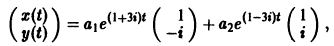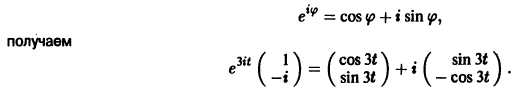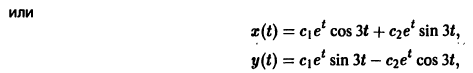Рассмотрим систему дифференциальных уравнений
- МЕТОД ПОСЛЕДОВАТЕЛЬНОГО ИНТЕГРИРОВАНИЯ
- МЕТОД ИСКЛЮЧЕНИЯ
- Системы дифференциальных уравнений с примерами решения и образцами выполнения
- Решение систем дифференциальных уравнений
- Методы интегрирования систем дифференциальных уравнений
- Метод исключения
- Метод интегрируемых комбинаций
- Системы линейных дифференциальных уравнений
- Фундаментальная матрица
- Квадратная матрица
- Метод вариации постоянных
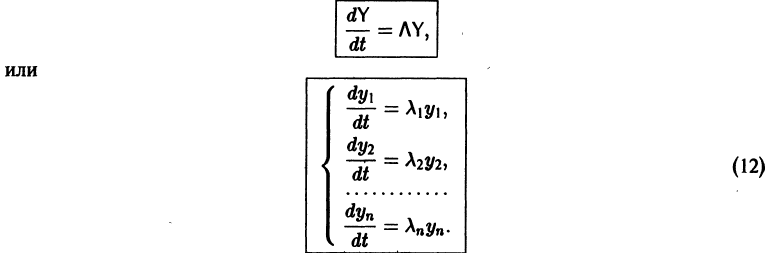
- Системы линейных дифференциальных уравнений с постоянными коэффициентами
- Метод Эйлера
- Матричный метод
- Понятие о системах дифференциальных уравнений
- Виды дифференциальных уравнений
- Дифференциальные уравнения первого порядка
- Простейшие дифференциальные уравнения первого порядка вида y ‘ = f ( x )
- Дифференциальные уравнения с разделяющимися переменными вида f 1 ( y ) · g 1 ( x ) d y = f 2 ( y ) · g 2 ( x ) d x или f 1 ( y ) · g 1 ( x ) · y ‘ = f 2 ( y ) · g 2 ( x )
- Линейные неоднородные дифференциальные уравнения первого порядка y ‘ + P ( x ) · y = Q ( x )
- Дифференциальное уравнение Бернулли y ‘ + P ( x ) y = Q ( x ) y a
- Уравнения в полных дифференциалах P ( x , y ) d x + Q ( x , y ) d y = 0
- Дифференциальные уравнения второго порядка
- Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами y ‘ ‘ + p y ‘ + q y = 0 , p , q ∈ R
- Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами y ‘ ‘ + p y ‘ + q y = f ( x ) , p , q ∈ R
- Линейные однородные дифференциальные уравнения (ЛОДУ) y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = 0 и линейные неоднородные дифференциальные уравнения (ЛНДУ) второго порядка y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = f ( x )
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения, допускающие понижение порядка
- Линейные однородные и неоднородные дифференциальные уравнения высших порядков с постоянными коэффициентами y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = 0 и y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = f ( x )
- Линейные однородные и неоднородные дифференциальные уравнения высших порядков y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 1 ( x ) · y ‘ + f 0 ( x ) · y = 0 и y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 1 ( x ) · y ‘ + f 0 ( x ) · y = f ( x )
- Системы дифференциальных уравнений вида d x d t = a 1 x + b 1 y + c 1 d y d t = a 2 x + b 2 y + c 2
- 🔍 Видео
Видео:Видеоурок "Системы дифференциальных уравнений"Скачать

МЕТОД ПОСЛЕДОВАТЕЛЬНОГО ИНТЕГРИРОВАНИЯ
Пусть система (15) с точностью до переобозначения переменных ух, у2, г/3, . уп имеет вид
Тогда ее интегрирование, вообще говоря, можно выполнить последовательно. Действительно, в первое уравнение системы не входят другие искомые функции, кроме ух, т. е. его можно рассматривать как дифференциальное уравнение первого порядка относительно независимой переменной х и искомой функции ух. Интегрируя его, если это возможно, найдем функцию ух = (рх(л:, сх). Затем подставляем фДх, сх) вместо ух во все остальные уравнения системы. Очевидно, второе уравнение при этом примет вид
т. е. в него не будут входить другие искомые функции, кроме у2. Интегрируя его, получим функцию у2 = cp2(^c, сх, с2). Продолжая этот процесс, в силу вида системы (16) мы найдем общее решение системы (16)
Видео:Решение системы дифференциальных уравнений методом ЭйлераСкачать

МЕТОД ИСКЛЮЧЕНИЯ
Многие системы в нормальной форме удается проинтегрировать путем предварительного приведения данной системы /г-го порядка к одному дифференциальному уравнению п-го порядка относительно какой либо из функций
у, (х), например, у„(х) (или к нескольким таким уравнениям, причем сумма их порядков будет равна п). Такое приведение достигается последовательным выражением функдий y^x) (t = 1, n — 1) из некоторых уравнений системы (15) и исключением этих функций из всех других уравнений. Полученное уравнение /г-го порядка интегрируется известными методами. После этого функции у(х), у2(х), у3(х), . yn-i(x) определяются из их представления через У,X х )-
Опишем теперь более точно процесс исключения из системы уравнений всех неизвестных функций, кроме одной.
Покажем вначале, что одна из неизвестных функций, например у(х), входящая в состав решения у(х), у2(х), у3(х), . yn
i(x), уп(х) системы дифференциальных уравнений (15), удовлетворяет некоторому уравнению п-го порядка, при этом мы предположим, что все функции /, имеют непрерывные частные производные до (п — 1)-го порядка включительно по всем аргументам. Подставив в систему (15) некоторое решение г/х(х), у2<х), у3(х), . у„(х), обратим все уравнения в тождества. В частности, в тождество обратится и первое уравнение системы
Продифференцируем это тождество по х: или
и, обозначив правую часть последнего тождества F2(x, ух, . /„), получим
Снова дифференцируем это тождество или
и, обозначив правую часть последнего тождества F3(x, ylt . уп), получим:
Опять продифференцируем это тождество и, продолжая этот процесс п — 2 раза, получим, в итоге, тождество
дифференцируя которое еще раз и пользуясь тождествами (15), будем иметь:
В итоге получены п — 1 тождеств 
Предположим, что в рассматриваемой области определитель
Тогда систему (22) можно разрешить относительно у2, у3, у4, . уп, выразив их через переменные х, уи

которому удовлетворяет функция yi(x), являвшаяся по предположению функцией ух(х) решения ух(х), у2(х), у2(х), . уп(х) системы (15).
Нетрудно показать, что если взять любое решение ух(х) полученного уравнения п-го порядка (24), подставить его в систему (22) и определить из этой системы у2(х), у2(х), . уп(х), то система функций
Видео:7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

Системы дифференциальных уравнений с примерами решения и образцами выполнения
Также как и обыкновенные дифференциальные уравнения, системы дифференциальных уравнений применяются для описания многих процессов реальной действительности. В частности, к ним относятся различного рода физические и химические процессы, процессы нефте- и газодобычи, геологии, экономики и т.д. Действительно, если некоторые физические величины (перемещение тела, пластовое давление жидкости в фиксированной точке с тремя координатами, концентрация веществ, объемы продаж продуктов) оказываются меняющимися со временем под воздействием тех или иных факторов, то, как правило, закон их изменения по времени описывается именно системой дифференциальных уравнений, т.е. системой, связывающей исходные переменные как функции времени и производные этих функций. Независимой переменной в системе дифференциальных уравнений может выступать не только время, но и другие физические величины: координата, цена продукта и т.д.
Видео:Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать

Решение систем дифференциальных уравнений
К системе дифференциальных уравнений приводит уже простейшая задача динамики точки: даны силы, действующие на материальную точку; найти закон движения, т. е. найти функции 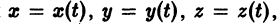
Здесь x, у, z — координаты движущейся точки, t — время, f, g, h — известные функции своих аргументов.
Система вида (1) называется канонической. Обращаясь к общему случаю системы т дифференциальных уравнений с т неизвестными функциями 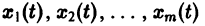
разрешенную относительно старших производных. Система уравнений первого порядка, разрешенных относительно производных от искомых функций,
Если 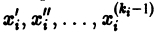
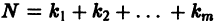
Например, одно уравнение
является мастным случаем канонической системы. Положив 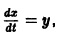
В результате получаем нормальную систему уравнений
эквивалентную исходному уравнению.
Определение:
Решением нормальной системы (3) на интервале (а, Ь) изменения аргумента t называется всякая система n функций
дифференцируемых на интервале а
Теорема:
Существования и единственности решения задачи Коши. Пусть имеем нормальную систему дифференциальных уравнений
и пусть функции 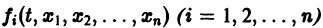
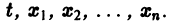

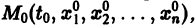

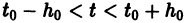
Определение:
Система n функций
зависящих от t и n произвольных постоянных 

1) при любых допустимых значениях 
2) в области 
Решения, получающиеся из общего при конкретных значениях постоянных 
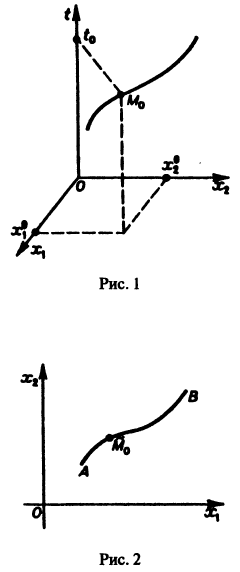
Обратимся для наглядности к нормальной системе двух уравнений,
Будем рассматривать систему значений t, x1, х2 как прямоугольные декартовы координаты точки трехмерного пространства, отнесенного к системе координат 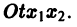
системы (7), принимающее при 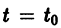
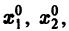
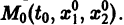
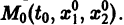
Нормальной системе (7) и ее решению можно придать еще такое истолкование: будем независимую переменную t рассматривать как параметр, а решение
системы — как параметрические уравнения кривой на плоскости 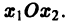
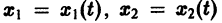
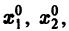
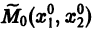
Методы интегрирования систем дифференциальных уравнений
Метод исключения
Один из методов интегрирования — метод исключения. Частным случаем канонической системы является одно уравнение n-го порядка, разрешенное относительно старшей производной
Введя новые функции 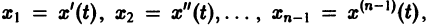
т. е. одно уравнение n-го порядка эквивалентно нормальной системе (1)
Можно утверждать и обратное, что, вообще говоря, нормальная система п уравнений первого порядка эквивалентна одному уравнению порядка n. На этом и основан метод исключения для интегрирования систем дифференциальных уравнений.
Делается это так. Пусть имеем нормальную систему
Продифференцируем первое из уравнений (2) по t. Имеем
Заменяя в правой части производные 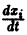
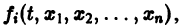
Уравнение (3) снова дифференцируем по t. Принимая во внимание систему (2), получим
Продолжая этот процесс, найдем
Предположим, что определитель
(якобиан системы функций 
Тогда система уравнений, составленная из первого уравнения системы (2) и уравнений
будет разрешима относительно неизвестных 

Внося найденные выражения в уравнение
получим одно уравнение n-го порядка
Из самого способа его построения следует, что если 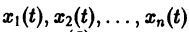
Обратно, пусть Х1(t) — решение уравнения (5). Дифференцируя это решение по t, вычислим 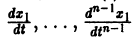
от t в систему уравнений
По предположению эту систему можно разрешить относительно 

Можно показать, что так построенная система функций
составляет решение системы дифференциальных уравнений (2). Пример:
Требуется проинтегрировать систему
Дифференцируя первое уравнение системы, имеем
откуда, используя второе уравнение, получаем
— линейное дифференциальное уравнение второго порядка с постоянными коэффициентами с одной неизвестной функцией. Его общее решение имеет вид
В силу первого уравнения системы находим функцию
Найденные функции x(t), y(t), как легко проверить, при любых значениях С1 и С2 удовлетворяют заданной системе.
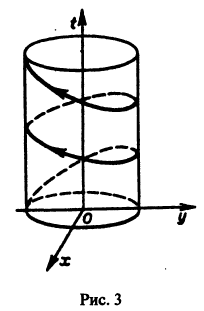
Функции x(t), y(t) можно представить в виде
откуда видно, что интегральные кривые системы (6) — винтовые линии с шагом 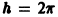
Исключая в формулах (7) параметр t, получаем уравнение
так что фазовые траектории данной системы суть окружности с центром в начале координат — проекции винтовых линий на плоскость хОу.
При А = 0 фазовая траектория состоит из одной точки х = 0, у = 0, называемой точкой покоя системы.
Замечание:
Может оказаться, что функции 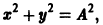
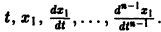
нельзя заменить эквивалентным уравнением второго порядка относительно х1 или x2. Эта система составлена из пары уравнений 1-го порядка, каждое из которых интегрируется независимо, что дает
Метод интегрируемых комбинаций
Интегрирование нормальных систем дифференциальных уравнений
иногда осуществляется методом интегрируемых комбинаций.
Интегрируемой комбинацией называется дифференциальное уравнение, являющееся следствием уравнений (8), но уже легко интегрирующееся.
Пример:
Складывая почленно данные уравнения, находим одну интегрируемую комбинацию:
Вычитая почленно из первого уравнения системы второе, получаем вторую интегрируемую комбинацию:
Мы нашли два конечных уравнения
из которых легко определяется общее решение системы:
Одна интегрируемая комбинация дает возможность получить одно уравнение
связывающее независимую переменную t и неизвестные функции 
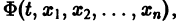
Если найдено п первых интегралов системы (8) и все они независимы, т. е. якобиан системы функций 
то задача интефирования системы (8) решена (так как из системы
определяются все неизвестные функции
Системы линейных дифференциальных уравнений
Система дифференциальных уравнений называется линейной, если она линейна относительно неизвестных функций и их производных, входящих в уравнение. Система n линейных уравнений первого порядка, записанная в нормальной форме, имеет вид
или, в матричной форме,
Теорема:
Если все функции 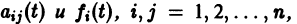
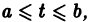
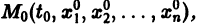
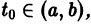
Действительно, в таком случае правые части системы (1) непрерывны по совокупности аргументов t, 
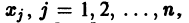
Введем линейный оператор
Тогда система (2) запишется в виде
Если матрица F — нулевая, т. е. 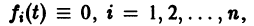
Приведем некоторые теоремы, устанавливающие свойства решений линейных систем.
Теорема:
Если X(t) является решением линейной однородной системы
то cX(t), где с — произвольная постоянная, является решением той же системы.
Теорема:
двух решений 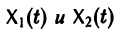
Следствие:
с произвольными постоянными коэффициентами сi решений 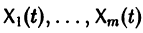
является решением той же системы.
Теорема:
Если 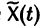
a Xo(t) — решение соответствующей однородной системы
будет решением неоднородной системы
Действительно, по условию,
Пользуясь свойством аддитивности оператора 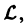
Это означает, что сумма 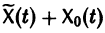
Определение:
называются линейно зависимыми на интервале a
при 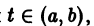

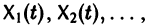
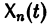
Заметим, что одно векторное тождество (5) эквивалентно n тождествам:
называется определителем Вронского системы векторов
Определение:
Пусть имеем линейную однородную систему
где 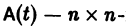
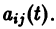
линейной однородной системы (6), линейно независимых на интервале а
с непрерывными на отрезке 
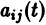
(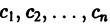
Пример:
имеет, как нетрудно проверить, решения
Эти решения линейно независимы, так как определитель Вронского отличен от нуля:
Общее решение системы имеет вид
(с1, с2 — произвольные постоянные).
Фундаментальная матрица
Квадратная матрица
столбцами которой являются линейно независимые решения 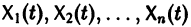
Если Х(t) — фундаментальная матрица системы (6), то общее решение системы можно представить в виде
— постоянная матрица-столбец с произвольными элементами. Полагая в (7) t = t0, имеем
Матрица 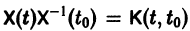
Теорема:
О структуре общего решения линейной неоднородной системы дифференциальных уравнений. Общее решение в области 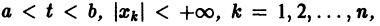
с непрерывными на отрезке 
соответствующей однородной системы и какого-нибудь частного решения 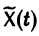
Метод вариации постоянных
Если известно общее решение линейной однородной системы (6), то частное решение неоднородной системы можно находить методом вариации постоянных (метод Лагранжа).
есть общее решение однородной системы (6), тогда
причем решения Xk(t) линейно независимы.
Будем искать частное решение неоднородной системы
где 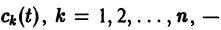
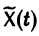
Подставляя 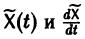
то для определения 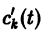
или, в развернутом виде,
Система (10) есть линейная алгебраическая система относительно 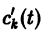
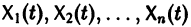
где 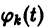
Подставляя эти значения 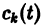
(здесь под символом 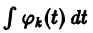
Системы линейных дифференциальных уравнений с постоянными коэффициентами
Рассмотрим линейную систему дифференциальных уравнений
в которой все коэффициенты 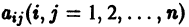
Мы рассмотрим еще метод Эйлера интегрирования линейных однородных систем дифференциальных уравнений с постоянными коэффициентами. Он состоит в следующем.
Метод Эйлера
Будем искать решение системы
где 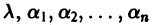
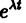
Для того, чтобы эта система (3) линейных однородных алгебраических уравнений с n неизвестными 
Уравнение (4) называется характеристическим. В его левой части стоит многочлен относительно 


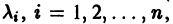
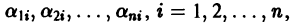
где второй индекс указывает номер решения, а первый — номер неизвестной функции. Построенные таким образом п частных решений линейной однородной системы (1)
образуют, как можно проверить, фундаментальную систему решений этой системы.
Следовательно, общее решение однородной системы дифференциальных уравнений (1) имеет вид
где 
Случай, когда характеристическое уравнение имеет кратные корни, мы рассматривать не будем.
Пример:
Ищем решение в виде
имеет корни
Система (3) для определения a1, а2 выглядит так:
Подставляя в (*) 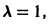
откуда а21 = а11. Следовательно,
Полагая в 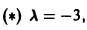
Общее решение данной системы:
Матричный метод
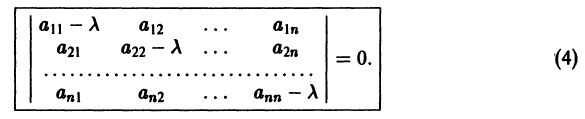
Изложим еще матричный метод интегрирования однородной системы (1). Запишем систему (1) в виде

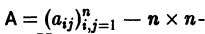
Напомним некоторые понятия из линейной алгебры. Вектор 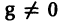
Число 
где I — единичная матрица.
Будем предполагать, что все собственные значения 
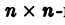
Столбцами матрицы Т являются координаты собственных векторов g1, g2 …, gn матрицы А.
Введем еще следующие понятия. Пусть В(t) — 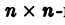








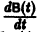
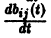
Пусть B(t) — n х n-матрица,
— вектор-столбец. Учитывая правила алгебры матриц, непосредственной проверкой убеждаемся в справедливости формулы
В частности, если В — постоянная матрица, то
так как 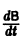
Теорема:
Если собственные значения 
где g1, g2,…, gn — собственные векторы-столбцы матрицы А, 
Введем новый неизвестный вектор-столбец Y(t) по формуле
где Т — матрица, приводящая матрицу А к диагональному виду. Подставляя X(t) из (11) в (7), получим систему
Умножая обе части последнего соотношения слева на 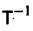
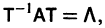
Мы получили систему из n независимых уравнений, которая без труда интегрируется:
Здесь 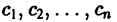
Вводя единичные n-мерные векторы-столбцы
решение Y(t) можно представить в виде
В силу (11) Х(t) = TY(t). Так как столбцы матрицы Т есть собственные векторы матрицы 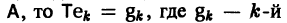
Таким образом, если матрица А системы дифференциальных уравнений (7) имеет различные собственные значения, для получения общего решения этой системы:
1) находим собственные значения 
2) находим все собственные векторы g1, g2,…, gn;
3) выписываем общее решение системы дифференциальных уравнений (7) по формуле (10).
Пример:
Матрица А системы имеет вид
1) Составляем характеристическое уравнение
Корни характеристического уравнения
2) Находим собственные векторы
Для 
откуда g11 = g12, так что
Аналогично для 
3) Пользуясь формулой (10), получаем общее решение системы дифференциальных уравнений
Корни характеристического уравнения могут быть действительными и комплексными. Так как по предположению коэффициенты 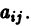
будет иметь действительные коэффициенты. Поэтому наряду с комплексным корнем 




При комплексном 
системы (7) также будет комплексным. Действительная часть
этого решения являются решениями системы (7). Собственному значению 



Пусть 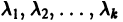
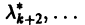
где сi — произвольные постоянные.
Пример:
1) Характеристическое уравнение системы
Его корни
2) Собственные векторы матриц
3) Решение системы
где а1, а2 — произвольные комплексные постоянные.
Найдем действительные решения системы. Пользуясь формулой Эйлера
Следовательно, всякое действительное решение системы имеет
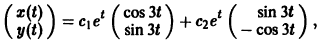
где с1, с2 — произвольные действительные числа.
Видео:Дифференциальные уравнения, 1 урок, Дифференциальные уравнения. Основные понятияСкачать

Понятие о системах дифференциальных уравнений


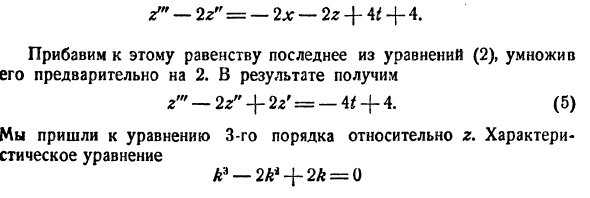

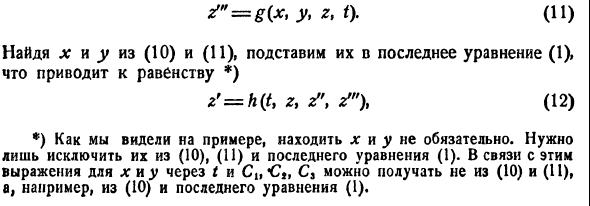

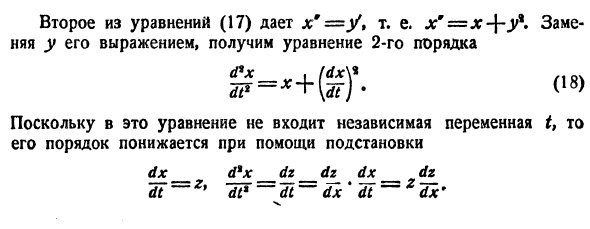

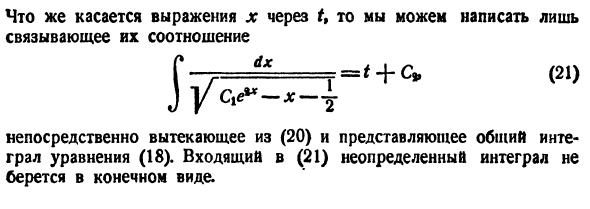

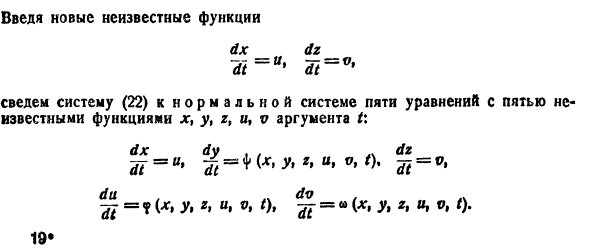
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:Поле направлений дифференциального уравнения первого порядкаСкачать

Виды дифференциальных уравнений
Существует целый ряд задач, в которых установить прямую связь между величинами, применяемыми для описания процесса, не получается. Единственное, что можно сделать, это получить равенство, запись которого включает производные исследуемых функций, и решить его. Решение дифференциального уравнения позволяет установить непосредственную связь между величинами.
В этом разделе мы займемся разбором решений дифференциальных уравнений, неизвестная функция в которых является функцией одной переменной. Мы построили теоретическую часть таким образом, чтобы даже человек с нулевым представлением о дифференциальных уравнениях мог без труда получить необходимые знания и справиться с приведенными задачами.
Если какие-то термины окажутся для вас новыми, обратитесь к разделу «Определения и понятия теории дифференциальных уравнений». А тем временем перейдем к рассмотрению вопроса о видах дифференциальных уравнений.
Для каждого из видов дифференциальных уравнений применяется свой метод решения. В этом разделе мы рассмотрим все эти методы, приведем примеры с подробными разборами решения. После ознакомления с темой вам необходимо будет определять вид дифференциального уравнения и выбирать наиболее подходящий из методов решения поставленной задачи.
Возможно, прежде чем приступить к решению дифференциальных уравнений, вам придется освежить в памяти такие темы как «Методы интегрирования» и «Неопределенные интегралы».
Начнем ознакомление с темой мы с видов обыкновенных дифференциальных уравнений 1 -го порядка. Эти уравнения могут быть разрешены относительно производной. Затем перейдем в ОДУ 2 -го и высших порядков. Также мы уделим внимание системам дифференциальных уравнений.
Напомним, что y ‘ = d x d y , если y является функцией аргумента x .
Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Дифференциальные уравнения первого порядка
Простейшие дифференциальные уравнения первого порядка вида y ‘ = f ( x )
Начнем с примеров таких уравнений.
y ‘ = 0 , y ‘ = x + e x — 1 , y ‘ = 2 x x 2 — 7 3
Оптимальным для решения дифференциальных уравнений f ( x ) · y ‘ = g ( x ) является метод деления обеих частей на f ( x ) . Решение относительно производной позволяет нам прийти к уравнению вида y ‘ = g ( x ) f ( x ) . Оно является эквивалентом исходного уравнения при f ( x ) ≠ 0 .
Приведем примеры подобных дифференциальных уравнений:
e x · y ‘ = 2 x + 1 , ( x + 2 ) · y ‘ = 1
Мы можем получить ряд дополнительных решений в тех случаях, когда существуют значения аргумента х , при которых функции f ( x ) и g ( x ) одновременно обращаются в 0 . В качестве дополнительного решения в уравнениях f ( x ) · y ‘ = g ( x ) при заданных значениях аргумента может выступать любая функция, определенная для заданного значения х .
Наличие дополнительных решений возможно для дифференциальных уравнений x · y ‘ = sin x , ( x 2 — x ) · y ‘ = ln ( 2 x 2 — 1 )
Ознакомиться с теоретической частью и примерами решения задач таких уравнений вы можете в разделе «Простейшие дифференциальные уравнения 1 -го порядка».
Дифференциальные уравнения с разделяющимися переменными вида f 1 ( y ) · g 1 ( x ) d y = f 2 ( y ) · g 2 ( x ) d x или f 1 ( y ) · g 1 ( x ) · y ‘ = f 2 ( y ) · g 2 ( x )
Поговорим теперь об уравнениях с разделенными переменными, которые имеют вид f ( y ) d y = g ( x ) d x . Как следует из названия, к данному виду дифференциальных уравнений относятся выражения, которые содержат переменные х и у , разделенные знаком равенства. Переменные находятся в разных частях уравнения, по обе стороны от знака равенства.
Решить уравнения с разделенными переменными можно путем интегрирования обеих его частей: ∫ f ( y ) d y = ∫ f ( x ) d x
К числу дифференциальных уравнений с разделенными переменными можно отнести следующие из них:
y 2 3 d y = sin x d x , e y d y = ( x + sin 2 x ) d x
Для того, чтобы прийти от ДУ с разделяющимися переменными к ДУ с разделенными переменными, необходимо разделить обе части уравнения на произведение f 2 ( y ) ⋅ g 1 ( x ) . Так мы придем к уравнению f 1 ( y ) f 2 ( y ) d y = g 2 ( x ) g 1 ( x ) d x . Преобразование можно будет считать эквивалентным в том случае, если одновременно f 2 ( y ) ≠ 0 и g 1 ( x ) ≠ 0 . Если хоть одно из условий не будет соблюдаться, мы можем потерять часть решений.
В качестве примеров дифференциальных уравнений с разделяющимися переменными можно привести следующие из них: d y d x = y · ( x 2 + e x ) , ( y 2 + a r c cos y ) · sin x · y ‘ = cos x y .
К уравнениям с разделяющимися переменными мы можем прийти от ряда дифференциальных уравнений других видов путем замены переменных. Например, мы можем подставить в исходное уравнение z = a x + b y . Это позволит нам перейти к дифференциальному уравнению с разделяющимися переменными от дифференциального уравнения вида y ‘ = f ( a x + b y ) , a , b ∈ R .
Подставив z = 2 x + 3 y в уравнение y ‘ = 1 e 2 x + 3 y получаем d z d x = 3 + 2 e z e z .
Заменив z = x y или z = y x в выражениях y ‘ = f x y или y ‘ = f y x , мы переходим к уравнениям с разделяющимися переменными.
Если произвести замену z = y x в исходном уравнении y ‘ = y x · ln y x + 1 , получаем x · d z d x = z · ln z .
В ряде случаев прежде, чем производить замену, необходимо произвести преобразования исходного уравнения.
Предположим, что в условии задачи нам дано уравнение y ‘ = y 2 — x 2 2 x y . Нам необходимо привести его к виду y ‘ = f x y или y ‘ = f y x . Для этого нам нужно разделить числитель и знаменатель правой части исходного выражения на x 2 или y 2 .
Нам дано уравнение y ‘ = f a 1 x + b 1 y + c 1 a 2 x + b 2 y + c 2 , a 1 , b 1 , c 1 , a 2 , b 2 , c 2 ∈ R .
Для того, чтобы привести исходное уравнение к виду y ‘ = f x y или y ‘ = f y x , нам необходимо ввести новые переменные u = x — x 1 v = y — y 1 , где ( x 1 ; y 1 ) является решением системы уравнений a 1 x + b 1 y + c 1 = 0 a 2 x + b 2 y + c 2 = 0
Введение новых переменных u = x — 1 v = y — 2 в исходное уравнение y ‘ = 5 x — y — 3 3 x + 2 y — 7 позволяет нам получить уравнение вида d v d u = 5 u — v 3 u + 2 v .
Теперь выполним деление числителя и знаменателя правой части уравнения на u . Также примем, что z = u v . Получаем дифференциальное уравнение с разделяющимися переменными u · d z d u = 5 — 4 z — 2 z 2 3 + 2 z .
Подробный разбор теории и алгоритмов решения задач мы привели в разделе «Дифференциальные уравнения с разделяющимися переменными».
Линейные неоднородные дифференциальные уравнения первого порядка y ‘ + P ( x ) · y = Q ( x )
Приведем примеры таких уравнений.
К числу линейных неоднородных дифференциальных уравнений 1 -го порядка относятся:
y ‘ — 2 x y 1 + x 2 = 1 + x 2 ; y ‘ — x y = — ( 1 + x ) e — x
Для решения уравнений этого вида применяется метод вариации произвольной постоянной. Также мы можем представить искомую функцию у в виде произведения y ( x ) = u ( x ) v ( x ) . Алгоритмы применения обоих методов мы привели в разделе «Линейные неоднородные дифференциальные уравнения первого порядка».
Дифференциальное уравнение Бернулли y ‘ + P ( x ) y = Q ( x ) y a
Приведем примеры подобных уравнений.
К числу дифференциальных уравнений Бернулли можно отнести:
y ‘ + x y = ( 1 + x ) e — x y 2 3 ; y ‘ + y x 2 + 1 = a r c t g x x 2 + 1 · y 2
Для решения уравнений этого вида можно применить метод подстановки z = y 1 — a , которая выполняется для того, чтобы свести исходное уравнение к линейному дифференциальному уравнению 1 -го порядка. Также применим метод представления функции у в качестве y ( x ) = u ( x ) v ( x ) .
Алгоритм применения обоих методов приведен в разделе «Дифференциальное уравнение Бернулли». Там же можно найти подробный разбор решения примеров по теме.
Уравнения в полных дифференциалах P ( x , y ) d x + Q ( x , y ) d y = 0
Если для любых значений x и y выполняется ∂ P ( x , y ) ∂ y = ∂ Q ( x , y ) ∂ x , то этого условия необходимо и достаточно, чтобы выражение P ( x , y ) d x + Q ( x , y ) d y представляло собой полный дифференциал некоторой функции U ( x , y ) = 0 , то есть, d U ( x , y ) = P ( x , y ) d x + Q ( x , y ) d y . Таким образом, задача сводится к восстановлению функции U ( x , y ) = 0 по ее полному дифференциалу.
Выражение, расположенное в левой части записи уравнения ( x 2 — y 2 ) d x — 2 x y d y = 0 представляет собой полный дифференциал функции x 3 3 — x y 2 + C = 0
Для более подробного ознакомления с теорией и алгоритмами решения примеров можно обратиться к разделу «Уравнения в полных дифференциалах».
Видео:13. Как решить дифференциальное уравнение первого порядка?Скачать
Дифференциальные уравнения второго порядка
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами y ‘ ‘ + p y ‘ + q y = 0 , p , q ∈ R
Линейное однородное дифференциальное уравнение с постоянными коэффициентами обычно решается достаточно просто. Нам необходимо найти корни характеристического уравнения k 2 + p k + q = 0 . Здесь возможны три варианта в зависимости от различных p и q :
- действительные и различающиеся корни характеристического уравнения k 1 ≠ k 2 , k 1 , k 2 ∈ R ;
- действительные и совпадающие k 1 = k 2 = k , k ∈ R ;
- комплексно сопряженные k 1 = α + i · β , k 2 = α — i · β .
Значения корней характеристического уравнения определяет, как будет записано общее решение дифференциального уравнения. Возможные варианты:
- y = C 1 e k 1 x + C 2 e k 2 x ;
- y = C 1 e k x + C 2 x e k x ;
- y = e a · x · ( C 1 cos β x + C 2 sin β x ) .
Пример 13
Предположим, что у нас есть линейное однородное дифференциальное уравнение 2 -го порядка с постоянными коэффициентами y ‘ ‘ + 3 y ‘ = 0 . Найдем корни характеристического уравнения k 2 + 3 k = 0 . Это действительные и различные k 1 = — 3 и k 2 = 0 . Это значит, что общее решение исходного уравнения будет иметь вид:
y = C 1 e k 1 x + C 2 e k 2 x ⇔ y = C 1 e — 3 x + C 2 e 0 x ⇔ y = C 1 e — 3 x + C 2
Восполнить пробелы в теоретической части и посмотреть подробный разбор примеров по теме можно в статье «Линейные однородные дифференциальные уравнения 2 -го порядка с постоянными коэффициентами».
Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами y ‘ ‘ + p y ‘ + q y = f ( x ) , p , q ∈ R
Основным способом решение уравнений данного вида является нахождение суммы общего решения y 0 , которое соответствует линейному однородному дифференциальному уравнению y ‘ ‘ + p y ‘ + q y = 0 , и частного решения y
исходного уравнения. Получаем: y = y 0 + y
Способ нахождения y 0 мы рассмотрели в предыдущем пункте. Найти частное решение y
мы можем методом неопределенных коэффициентов при определенном виде функции f ( x ) , которая расположена в правой части записи исходного выражения. Также применим метод вариации произвольных постоянных.
К числу линейных неоднородных дифференциальных уравнений 2 -го порядка с постоянными коэффициентами относятся:
y ‘ ‘ — 2 y ‘ = ( x 2 + 1 ) e x ; y ‘ ‘ + 36 y = 24 sin ( 6 x ) — 12 cos ( 6 x ) + 36 e 6 x
Теоретические выкладки и подробный разбор примеров по теме можно найти в разделе «ЛНДУ 2 -го порядка с постоянными коэффициентами».
Линейные однородные дифференциальные уравнения (ЛОДУ) y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = 0 и линейные неоднородные дифференциальные уравнения (ЛНДУ) второго порядка y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = f ( x )
Линейные однородные и неоднородные дифференциальные уравнения и постоянными коэффициентами являются частными случаями дифференциальных уравнений этого вида.
На некотором отрезке [ a ; b ] общее решение линейного однородного дифференциального уравнения y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = 0 представлено линейной комбинацией двух линейно независимых частных решений y 1 и y 2 этого уравнения, то есть, y = C 1 y 1 + C 2 y 2 .
Частные решения мы можем выбрать из систем независимых функций:
1 ) 1 , x , x 2 , . . . , x n 2 ) e k 1 x , e k 2 x , . . . , e k n x 3 ) e k 1 x , x · e k 1 x , . . . , x n 1 · e k 1 x , e k 2 x , x · e k 2 x , . . . , x n 2 · e k 2 x , . . . e k p x , x · e k p x , . . . , x n p · e k p x 4 ) 1 , c h x , s h x
Однако существуют примеру уравнений, для которых частные решения не могут быть представлены в таком виде.
Возьмем для примера линейное однородное дифференциальное уравнение x y ‘ ‘ — x y ‘ + y = 0 .
Общее решение линейного неоднородного дифференциального уравнения y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = f ( x ) мы можем найти в виде суммы y = y 0 + y
, где y 0 — общее решение соответствующего ЛОДУ, а y
частное решение исходного дифференциального уравнения. Найти y 0 можно описанным выше способом. Определить y
нам поможет метод вариации произвольных постоянных.
Возьмем для примера линейное неоднородное дифференциальное уравнение x y ‘ ‘ — x y ‘ + y = x 2 + 1 .
Более подробно этот раздел освещен на странице «Линейные дифференциальные уравнения второго порядка».
Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Дифференциальные уравнения высших порядков
Дифференциальные уравнения, допускающие понижение порядка
Мы можем провести замену y ( k ) = p ( x ) для того, чтобы понизить порядок исходного дифференциального уравнения F ( x , y ( k ) , y ( k + 1 ) , . . . , y ( n ) ) = 0 , которое не содержит искомой функции и ее производных до k — 1 порядка.
В этом случае y ( k + 1 ) = p ‘ ( x ) , y ( k + 2 ) = p ‘ ‘ ( x ) , . . . , y ( n ) = p ( n — k ) ( x ) , и исходное дифференциальное уравнение сведется к F 1 ( x , p , p ‘ , . . . , p ( n — k ) ) = 0 . После нахождения его решения p ( x ) останется вернуться к замене y ( k ) = p ( x ) и определить неизвестную функцию y .
Дифференциальное уравнение y ‘ ‘ ‘ x ln ( x ) = y ‘ ‘ после замены y ‘ ‘ = p ( x ) станет уравнением с разделяющимися переменными y ‘ ‘ = p ( x ) , и его порядок с третьего понизится до первого.
В уравнении, которое не содержит аргумента х и имеет вид F ( y , y ‘ , y ‘ ‘ , . . . , y ( n ) ) = 0 , порядок может быть заменен на единицу следующим образом: необходимо провести замену d y d x = p ( y ) , где p ( y ( x ) ) будет сложной функцией. Применив правило дифференцирования, получаем:
d 2 y d x 2 = d p d y d y d x = d p d y p ( y ) d 3 y d x 3 = d d p d y p ( y ) d x = d 2 p d y 2 d y d x p ( y ) + d p d y d p d y d y d x = = d 2 p d y 2 p 2 ( y ) + d p d y 2 p ( y )
Полученный результаты подставляем в исходное выражение. При этом мы получим дифференциальное уравнение, порядок которого на единицу меньше, чем у исходного.
Рассмотрим решение уравнения 4 y 3 y ‘ ‘ = y 4 — 1 . Путем замены d y d x = p ( y ) приведем исходное выражение к уравнению с разделяющимися переменными 4 y 3 p d p d y = y 4 — 1 .
Более подробно решения задач по теме рассмотрены в разделе «Дифференциальные уравнения, допускающие понижение порядка».
Линейные однородные и неоднородные дифференциальные уравнения высших порядков с постоянными коэффициентами y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = 0 и y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = f ( x )
Решение уравнений данного вида предполагает выполнение следующих простых шагов:
- находим корни характеристического уравнения k n + f n — 1 · k n — 1 + . . . + f 1 · k + f 0 = 0 ;
- записываем общее решение ЛОДУ y 0 в стандартной форме, а общее решение ЛНДУ представляем суммой y = y 0 + y
— частное решение неоднородного дифференциального уравнения.
Нахождение корней характеристического уравнения подробно описано в разделе «Решение уравнений высших степеней». Для нахождения y
целесообразно использовать метод вариации произвольных постоянных.
Линейному неоднородному ДУ с постоянными коэффициентами y ( 4 ) + y ( 3 ) — 5 y ‘ ‘ + y ‘ — 6 y = x cos x + sin x соответствует линейное однородное ДУ y ( 4 ) + y ( 3 ) — 5 y ‘ ‘ + y ‘ — 6 y = 0 .
Более детальный разбор теории и примеров по теме вы можете найти на странице « Линейные однородные и неоднородные дифференциальные уравнения высших порядков с постоянными коэффициентами».
Линейные однородные и неоднородные дифференциальные уравнения высших порядков y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 1 ( x ) · y ‘ + f 0 ( x ) · y = 0 и y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 1 ( x ) · y ‘ + f 0 ( x ) · y = f ( x )
Найти решение ЛНДУ высших порядков можно благодаря сумме y = y 0 + y
, где y 0 — общее решение соответствующего ЛОДУ, а y
— частное решение неоднородного дифференциального уравнения.
y 0 представляет собой линейную комбинацию линейно независимых функций y 1 , y 2 , . . . , y n , каждая из которых является частным решением ЛОДУ, то есть, обращает равенство y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 1 ( x ) · y ‘ + f 0 ( x ) · y = 0 в тождество. Частные решения y 1 , y 2 , . . . , y n обычно подбираются из известных систем линейно независимых функций. Подобрать их далеко не всегда просто и возможно, в этом и заключается основная проблема.
После того, как мы найдем общее решение ЛОДУ, найти частное решение соответствующего ЛНДУ можно благодаря методу вариации произвольных постоянных. Итак, y = y 0 + y
Получить более подробную информацию по теме можно в разделе «Дифференциальные уравнения высших порядков».
Видео:18+ Математика без Ху!ни. Дифференциальные уравнения. Однородное уравнение.Скачать

Системы дифференциальных уравнений вида d x d t = a 1 x + b 1 y + c 1 d y d t = a 2 x + b 2 y + c 2
Данная тема подробно разобрана на странице «Системы дифференциальных уравнений». Там же приведены примеры задач с подробных разбором.
🔍 Видео
Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Линейное дифференциальное уравнение первого порядка (1-x^2)*y'-xy=1Скачать

Метод ЭйлераСкачать

Откуда появляются дифференциальные уравнения и как их решатьСкачать

Дифференциальные уравнения 1-го порядка.Скачать

2. Дифференциальные уравнения с разделяющимися переменными. Часть 1.Скачать

Численное решение задачи Коши методом ЭйлераСкачать

Математика без ху!ни. Интегралы, часть 1. Первообразная. Дифференцирование и интегрирование.Скачать