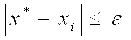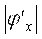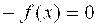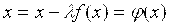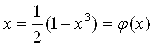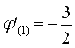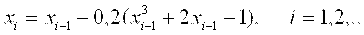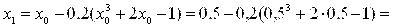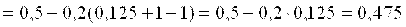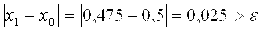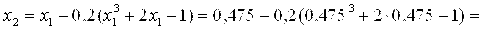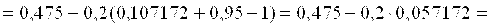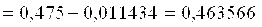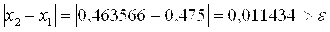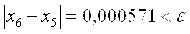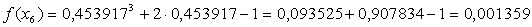Правила ввода функции
- Примеры
≡ x^2/(1+x)
cos 2 (2x+π) ≡ (cos(2*x+pi))^2≡ x+(x-1)^(2/3)
На рис.1а, 1б в окрестности корня |φ′(x)| 1, то процесс итерации может быть расходящимся (см. рис.2).
Видео:Решение нелинейного уравнения методом простых итераций (программа)Скачать

Достаточные условия сходимости метода итерации
Процесс нахождения нулей функции методом итераций состоит из следующих этапов:
- Получить шаблон с омощью этого сервиса.
- Уточнить интервалы в ячейках B2 , B3 .
- Копировать строки итераций до требуемой точности (столбец D ).
Примечание: столбец A — номер итерации, столбец B — корень уравнения X , столбец C — значение функции F(X) , столбец D — точность eps .
Видео:1 3 Решение нелинейных уравнений методом простых итерацийСкачать

3.2.1. Метод простых итераций (метод последовательных приближений)
Метод реализует стратегию постепенного уточнения значения корня.
Постановка задачи. Дано нелинейное уравнение (3.1). Корень отделен x* Î [a;b]. Требуется уточнить корень с точностью ε.
Уравнение ( 3.1) преобразуем к эквивалентному виду x=φ(x), (3.7)
Что можно сделать всегда и притом множеством способов.
Выберем начальное приближение x0Î [a;b].
Вычислим новые приближения:
Xi=φ(xi-1) , i=1,2,… где i − номер итерации. (3.8)
Последовательное вычисление значений xi по формуле (3.8) называется итерационным процессом метода простых итераций, а сама формула — формулой итерационного процесса метода.
Если 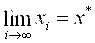
Условие сходимости 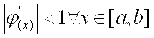
Точное решение x* получить невозможно, так как требуется Бесконечный Итерационный процесс.
Можно получить Приближенное Решение, прервав итерационный (3.8) при достижении условия
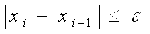
Где ε — заданная точность; i — номер последней итерации.
В большинстве случаев условие завершения итерационного процесса (3.10) обеспечивает близость значения xi к точному решению:
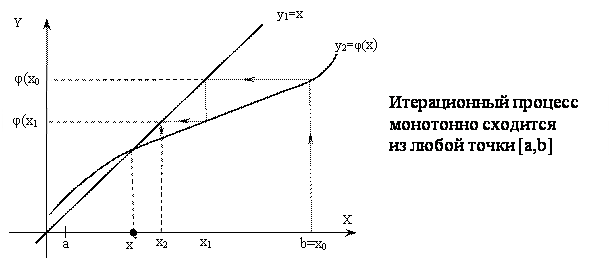
Рассмотрим геометрическую иллюстрацию метода простых итераций.
Уравнение (3.7) представим на графике в виде двух функций: y1 = x и y2= φ(x).
Возможные случаи взаимного расположения графиков функций, и соответственно, видов итерационного процесса показаны на рис. 3.7 – 3.10.
Рис. 3.7 Итерационный процесс для случая 0 1 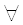
 |
Рис. 3.10 Итерационный процесс для случая 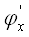
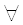
Из анализа графиков следует, что скорость сходимости растет при уменьшении значения
Метод достаточно прост, обобщается на системы уравнений, устойчив к погрешности округления (она не накапливается).
При разработке алгоритма решения нелинейного уравнения методом простых итераций следует предусмотреть защиту итерационного процесса от зацикливания: использовать в качестве дополнительного условия завершения итерационного процесса превышение заданного максимального числа итераций.
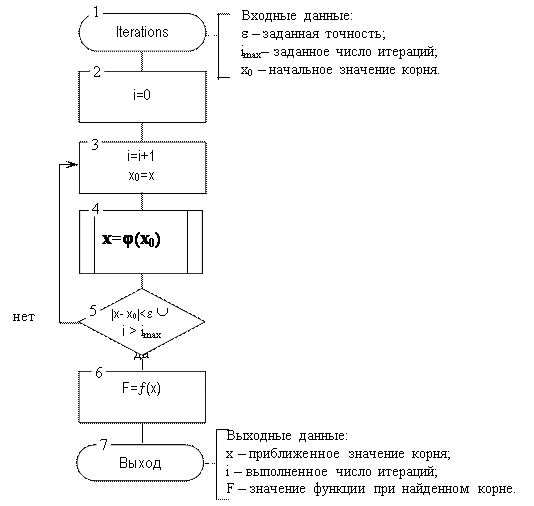 |
Рис 3.11. Алгоритм решения нелинейного уравнения методом
простых итераций:
Основной проблемой применения метода является обеспечение сходимости итерационного процесса: нужно найти такое эквивалентное преобразование (3.1) в (3.7), чтобы обеспечивалось условие сходимости (3.9) .
Простейшие эквивалентные преобразования, например:
F(x) = 0 => x+f(x) = x, т. е. φ(x) = x + f(x)
Или выразить явно x из (3.1)
F(x) = 0 => x — φ(x) = 0 => x = φ(x)
Не гарантируют сходимость.
Рекомендуется следующий способ получения формулы Сходящегося итерационного процесса.
Пусть 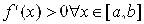
Если это не так, переписать уравнение (3.1) в виде
Умножить обе части уравнения на 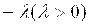
Константу l вычислить по формуле:
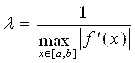
Такое значение λ гарантирует сходящийся итерационный процесс по формуле
Xi = xi+1− λ f(x) (3.12)
Где i=1,2,… — номер итерации, x0Î[a, b] – начальное приближение.
Методом простых итераций уточнить корень уравнения x3=1-2 x с точностью ε=0,001. Корень отделен ранее (см. пример 3.1), x* Î [0;1].
Сначала нужно получить формулу сходящегося итерационного процесса.
Из уравнения выразим явно x:
Проверим условия сходимости для полученной формулы:
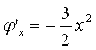
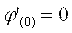
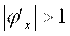
Условие сходимости не соблюдается, полученная формула не позволит уточнить корень.
Воспользуемся описанным выше способом получения формулы итерационного процесса (формулы 3.11, 3.12).
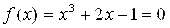
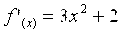
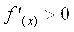
Наибольшее значение 
Следовательно 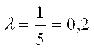
Формула Сходящегося итерационного процесса
Уточним корень с помощью данной формулы.
Выберем начальное приближение на [0;1], например x0=0,5 (середина отрезка).
Вычислим первое приближение
Проверим условие завершения итерационного процесса
Расчет следует продолжить.
X6 = 0,453917 − ответ, т. к.
Проверим полученное значение, подставив в исходное уравнение:
Значение f(x) близко к 0 с точностью, близкой к ε, следовательно, корень уточнен правильно.
Видео:Метод простых итераций пример решения нелинейных уравненийСкачать

Итерационное уточнение корней.
На этапе отделения корней решается задача отыскания возможно более узких отрезков 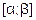
Этап уточнения корня имеет своей целью вычисление приближенного значения корня с заданной точностью. При этом применяются итерационные методы вычисления последовательных приближений к корню: x0, x1, . xn, …, в которых каждое последующее приближение xn+1вычисляется на основании предыдущего xn. Каждый шаг называется итерацией. Если последовательность x0, x1, . xn, …при n ® ¥ имеет предел, равный значению корня 
Существуют различные способы отделения и уточнения корней, которые мы рассмотрим ниже.
Отделение корней
Корень 
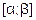
Графическое отделение корней
Графическое отделение корнейосновано на графическом способе решения уравнений – отыскании точек, в которых функция f(x)пересекает ось 0Х.
Пример 1.2.2-1. Отделить корни уравнения ln (x-1) 2 – 0.5 = 0.
На рис. 1.2.2-1 изображен график функции y = ln (x-1) 2 – 0.5, из которого следует, что уравнение имеет два действительных корня 

 |
В некоторых случаях удобно вначале преобразовать функцию f(x) к виду f(x)=g1(x)— g2(x), из которого, при условии f(x)=0, следует, что g1(x)=g2(x). При построении графиков y1=g1(x)и y2=g2(x)находят отрезки, содержащие точки пересечения этих графиков.
Пример 1.2.2-2. Отделить корни уравнения сos(x) – x + 1 = 0.
Приведем исходное уравнение к виду сos(x)= x – 1. Построив графики функций y1 = сos(x) и y2 = х – 1 (рис. 1.2.2), выделим отрезок, содержащий корень 
 |
Аналитическое отделение корней
Аналитическое отделениекорней основано на следующей теореме.
Если функция f(x) непрерывна и монотонна на отрезке [a;b] и принимает на концах отрезка значения разных знаков, то на отрезке [a;b] содержится один корень уравнения f(x)=0.
Действительно, если условия теоремы выполнены, как это имеет место на отрезке [a;b] (рис. 1.2.2-3), то есть f(a)∙f(b) 0 для xÎ [a;b], то график функции пересекает ось 0Х только один раз и, следовательно, на отрезке [a;b] имеется один корень 
Аналогично можно доказать единственность корня 
 |
Таким образом, для отделения корней нелинейного уравнения необходимо найти отрезки, в пределах которых функция монотонна и изменяет свой знак. Принимая во внимание, что непрерывная функция монотонна в интервалах между критическими точками, при аналитическом отделении корней уравнения можно рекомендовать следующий порядок действий:
1)установить область определения функции;
2)определить критические точки функции, решив уравнение f¢(x)=0;
3)составить таблицу знаков функции f(x) в критических точках и на границах области определения;
4)определить интервалы, на концах которых функция принимает значения разных знаков.
Пример 1.2.2-3. Отделить корни уравнения x — ln(x+2) = 0.
Область допустимых значений функции f(x) = x — ln(x+2) лежит в интервале (-2; ∞), найденных из условия x+2>0. Приравняв производную f¢(x)=1-1/(x+2) к нулю, найдем критическую точку хk= -1. Эти данные сведены в табл. 1.2.2-1 и табл. 1.2.2-2 знаков функции f(x).
Таблица 1.2.2-1 Таблица 1.2.2-.2
| x | x→-2 | -1 | x→∞ | x | -1.9 | -1.1 | -0.9 | 2.0 |
| Sign(f(x)) | + | — | + | Sign(f(x)) | + | — | — | + |
Уравнение x — ln(x+2) = 0 имеет два корня 



Уточнение корней
Задача уточнения корня уравнения 



Метод половинного деления
Пусть корень уравнения f(x)=0 отделен на отрезке 
Метод половинного деления позволяет получить последовательность вложенных друг в друга отрезков [a1;b1], [a2;b2], …,[ai;bi],…, [an;bn], таких что f(ai).f(bi) 3 +x-1=0 с точностью 
Результаты удобно представить с помощью таблицы 1.2.3-3.
| k | a | b | f(a) | f(b) | (a+b)/2 | f((a+b)/2) | a k | b k |
| -1 | 0.5 | -0.375 | 0.5 | |||||
| 0.5 | -0.375 | 0.75 | 0.172 | 0.5 | 0.75 | |||
| 0.5 | 0.75 | -0.375 | 0.172 | 0.625 | -0.131 | 0.625 | 0.75 | |
| 0.625 | 0.75 | -0.131 | 0.172 | 0.688 | 0.0136 | 0.625 | 0.688 |
После четвертой итерации длина отрезка |b4-a4| = |0.688-0.625| = 0.063 стала меньше величины e, следовательно, за приближенное значение корня можно принять значение середины данного отрезка: x = (a4+b4)/2 = 0.656.
Значение функции f(x) в точке x = 0.656 равно f(0.656) = -0.062.
Метод итерации
Метод итераций предполагает замену уравнения f(x)=0 равносильным уравнением x=j(x). Если корень уравнения отделен на отрезке [a;b], то исходя из начального приближения x0Î[a;b], можно получить последовательность приближений к корню
x1 = j(x0), x2 = j(x1), …, 
где функция j(x) называется итерирующей функцией.
Условие сходимости метода простой итерации определяется следующей теоремой.
Пусть корень х* уравнения x=j(x) отделен на отрезке [a;b]и построена последовательность приближений по правилу xn=j(xn-1). Тогда, если все члены последовательности xn=j(xn-1) Î [a;b] и существует такое q (0 -1. Таким образом, очевидно, что если |j’(x)| 1. На рис. 1.2.3-4а показан случай, когда j’(x)>1, а на рис. 1.2.3-4b – когда j’(x)
📹 Видео
Метод Ньютона (метод касательных) Пример РешенияСкачать

Метод простой итерации Пример РешенияСкачать

Метод итерацийСкачать

Алгоритмы С#. Метод простых итерацийСкачать

10 Численные методы решения нелинейных уравненийСкачать

Метод простых итераций - PascalСкачать

Численное решение уравнений, урок 1/5. Локализация корняСкачать
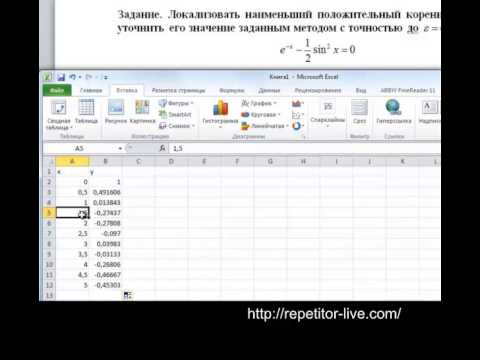
8 Метод простой итерации Ручной счет Решение системы линейных уравнений СЛАУСкачать

Отделение корней уравнений аналитическим методом. Уточнение корней методом половинного деленияСкачать

Решение слау методом итераций. Метод простых итераций c++.Скачать

Метод половинного деления решение нелинейного уравненияСкачать

Алгоритмы. Нахождение корней уравнений методом деления отрезка пополам.Скачать

Как найти корни уравнения в Excel с помощью Подбора параметраСкачать

4.2 Решение систем нелинейных уравнений. МетодыСкачать

2.2 Итерационные методы решения СЛАУ (Якоби, Зейделя, релаксации)Скачать

Алгоритмы. Нахождение корней уравнения методом хордСкачать

Метод итераций (последовательных приближений)Скачать

 ≡ x^2/(1+x)
≡ x^2/(1+x)