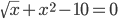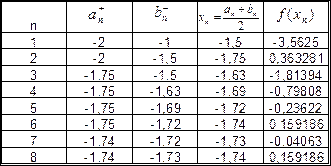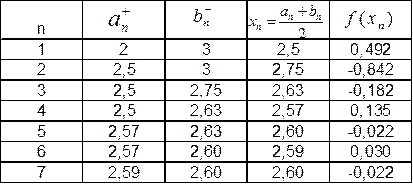Видео:Метод половинного деленияСкачать
Метод половинного деления (метод дихотомии или метод бисекции)
Теорема 2. Итерационный процесс половинного деления сходится к искомому корню ξ с любой наперед заданной точностью ε.
Доказательство: Рассмотрим последовательность чисел ξi являющихся приближением корня на i -ом шаге.
ξi=½(bi+ai), i=0,1.
где a0=a; b0=b; ai;bi — границы подынтервалов, в которых f(ai)f(bi) 0 мы ни задали, всегда можно найти такое n , что 
ч.т.д.
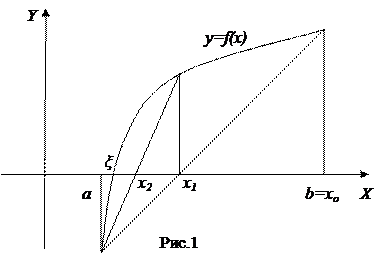
Графически метод дихотомии выглядит следующим образом
|f(c)|≤δ f(a)f(c) 10 = 1024 ≈ 10 3 раз. За 20 итераций (n=2) уменьшается в 2 20 ≈ 10 6 раз.
Пример №1 . Найти экстремум функции: y=5x 2 -4x+1 методом дихотомии, если ε=0.1, а исходный интервал [0,10].
- Решение
- Видео решение
Пример №3 . Методом бисекции найти решение нелинейного уравнения на отрезке [a,b] с точностью ε = 10 -2 . Выбрав полученное решение в качестве начального приближения, найти решение уравнения методом простой итерации с точностью ε = 10 -4 . Для метода простой итерации обосновать сходимость и оценить достаточное для достижения заданной точности число итераций.
sqrt(t)+x 2 = 10, a = 2.6, b = 3
Найдем корни уравнения: 
Используем для этого Метод половинного деления (метод дихотомии)..
Считаем, что отделение корней произведено и на интервале [a,b] расположен один корень, который необходимо уточнить с погрешностью ε.
Итак, имеем f(a)f(b) 1 /2(a+b) и вычисляем f(c). Проверяем следующие условия:
1. Если |f(c)| 1 /2 n (b-a)
В качестве корня ξ. возьмем 1 /2(an+bn). Тогда погрешность определения корня будет равна (bn – an)/2. Если выполняется условие:
(bn – an)/2 1 /2(an+bn).
Решение.
Поскольку F(2.6)*F(3) 0, то a=2.8
Итерация 2.
Находим середину отрезка: c = (2.8 + 3)/2 = 2.9
F(x) = 0.113
F(c) = -0.487
Поскольку F(c)•F(x) 0, то a=2.825
Остальные расчеты сведем в таблицу.
| N | c | a | b | f(c) | f(x) |
| 1 | 2.6 | 3 | 2.8 | -1.6275 | -0.4867 |
| 2 | 2.8 | 3 | 2.9 | -0.4867 | 0.1129 |
| 3 | 2.8 | 2.9 | 2.85 | 0.1129 | -0.1893 |
| 4 | 2.8 | 2.85 | 2.825 | -0.1893 | -0.3386 |
| 5 | 2.825 | 2.85 | 2.8375 | -0.3386 | -0.2641 |
| 6 | 2.8375 | 2.85 | 2.8438 | -0.2641 | -0.2267 |
Ответ: x = 2.8438; F(x) = -0.2267
Решение было получено и оформлено с помощью сервиса Метод Ньютона онлайн
Пример №2 . Локализовать корень нелинейного уравнения f(x) = 0 и найти его методом бисекции с точностью ε1 = 0,01. Выбрав полученное решение в качестве начального приближения, найти решение уравнения методом простой итерации с точностью ε2 = 0,0001. Для метода простой итерации обосновать сходимость и оценить достаточное для достижения заданной точности ε2 число итераций.
Видео:Метод половинного деления. ДихотомияСкачать
Метод половинного деления для решения уравнений по математике
Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только возрастает. Метод половинного деления (метод дихотомии/метод бисекции) отличается от других стандартных методов тем, что для него не требуется выполнять условие, [1 и 2] производная сохраняют знак на интервале [[a, b].] Данного рода метод применяют для любых непрерывных функций [f(x),] включая не дифференцируемые.
Решение уравнений методом половинного деления сводится к следующим действиям:
1. Определить новое приближение корня х в середине отрезка [[а,b]:] [х=frac];
2. Найти значения функции в точках [а, х: F(a) и F(x);]
3. Проверить условие [F(a)*F(x)
Наш искусственный интеллект решает сложные математические задания за секунды.
Мы решим вам контрольные, домашние задания, олимпиадные задачи с подробными шагами. Останется только переписать в тетрадь!
Видео:Отделение корней уравнений аналитическим методом. Уточнение корней методом половинного деленияСкачать
Метод половинного деления. Один из методов уточнения корней уравнения (1) – метод половинного деления
Один из методов уточнения корней уравнения (1) – метод половинного деления. Исходные данные: уравнение f(x)=0; отрезок [a,b], на котором существует единственный корень уравнения (корень отделен), т.е. f(x) удовлетворяет условиям: f(x) непрерывна на [a,b], монотонна нем и f(a)f(b) 0 (знаки функции f(x) в точках a и c одинаковы), то левый конец отрезка заменяется на середину (а=с) иначе правый конец заменяется на середину (b=c).
4. Если длина отрезка не превосходит заданной точности (b-a 4 -x 3 -2x 2 +3x-3=0.
Полагая f(x)= x 4 -x 3 -2x 2 +3x-3, имеем f’(x)=4x 3 -3x 2 -4x+3.
Найдем нули производной: 4x 3 -3x 2 -4x+3=0; 4x(x 2 -1)-3(x 2 -1)=0;(x 2 -1)(4x-3)=0;
Составим таблицу знаков функции f(x):
| x | -∞ | -1 | 3/4 | +∞ | |
| f(x) | + | — | — | — | + |
Из таблицы видно, что уравнение имеет два действительных корня x1 
(-∞;-1) и x2 (1;+ ∞). Уменьшим промежутки, на которых находятся корни, до единичной длины:
| x | -2 | -1 | ||
| f(x) | + | — | — | + |
Следовательно, x1 (-2;-1) и x2 (1;2).
Уточним один из корней, например, x1, методом половинного деления до сотых долей. Все вычисления удобно производить, используя следующую таблицу:
Второй корень, уточняемый аналогичным образом, равен 1,73.
2. Отделить корни графически и уточнить их методом половинного деления.
Перепишем уравнение в виде 
. Обозначим 
, 
и построим графики этих функций:
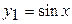
Из рисунка видно, что уравнение имеет три корня: точный x=0 и еще два, расположенных симметрично на отрезках [-3;-2] и [2;3].
Уточним корень на отрезке [2;3]:
Задания
1)Отделить корни аналитически и уточнить их методом половинного деления до 0,01, используя электронные таблицы.
1. 3x 4 +4x 3 -12x 2 -5=0
2. 2x 3 -9x 2 -60x+1=0
5. 3x 4 +3x 3 +6x 2 -10=0
7. x 4 +4x 3 -3x 2 -17=0
8. x 4 -x 3 -2x 2 +3x-3=0
9. 3x 4 +4x 3 -12x 2 +1=0
10. 3x 4 -8x 3 -18x 2 +2=0
11. 2x 4 -3x 3 +8x 2 -1=0
12. 2x 4 +8x 3 +3x 2 -1=0
13. x 4 -4x 3 -8x 2 +1=0
14. 3x 4 +4x 3 -12x 2 -5=0
15. 2x 3 -8x 2 -30x+1=0
17. 2x 4 -2x 2 -7=0
18. 3x 4 +8x 3 +6x 2 -10=0
19. x 4 -18x 2 +6=0
20. x 4 +4x 3 -3x-7=0
21. x 4 -2x 3 -x 2 +3x-3=0
22. 3x 4 +4x 3 -3x 2 -17=0
23. 2x 4 -5x 3 -12x 2 +2=0
24. 3x 4 +9x 3 -14x 2 +1=0
25. x 4 +2x 3 -x-1=0
26. x 4 +8x 3 -6x 2 -72x=0
28. x 4 -3x 2 +75x-10000=0
2) Отделить корни графически и уточнить их методом половинного деления до 0.01, используя электронные таблицы.
Лабораторная работа №3
Решение нелинейных уравнений методом хорд
Краткая теория
Будем рассматривать уравнения вида f(x)=0 (1). Пусть корень уравнения отделен и находится на отрезке [a,b]. Уточним этот корень методом хорд. Геометрически метод хорд означает замену на отрезке [a,b] графика функции y=f(x) хордой, проведенной через точки (a,f(a)) и (b,f(b)):
Здесь ξ — точный корень уравнения (1), x 
— начальное приближение к корню, x 
-точка пересечения хорды с осью Ох – первое приближение к корню. Далее метод хорд применяется на отрезке [a, x ] и получается второе приближение к корню — x 
. В случае, изображенном на рис.1, конец отрезка а остается неподвижным. Из уравнения хорды и условия, что точка (x ,0) принадлежит хорде, получается формула для вычисления n-го приближения к корню для случая, когда а – неподвижный конец: x =b,
x 
=a- 
(2)
Для случая неподвижного конца b используется формула: x =a,
x =x 
— 
(3)
Правило определения неподвижного конца хорды:
Если знаки первой и второй производных функции f(x) на отрезке [a, b] совпадают, то неподвижным являются конец b, иначе — конец a.
Метод хорд обеспечивает на n-м шаге абсолютную погрешность приближения к корню уравнения (1), не превосходящую длину n-го отрезка: 
1. Определить, какой конец отрезка будет неподвижным и принять за x другой конец отрезка.
2. Вычислить новое приближение к корню x по формуле (2) или (3).
3. Если длина отрезка [x , x ] не превосходит заданной точности, то процесс заканчивается и в качестве точного корня можно взять x или x , иначе идти к п.2
Решение одного варианта
1.Отделить корни графически и уточнить их методом хорд с точностью до 0.001: tg(0.5x+0.1)=x 
.
Отделим корень графически. Построим графики функций
y =tg(0.5x+0.1) и y =x :
Таким образом, уравнение имеет два корня
x [0.5; 1] и x [-0.5; 0]
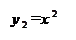
Чтобы уточнить этот корень методом хорд, определим знаки первой и второй производной функции f(x)= tg(0.5x+0.1)-x на промежутке [0.5;1]. Имеем
f ‘(x)=0.5/cos (0.5x+0.1)-2x;
3. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. x lgx — 1.2 = 0
14. 1.8x 2 – sin10x = 0
15. ctgx – x / 4 = 0
16. tg(0.3x + 0.4) = x 2
17. x – 20sinx = 0
18. ctgx – x / 3 = 0
19. tg(0.47x + 0.2) = x 2
20. x 2 + 4sinx = 0
21. ctgx – x / 2 = 0
22. 2x – lgx – 7 = 0
24. 3x – cosx – 1 = 0
26. 10cosx-0,1x 2 =0
2)Отделить корни аналитически и уточнить их методом хорд до 0.001:
🔥 Видео
6 Метод половинного деления C++ Численные методы решения нелинейного уравненияСкачать
Алгоритмы. Нахождение корней уравнений методом деления отрезка пополам.Скачать
Урок 10. C++ Метод половинного деленияСкачать
Метод половинного деления - ВизуализацияСкачать
7 Метод половинного деления Mathcad Численные методы решения нелинейного уравненияСкачать
Решение нелинейного уравнения методом деления отрезка пополамСкачать
Метод Ньютона (метод касательных) Пример РешенияСкачать
Метод дихотомииСкачать
Метод дихотомии c++Скачать
Решение уравнений (метод дихотомии) на C#Скачать
Алгоритмы. Нахождение корней уравнения методом хордСкачать
Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать
Численное решение уравнений, урок 3/5. Метод хордСкачать
ОГЭ №21 Как решать кубическое уравнение x^3+4x^2-9x-36=0 Группировка Деление многочлена столбикомСкачать
1 3 Решение нелинейных уравнений методом простых итерацийСкачать
ЕГЭ по математике. Деление многочлена на двучленСкачать
Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать
