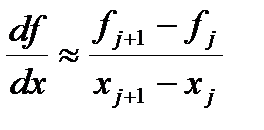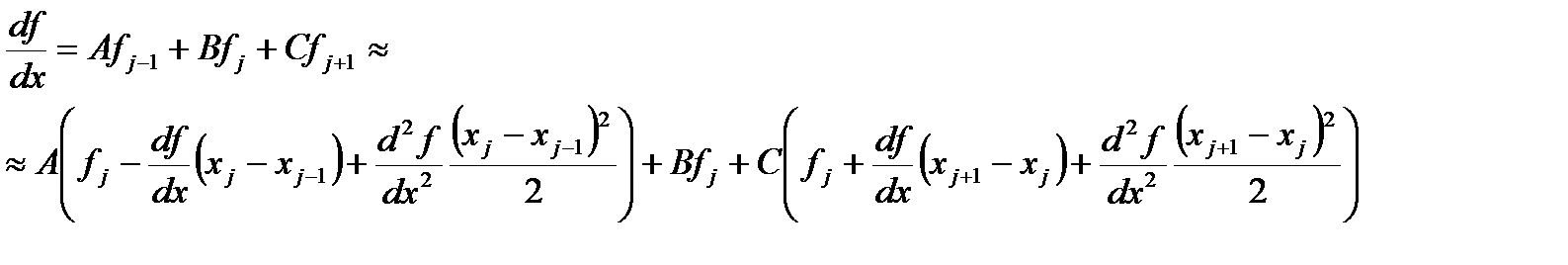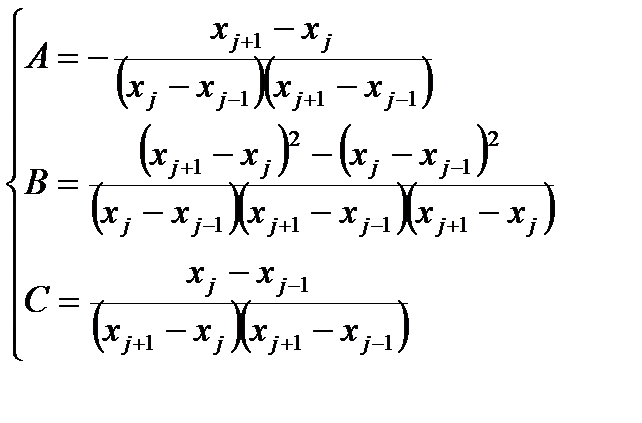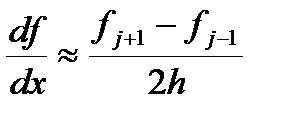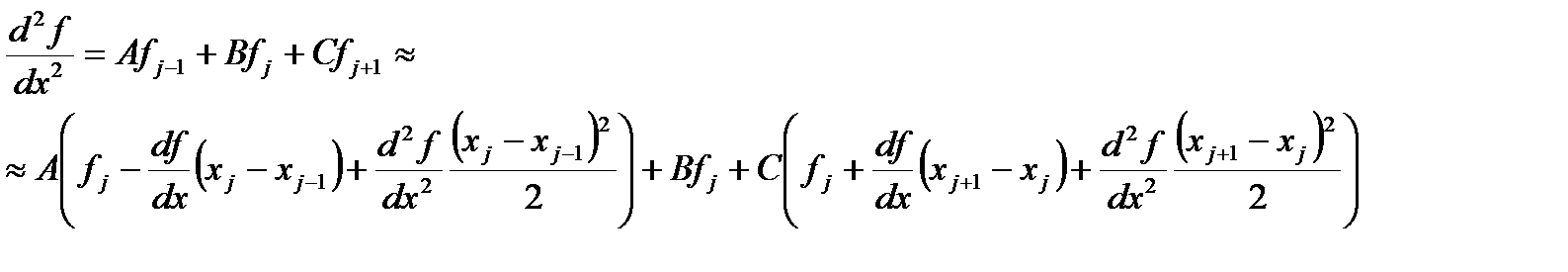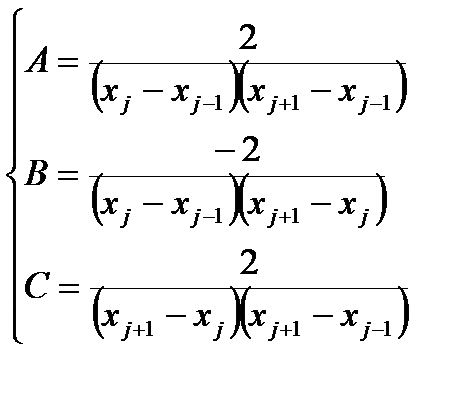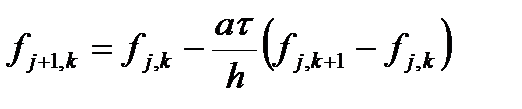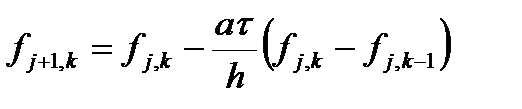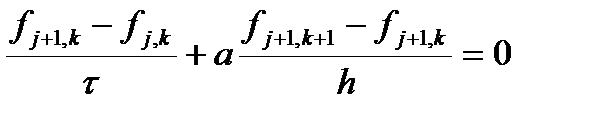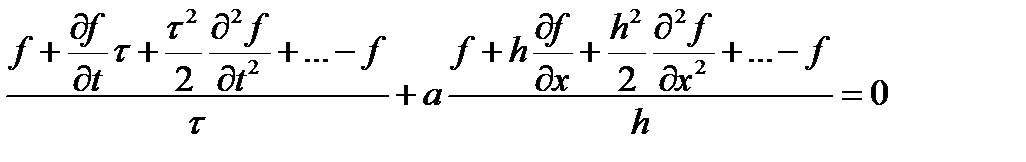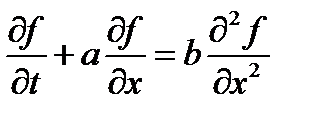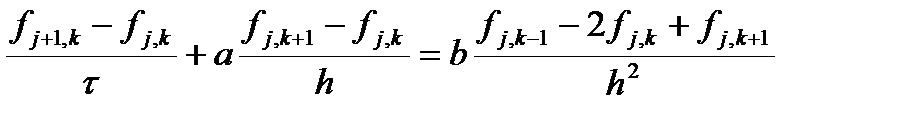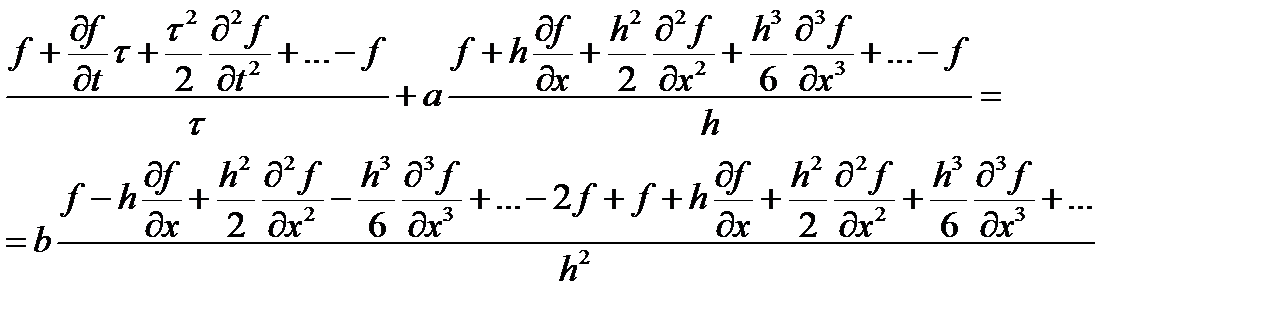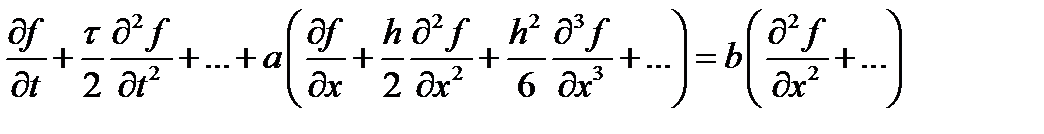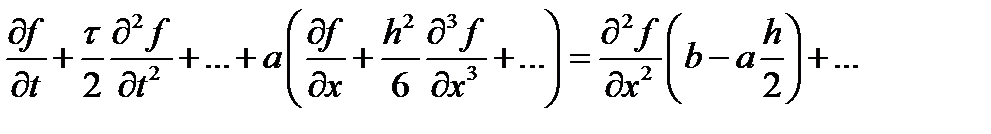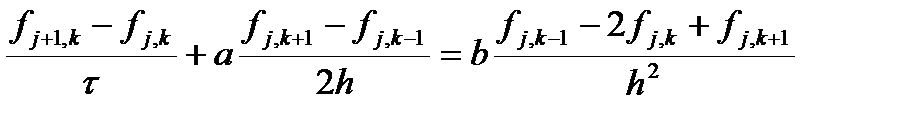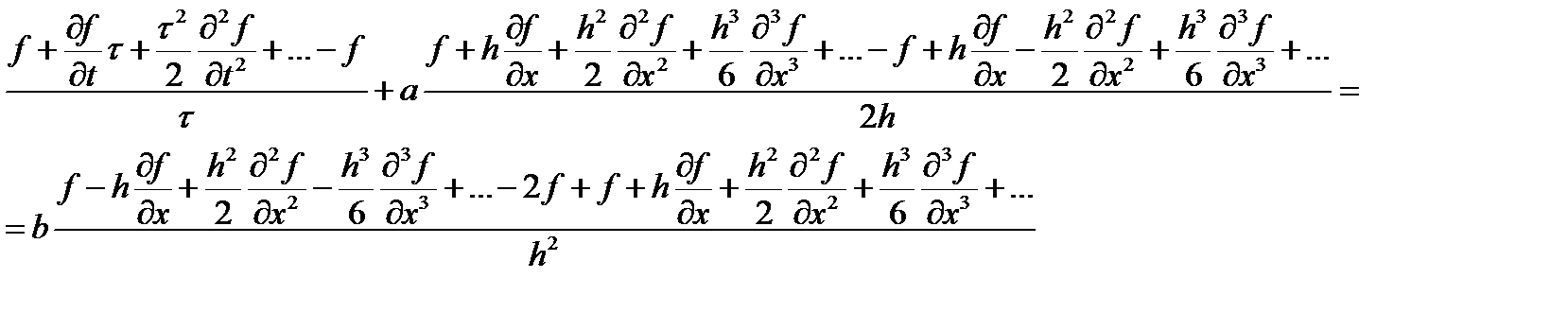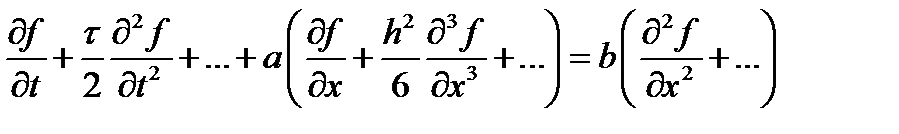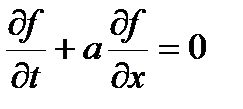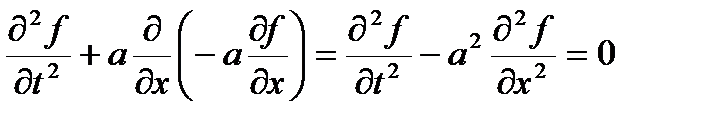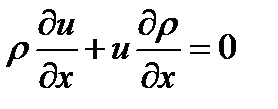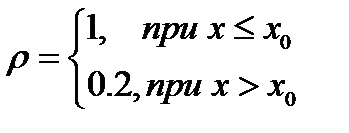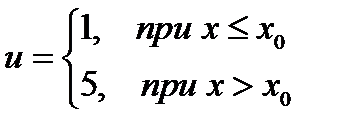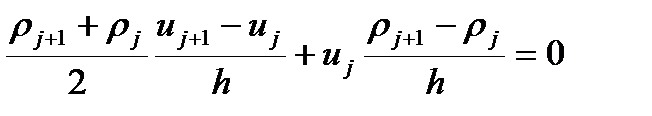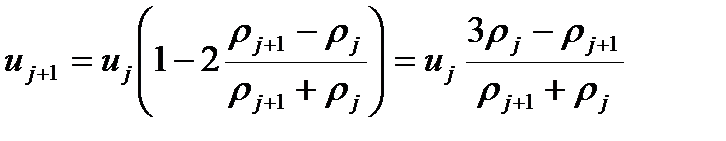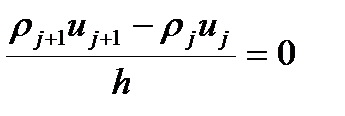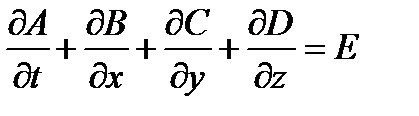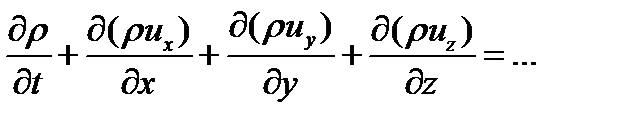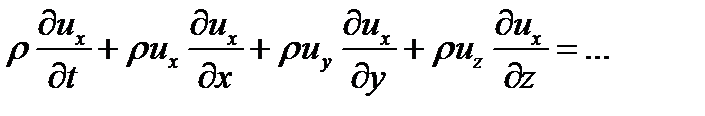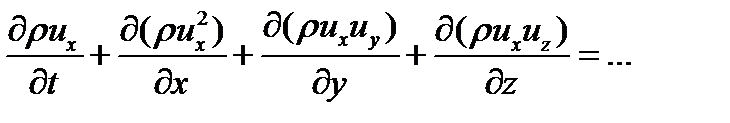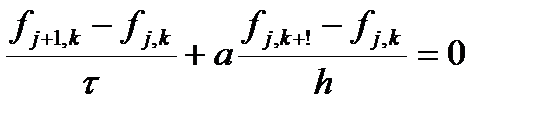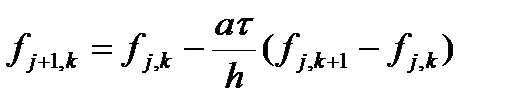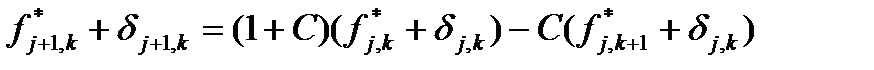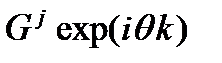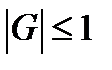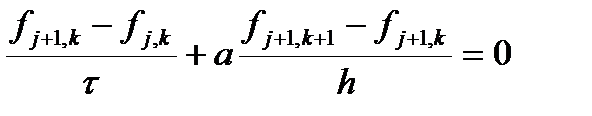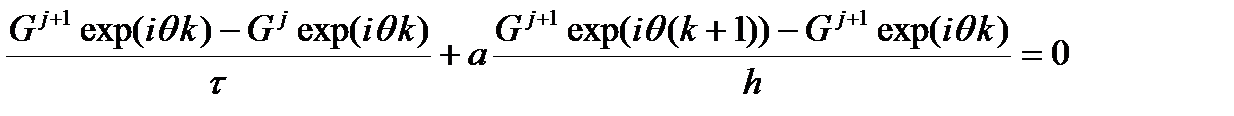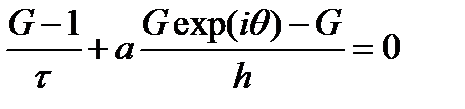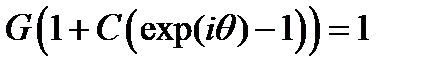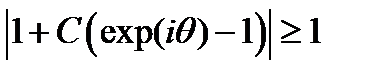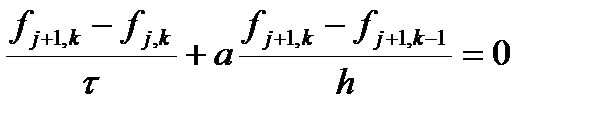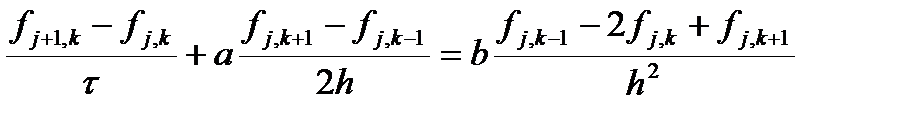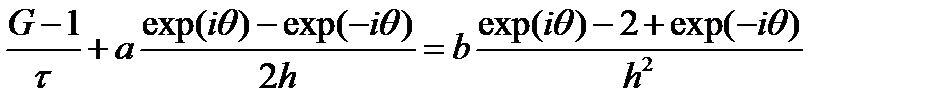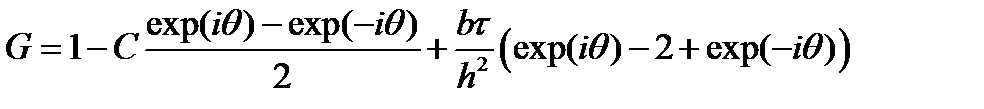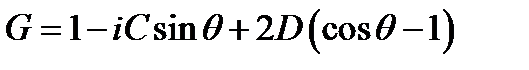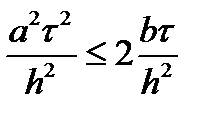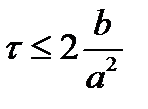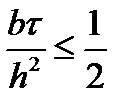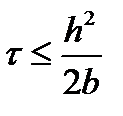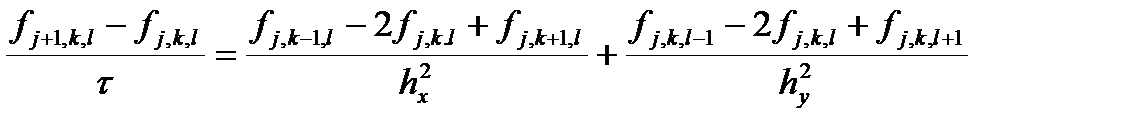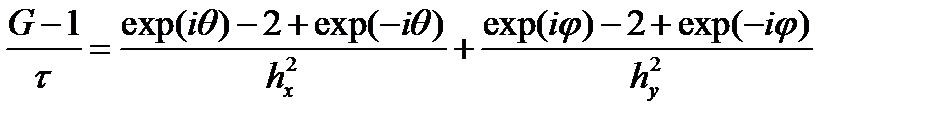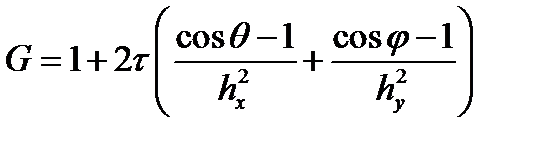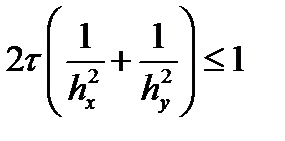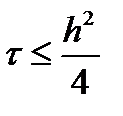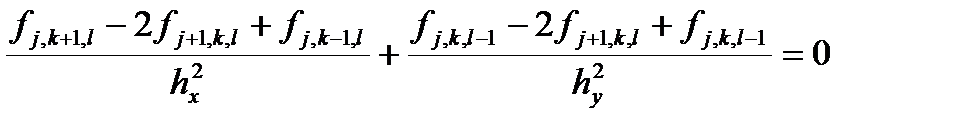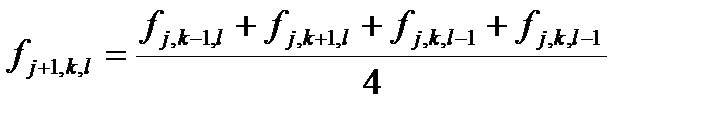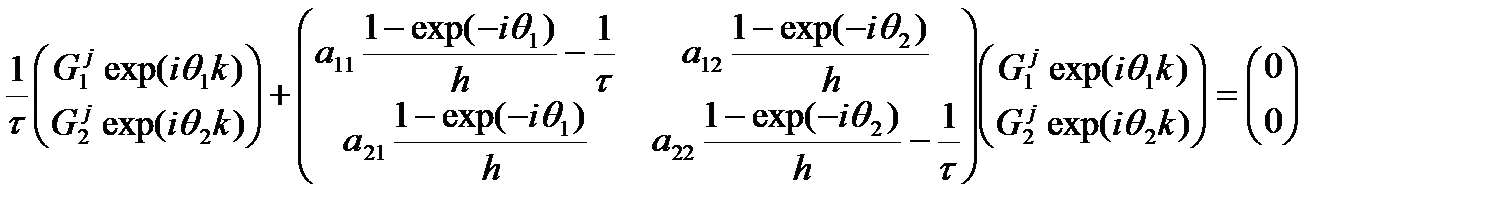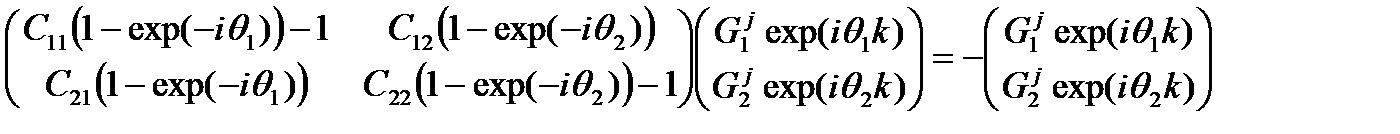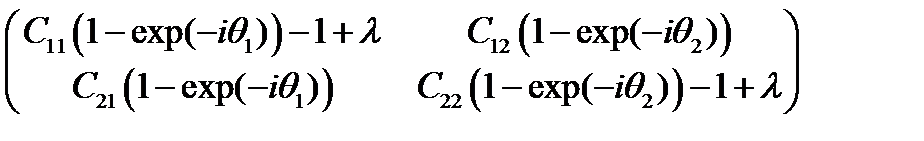Методом конечных разностей сформировать систему разностных уравнений

Достоинство этих методов состоит в том, что они сводят решение краевой задачи для дифференциального уравнения к решению системы алгебраических уравнений относительно значений искомой функции на заданном множестве точек. Это достигается заменой производных, входящих в дифференциальное уравнение, их конечно-разностными аппроксимациями.

Рассмотрим сущность такого метода решения для дифференциального уравнения второго порядка (1.41) при заданных граничных условиях (1.42). Разобьем отрезок [0,1] на n равных частей точками xi= ih(i= 0,1. , n). Решение краевой задачи (1.41), (1.42) сведем к вычислению значений сеточной функции yi в узловых точках xi. Для этого напишем уравнение (1.42) для внутренних узлов:

(1.49)

Заменим производные, входящие в эти соотношения, их конечно-разностными аппроксимациями:

(1.50)

Подставляя эти выражения в (1.49), получаем систему разностных уравнений:

(1.51)

являющуюся системой n-1 алгебраических уравнений относительно значений сеточной функции Входящие в данную систему y0 (при i = 1) и уп (при i = п — 1) берут из граничных условий (1.42):

На практике часто граничные условия задают в более общем виде (1.38):

(1.52)

В этом случае граничные условия также должны представляться в разностном виде путем аппроксимации производных Y‘(0) и Y‘(1) с помощью конечно-разностных соотношений. Если использовать односторонние разности (соответствующий шаблон показан на рис. 1.7, а),при которых производные аппроксимируются с первым порядком точности, то разностные граничные условия примут вид

(1.53)

Из этих соотношений легко находятся значения y0, yn.

Однако, как правило, предпочтительнее аппроксимировать производные, входящие в (1.52), со вторым порядком точности с помощью центральных разностей:

Рис. 1.7. Аппроксимация граничных условий

В данные выражения входят значения сеточной функции и yn+1 в так называемых фиктивных узлах х=1-hи х =1+h, лежащих вне рассматриваемого отрезка (рис. 1.7, б). В этих узлах значения искомой функции также должны быть найдены. Следовательно, количество неизвестных значений сеточной функции увеличивается на два. Для замыкания системы привлекают еще два разностных уравнения (1.51) при i = 0, i = п.

Аппроксимировать граничные условия со вторым порядком можно и иначе (см. рис. 1.7, в). В этом случае используют аппроксимации:

Таким образом, решение краевой задачи для дифференциального уравнения сведено к решению системы алгебраических уравнений вида (1.51). Эта система является линейной или нелинейной в зависимости от того, линейно или нелинейно дифференциальное уравнение (1.41). Методы решения таких систем рассмотрены ранее.

Рассмотрим подробнее один частный случай, который представляет интерес с точки зрения практических приложений и позволяет проследить процесс построения разностной схемы. Решим краевую задачу для линейного дифференциального уравнения второго порядка

(1.54)

с граничными условиями вида

Разобьем отрезок [0,1] на части с постоянным шагом h с помощью узлов . Аппроксимируем вторую производную Y²конечно-разностным соотношением (1.50). При этом значения искомой функции в узлах Y(xi) приближенно заменяем соответствующими значениями сеточной функции yi. Записывая уравнение (1.54) в каждом узле с использованием указанных аппроксимаций, получаем

Обозначим рi, fiсоответственно величины . После несложных преобразований приведем последнее равенство к виду

(1.56)

Получилась система n—1 линейных уравнений, число которых совпадает с числом неизвестных значений сеточной функции в узлах. Ее значения на концах отрезка определены граничными условиями (1.55):

Решив систему уравнений (1.56) с учетом условий (1.57), найдем значения сеточной функции, которые приближенно равны значениям искомой функции. Покажем, что такое решение существует и сходится к точному решению при h→ 0.

Для доказательства существования решения рассмотрим систему линейных уравнений (1.56). Ее матрица является трехдиагональной; на главной диагонали находятся элементы . Поскольку р(х) > 0, то pi > 0, и диагональные элементы матрицы преобладают над остальными, так как в каждой строке модули этих элементов больше суммы модулей двух остальных элементов, каждый из которых равен единице. При выполнении этого условия решение системы линейных уравнений существует и единственно.

Что касается сходимости решения, то здесь имеет место следующее утверждение.

Утверждение. Если функции р(х) и f(x) дважды непрерывно дифференцируемы, то при h→0 разностное решение равномерно сходится к точному со скоростью O(h2).

Это — достаточное условие сходимости метода конечных разностей для краевой задачи (1.54), (1.55).

Система линейных алгебраических уравнений (1.56) с трехдиагональной матрицей может быть решена методом прогонки. При этом условие р(х) > 0 гарантирует выполнение условия устойчивости прогонки.

Этот метод на практике используется также и при р(х) Будет полезно почитать по теме:

Видео:6.3 Решение разностных уравненийСкачать

Метод конечных разностей

Существует множество численных методов решения дифференциальных уравнений. Некоторые из них ищут решение в виде аналитических функций. Однако, для случаев со сложной геометрией или разрывами в граничных условиях такие методы становятся довольно громоздкими. Поэтому большинство численных методов решения дифференциальных уравнений рассматривают дискретно заданные («сеточные») функции, т.е. функции, заданные на некотором множестве точек, называемом сеткой.

Поговорим о сетках. В одномерном случае от сетки остается лишь конечное множество точек, заданное на отрезке, на котором ищется решение. Точки могут располагаться равномерно или неравномерно. В многомерном случае наблюдается огромное многообразие типов сеток. Приведем лишь несколько примеров. Ниже на рисунках представлены равномерные прямоугольная и треугольная сетки.

Сетки бывают неравномерными (часто линии сетки сгущают в той области, где хотят поднять точность расчета).

Сетки бывают адаптивными (например, сетка, являющаяся прямоугольной в некоторой системе координат, связанной с поверхностью).

Правильный подбор типа и параметров сетки может существенно (в отдельных случаях на порядки) сократить ресурсы, требуемые для получения результата.

Точки пересечения линий сетки называются узлами. Элементарные области, ограниченные линиями сетки (плоскостями или иными поверхностями в трехмерном случае) называются ячейками. Значения искомой функции могут задаваться либо в узлах сетки, либо в каких-либо точках (например, в центрах) ячеек.

Численные методы решения дифференциальных уравнений, работающие с сеточными функциями, сводят исходную задачу к решению системы алгебраических уравнений. Одним из самых распространенных методов является метод конечных разностей[4]. Ему будет посвящена значительная часть данного курса. Не потому, что он лучший. Просто когда-то он был самым распространенным и по нему написано огромное количество книг, в которых изложены все трудности, которые встречаются и в других методах. Например, можно почитать книжки [9, 10]. Как правило, для метода конечных разностей используют прямоугольные сетки. Значения функции рассчитываются в узлах сетки.

Аппроксимация

Итак, требуется заменить имеющиеся уравнения их дискретными аналогами. Такой процесс называется дискретизацией уравнений. Рассмотрим производные по x (производные по другим переменным записываются совершенно аналогично). Отсортируем дискретные значения переменной x по возрастанию и проиндексируем их. Значения производных в узле сетки приближенно записываются (аппроксимируются) через значения функции в данном и ближайших узлах. Обязательное условие: приближенное значение производной, посчитанное по дискретному аналогу, должно стремиться к точному значению при стремлении расстояния между узлами к нулю. Минимальное количество точек, необходимое для аппроксимации n-й производной, равно n+1. Так, первую производную можно приближенно найти, зная значение функции в 2 точках, вторую производную – в 3 точках.

Самым распространенным способом дискретизации является разложение функции в ряд Тейлора. При выводе дискретного аналога производной используются только несколько первых членов ряда (остальные полагаются равными нулю). Порядком аппроксимации называется порядок последней учитывающейся производной в ряде Тейлора[5]. Рассмотрим простейшую аппроксимацию первой производной. В точке с номером j ее можно получить двумя способами.

Первая из этих формул называется аппроксимацией разностью вперед, вторая – аппроксимацией разностью назад. Это формулы первого порядка. Попробуем написать формулу второго порядка.

Для равномерных сеток (x_j+1-x_j)=(x_j-x_j-1). Обычно шаг сетки при этом обозначают через h. При этом запись дискретного аналога первой производной существенно упрощается

В этом случае принято говорить, что первая производная аппроксимируется центральной разностью. Аналогично записываются дискретные аналоги для второй производной.

Для равномерной сетки получаем

Далее, чтобы избежать громоздких выражений, будем рассматривать только равномерные сетки.

При записи дискретного аналога дифференциальных уравнений возникает уже гораздо большее разнообразие вариантов. Рассмотрим волновое дифференциальное уравнение первого порядка.

Оно описывает распространение волны (перенос массы или заряда) со скоростью a. Как указывалось выше к таким уравнениям можно свести гиперболические уравнения. Будем рассматривать именно такой случай. Считаем, что мы идем маршевым методом по времени. Нам известно распределение функции по x в некоторый момент времени и нужно найти распределение в следующий момент. Рассмотрим аппроксимации первого порядка. Значения функции в узлах сетки будем обозначать f_,jk, где первый индекс относится к значению времени, а второй – координаты. Производную по времени аппроксимируем выражением

где t — шаг по времени. А производную по координате можно аппроксимировать как разностями вперед, так и разностями назад. Получаем первые две возможные аппроксимации.

Для наглядности часто рисуют графические изображения разностных схем, называемые шаблонами. Приведем шаблоны двух описанных формул. На рисунках считается, что координата x идет горизонтально слева направо, а ось y направлена вертикально снизу вверх.

Строгих стандартов на шаблоны не существует. Например, часто рисуют стрелки из узлов, где значения известны, в узел (узлы), где значения неизвестны. Часто в одной книге шаблоны нарисованы в разных местах в разных стилях. Здесь, тоже не будем придерживаться одного стиля.

За приведенные графические изображения рассмотренные схемы часто называют «правый уголок» и «левый уголок». В обеих этих схемах на новом (по времени) слое используется лишь один узел, следовательно, значение в этом узле можно явным образом выразить через значения в других узлах.

Такие схемы называются явными. Зная значения на j-м слое, легко получаются значения на j+1-м слое. Если производную по координате выписать на новом слое, то получим две неявные схемы.

Они имеют следующие шаблоны

В случае неявной схемы мы получаем не конечную формулу для значения функции в узле, а связи между неизвестными значениями в узлах на новом слое. Перебрав все значения индекса k мы получаем систему (линейных) алгебраических уравнений, которую надо решить для получения искомых значений. В рассматриваемом случае можно отделаться малой кровью. Каждое уравнение будет связывать два соседних узла. Найдя значение в каком-либо узле на новом слое, легко получить значение в соседнем. Далее, двигаясь по цепочке, получаем значения во всех узлах на новом слое. Таким образом, нужно знать хотя бы одно значение. Его можно взять из граничного условия. В общем случае в неявных схемах без специальных ухищрений не удается обойтись без решения системы уравнений.

Посмотрим, что мы реально считаем методом конечных разностей. Выберем схему «правый уголок». Разложим искомую функцию в ряд Тейлора в окрестности точки с индаксами j и k и учтем члены со второй производной. Итак, имеем

после сокращения получаем, то, что решаем реально

То есть, дискретизация привела к тому, что, надеясь решить одно уравнение, получаем решение другого уравнения. Радует лишь то, что с уменьшением шагов по времени и по пространству разница между уравнениями уменьшается. Тем не менее, при любых ненулевых шагах реально решаемое уравнение может не только иметь иные (по сравнению с исходным) свойства, но даже принадлежать к другому типу. Например, исходное рассматриваемое уравнение предполагает, что волна движется в пространстве не меняя своей формы. Для демонстрации зададим в качестве начального распределения разрывное распределение (см. случай а на рисунке ниже). Если неудачно выбрана расчетная схема или ее параметры, то можно получить решения, показанные на том же рисунке с обозначениями б и в, или вообще не получить никакого разумного решения.

Теперь рассмотрим параболическое уравнение, а именно цветовое уравнение

(Как отмечалось выше, такое название оно получило за то, что описывает, в том числе, распространение подкрашенной жидкости в воде.) Параметр a определяет скорость конвективного переноса концентрации (или, например, температуры), а параметр b определяет диффузию (теплопередачу). Выберем явную схему. Первую производную по пространству для начала аппроксимируем с помощью правой разности. Получаем дискретный аналог дифференциального уравнения

Как и раньше разложим функцию в ряд Тейлора, но по пространству учтем третью производную.

после сокращений получаем

теперь сгруппируем вторые производные по x. Получим

То есть получается, что мы не только решаем другое уравнение, но и коэффициенты в нем другие. Коэффициент b имеет физический смысл коэффициента диффузии (теплопроводности, вязкости) и не может быть отрицательным. А у нас получилось, что при 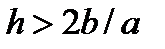коэффициент диффузии становится отрицательным, что не соответствует никакой физике. Добавку к коэффициенту диффузии (теплопроводности, вязкости) принято называть сеточной (или схемной) диффузией (теплопроводностью, вязкостью).

Теперь рассмотрим случай, когда первая производная аппроксимируется центральной разностью. Получаем дискретный аналог дифференциального уравнения

Как и раньше разложим функцию в ряд Тейлора, но по пространству учтем третью производную.

после сокращений получаем

По сравнению с исходным уравнением присутствуют член, пропорциональный первой степени шага по времени, и член, пропорциональный второй степени шага по пространству. В таком случае говорят, что данная схема имеет второй порядок аппроксимации по простронству и первый – по времени. В целом, когда говорят о порядке аппроксимации уравнения, под порядком понимают наименьший из порядков аппроксимации по всем переменным. В данном случае мы имеем аппроксимацию первого порядка.

Для линейных уравнений есть «точные» оценки погрешности расчета. Но при моделировании плазмы, как правило, приходится иметь дело с нелинейными уравнениями. Для них точных оценок нет. Для оценки точности расчета обычно проводят два (иногда больше) расчета на разных сетках. Если на второй сетке шаги по всем переменным вдвое меньше, чем на первой, и схема имеет первый порядок аппроксимации, то погрешность уменьшится примерно вдвое. «Примерно» потому, что в разложении в ряд Тейлора существуют члены с производными более высоких порядков и, соответственно, с более высокими степенями шагов. Таким образом, разница между результатами расчетов будет примерно соответствовать погрешности расчета с более мелкой сеткой. Если использовалась аппроксимация второго порядка, то уменьшение шагов вдвое приводит к уменьшению погрешности примерно в четыре раза.

Следует отметить, что для таких оценок необходимо пропорционально изменять и шаг по времени и шаг по пространству. Если уменьшать только один из шагов, оставляя другой без изменения, то погрешность может как увеличиваться, так и возрастать. Объясняется это тем, что погрешность зависит и от соотношения шагов. Для того, чтобы это наглядно показать, составим дифференциальное приближение волнового уравнения первого порядка. От проделанных выше операций эта процедура отличается исключением высших производных по времени из реально решаемых уравнений. Итак, рассматриваем уравнение

используя следующую разностную схему

.

Для этого случая мы ранее уже получили выражение

.

Чтобы выразить вторую производную по времени через производные по пространству продифференцируем исходное уравнение по времени. Получаем

.

Выразим первую производную по времени через исходное уравнение

Теперь реально решаемое уравнение можно записать в виде

.

Полученный результат называется дифференциальным приближением рассматриваемой разностной схемы. Из него видно, что наименьшую погрешность можно получить, задав шаги, связанные соотношением

Как показано выше, члены, отвечающие за погрешность в реально решаемых уравнениях, пропорциональны некоторым производным от искомой функции. Но в природе, в том числе и в плазме, могут существовать области с очень большими градиентами. Часто проще их описать разрывными функциями. Значения производных в этих областях очень велики (для разрывов – бесконечны), следовательно, и погрешность численного решения может быть недопустимо большой. Простого универсального метода обхода этой неприятности для произвольной системы дифференциальных уравнений нет. Но для уравнений магнито-гидродинамики такой способ есть. Рассмотрим две эквивалентные записи уравнения, описывающего перенос массы (или заряда) вдоль оси

Будем считать, что распределение плотности вдоль оси нам известно. Причем плотность задана разрывной функцией

Пусть x₀>0, u(0)=1. Очевидно, что аналитическое решение для скорости будет

Попробуем решить уравнение во второй форме записи методом конечных разностей. Распишем разностную схему

Выразим значение скорости в следующей точке через значение в предыдущей

Получаем, что при переходе через разрыв скорость получит новое значение 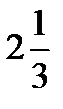. То есть расход массы (заряда) снизился примерно вдвое. Причем этот результат не зависит от шага сетки. Если мы используем первую форму записи уравнения, то схема записывается

скорость в следующей точке равна

При переходе через разрыв получаем точное решение. Чтобы избежать подобных проблем исходные уравнения, по возможности, нужно приводить к виду

То есть без коэффициентов перед производными. Такой вид называется дивиргентным. Иногда говорят о дивиргентной форме записи уравнения. Если в уравнениях магнто-гидродинамики не учитываются вязкость, диффузия и теплопроводность (т.е. процессы, при записи которых используются вторые производные), то их можно привести к дивиргентному виду. Рассмотрим правые части уравнения сохранения массы и одного из уравнений сохранения импульса

первое из них уже в дивиргентной форме. А второе можно привести к дивиргентному виду если прибавить к нему первое уравнение умноженное на u_x. Тогда получаем

Окончательно уравнение импульса переписывается в виде

Устойчивость

Итак, будем считать, что аппроксимировать дифференциальные уравнения дискретными аналогами мы научились. Но выясняется, что не каждая разностная схема, полученная в полном соответствии с теорией аппроксимации, позволяет получить разумный результат. Дело в том, что как бы точно ни были заданы начальное приближение, начальные и граничные условия, всегда найдется какая-нибудь погрешность. Как минимум будут ошибки округления. При некоторых условиях эти ошибки начинают быстро расти. В конце концов, это может привести к тому, что результат опять не будет ничего общего иметь с моделируемым процессом.

Условие, что погрешности не накапливаются, называется условием устойчивости. Существует много методов проверки различных численных схем на устойчивость. Рассмотрим два из них.

Первый способ не очень точен, применение его бывает довольно громоздким, но он интуитивно понятен и надежен. Называется методом дискретного возмущения[6]. В методе предполагается, что во всех узлах решение точное, кроме одного, в котором возмущение равно d. Далее следят за развитием этого возмущения и пытаются выяснить, при каких условиях оно нарастает.

Начнем с простого уравнения первого порядка. Рассмотрим решение волнового уравнения схемой «уголок». Итак, имеем разностную схему

откуда выражаем значение на новом слое

Безразмерный комплекс 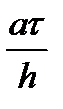называется числом Куранта и обычно обозначается C. Теперь выражение для значения на следующем слое можно записать более кратко

В силу линейности уравнения возмущения будут описываться таким же соотношением. Для доказательства представим значение в каждой точке в виде суммы точного решения реально решаемого уравнения (будем обозначать его звездочкой) и погрешности.

Вычитая из данного соотношения уравнение для точного решения получаем

δ_j+1,k=(1+C)δ_j,k-Cδ_j,k+1

Считаем, что на j-м слое все возмущения, кроме k-го, равны нулю. Возмущение в k-й точке равно d. Тогда на j+1-м слое будут два ненулевых возмущения:

Чтобы схема была устойчивой, требуется, чтобы максимальное по модулю возмущение на новом слое было меньше или равно максимальному по модулю возмущению на предыдущем слое. Из соотношения для k-1-го узла получаем: |C|£1. Из соотношения для k-го узла имеем: -2£C£0. Следовательно: -1£C£0. Теперь рассмотрим k+2-й слой. Там будут три ненулевых возмущения:

Их надо сравнить с максимальным по модулю возмущением из j+1-м. Желающие могут убедиться, что новых ограничений мы не получим. Не получим их и если рассмотреть последующие слои. Окончательно имеем: ‑1£C£0. Так как шаги по времени и по пространству положительны, то получаем, что использовать такую схему можно только при a£0. Причем шаг по времени должен удовлетворять соотношению

Все это было проделано для схемы, где производная по пространству аппроксимировалась разностью вперед. Все тоже самое можно проделать для схемы с разностью назад. Желающие могут проделать такие же выкладки. Я здесь привожу конечный результат: 0£C£1. То есть «левый уголок» для этого уравнения можно применять только при положительных a.

Применение метода дискретного возмущения для неявных схем затруднительно.

Условие |C|£1 называется условием Куранта-Фридрихса-Леви. Вообще говоря, это условие является необходимым (но не достаточным!) для всех явных схем для дифференциальных уравнений гиперболического типа.

У полученных результатов (в том числе и у условия Куранта-Фридрихса-Леви) есть несколько трактовок и интерпретаций. Рассмотрим сначала интерпретацию с помощью характеристик. Здесь полезно графическое изображение. Сначала мы рассматривали «правый уголок». Проведем характеристику через точку на новом слое. Рассмотрим неустойчивые случаи: a>0 и |C|>1. Характеристика показана на рисунке красным цветом

А теперь посмотрим, как выглядит картинка для устойчивого случая

Из рисунков очевидно следует простая интерпретация: характеристика, приходящая в точку, где мы хотим найти значение, должна пересекать отрезок, соединяющий какие-либо две другие точки в используемом шаблоне. Как отмечалось выше, характеристика идущая в точку, где нужно найти значение, должна приходить из области, где значение известно. В данном случае, такой областью является отрезок, соединяющий две точки, используемые в шаблоне (на отрезке всегда можно найти значение с помощью интерполяции).

Еще одна интерпретация условия Куранта-Фридрихса-Леви гласит: численное возмущение должно распространяться по сетке не медленнее, чем распространяется в пространстве возмущение в моделируемом процессе. Так, в рассмотренном примере возмущение, заданное в одной точке на слое, на следующем слое было уже и в соседней точке. То есть за время t оно распространилось в пространстве на расстояние h. Таким образом, скорость распространения численного возмущения составила 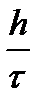. Для устойчивости эта скорость должна быть больше или равна физической скорости a. Нетрудно заметить, что это и утверждается условием Куранта-Фридрихса-Леви.

При использовании схемы «левый уголок» картинки симметричны рассмотренным. Отсюда следует простое правило: при использовании схемы типа «уголок» нужно использовать разность навстречу потоку (против потока).

Самым популярным методом исследования разностных схем на устойчивость является спектральный признак устойчивости (он же метод фон Неймана). Он точен для линейных уравнений с постоянными коэффициентами. Итак, будем искать ошибку в виде

это соответствует представлению функции ошибки в виде интеграла Фурье. При этом G отвечает за амплитуду колебаний, а q — за период колебаний. Требование устойчивости сводится к условию

при любых значениях q. Рассмотрим применение этого метода к неявным схемам типа «уголок» для волнового уравнения первой степени. Возьмем разностную схему вида

подставляем выражение для ошибки

сокращая на G j exp(iθk) получаем

из условия устойчивости получаем

Построим на комплексной плоскости возможные значения левой части полученного выражения. Геометрическое точек представляет собой окружность единичного радиуса с центром в точке -1. Выражение, стоящее под модулем, описывает окружность радиусом C с центром в точке 1-C. Таким образом, получаем следующее графическое представление

Отсюда наглядно видно, что при С=1 получаем единичную окружность, т.е. неравенство превращается в равенство. Это означает, что величина ошибки будет оставаться на прежнем уровне (не будет расти, но и не будет уменьшаться). Неравенство выполняется при С£0 и при С³1. При 0 1

Совершенно аналогично можно рассмотреть другую неявную схему

Естественно, получим устойчивость при С£-1 и при С³0. При -1 2 £|2D-C|. Все четыре возможных варианта эллипсов, соответствующих неустойчивым схемам представлены на рисунке (единичная окружность показана красным цветом).

6 b4W77YMUz9d3KiO3W2BS+e8HvYgOd/9j3Knyp8CdI20fKt3H6rutE2+b8wI71ZYhnoLC9C827k3/ dmh7D7SBnRW/ChAWF35OkAciE1z93gJ/JLH9XfTa/Crk5D8AAAD//wMAUEsDBBQABgAIAAAAIQBr gL9H3QAAAAUBAAAPAAAAZHJzL2Rvd25yZXYueG1sTI9BS8QwEIXvgv8hjODNTSy73VqbLiIoogd1 LXjNNrNtMJmUJrut/nqjF70MPN7jvW+qzewsO+IYjCcJlwsBDKn12lAnoXm7uyiAhahIK+sJJXxi gE19elKpUvuJXvG4jR1LJRRKJaGPcSg5D22PToWFH5CSt/ejUzHJseN6VFMqd5ZnQuTcKUNpoVcD 3vbYfmwPTsIy29vi5T5/+npomunxfWnW4tlIeX4231wDizjHvzD84Cd0qBPTzh9IB2YlpEfi701e kV3lwHYSVmK1Bl5X/D99/Q0AAP//AwBQSwECLQAUAAYACAAAACEAtoM4kv4AAADhAQAAEwAAAAAA AAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNdLnhtbFBLAQItABQABgAIAAAAIQA4/SH/1gAAAJQB AAALAAAAAAAAAAAAAAAAAC8BAABfcmVscy8ucmVsc1BLAQItABQABgAIAAAAIQC0jCDORgYAAF0y AAAOAAAAAAAAAAAAAAAAAC4CAABkcnMvZTJvRG9jLnhtbFBLAQItABQABgAIAAAAIQBrgL9H3QAA AAUBAAAPAAAAAAAAAAAAAAAAAKAIAABkcnMvZG93bnJldi54bWxQSwUGAAAAAAQABADzAAAAqgkA AAAA «>

Проанализировав эти ограничения, можно оставить только два из них (остальные выполнятся автоматически): 2D£C+1 и C 2 +C£2D. К ним можно добавить, что для уравнений, описывающих реальные процессы в плазме величина D всегда положительна, т.к. положительны все величины, входящие в ее определение.

Теперь рассмотрим эти ограничения с точки зрения шагов по пространству и времени. Перепишем второе ограничение в виде

разделив полученное равенство на шаг по времени и умножив на квадрат шага по пространству получаем:

После несложного преобразования получаем

Ранее было показано, что то, что стоит в левой части полученного неравенства, является коэффициентом вязкости (теплопроводности, диффузии) в реально решаемом уравнении. В правой части неравенства стоит заведомо неотрицательная величина. Таким образом, это условие устойчивости можно сформулировать так: в реально решаемом уравнении (еще точнее: в дифференциальном приближении) коэффициент вязкости (теплопроводности, диффузии) должен быть неотрицательным[7]. Это же неравенство можно рассматривать как ограничение на шаг по пространству. Таким образом, при численном решении параболических уравнений с использованием явных схем существуют не только ограничения на шаг по времени, но и ограничения на шаги по пространству.

Такое ограничение на шаг можно снять, если для аппроксимации первой производной по пространству использовать центральную разность. Ранее было показано, что коэффициент вязкости (теплопроводности, диффузии) при этом не меняется в зависимости от шага. Проверяем. Запишем разностную схему

Применим метод фон Неймана для анализа ее устойчивости.

Проведем ряд сокращений

Геометрическое место таких точек на комплексной плоскости будет представлять собой эллипс с центром в точке 1-2D. Полуось в направлении оси X равна 2D, а полуось в направлении оси Y равна С. В соответствии с условием устойчивости этот эллипс не должен выходить за пределы единичной окружности. Из рассмотрения пересечения эллипса с осями координат следует: |C|£1 и 0£D£0.5. Еще одно ограничение возникает из рассмотрения радиуса кривизны эллипса в точке касания с единичной окружностью: С 2 £2D. Подставив в последнее неравенство вместо безразмерных чисел их определения, получаем

Теперь рассмотрим ограничение на величину D

Таким образом, ограничение на шаг по пространству снято, зато появились два новых ограничения на шаг времени. Следует отметить, что одно из этих ограничений не зависит от шага по пространству и определяется только физическими величинами.

Давненько в этом тексте не упоминались эллиптические уравнения. Ранее писалось, что для их решения вводят новую переменную и сводят задачу к решению параболического уравнения. Рассмотрим, как это происходит, на примере уравнения Лапласа.

Превращаем его в параболическое уравнение

Напишем разностную схему

Применим метод фон Неймана (теперь в нем будут фигурировать две экспоненты и две переменные, отвечающие за периоды колебаний)

Применяя формулу Эйлера получаем

Схема будет устойчивой, если модуль G будет меньше единицы при любых значениях q и j. Отсюда легко получаем

Если шаги по обоим пространственным направлениям равны, то формула упрощается

Теперь рассмотрим, что станет с рассмотренной разностной схемой, если в нее подставить максимальное допустимое значение шага по времени.

Перенесем все члены из левой части в правую. Получим

Как видно, такое уравнение соответствует разностному аналогу исходного уравнения (до введения дополнительной переменной) у которого значение центрального элемента взято на новом слое. Новая переменная уже не присутствует в разностной схеме, поэтому обычно говорят не о слоях по времени, а об итерациях.

Выразим явным образом значение функции на новой итерации

В случае если шаги по разным направлениям равны, то формула становится еще проще

т.е. в этом случае новое значение функции в узле равно среднему арифметическому значений в соседних узлах.

До сих пор мы рассматривали отдельные уравнения. Теперь надо упомянуть системы уравнений. Рассмотрим простейшую систему дифференциальных уравнений.

Используем явную схему типа «уголок»

Воспользуемся спектральным методом для анализа устойчивости. Запишем в матричной форме.

Умножим на шаг по времени и перенесем первый вектор-столбец в правую часть

Вектор-столбцы представляют собой погрешности на текущем и следующем шагах по времени. Линейная алгебра учит, что существуют такие числа l, что погрешность на новом слое будет ровно в l раз больше погрешности на текущем. Критерием устойчивости при этом гласит: максимальный модуль l не должен превосходить 1. Согласно той же самой алгебре для нахождения таких чисел приравниваем нулю определитель матрицы

получаем квадратное уравнение

Это уравнение, конечно, можно решить аналитически, после чего тщательно исследовать условия устойчивости. Но в случае, когда имеется несколько нелинейных уравнений (типичная ситуация при расчетах плазмы), задача может стать нерешаемой в принципе.

Видео:6-2. Метод сетокСкачать

Конечно-разностные аппроксимации производных (стр. 1 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7

Конечно-разностные аппроксимации производных

Конечно-разностные аппроксимации производных (конечные разности) — способ приближенного вычисления частных производных

Выражения для конечных разностей можно получить из разложения функции в ряд Тейлора:

Или более коротко с использованием индексов точек:

Отсюда , где — остаток.

Отбрасывая остаток можно получить правую разность:

Погрешность такой аппроксимации определяется старшим членом в отброшенном остатке и в данном случае этот член содержит в первой степени.

Аналогичным образом, разлагая в ряд функцию можно получить:

Получим новую аппроксимацию первой производной:

которая называется левой разностью. У нее погрешность также определяется членом, содержащим в первой степени. Однако, если из выражения (1) вычесть (2), то можно получить более точную аппроксимацию первой производной, которая называется центральной разностью:

В этом случае член, определяющий погрешность аппроксимации, будет содержать во второй степени.

Аппроксимацию второй производной можно получить исходя из ее определения, — отношение приращения функции к приращению аргумента, где в качестве функции выступает аппроксимация первой производной. Также ее можно получить из выражений (1) и (2), если из (1) вычесть (2), отбросить члены содержащие производные старше второй, то получим:

Отброшенный остаток будет содержать член с во второй степени (после деления на )

Исходя из определения, можно получить выражения для третьей, четвертой и более старших разностей:

Для функции двух переменных выражения для конечных разностей, в предположении что первый индекс относится к координате , а второй — , будут выглядеть следующим образом:

правая разность по оси : ; правая разность по оси : ; левая разность по оси : ; левая разность по оси : ; центральная разность по оси : ; центральная разность по оси : ; вторая разность по оси : ; вторая разность по оси : .

Смешанная производная может быть получена следующим образом:

Алгоритм решения стационарных краевых задач методом конечных разностей

Метод конечных разностей — универсальный сеточный численный метод решения задач микроуровня.

Алгоритм решения стационарных краевых задач методом конечных разностей — последовательность действий, приводящая к решению стационарной задачи микроуровня

Нанесение на объект сетки или дискретизация пространства. Сетка — совокупность точек (узлов) дискретного пространства, аппроксимирующего непрерывное исходное пространство. Сетка выбирается таким образом, чтобы на ней легко можно было аппроксимировать производные с помощью конечных разностей. Как правило это равномерная прямоугольная сетка, но может быть и сетка заданная в полярных координатах, и неравномерная сетка, если таковая быстрее приводит к решению задачи. При наненсении сетки, если это возможно, следует учесть симметрию объекта. Это поможет сократить размерность аппроксимирующей системы уравнений. Нумерация узлов сетки. Для повышения эффективности решения в условиях использования свойства разреженности матрицы коэффициентов математической модели нумерацию следует проводить так, чтобы разность номеров соседних узлов была минимальной. Так, если двумерный объект имеет размер по оси больше, чем по оси , то нумерацию узлов нужно выполнять вдоль оси (вдоль короткой стороны). Запись разностного уравнения для каждого внутреннего узла сетки. При необходимости запись уравнений граничных условий для приграничных узлов. В результате должна быть получена замкнутая система, в общем случае, нелинейных алгебраических уравнений. Решение системы алгебраических уравнений.

Решение линейных одномерных стационарных краевых задач с помощью МКР

Предположим необходимо определить распределение температуры в стержне, теплоизолированном с цилиндрической стороны, и с заданной температурой на боковых гранях.

Одномерное стационарное уравнение теплопроводности для изотропной среды выглядит следующим образом:

В соотвествии с алгоритмом решения стационарных краевых задач методом конечных разностей наносим на объект равномерную сетку, как это показано на рис. 1.

Для каждого внутреннего узла сетки записываем разностный аналог исходного дифференциального уравнения:

для узла 1:
для узла 2:

В результате получили замкнутую систему линейных алгебраических уравнений, где неизвестными являются и , а и — известные граничные условия.

Решив систему уравнений, получим и . Это решение является точным, поскольку в исходной постановке задача линейная.

Рассмотрим теперь решение задачи с краевым условием второго рода, на правой границе стержня задан тепловой поток:

Пусть и .

Запишем разностные аналоги для внутренних узлов сетки:

для узла 1:
для узла 2

Получили незамкнутую систему алгебраических уравнений (неизвестными являются , и ), дополнить которую можно разностным аналогом краевого условия (1).

Проще всего воспользоваться левой разностью:

Решая эту систему уравнений, получим , , .

Однако можно заметить, что аппроксимация задачи во внутренних узлах имеет второй порядок точности, а на границе — первый.

Можно вспомнить, что аппроксимация первой производной с помощью центральной разности имеет второй порядок точности, но для этого необходимо, чтобы граничный узел 3 был бы центральным узлом. Используется следующий прием: вводиться дополнительный фиктивный узел за пределами области, бывший граничный узел 3 становиться как бы внутренним (см. рис. 2)

Теперь можно записать следующую систему конечно-разностных уравнений:

для узла 1:
для узла 2:
для узла 3:
граничное условие второго рода:

За повышение точности пришлось заплатить увеличением размерности системы конечно-разностных уравнений.

Решение нелинейных одномерных стационарных краевых задач с помощью МКР

Предположим необходимо определить распределение температуры в стержне, теплоизолированном с цилиндрической поверхности, и с заданной температурой на боковых гранях.

Одномерное стационарное уравнение теплопроводности для анизотропной среды выглядит следующим образом:

где — коэффициент теплопроводности.

Возможны нелинейности двух типов: коэффициент теплопроводности может зависеть от координаты (среда с неоднородными свойствами) и от температуры. Рассмотрим случай зависимости коэффициента теплопроводности от координаты на примере приближенного решения задачи об остываниии комнаты через окно с одинарным и двойным остеклением.

Предположим, что толщина стекла . Температура в комнате , на улице —

Тепловой поток на улицу пропорционален градиенту температуры, то есть .

В соотвествии с алгоритмом решения стационарных краевых задач наносим на объект равномерную сетку, в предположении, что промежуток между стеклами равен двойной толщине стекла, как это показано на рис. 1.

Для каждого внутреннего узла сетки записываем разностный аналог исходного дифференциального уравнения:

для узла 1:
для узла 2:
для узла 3:

В результате получили замкнутую систему линейных алгебраических уравнений, где неизвестными являются , и , а и — заданные граничные условия. Условно будем читать, что (реальные значения , ).

Решив систему уравнений, получим , и . В этом случае градиент температуры составит , то есть двойное остекление в 20 раз эффективнее одинарного.

В том случае, когда коэффициент теплопроводности зависит от температуры, например для металлов он пропорционален ей, придем к следующей системе нелинейных алгебраических уравнений (для сетки из четырех узлов, два из которых внутренние):

для узла 1:
для узла 2:

Данную систему придется решать итерационными методами.

Решение нестационарных одномерных задач с помощью МКР

Для решения нестационарных задач с помощью МКР используется та же идея дискретизации независимой переменной, что и при решении стационарных задач, в данном случае такой независимой переменной помимо пространства является время. На ось времени наносится сетка, в узлах которой выполняется аппроксимация частной производной по времени.

Но поскольку при этом возможны различные сочетания конечных разностей по оси координат и по времени, можно получить различные схемы решения нестационарных задач. Рассмотрим их на примере нестационарного уравнения теплопроводности:

Пусть при записи разностей нижний индекс соответствует оси , а верхний — оси времени.

Первый вариант разностного уравнения, апроксимирующего исходное (1):

называется явной разностной схемой, поскольку в этом уравнении всего одна неизвестная величина , которая может быть вычислена явным образом. Остальные переменные, входящие в уравнение (2) известны либо как начальные условия (при ), либо с предыдущего временного слоя.

Второй вариант разностного уравнения, апроксимирующего исходное (1):

называется неявной разностной схемой, поскольку в этом уравнении несколько неизвестных величин, относящихся к -му временному слою. Для их нахождения придется записать систему разностных уравнений для всех внутренних узлов сетки, и решить ее.

Графическое изображение разностных уравнений получило название шаблонов решения сответствующих задач. В данном случае на рис. 1,а представлен шаблон явной разностной схемы, а на рис. 1,б — неявной.

Рис. 1. Шаблоны явной и неявной разностной схемы

Использование шеститочечного шаблона применено в схеме Кранка-Николсона:

В общем случае использования шеститочечного шаблона, имеем схему с весами:

которая при является неявной.

Примеры решения нестационарных задач с помощью МКР

Предположим необходимо определить изменение распределения температуры в стержне во времени (изменение температурного поля), теплоизолированном с цилиндрической стороны, с заданной температурой на боковых гранях (граничные условия) и заданной температурой стержня в нулевой момент времени (начальные условия).

Решим задачу с помощью явной разностной схемы.

Одномерное нестационарное уравнение теплопроводности для изотропной среды выглядит следующим образом:

Пусть , выберем значения шага по оси и значение шага по оси времени .

Наносим на объект равномерную сетку по оси , как это показано на рис. 1.

Записываем явную разностную схему для узла 1:

где — граничное условие, — начальные условия, отсюда .

Записываем явную разностную схему для узла 2:

где — граничное условие, — начальные условия, отсюда .

Таким образом найдено температурное поле в момент времени .

Аналогично для момента времени :

Для момента времени :

Получили картину прогревания стержня в течение трех единиц времени, представленную на рис. 2.

Результат явно не соответствует физическим процессам, произошло это из-за того, что явная разностная схема является неустойчивой. Неустойчивость выражается в том, что существует некоторое значение шага по времени, при превышении которого погрешность вычислений резко возрастает. Исследование устойчивости выходит за рамки этого изложения, но согласно литературе для данной задачи должно выполняться следующее соотношение:

Как нетрудно проверить, условие не было выполнено. Чтобы удостовериться в работоспособности явной разностной схемы, повторим вычисления для :

для момента времени ; для момента времени для момента времени .

Теперь картина прогревания не противоречит физическому смыслу задачи.

Аналитическое условие устойчивости можно получить только для простых модельных задач, но можно обеспечить устойчивость вычислений алгоритмически в том числе и для нелинейных задач следующим образом:

вычислить значения производных по времени во всех внутренних узлах объекта; определить максимальное из этих значений; разрешить измениться переменной в этом узле на некоторую заданную величину, которая определяется из физического смысла задачи. (Например для нашей задачи максимальной значение температуры внутри стержня , за один шаг по времени можем позволить измениться ей, допустим, на . Исходя из этого вычисляем значение ); выполняем шаг по времени для всех узлов, изменение температуры во всех узлах не превысит разрешенной величины; если модельное время не закончилось переходим к пункту 1.

Рассмотрим решение задачи явной разностной схемой с граничными условиями второго рода (типа Неймана).

Предположим необходимо определить изменение распределения температуры в стержне во времени (изменение температурного поля), теплоизолированном с цилиндрической стороны, с заданной температурой с левой стороны, заданным тепловым потоком с правой (граничные условия) и заданной температурой стержня в нулевой момент времени (начальные условия)(см. рис. 3).

💡 Видео

Решение уравнения теплопроводности методом конечных разностейСкачать

Метод конечных элементов. Основы 1.2.2 - Сборка матриц жесткости. Глобальная матрица жесткостиСкачать

Решение задачи теплопроводности методом конечных разностейСкачать

Основы метода конечных элементов. Часть 3. Основные уравнения теории упругости в МКЭСкачать

Как решать систему уравнений графическим методом? | Математика | TutorOnlineСкачать

Лекция №1.1 Явная и неявная схемы для уравнения теплопроводностиСкачать

РК6. Модели и методы анализа проектных решений. Метод конечных разностей, двумерные задачиСкачать

Сеточные методы решения дифференциальных уравнений в частных производных.Скачать

9 класс, 11 урок, Методы решения систем уравненийСкачать

Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Основы метода конечных элементов. Расчёт элементов фермСкачать

Метод конечных элементов (FEM) vs метод контрольного объёма (FVM). В чём разница?Скачать

Решение уравнения теплопроводности в одномерной постановке в ExcelСкачать

После этого видео, ТЫ РЕШИШЬ ЛЮБУЮ Систему Нелинейных УравненийСкачать

diffurСкачать