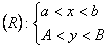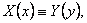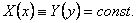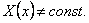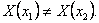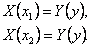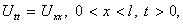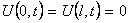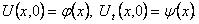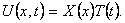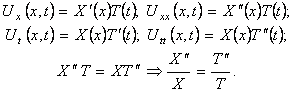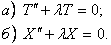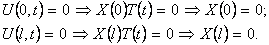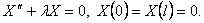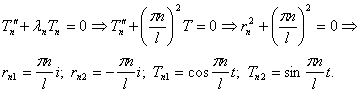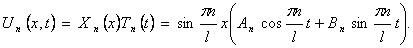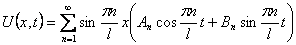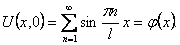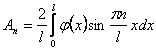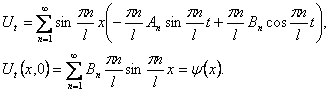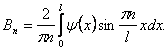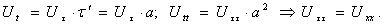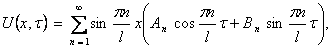Методом фурье решить начально краевую задачу для однородного волнового уравнения

Метод Фурье — один из распространенных и эффективных методов решения уравнений с частными производными. Этот метод часто встречается и под другими названиями: метод разделения переменных или метод собственных функций.

Общая схема метода Фурье.

Основная идея этого метода состоит в том, что решение задачи для уравнения с частными производными сводится к решению вспомогательных задач для уравнений с меньшим числом независимых переменных. В частности, если заданное уравнение содержит две независимые переменные, то вспомогательные задачи будут уже зависеть только от одной переменной. Таким образом решение уравнения с частными производными сводится к решению обыкновенных дифференциальных уравнений.

При применении метода Фурье удобно использовать следующую лемму.

Основная лемма метода Фурье.

Если в прямоугольнике R плоскости XOY:

для некоторых функций выполняется тождество

то в этом случае

Доказательство. Предположим противное, т.е. что

Тогда существуют значения 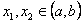такие, что

Рассмотрим точки (x₁,y) и (x₂,y), принадлежащие прямоугольнику R. На R справедливо тождество (8), а поэтому

Сравнивая эти равенства, приходим к противоречию с нашим предположением. Следовательно X(x) = const, а тогда Y(y)=const.

Решение первой начально-краевой задачи для волнового уравнения.

Рассмотрим волновое уравнение

Граничные условия первого рода

И начальные условия

Решим эту задачу методом Фурье.

Шаг 1. Представим функцию U(x,t) в виде

Найдем частные производные U_xx и U_tt и подставим в уравнение (9):

В полученном уравнении левая часть зависит только от x, а правая- только от t. Используя основную лемму, заключаем:

Из граничных условий (10) получим

Шаг 2. Решим задачу Штурма-Лиувилля

Она имеет собственные значения и собственные функции

Шаг 3. Подставим найденные значения λ_n в уравнение а) и решим его:

Шаг 4. Выпишем частные решения уравнения (9):

Для волнового уравнения эти решения называются собственными колебаниями. В лекции 6 мы изучим их подробнее. В силу линейности и однородности уравнения (9) линейная комбинация этих решений

Замечание 1. Здесь мы предполагаем, что полученный функциональный ряд равномерно сходится и его можно дважды почленно дифференцировать по x и по t в области 0 0. Об условиях, при которых это можно сделать, будет рассказано в лекции 5.

Шаг 5. Определим коэффициенты A_nи B_n в формуле (12), используя начальные условия (11). Из первого начального условия получим

Равенство (13) означает, что начальная функция φ(x) разлагается в ряд Фурье по синусам, которые в данном случае являются собственными функциями X_n(x) задачи Штурма-Лиувилля.

Коэффициенты Фурье вычисляются по формулам

Из второго начального условия находятся коэффициенты B_n.

Вычислив коэффициенты A_n и B_n для конкретных начальных функций и подставив их значения в (12), мы получим решение первой начально-краевой задачи.

Замечание 2. Используя формулу (12), можно получить решение первой начально-краевой задачи для уравнения колебания струны: Для этого проведем замену переменной τ=at и получим

При этом начальное условие не изменится, а условие преобразуется к виду Тогда решение задачи в переменных (x,τ) будет иметь вид

Возвращаясь к переменным (x,t), получим

Видео:Метод Фурье для неоднородного уравнения теплопроводностиСкачать

Решение двумерных краевых задач для волнового уравнения методом Фурье

В пп. 5.5 и 5.6 метод Фурье рассмотрен применительно к краевым задачам для волнового уравнения с одной пространственной переменной. Но идею разделения переменных можно распространить и на краевые задачи большей размерности, сформулированные для простых областей, например прямоугольника и круга.

Рассмотрим двумерную первую краевую задачу в прямоугольнике:

Эта задача является, в частности, математической моделью процесса колебаний однородной прямоугольной мембраны (0 2 X(x)Y(y)T(t) получим:

Каждое из отношений из этого равенства зависит только от своей переменной. Поэтому данное равенство возможно для всех значений переменных х, у, t из рассматриваемой области только в случае, когда указанные отношения постоянны, т.е.

С учетом граничных условий (5.86) и (5.87) получаем из (5.90) две задачи Штурма—Лиувилля:

Решения этих задач уже найдены в п. 5.5, см. (5.42), (5.43):

Согласно последнему равенству (5.90) функция T(t) должна удовлетворять уравнению T»(t) + а 2 (к_к + i_n)T(t) = 0 или

Общее решение этого уравнения для различных к, т е N имеет вид

Итак, с учетом (5.89), (5.91), (5.92) и (5.94) можно записать выражение для искомых функций:

которые удовлетворяют уравнению (5.85) и граничным условиям (5.86)—(5.87). Теперь, как и в одномерном случае, следует найти линейную комбинацию этих функций, обеспечивающую выполнение и начальных условий (5.88).

Введем в рассмотрение функции

Нетрудно убедиться, что в прямоугольнике 0 2 (2m -1) 2 1 ..

Перейдем теперь к двумерной краевой задаче для волнового уравнения в другой области простой формы — круге. Рассмотрим математическую модель процесса свободных колебаний однородной мембраны, натянутой на круговой контур радиуса г₀ с центром в начале координат. Будем предполагать, что колебания являются осесимметричными, т.е. в полярных координатах (г, ф) отклонения точек мембраны и(г, ф, /) не зависят от полярного угла ф. Это предположение выполняется для однородной мембраны, если она растянута на круговом контуре симметрично относительно центра круга, а начальные условия осесимметричны.

С учетом формы мембраны для упрощения краевой задачи целесообразно перейти к полярной системе координат. В этой системе оператор Лапласа имеет вид

см. (П2.12). Поскольку и = u(r, t), волновое уравнение в полярной системе координат записывается так:

Граница мембраны закреплена по окружности радиуса г₀, поэтому

Другое граничное условие получим из требования ограниченности функции u(r, t) в особой точке волнового уравнения г = 0:

Начальные условия записываются, как обычно:

Итак, рассматриваемая краевая задача имеет вид

В соответствии с методом Фурье будем искать частные ненулевые решения уравнения (5.101), удовлетворяющие граничным условиям

(5.102), в виде произведения

После подстановки (5.104) в (5.101) и разделения переменных, как и в п. 5.5, получим:

Равенство (5.105) приводит к уравнениям

Если сделать в (5.106) замену переменной г’ = уг, то получим уравнение Бесселя нулевого порядка, см. (П4.3):

Его общее решение

представляется произвольной линейной комбинацией функций Бесселя J₀(r’) и Неймана N₀(r’), см. п. П4.2. Функция N₀(r’) не ограничена при /•’—>+ 0, поэтому согласно второму из граничных условий

(5.102) С₂ = 0, т.е. R(r’) = C_xJ_Q(r’). Положим С_х = 1 и возвратимся к переменной г. Получим частное решение уравнения (5.106), найденное с учетом второго из граничных условий (5.102):

А первое из этих граничных условий приводит к трансцендентному уравнению для значений у:

где р_Л — нули функции Бесселя /₀(х), т.е. /₀(Р/к) = 0. Функция J₀(х) имеет счетное множество нулей: щ = 2,4048; р₂ = 5,5201; р₃ = 8,6537; р₄ = 11,7915; . ; их можно найти в справочной литературе, см., например, [10].

Значениям у_к из (5.108) соответствуют собственные функции

Известно, что система функций |/₀^—г j|, к = 1, 2, . является ортогональной с весом г на отрезке [0; г₀], т.е.

см. п. П4.5. Кроме того, квадрат нормы функции /₀ —г равен

где Ji(x) — функция Бесселя первого порядка, см. формулу (П4.16).

Теперь перейдем к уравнению (5.107). С учетом (5.108) оно принимает вид

а его общее решение

Подставляя выражения (5.109) и (5.110) в (5.104), получим частные решения

уравнения (5.101), удовлетворяющие обоим граничным условиям

(5.102). Остается составить линейную комбинацию этих решений, удовлетворяющую и начальным условиям (5.103):

Коэффициенты А_к и В_к из (5.113) находим с помощью начальных условий (5.103):

Из (5.114) видно, что А_к — это коэффициенты разложения Фурье функции (р(г) по системе |у₀ j j ( см — п — П4.5), т.е. с учетом (5.110)

Из (5.115) аналогично получаем:

Окончательно имеем: искомое решение краевой задачи (5.101)—

(5.103) представляется рядом (5.113) с коэффициентами

Пример 5.7. Найти закон свободных колебаний однородной круглой мембраны радиуса г₀, закрепленной вдоль контура, если начальное распределение отклонений точек мембраны описывается функцией

а начальные скорости точек равны нулю.

Бесселя в самосопряженном виде: (ху’У + х—Iу = 0, см. формулу

(П4.2). Поскольку функция у = /₀(х) есть решение уравнения Бесселя нулевого порядка (v = 0), то

После подстановки левой части (5.119) в (5.118) воспользуемся интегрированием по частям:

(в предпоследнем равенстве использовалось соотношение J’_Q(x) = = -/j(x), см. (П4.10)). Окончательно, искомое решение имеет вид

Видео:Уравнение колебаний струны. Метод разделения переменных. Метод ФурьеСкачать

Решение начально-граничных задач для волнового уравнения методом интегральных преобразований Фурье Текст научной статьи по специальности « Математика»

Видео:Решение первой начально-краевой задачи для волнового уравнения.Скачать

Аннотация научной статьи по математике, автор научной работы — Фахретдинова Дилара Ильдаровна, Сабитова Юлия Камилевна

В данной статье решены начально-граничные задачи для однородного и неоднородного волновых уравнений, методом интегральных преобразований Фурье .

Видео:Неоднородное уравнение колебания струныСкачать

Похожие темы научных работ по математике , автор научной работы — Фахретдинова Дилара Ильдаровна, Сабитова Юлия Камилевна

Видео:Метод Фурье для волнового уравненияСкачать

SOLUTION OF THE INITIAL-BOUNDARY VALUE PROBLEMS FOR THE WAVE EQUATION FOURIER INTEGRAL METHOD

This article addressed the initial-boundary value problems for homogeneous and inhomogeneous wave equation, the Fourier integral method .

Видео:5. Решение волнового уравнения на отрезке методом ФурьеСкачать

Текст научной работы на тему «Решение начально-граничных задач для волнового уравнения методом интегральных преобразований Фурье»

РЕШЕНИЕ НАЧАЛЬНО-ГРАНИЧНЫХ ЗАДАЧ ДЛЯ ВОЛНОВОГО УРАВНЕНИЯ МЕТОДОМ ИНТЕГРАЛЬНЫХ ПРЕОБРАЗОВАНИЙ

Фахретдинова Дилара Ильдаровна

студент 4 курса Стерлитамакского филиала Башкирского Государственного

Университета, РФ, г. Стерлитамак E-mail: dilaragirl09@bk. ru Сабитова Юлия Камилевна канд. физ.-мат. наук, доцент Стерлитамакского филиала Башкирского Государственного Университета, РФ, г. Стерлитамак

SOLUTION OF THE INITIAL-BOUNDARY VALUE PROBLEMS FOR THE WAVE EQUATION FOURIER INTEGRAL METHOD

4th year student of Sterlitamak Branch the Bashkir State University, Russia,

Sterlitamak Julia Sabitova

candidate of physico-mathematical sciences, associate professor of Sterlitamak Branch the Bashkir State University, Russia, Sterlitamak

В данной статье решены начально-граничные задачи для однородного и неоднородного волновых уравнений, методом интегральных преобразований Фурье.

This article addressed the initial-boundary value problems for homogeneous and inhomogeneous wave equation, the Fourier integral method.

Ключевые слова: методом интегральных преобразований Фурье; начально-граничная задача; преобразование Фурье.

Keywords: Fourier integral method; initial-boundary problem; Fourier transform.

Если функция f(x), —го ) 0,

для определения функции йс(Я, £). Решение этой задачи имеет вид

йс(Я, £) = /С(Я) cos(аЯt) + £С(Я)—

Искомую функцию и(х, £) находим с помощью обратного косинус — преобразования Фурье:

📺 Видео

4.3 Решение неоднородного волнового уравнения на бесконечной прямойСкачать

Решение первой краевой задачи для неоднородного уравнения теплопроводности.Скачать

ФОРМУЛА КАРДАНО-ТАРТАЛЬЯ + РЕКЛАМА МФТИ!!!Скачать

Решение первой начально-краевой задачи для одномерного уравнения теплопроводности.Скачать

8.1 Решение уравнения теплопроводности на отрезкеСкачать

10. Волновое уравнение на отрезке. Сложные задачиСкачать

Неоднородное уравнение колебаний струныСкачать

Уравнения математической физики. Одномерное волновое уравнение. Метод Фурье.Скачать

Уравнение колебания струны. Решение методом ДаламбераСкачать

Физика. Лекция 8. Уравнения Максвелла и электромагнитные волны.Скачать

Решение начально-краевых задач в круге для волнового уравнения и теплопроводностиСкачать

Задача Коши для волнового уравнения (Часть 1)Скачать