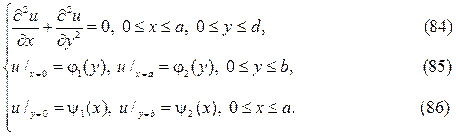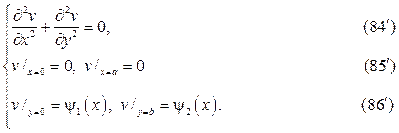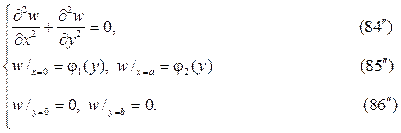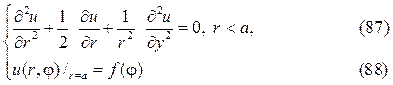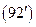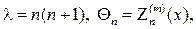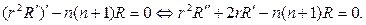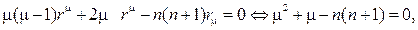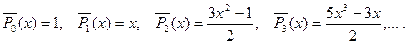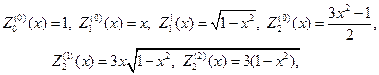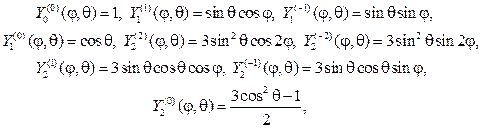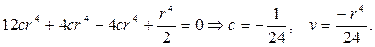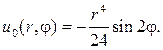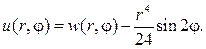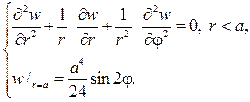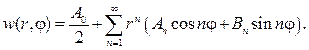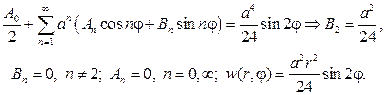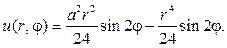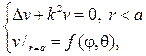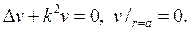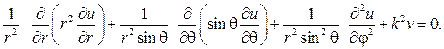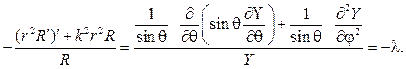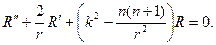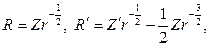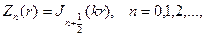Методом фурье решить краевую задачу для уравнения лапласа во внешности круга

По этой ссылке вы найдёте полный курс лекций по математике:

Задача ставится так: найти функцию tx(r,у?), удовлетворяющую внутри ируга Kr0 радиуса с центром в начале координат уравнению Лапласа непрерывную в замжутой области KtQ и принимающую задан ные значения награнице круга, Решение задачи Дирихле для круга методом Фурье где f(tp) — достаточно гладкая функция, периодическая с периодом 2т.

В силу однозначности искомого решения оно должно быть периодическим по с периодом Из непрерывности решения в Кго следует его ограниченность в КГо. Уравнение (1) в полярных координатах имеет вид (3) Будем искать частные решения уравнения (3) в виде . Подставляя «(г, (р) в форме (4) в уравнение (3),умноженное на г2, получим откуда Из условия получаем находим , так что В частности, = Ао = const. Полагая в уравнении (6) (уравнении Эйлера) Л(г) = г*, при А = п2 получаем Отсюда) и, следовательно.

При п = 0 из (6) находам Так как ооприг 0+0,тодля решения внутренней задачи Дирихле нужно положить Решение внутренней задачи Дирихле будем искать в виде ряда (5) (6) где коэффициенты Ап, Вп определяются из граничного условия (2) При т — tq имеем Запишем разложение /(у) в ряд Фурье где Решение задачи Дирихле для круга методом Фурье Сравнивая ряды (8) и (9), получаем (9) * г0 г0.

Таким образом, формальное решение внутренней задачи Дирихле для круга предста-вимо в виде ряда оо где коэффициенты определяются по формулам (10).

Возможно вам будут полезны данные страницы:

При г го ряд (11) можно дифференцировать по г и любое число раз, и, значит, функция u(r, у) из (11) удовлетворяет уравнению Если предположить, что функция непрерывна и дифференцируема, то ряд (11) при г ^ г0 сходится равномерно, и, следовательно, функция и(г, непрерывна на границе круга и удовлетворяет всем условиям поставл енной задачи.

искать в виде ряда где коэффициенты Ап, В„ определяются из граничного условия Для кольцевой области образованной двумя концентрическими окружностями с центром в точке 0 радиусов Г] и г2 (рис.8), решение задачи ищется в виде ряда коэффициенты которого Л0, определяются из граничных условий Пример.

Найти функцию, гармоническую внутри круга радиуса го с центром в начале координат и такую. что Решение задачи Дирихле для круга методом Фурье -4 Задача сводится к решению внутренней задачи Дирихле для уравнения при граничном условии Будем искать решение задачи в вида ряда ПО Из граничного условия (15) имеем Отсюда в силу ортогональности системы функций Искомое решение

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Видео:Уравнение Лапласа. Задача Дирихле для уравнения Лапласа внутри и вне кругаСкачать

МЕТОД РАЗДЕЛЕНИЯ ДЛЯ УРАВНЕНИЙ

ЭЛЛИПТИЧЕСКОГО ТИПА

Краевые задачи для уравнения Лапласа в прямоугольнике (полупо- лосе), решаются методом разделения переменных в декартовых коорди- натах, в круговой областях (круг, сектор, кольцо) методом разделения пе- ременных в полярных координатах. При решении краевых задач для ци-линдрических и сферических областей используются соответственно ци- линдрические и сферические координаты бесселевы функции, полиномы и присоединённые функции Лежандра, а также шаровые функции. Возни- кающие здесь задачи Штурма Лиувилля своеобразны, их граничные ус- ловия определяются спецификой областей:

следует искать в виде суммы u(x,y)=v(x,y)+w(x,y),где v(x,y) и w(x,y) гар- монические функции в том же самом треугольнике, точнее они суть ре-шения краевых задач

Штрихованные краевые задачи решаются методом разделения пере- менных в терминах тригонометрических и гиперболических функций.

Рассмотрим задачу Дирихле для круга

где f(j)кусочно-непрерывная функция.

Следуя схеме метода Фурье полагаем

подставляем в (87) и разделяем переменные. В результате получим ра -венство

(90)

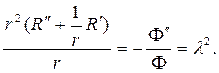
Угловая функция F(j) обязана быть периодической с периодом 2p. Присоединяя условие периодичности к дифференциальному уравнению для F(j), найдем задачу Штурма Лиувилля

откуда следует, что

(91)

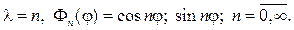
Возвращаясь к (80), решаем уравнение для радианальной функции. При

r 2 R² + rR¢ n 2 R = 0,

решение следует искать в виде степенной функции R=r m . Для определе- ния m получим соотношение

m(m 1)r m +m r m n 2 r m =0Û m 2 n 2 =0,

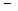
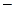
Если же n=0, то уравнение, как нетрудно проверить, rR² + R¢ =0имеет своими решениями функции

R₀(r) = 1; lnr.

С учетом (89) мы должны составить произведения угловых и радиаль- ных функций и получить набор функций, гармонических в круге

Если предположить, что ряд

(93)

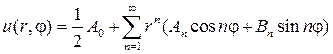
можно дифференцировать почленно дважды по r и j , то его сумма также будет гармонической функцией, т. е. будет решением уравнения (87). Подставляя (93) в (88), найдем

(94)

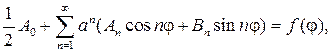
откуда с учетом формул коэффициентов Фурье следует

(95)

(96) Итог состоит в том, что решение задачи (87 88) дается рядом (93), коэффициенты которого определены равенствами (95-96).

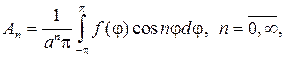
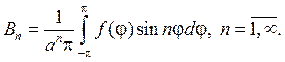
Замечание 1. Мы можем говорить, очевидно, что ряд (93) дает общий вид гармонической функции для круга r — n и lnr, поскольку они разрывны в

центре круга r=0.

Напротив, если рассматривать область r>a, то нельзя привлекать r — n и lnr, и общий вид гармонической функции для внешности круга будет да- ваться рядом

(97)

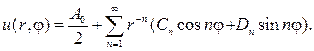
В случае кругового кольца a 2 q= 1-x 2 , найдем

(104¢)

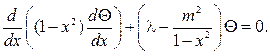
Соответственно и граничные условия (105) перейдут после замены в неравенства

(105′)

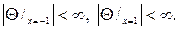
Задача (104¢) (105¢) есть известная задача для присоединенных функций Лежандра, ее решение (см., например, [3], стр. 115)

и возвращаясь к переменной q, найдем собственные значения и собствен- ные функции задачи (104), (105):

(106)

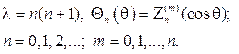
Составив произведения функций (106) на найденные выше функции F_m(j), получим множество решений уравнения (102)

(107)

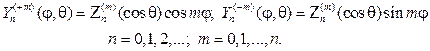
Эти решения принято называть сферическими функциями, их основ-ное свойство в приводимой ниже теореме.

Теорема 1. Сферические функции взаимно ортогональны на единич- ной сфере, т.е. при m₁¹m₂ или n₁¹n₂

(108)

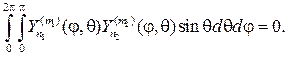
Теперь возвращаясь к равенству (101), возьмем уравнение для ради- альной функции

Оно имеет решение в виде степенной функции R=r m . Действительно, после подстановки

откуда находим значения m=n; (n+1) и соответственно решения

(109)

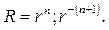
Умножая первые из функций (109) на сферические функции (107), получаем множество частных решений уравнения Лапласа в шаре:

Согласно схеме метода Фурье. составляем ряд с произвольными коэффи- циентами

(110)

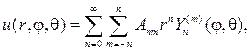
который будет гармонической функцией в шаре, если только его можно дифференцировать почленно.

Для нахождения коэффициентов А_nm подставим (110) в (100), тогда

и с учетом (108) найдем

(111)

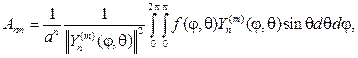
Последний интеграл вычисляется и при m=0 :

(112)

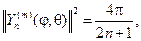
если же |m| ³ 1, то имеем

(113)

Завершая рассмотрение задачи (99),(100), скажем, что мы нашли ее решение в виде ряда (110), коэффициенты которого определяются в согласии с (111),(113).

Замечание 3. Напомним, что нормированные полиномы Лежандра вы- числяяются по формулам

(114)

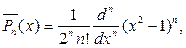
В свою очередь присоединенные функции Лежандра выражаются че- рез производные от полиномов Лежандра, т. е.

(115)

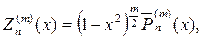
в частности будем иметь

(116)

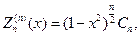
где С_n определенная константа.

С учетом (107), (115) и (116) выпишем несколько сферических функций:

(117)

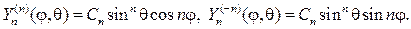
Замечание 4. При решении краевых задач для внешности шара вместо соотношения (110) нужно использовать ряд

(118)

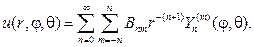
Общий вид гармонической функции в шаровом слое a 4 , и получим

Таким образом, частным решением будет функция

Вводим новую неизвестную функцию w(r,j) , полагая

Тогда относительно w(r,j) нужно решать задачу Дирихле для урав- нения Лапласа

Согласно (93), решение этой задачи дается формулой

Подставляя ее в граничное условие, получим

Ответом в задаче будет функция

254. Найдите решение первой краевой задачи для уравнения Гельмгольца

предполагая, что k не является собственным значением задачи

Р е ш е н и е. Запишем уравнение в сферических координатах

Беря u(r,j,q,)=R(r)Y(j,q), после разделения переменных придем к дифференциальным уравнениям:

Функция 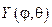будет решением уравнения (72), которое нужно решать при условии ограниченности и 2p-периодичности по j. В результате при- дем к сферическим функциям при l=n(n+1):

Относительно радиальной функции R(r) нужно решать дифференци- альное уравнение

Выполняя в этом уравнении замену

придем к соотношению относительно новой функции Z(r):

Последнее уравнение в качестве ограниченных в окрестности нуля

r=0 решений имеет бесселевы функции

соответственно будем иметь набор радиальных функций

Умножая их на сферические функции, получим набор решений урав- нения Гельмгольца:

Составляем ряд с числовыми коэффициентами

(119)

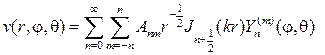
и определяем коэффициенты так, чтобы выполнялась граничное условие при r=a

где d = 4 при m = 0 и d =2 при

При найденных коэффициентах A_nm ряд (119) будет решением рассматриваемой краевой задачи для уравнения Гельмгольца.

255. Найдите такую гармоническую u(r,j,q) функцию внутри шарового слоя 1

Видео:Задача Дирихле для круга. Уравнение ЛапласаСкачать

Методика изложения темы «Решение краевых задач для уравнения Лапласа в прямоугольнике методом Фурье» Текст научной статьи по специальности « Математика»

Видео:6.2 Решение задач для уравнения Лапласа в круге, вне круга и в кольцеСкачать

Аннотация научной статьи по математике, автор научной работы — Попова Елена Михайловна, Чигирёва Ольга Юрьевна

В статье приводится методика изложения темы «Решение краевых задач для уравнения Лапласа в прямоугольнике методом Фурье» в курсе уравнений математической физики в МГТУ им. Н. Э. Баумана. Данный математический аппарат широко используется в физике, математической физике, электродинамике, квантовой механике, акустике, волновой оптике, теории колебаний, теории сигналов и цепей. Цель работы – помочь студентам приобрести навыки применения методов математической физики к решению различных физических задач. Одним из основных методов решения задач математической физики является метод Фурье (разделения переменных). Задача Штурма – Лиувилля – важный этап этого метода. Для того чтобы структурировать основные типы задач Штурма – Лиувилля, в статье приведена таблица, в которой максимально лаконично представлен материал. В работе также кратко приведены основные теоретические сведения и в качестве примера решена краевая задача для уравнения Лапласа в прямоугольнике. Статья будет полезна студентам приборостроительных специальностей, а также преподавателям соответствующих курсов.

Видео:Уравнения математической физики 15+16 Задача Дирихле для уравнения Лапласа - Пуассона в кругеСкачать

Похожие темы научных работ по математике , автор научной работы — Попова Елена Михайловна, Чигирёва Ольга Юрьевна

Видео:Часть 1. Примеры на краевую задачу Лапласа в кругеСкачать

Текст научной работы на тему «Методика изложения темы «Решение краевых задач для уравнения Лапласа в прямоугольнике методом Фурье»»

научно-методический электронный журнал

Попова Е. М., Чигирёва О. Ю. Методика изложения темы «Решение краевых задач для уравнения Лапласа в прямоугольнике методом Фурье» // Научно-методический электронный журнал «Концепт». — 2018. — № У9. — 0,4 п. л. -иН1: http://e-koncept.ru/2018/186085.htm.

ART 186085 УДК 378.147

Попова Елена Михайловна,

кандидат физико-математических наук, доцент ФГБОУ ВО «Московский государственный технический университет им. Н. Э. Баумана», г. Москва elmipo@yandex.ru

Чигирёва Ольга Юрьевна,

кандидат физико-математических наук, доцент ФГБОУ ВО «Московский государственный технический университет им. Н. Э. Баумана», г. Москва m kfn 12@yandex. ru

Методика изложения темы «Решение краевых задач для уравнения Лапласа

в прямоугольнике методом Фурье»

Аннотация. В статье приводится методика изложения темы «Решение краевых задач для уравнения Лапласа в прямоугольнике методом Фурье» в курсе уравнений математической физики в МГТУ им. Н. Э. Баумана. Данный математический аппарат широко используется в физике, математической физике, электродинамике, квантовой механике, акустике, волновой оптике, теории колебаний, теории сигналов и цепей. Цель работы -помочь студентам приобрести навыки применения методов математической физики к решению различных физических задач. Одним из основных методов решения задач математической физики является метод Фурье (разделения переменных). Задача Штурма -Лиувилля — важный этап этого метода. Для того чтобы структурировать основные типы задач Штурма — Лиувилля, в статье приведена таблица, в которой максимально лаконично представлен материал. В работе также кратко приведены основные теоретические сведения и в качестве примера решена краевая задача для уравнения Лапласа в прямоугольнике. Статья будет полезна студентам приборостроительных специальностей, а также преподавателям соответствующих курсов.

Ключевые слова: метод Фурье разделения переменных, задача Штурма — Ли-увилля, уравнение Лапласа.

Раздел: (01) отдельные вопросы сферы образования.

При подготовке студентов приборостроительных специальностей важную роль играет изучение аналитических методов решения задач математической физики [1]. Одним из таких методов является метод Фурье разделения переменных 2, согласно которому решение ищется в виде разложения в ряд Фурье по системе собственных функций задачи Штурма — Лиувилля.

Для успешного освоения студентами данной темы в работе приводятся необходимые теоретические сведения из функционального анализа [5]. Особое внимание уделено рассмотрению задачи Штурма — Лиувилля. Изложенный материал включает постановку задачи, свойства собственных значений и собственных функций [6]. Приведена таблица, в которую сведены наиболее часто встречающиеся типы задач Штурма — Лиувилля для отрезка [7]. Работа содержит краткие теоретические сведения, связанные с постановкой краевых задач для уравнения Лапласа; доказательства сформулированных теорем можно найти в [8, 9]. Показан пример решения краевой задачи для уравнения Лапласа в прямоугольной области.

Структурированный подход к изложению материала, сочетающий основные теоретические сведения и подробно разобранный пример решения краевой задачи, позволяет студентам не только овладеть математическим аппаратом, но и научиться применять его при решении прикладных задач.

1бб11 2эо4-12ох Попова Е. М., Чигирёва О. Ю. Методика изложения темы «Решение краевых задач для уравнения Лапласа в прямоугольнике методом Фурье» // Научно-методический электронный журнал «Концепт». — 2018. — № У9. — 0,4 п. л. -иН1: http://e-koncept.ru/2018/186085.htm.

научно-методический электронный журнал

Для описания стационарных процессов в физике обычно используют уравнения эллиптического типа. Наиболее распространенным уравнением этого типа является уравнение Лапласа

где A — дифференциальный оператор 2-го порядка, называемый оператором Лапласа.

К уравнению Лапласа приводят задачи о стационарном тепловом состоянии однородного тела, равновесном распределении электрических зарядов на поверхности проводника, об установившемся движении несжимаемой жидкости и многие другие.

При решении краевых задач для уравнения Лапласа используют различные аналитические методы: метод Фурье разделения переменных, метод функции Грина и метод интегральных преобразований. В данной работе рассматривается метод Фурье разделения переменных.

Гильбертово пространство l2 ([ a, b]; р)

Линейное пространство, в котором задана норма, называют нормированным пространством.

Нормированное пространство называют полным или банаховым пространством, если в нем любая фундаментальная последовательность сходится.

Гильбертовым пространством называют бесконечномерное банахово пространство, норма в котором индуцирована скалярным произведением

Примером гильбертова пространства является пространство функций, суммируемых с квадратом на отрезке [a,b] с весом р(x) > 0:

jр(x)/2 (x)dx 0, q(x) e С [a, b], q(x) > 0.

Этот оператор называют оператором Штурма — Лиувилля. К области определения D (L) оператора L отнесем множество функций f е С2 (a, b)п С1 [a, b], удовлетворяющих условию L [f ]e L2 [a, b] и однородным граничным условиям

-af ‘(a) + Pf (a) = 0 , af ‘(b) + PJ (b) = 0, где a, P = const > 0, причем a + P > 0, i = 1,2.

Свойства оператора L:

1) (L [f], g) = (f, L [g]), f, g e D (L );

2) (L [f], f )> 0, f e D(L) .

Задача Штурма — Лиувилля

Рассмотрим следующую краевую задачу с однородными граничными условиями на отрезке [a, b]:

L [X(x)] = 1р(x)X(x), a 0; a, P = const > 0, причем a+P> 0, i = 1,2.

Задачу (1), (2) называют задачей Штурма — Лиувилля. Она состоит в нахождении значений 1, при которых уравнение (1) имеет ненулевые решения X (x) из области определения оператора L . Такие значения 1 называют собственными значениями оператора L , а соответствующие им нетривиальные решения X (x) — собственными функциями оператора L.

Свойства собственных значений и собственных функций задачи Штурма — Лиувилля

1. Множество собственных значений «=1 счетно. При этом каждому собственному значению 1п соответствует с точностью до числового множителя только одна собственная функция Xn (x).

2. Все собственные значения неотрицательны: 1п> 0, n е N и . Значение 1 = 0 может быть собственным значением оператора L только при q(x) = 0 и P = P = 0.

3. Собственные функции Xn (x) и Xm (x), отвечающие различным собственным значениям 1п и 1т, ортогональны на отрезке [a,b] с весом р(x), т. е.

issN 2304-i20x Попова Е. М., Чигирёва О. Ю. Методика изложения темы «Решение краевых задач для уравнения Лапласа в прямоугольнике методом Фурье» // Научно-методический электронный журнал «Концепт». — 2018. — № V9. — 0,4 п. л. -URL: http://e-koncept.ru/2018/186085.htm.

научно-методический электронный журнал

Задача 3: ax = Д = 0 Т 2n — 1)J2 Я = ( n ) , n е N; V 21 J

научно-методический электронный журнал

Попова Е. М., Чигирёва О. Ю. Методика изложения темы «Решение краевых задач для уравнения Лапласа в прямоугольнике методом Фурье» // Научно-методический электронный журнал «Концепт». — 2018. — № V9. — 0,4 п. л. -URL: http://e-koncept.ru/2018/186085.htm.

Задача Штурма — Лиувилля

Собственные значения и собственные функции задачи Штурма — Лиувилля

где / (Р), g (Р), И (Р) и у(Р)> 0 (у(Р)^ 0) — функции, заданные на границе Е области О; Я — внешняя нормаль к границе Е.

Если область, в которой поставлена краевая задача, ограничена, то такая задача называется внутренней.

Далее сформулируем основные свойства 1-й и 2-й внутренних краевых задач на плоскости.

1. Решение внутренней задачи Дирихле на плоскости единственно.

2. Внутренняя задача Дирихле на плоскости разрешима при любой непрерывной функции / (Р).

3. Решение внутренней задачи Неймана на плоскости определяется с точностью до произвольной аддитивной постоянной.

4. Внутренняя задача Неймана на плоскости разрешима при любой непрерывной функции g (Р), удовлетворяющей условию

$Я(Р) Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

где /1 (х) = 4и0 — 1 — I, /2 (х) = и би

issn 2304-120X Попова Е. М., Чигирёва О. Ю. Методика изложения темы «Решение краевых задач для уравнения Лапласа в прямоугольнике методом Фурье» // Научно-методический электронный журнал «Концепт». — 2018. — № V9. — 0,4 п. л. -URL: http://e-koncept.ru/2018/186085.htm.

научно-методический электронный журнал

Решение. Согласно методу Фурье, решение u (x, y) краевой задачи (3)-(5) будем искать в следующей форме:

u (x, y ) = X (x) Y (y 0. (6)

Запишем дифференциальный оператор A, стоящий в левой части уравнения

(3), в виде A = ——L , где L =—. Далее подставим предполагаемую форму реше-

ния (6) в уравнение (3):

X ( x ) Y'( y )-Y ( y ) L [ X (x )] = 0. После разделения переменных получим соотношение: L [ X (x)] Y •( y) X (x) = Y (y)» •

В результате уравнение (3) в частных производных «распадается» на два дифференциальных уравнения:

L [ X (x)] = 1X (x), 0 Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

5. Kolmogorov, A. N. & Fomin, S. V. (1972). Jelementy teorii funkcij i funkcional’nogo analiza, Nauka, Moscow (in Russian).

6. Vladimirov, V. S. (1988). Op. cit.

научно-методический электронный журнал

Попова Е. М., Чигирёва О. Ю. Методика изложения темы «Решение краевых задач для уравнения Лапласа в прямоугольнике методом Фурье» // Научно-методический электронный журнал «Концепт». — 2018. — № V9. — 0,4 п. л. -URL: http://e-koncept.ru/2018/186085.htm.

7. Feoktistov, V. V. & Chigirjova, O. Ju. (2015). Uravnenija matematicheskoj fiziki i special’nye funkcii: metod. ukazanija k vypolneniju domashnego zadanija, Izd-vo MGTU im. N. Je. Baumana, Moscow (in Russian).

8. Vladimirov, V. S. (1988). Op. cit.

9. Sveshnikov, A. G., Bogoljubov, A. N. & Kravcov, V. V. (2004). Op. cit.

Рекомендовано к публикации:

Горевым П. М., кандидатом педагогических наук, главным редактором журнала «Концепт»

Поступила в редакцию Received 14.06.18 Получена положительная рецензия Received a positive review 10.07.18

Принята к публикации Accepted for publication 10.07.18 Опубликована Published 30.09.18

Creative Commons Attribution 4.0 International (CC BY 4.0) © Концепт, научно-методический электронный журнал, 2018 © Попова Е. М., Чигирёва О. Ю., 2018

💥 Видео

УМФ, 24.11, уравнение Лапласа в кругеСкачать

OTAROVA JAMILA МЕТОД ФУРЬЕ РЕШЕНИЯ КРАЕВОЙ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА В ПРЯМОУГОЛЬНОЙСкачать

7.2 Уравнение Лапласа в секторе и кольцевом сектореСкачать

Метод Фурье для неоднородного уравнения теплопроводностиСкачать

7.1 Решение уравнения Лапласа в прямоугольникеСкачать

Уравнение колебаний струны. Метод разделения переменных. Метод ФурьеСкачать

Задача Дирихле для уравнения Лапласа в кольце и сектореСкачать

15. Решение уравнения теплопроводности в кругеСкачать

6.1 Уравнение Лапласа в полярных координатах. Принцип решения и постановка задачСкачать

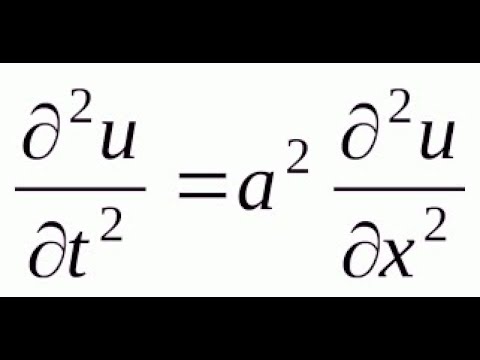
Решение начально-краевых задач в круге для волнового уравнения и теплопроводностиСкачать

Решение уравнения Лапласа в шареСкачать

6.1 Смешанные краевые задачи для уравнений гиперболического и параболического типов. Метод Фурье.Скачать

Колыбасова В.В. - Методы математической физики.Семинары - 14. Уравнение Лапласа в цилиндреСкачать

Решение первой начально-краевой задачи для одномерного уравнения теплопроводности.Скачать

УМФ. Метод Фурье для параболического уравненияСкачать