Проведение аналитического выравнивания предполагает следующую последовательность действий:
- • выбор вида математической функции в качестве модели тренда. Для этих целей анализируют: 1) форму кривой, полученную на основе графического отображения эмпирически данных или данных, сглаженных методом скользящей средней; 2) абсолютные и относительные показатели изменения уровней динамического ряда. Как правило, отбирают не одну, а несколько функций;
- • определение параметров уравнения на основе метода наименьших квадратов по эмпирическим данным;
- • оценка адекватности (качества) уравнения тренда
- • составление прогноза на основе выбранного уравнения тренда.
Выбор вида математической функции
При анализе рядов динамики в качестве модели линии тренда чаще всего используются следующие функции.
Вид математической функции
Условия применения функции
Уровни эмпирического ряда динамики меняются в арифметической прогрессии (цепные абсолютные приросты относительно постоянны).
Парабола 2-ого порядка
Ускоренное или замедленное изменение уровней ряда, когда относительно неизменны вторые разности уровней (цепные абсолютные приросты цепных абсолютных приростов).
Уровни ряда меняются в геометрической прогрессии, т.е. цепные коэффициенты (темпы) роста относительно стабильны.
Г иперболическая а.
Значение уровней ряда во времени уменьшается, постепенно замедляя свою скорость и приближаясь к некоторому пороговому значению, не достигая его
Возможности современного программного обеспечения (например, система STATISTICA, программа Excel) позволяют использовать в качестве модели тренда, кроме указанных выше, более широкий спектр математических функций вплоть до произвольно заданных.
Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Определение параметров уравнения
Для определения параметров уравнения тренда на основе метода наименьших квадратов исходят из условия, что сумма квадратов отклонений фактических уровней ряда динамики от уровней, исчисленных по уравнению тренда, должна быть минимальной:
Для нахождения параметров выбранной математической функции, при которых выполняется это условия, первые частные производные функции (9.30) приравнивают к нулю. В результате получают систему нормальных линейных уравнений.
При выравнивании, например, по линейной функции ее параметры а о и a i находят путем решения следующей системы нормальных линейных уравнений:
Для упрощения расчетов при нахождении параметров уравнения показатель времени удобно обозначить так, чтобы выполнялось равенство = 0. Это достигается, используя следующий прием.
При нечетном количестве уровней ряда моменту (периоду) времени, находящемуся в центре ряда, придается значение t = 0, предыдущим- присваивают значения —1, -2, -3 и т.д., последующим — значения 1, 2, 3 и т.д. (т.е. с шагом 1 от середины ряда в одну и другую сторону от центра).
При четном количестве уровней ряда в середине ряда находятся два момента (периода) времени. Более раннему присваивают значение t = -1, а другому t = +1. Тогда предыдущие моменты времени получают значения -3, -5 и т.д., а последующие значения +3, +5 и т.д., (т.е. с шагом 2 в одну и другую сторону от центра).
При подобном способе обозначения показателя времени система уравнений (9.31) упрощается и принимает следующий вид:
Отсюда параметры линейной функции ао и aj находят следующим образом:
1. Сумма выравненных (теоретических) значений должна равняться сумме эмпирических значений уровней ряда динамики. 2. Принятая система обозначения показателя времени влияет на интерпретацию параметров уравнения тренда. 3. Приводя результаты аналитического выравнивания необходимо указывать принятую систему обозначения показателя времени. 4. При нахождении параметров гиперболы невозможно применение принципа условного обозначения времени, при котором центральному периоду (моменту) времени придается значение t = 0. Поэтому моменты (периоды) времени просто нумеруются, т.е. условному показателю времени присваиваются значения (1, 2, 3 и т.д.) начиная с первого уровня ряда. Проведем аналитическое выравнивание ряда, представленного в табл. 9.14, по линейной функции, поскольку, как легко видеть, цепные абсолютные приросты в этом ряду колеблются незначительно. Инвестиции в основной капитал за 2011-2016 гг. Видео:ОВР и Метод Электронного Баланса — Быстрая Подготовка к ЕГЭ по ХимииСкачать  Методы «аналитического» выравнивания1.2.2 Методы «аналитического» выравнивания Более точным способом отображения тенденции динамического ряда является аналитическое выравнивание, т. е. выравнивание с помощью аналитических формул. В этом случае динамический ряд выражается в виде функции у (t), в которой в качестве основного фактора принимается время t, и изменения аргумента функции определяют расчетные значения уt. Фактическими (или эмпирическими) уровнями ряда динамики называют исходные данные об изменении явления, т. е. данные, полученные опытным путем, посредством наблюдения. Они обозначаются уi. Расчетными (или теоретическими) уровнями ряда называют значения, полученные в результате подстановки в уравнение тренда значений t, и обозначают их. Целью аналитического выравнивания динамического ряда является определение аналитической или графической зависимости f(t) . На практике по имеющемуся временному ряду задают вид и находят параметры функции f(t) , а затем анализируют поведение отклонений от тенденции. Функцию f(t) выбирают таким образом , чтобы она давала содержательное объяснение изучаемого процесса . Чаще всего при выравнивании используются следующий зависимости : линейная параболическая экспоненциальная или 1)Линейная зависимость выбирается в тех случаях , когда в исходном временном ряду наблюдаются более или менее постоянные абсолютные и цепные приросты , не проявляющие тенденции ни к увеличению , ни к снижению. 2)Параболическая зависимость используется , если абсолютные цепные приросты сами по себе обнаруживают некоторую тенденцию развития , но абсолютные цепные приросты абсолютных цепных приростов (разности второго порядка) никакой тенденции развития не проявляют . 3)Экспоненциальные зависимости применяются , если в исходном временном ряду наблюдается либо более или менее постоянный относительный рост (устойчивость цепных темпов роста , темпов прироста , коэффициентов роста) , либо , при отсутствии такого постоянства , — устойчивость в изменении показателей относительного роста (цепных темпов роста цепных же темпов роста , цепных коэффициентов роста цепных же коэффициентов или темпов роста и т.д.) Таким образом, целью аналитического выравнивания является: — определение вида функционального уравнения; — нахождения параметров уравнения; — расчет «теоретических», выровненных уровней, отображающих основную тенденцию ряда динамики. Графическое отображение изменения уровней ряда играет большую роль в применении данного вида выравнивания. Оно позволяет ускорить процедуру анализа и увеличить степень наглядности полученных результатов. Сезонность – изменения динамических рядов, имеющих внутригодичную цикличность, зависящие от календарного периода года, явлениями природы, праздниками и др. Например, объем продаж продукции меховой фабрики вырастет в октябре, в ноябре достигнет максимума, снизится к марту, и затем до сентября — октября будет держаться на очень низком уровне. В качестве примера, интересно сравнить сезонные изменения уровня цен в России и странах Западной Европы. В России уровень цен в предпраздничные дни (например, рождество, Новый год, 9 мая, 1 сентября и т. д.) заметно растет. Тогда как в Западной Европе, как правило, в предпраздничные дни проводятся распродажи, т. е. в большинстве своем цены падают. Явления, подверженные сезонным изменениям, необходимо исследовать на предмет наличия основной тенденции развития. Для этого необходимо распределить объем изменения явления между сезонной составляющей и основной тенденцией. Изучение и измерение сезонности ряда динамики осуществляется с помощью специального показателя – индекса сезонности . Существует несколько вариантов анализа динамики с помощью индекса сезонности. Индексы сезонности показывают , во сколько раз фактический уровень ряда в момент или интервал времени t больше среднего уровня либо уровня , вычисляемого по уравнению тенденции f(t) . При анализе сезонности уровни временного ряда показывают развитие явления по месяцам (кварталам) одного или нескольких лет . Для каждого месяца (квартала) получают обобщенный индекс сезонности как среднюю арифметическую из одноименных индексов каждого года . Индексы сезонности – это , по либо уровень существу , относительные величины координации , когда за базу сравнения принят либо средний уровень ряда , либо уровень тенденции . Способы определения индексов сезонности зависят от наличия или отсутствия основной тенденции . Если тренда нет или он незначителен , то для каждого месяца (квартала) индекс рассчитывается по формуле 32: где
Как отмечалось выше , для обеспечения устойчивости показателей можно взять больший промежуток времени . В этом случае расчет производится по формулам 33 : где При наличии тренда индекс сезонности определяется на основе методов , исключающих влияние тенденции . Порядок расчета следующий : 1) для каждого уровня определяют выравненные значения по тренду f(t); 2) рассчитывают отношения 3) при необходимости находят среднее из этих отношений для одноименных месяцев (кварталов) по формуле :
II. Расчетная часть. 1. Динамика потребления овощей на одного члена домохозяйства в области за 1993-2001 гг. характеризуется следующими данными:
Выявить основную тенденцию потребления овощей на одного члена домохозяйства за 1993 – 2001 гг.: 1) методом сглаживания с помощью 3-членной скользящей средней; 2) методом аналитического выравнивания; 3) постройте график потребления овощей на одного члена домохозяйства области по фактическим и выровненным данным. 1.Выявим тенденцию потребления овощей на одного члена домохозяйства методом сглаживания с помощью трехчленной скользящей средней. Результаты расчетов представив в виде таблицы.
Наблюдается тенденция к росту потребления овощей на одного члена домохозяйства. 2.Выявим основную тенденцию потребления овощей на одного члена домохозяйства методом аналитического выравнивания по уравнению линейного тренда. yt = а0 + а1t ; где а0 и а1 найдем из системы нормальных уравнений. Составим расчетную таблицу.
Отсюда уравнение линейного тренда имеет вид: yt = 3,325t + 24,575 Подставим значения t и запишем расчетные yt в таблицу. Наблюдается тенденция к росту потребления овощей на одного члена домохозяйства. 3.Нанесем на график фактические и выровненные данные. 2. Динамика добычи нефти в республике за отчетный год характеризуется данными:
Определите добычу нефти за каждый квартал и постройте ряд динамики. Для анализа ряда динамики добычи нефти исчислите: Видео:Аналитическое выравниваниеСкачать  АНАЛИТИЧЕСКОЕ ВЫРАВНИВАНИЕАналитическое выравнивание, или выравнивание уровней ряда по аналитическим формулам, — более достоверный и точный метод обработки рядов динамики, позволяющий устранить случайные колебания и выявить основную тенденцию (тренд), поскольку позволяет выразить общую тенденцию изменения уровней в виде математической модели. Сущность данного метода состоит в замене эмпирических (фактических) уровней yj теоретическими у<, которые рассчитываются по выбранному уравнению, принимаемому за математическую модель тренда, где теоретические уровни рассматриваются как функция времени у, =/(/). В аналитическом выравнивании могут использоваться следующие виды уравнений:
Выбор той или иной функции для выравнивания ряда динамики производится, как правило, на основании анализа характера закономерности динамики данного явления, а также графического изображения исходных (фактических) данных. Параметры искомых уравнений при аналитическом выравнивании определяют, как правило, решая систему нормальных уравнений, полученных методом наименьших квадратов (возможны и другие приемы). Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать  Метод наименьших квадратовСуть МНК в следующем требовании: расчетные значения у( должны обеспечивать минимальную сумму квадратов их отклонений от фактических значений: (минимизируются именно квадраты отклонений, поскольку по свойству арифметической средней (у, — у,) 2 = 0). При постановке данного условия становится возможным определить, при каких значениях о0, а, и т.д. для каждой аналитической кривой сумма квадратов отклонений будет минимальной. Аппроксимация (от лат. approxima — приближаюсь) — замена одних математических объектов другими, более простыми и в том или ином смысле близкими к исходным. Выравнивание по прямой (по линейной функции)^ = а0 + я,t. В соответствии с требованием МНК вместо yt подставляем его конкретное выражение а0 + a <t. Далее решается задача на экстремум, т.е. определяется, при каком значении а0 и а< функция двух переменных /’может достигнуть минимума. Далее находят частные производные Fno aQ и av приравнивают их к нулю и после дальнейших преобразований решают систему двух уравнений с двумя неизвестными. В соответствии с изложенным определяют частные производные: Сократив каждое уравнение на -2, раскрыв скобки и перенеся члены в одну сторону, а у — в другую, получим где п — количество уровней ряда; t — порядковый номер в условном обозначении периода или момента времени; у — уровни эмпирического (фактического) ряда. Решение данной системы возможно несколькими способами, в результате чего получают следующие формулы для а0и а< Таким образом, для каждого вида теоретической кривой рассчитывается своя система нормальных уравнений. Пример 10.4. Рассмотрим на примере данные о единовременной вместимости гостиниц и аналогичных средств размещения за 2009— 2013 гг. (табл. 10.7, графы 1, 2), тыс. мест. Расчетная таблица для определения уравнения тренда Единовременная вместимость гостиниц и иных средств размещения, тыс. мест, 🎥 Видео11. Прямая в пространстве и ее уравненияСкачать  1 Решение задачи графическим и аналитическим методомСкачать  Решение ОВР методом полуреакцийСкачать  ЭТОТ метод поможет на уроках ХИМИИ / Химия 9 классСкачать  Как решать уравнения по схеме ГорнераСкачать  Аналитическая геометрия, 6 урок, Уравнение прямойСкачать  Урок 1. Матрицы, определитель матрицы и ранг матрицы | Высшая математика | TutorOnlineСкачать  Разложение по элементам двух строк Определитель 5 порядкаСкачать  Индивидуальный проект: как отражаем в ООП СОО и в аттестате? 23.01.2024 Ссылки на видео нижеСкачать  Аналитическая геометрия, 8 урок, Поверхности второго порядкаСкачать  Формула Муавра ➜ Вычислить ➜ (5+5i)⁷Скачать  МЕТОД АЛГЕБРАИЧЕСКОГО СЛОЖЕНИЯ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ II #математика #егэ #shorts #профильныйегэСкачать  СИСТЕМЫ УРАВНЕНИЙ В ЕГЭ ЧАСТЬ I #shorts #математика #егэ #огэ #профильныйегэСкачать  LXtalks#34 Соня Смыслова о трансформации образования, развитии методистов и креативных профессияхСкачать  Щелчок по математике I №9 Текстовые задачи всех видовСкачать  |




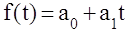 ;
;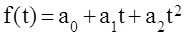 ;
;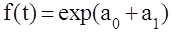
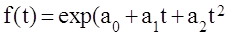 ).
).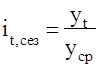
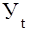 — уровень показателя за месяц (квартал) t ;
— уровень показателя за месяц (квартал) t ;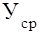 — общий уровень показателя .
— общий уровень показателя .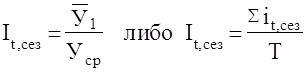
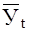 — средний уровень показателя по одноименным месяцам за ряд лет ;
— средний уровень показателя по одноименным месяцам за ряд лет ;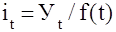 ;
;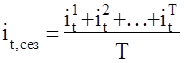 ,(Т — число лет).
,(Т — число лет).




