Методика изучения тригонометрических уравнений и неравенств в 10 11 классах средней школы

Курс математики корпорации «Российский учебник», авторства Георгия Муравина и Ольги Муравиной, предусматривает постепенный переход к решению тригонометрических уравнений и неравенств в 10 классе, а также продолжение их изучения в 11 классе. Представляем вашему вниманию этапы перехода к теме с выдержками из учебника «Алгебра и начало математического анализа» (углубленный уровень).

1. Синус и косинус любого угла (пропедевтика к изучению тригонометрических уравнений)

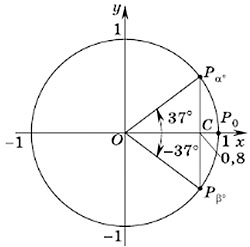
Пример задания. Найти приближенно углы, косинусы которых равны 0,8.

Решение. Косинус — это абсцисса соответствующей точки единичной окружности. Все точки с абсциссами, равными 0,8, принадлежат прямой, параллельной оси ординат и проходящей через точку C(0,8; 0). Эта прямая пересекает единичную окружность в двух точках: P_α° и P_β°, симметричных относительно оси абсцисс.

С помощью транспортира находим, что угол α° приближенно равен 37°. Значит, общий вид углов поворота с конечной точкой P_α°:

α° ≈ 37° + 360°n, где n — любое целое число.

В силу симметрии относительно оси абсцисс точка P_β° — конечная точка поворота на угол –37°. Значит, для нее общий вид углов поворота:

β° ≈ –37° + 360°n, где n — любое целое число.

Ответ: 37° + 360°n, –37° + 360°n, где n— любое целое число.

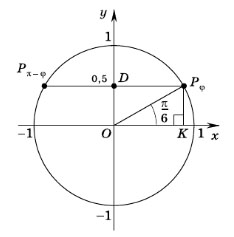
Пример задания. Найти углы, синусы которых равны 0,5.

Решение. Синус — это ордината соответствующей точки единичной окружности. Все точки с ординатами, равными 0,5, принадлежат прямой, параллельной оси абсцисс и проходящей через точку D(0; 0,5).

Эта прямая пересекает единичную окружность в двух точках: P_φ и P_π–φ, симметричных относительно оси ординат. В прямоугольном треугольнике OKP_φ катет KP_φ равен половине гипотенузы OPφ, значит,

Общий вид углов поворота с конечной точкой P_φ:

где n — любое целое число. Общий вид углов поворота с конечной точкой P_π–φ:

где n — любое целое число.

Ответ: где n — любое целое число.

2. Тангенс и котангенс любого угла (пропедевтика к изучению тригонометрических уравнений)

Пример 2. Найти общий вид углов, тангенс которых равен –1,2.

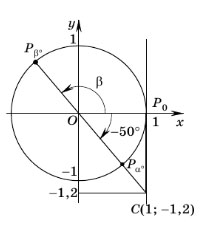
Пример задания. Найти общий вид углов, тангенс которых равен –1,2.

Решение. Отметим на оси тангенсов точку C с ординатой, равной –1,2, и проведем прямую OC. Прямая OC пересекает единичную окружность в точках P_α° и P_β° — концах одного и того же диаметра. Углы, соответствующие этим точкам, отличаются друг от друга на целое число полуоборотов, т.е. на 180°n (n — целое число). С помощью транспортира находим, что угол P_α° OP₀ равен –50°. Значит, общий вид углов, тангенс которых равен –1,2, следующий: –50° + 180°n (n — целое число)

По синусу и косинусу углов 30°, 45° и 60° легко найти их тангенсы и котангенсы. Например,

Перечисленные углы довольно часто встречаются в разных задачах, поэтому полезно запомнить значения тангенса и котангенса этих углов.

Видео:РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ😉 #shorts #егэ #огэ #математика #профильныйегэСкачать

Тригонометрические уравнения и неравенства в содержании школьных учебников по алгебре и началам математического анализа

Тригонометрические уравнения и неравенства изучаются в 10-11 классах в рамках 102 — часового курса «Алгебра и начала математического анализа.

Просмотр содержимого документа
«Тригонометрические уравнения и неравенства в содержании школьных учебников по алгебре и началам математического анализа»

Тригонометрические уравнения и неравенства в содержании школьных учебников по алгебре и началам математического анализа

В настоящее время вопросы решения тригонометрических уравнений и неравенств изучаются в 10-11 классах в рамках 102 — часового курса «Алгебра и начала математического анализа».

Проанализируем различные учебники курса алгебры и начал математического анализа последних лет, чтобы выяснить, каким образом идет изложение темы «Тригонометрические уравнения и неравенства».

В качестве таких учебников мы рассмотрим следующие:

Алгебра и начала математического анализа. 10-11 классы. Учебник. (базовый уровень) Алимов А.Ш., Колягин Ю.М. и др. — М.: Просвещение, 2012 [8].

Алгебра и начала анализа. Учебник для 10 – 11 кл. средн. шк. / М. И. Башмаков. – М.: Просвещение, 2010 [3].

Алгебра и начала математический анализ. 10 кл. Углубленный уровень/ Н.Я.Виленкин, О.С.Ивашев-Мусатов, С. И. Шварцбурд. – М., 2014 [4].

Алгебра и начала математического анализа. Учебник для 10-11 кл./ А.Н. Колмогоров, О.С. Ивашев-Мусатов, Б.М. Ивлев, С.И. Шварцбурд, – М.: Просвещение, 2008 [9].

Алгебра и начала математического анализа. 10-11 кл. В 2 ч. Ч. 1. Учебник (базовый уровень) / А.Г.Мордкович. – М., 2013 [7].

Алгебра и начала математического анализа. 10 кл. В 2 ч. Ч. 1. Учебник (проф. уровень) / А. Г. Мордкович, П. В. Семенов. – М. 2009 [5].

Алгебра и начала математического анализа. 10 класс. Учебник: базовый и проф. уровни / С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин. – М.: Просвещение, 2009 [6].

Прежде всего, отметим некоторые особенности этих учебников в целом. Данные учебники дают цельное и полное представление о школьном курсе алгебры и начала анализа, отвечают требованиям обязательного минимума содержания образования. Но каждый из них имеет свои особенности.

Учебник [7], например, отличается более доступным для школьников, по сравнению с остальными учебниками, изложением теоретического материала, которое ведется очень подробно, обстоятельно и достаточно живым литературным языком, наличием большого числа примеров с подробными решениями. Построение всего курса осуществляется на основе приоритетности функционально-графической линии.

Учебник [9] имеет прикладную направленность, содержание отличается большей научностью и близостью к математическому анализу, язык изложения в большей мере научен, чем доступен. Теоретический материал изложен достаточно кратко и лаконично.

Учебник [3] также имеет прикладную направленность, но в отличие от [9] ориентирован на физические приложения математических знаний и умений. В конце учебника представлены несколько лабораторных работ. В конце учебника весь изученный материал представлен в виде схем и таблиц, что удобно не только ученику при подготовке к какому-либо контрольному мероприятию, но и учителю при подготовке к уроку или к системе уроков. Также среди достоинств этого учебника стоит отметить и тот факт, что каждая глава открывается вводной беседой, подготавливающей появление новых основных понятий, и заключительной беседой, которая включает в себя сведения, полезные для учащихся, интересующихся математикой.

Учебники [4], [6], предназначенные для изучения курса алгебры и начал анализа в 10-11 классах с профильной подготовкой по математике. Изложение материала в учебнике [4] дается подробно и обстоятельно. Представлены подробные решения большого числа примеров. Отличительной особенностью, как и в [7], является приоритет функционально-графической линии.

В учебнике [6] содержится большое количество образцов решения задач по всем темам, что позволяет достичь результатов в решении задач на базовом уровне. Учебник завершается разделом «Задания для повторения», содержащим задачи как для текущего повторения, так и для подготовки к итоговой аттестации.

Перейдем к анализу изложения непосредственно темы «Тригонометрические уравнения и неравенства» в данных учебниках.

Начнем анализ с учебника [9]. Этот учебник долгие годы был единственным, а затем основным в школе при изучении курса алгебры и начал анализа.

Первое. Отметим последовательность рассмотрения материала. Вначале изучаются тождественные преобразования тригонометрических выражений, далее вопросы, связанные со свойствами функций, в том числе тригонометрических функций. Завершалось изложение решением тригонометрических уравнений и неравенств.

Этот блок материала состоит из следующих вопросов:

решение тригонометрических уравнений;

решение тригонометрических неравенств;

примеры решения тригонометрических уравнений и систем уравнений.

В последнем пункте приводятся примеры уравнений, решаемых с помощью введения новой переменной:

,

,

,

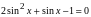
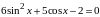
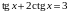
однородные и неоднородные тригонометрические уравнения 2 степени:

,

,

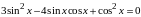
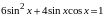
уравнения, решаемые с помощью метода разложения на множители:

,

.

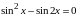
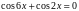
А также рассматривается система

Среди упражнений для решения по отработке материала, помимо аналогичных приведенным, предлагаются однородные уравнения 1 степени и уравнения, которые решаются с помощью применения различных преобразований (ниже мы отнесем их к уравнениям 7 типа).

Отметим еще, что в рассматриваемом учебнике тригонометрические неравенства решаются с привлечением числовой окружности, а учебнике с более ранней версией издания с помощью графиков тригонометрических функций.

В учебнике [8] опять же вначале изучают тождественные преобразования тригонометрических выражений. Далее рассматриваются тригонометрические уравнения и неравенства, а уже затем тригонометрические функции.

Параграф «Решение тригонометрических уравнений» содержит следующие пункты:

уравнения, сводимые к квадратам (отметим, что материал полностью идентичен, как и в учебнике [9]);

уравнения вида .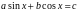

Здесь разбираются задачи:

,

,

».

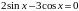
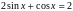
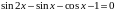
Как видим, в данном учебнике рассматриваются однородные уравнения 1 степени, неоднородные уравнения 1 степени и уравнения, относимые нами далее к 6 типу.

уравнения, решаемые разложением левой части на множители.

Отметим, что в этом пункте помимо заданий, аналогичных как в учебнике [9], предлагаются и такие:

,

».

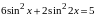
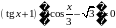
Первое из них предполагает по сравнению со многими другими примерами достаточно нетривиальные преобразования, а второе требует привлечения очень важного утверждения о равенстве произведения нулю, при использовании которого учащиеся очень часто допускают ошибки.

Далее идет параграф о решении простейших неравенств. В этом учебнике они решаются с привлечением числовой окружности.

Отметим также, что задачный материал, предлагаемый в учебнике [8] значительно более богатый, чем в учебнике [9] как с количественной позиции, так и качественной. Самое главное, что есть много заданий, при решении которых требуется активно применять различные формулы тригонометрии (7 тип).

В учебнике [3] изложение материала ведется в последовательности тригонометрические функции  тождественные преобразования тригонометрических выражений  тригонометрические уравнения. В последнем параграфе рассматривают:

1) простейшие тригонометрические уравнения;

2) уравнения, сводимые к алгебраическим, в частности, здесь разбирается неоднородное тригонометрическое уравнение 1 степени, которое решается с помощью универсальной тригонометрической подстановки

;

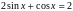
3) уравнения, решаемые понижением степени (7 тип)

,

;

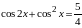
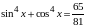
4) уравнения, решаемые после преобразований с помощью тригонометрических формул (7 тип)

,

;

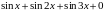
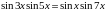
5) однородные и неоднородные тригонометрические уравнения 2 степени.

Тригонометрические неравенства в данном учебнике не рассматриваются.

Упражнения для самостоятельного решения предлагаются в полном соответствие с указанными выше типами уравнений.

В учебнике [7] раздел, связанный с тригонометрией, излагается в такой последовательности: тригонометрические функции  тригонометрические уравнения  тождественные преобразования тригонометрических выражений (с решением соответствующих уравнений и неравенств).

В этом учебнике, как мы видим, раздел материала, касающийся тригонометрических уравнений и неравенств, рассматривается в 2 блоках. В первом из них решение проводится без использования основных формул тригонометрии, во втором уже с их привлечением.

Рассмотрим, какие уравнения рассматриваются в первом блоке. Это:

1) простейшие тригонометрические уравнения и неравенства;

2) однородные тригонометрические уравнения первой и второй степени;

3) неоднородные уравнения 2 степени.

Здесь же значительное место отводится решению заданий с отбором корней. Выделяются два основных метода решения тригонометрических уравнений: введение новой переменной и разложение на множители. В последнем случае предлагается пример

.

Во втором блоке по мере изучения необходимых формул предлагаются соответствующие уравнения и неравенства. Отметим, что в явном виде изучается формула дополнительного аргумента

.

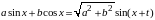
В учебнике [5] для профильного уровня в первом блоке добавляются примеры, которые иллюстрируют наиболее «тонкие» ситуации при решении соответствующих типов уравнений. Например, рассматривается такой пример

,

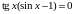
при решении которого требуется учитывать ограничения на переменную.

Во втором блоке в данном учебнике вопрос о решении тригонометрических уравнений уже выделяется в отдельный параграф «Методы решения тригонометрических уравнений». Здесь рассматривается применение формул универсальной тригонометрической подстановки, а также задания повышенного и высокого уровня сложности.

В учебнике [4], изначально рассчитанного на классы математической специализации, тема в целом излагается в классической последовательности: тригонометрические функции  тождественные преобразования тригонометрических выражений  тригонометрические уравнения.

В последнем случае рассматриваются:

1) простейшие тригонометрические уравнения;

2) уравнения, сводимые к простейшим

,

;

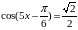
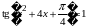
3) уравнения вида

4) уравнения, решаемые методами замены переменной и разложения на множители;

5) различные виды тригонометрических уравнений, при решении которых используются разнообразные формулы тригонометрии (7 тип);

6) простейшие тригонометрические неравенства и неравенства более сложного вида, например,

В учебнике [6], который стал сейчас очень распространенным в профильных классах в нашем городе, материал рассматривается в последовательности тождественные преобразования тригонометрических выражений  тригонометрические функции  тригонометрические уравнения и неравенства.

В теме «Тригонометрические уравнения и неравенства» рассматриваются:

1) простейшие тригонометрические уравнения;

2) уравнения, сводимые к простейшим путем замены переменной

3) уравнения, решаемые с помощью различных формул тригонометрии (7 тип);

5) однородные уравнения, причем n-ой степени;

6) простейшие тригонометрические неравенства и сводимые к ним;

7) уравнения и неравенства, решаемые с помощью формулы дополнительного аргумента;

8) уравнения и неравенства, решаемые заменой

Последние три пункта отмечены звездочкой и рассчитаны на изучение только в профильных классах. Должное внимание уделяется заданиям с отбором корней.

Во всех учебниках, кроме [7], тригонометрические уравнения рассматриваются после изучения формул тригонометрии.

Только в учебниках [7] и [6] уделяется достаточное внимание решению тригонометрических уравнений с отбором корней.

Несмотря на схожесть во многих позициях у авторов в вопросе классификации тригонометрических уравнений, ни в одном учебнике в явном виде такой классификации не проводится, а в ряде случаев одни и те же задания могут быть отнесены в разные типы.

Наиболее полно рассмотрение различных типов тригонометрических уравнений представлено в учебнике [6].

Тригонометрические неравенства в достаточном объеме для профильного уровня рассматриваются в учебнике [4] и [6].

Для разработки эффективной методики изучения тригонометрических уравнений и неравенств необходимо также представлять характер и уровень сложности заданий, которые могут быть предложены учащимся в рамках единого государственного экзамена. Данный анализ мы проводим в третьем параграфе данный главы.

Видео:10 класс, 23 урок, Методы решения тригонометрических уравненийСкачать

Методическая разработка раздела образовательной программы по алгебре «Тригонометрические уравнения» 10 класс
методическая разработка (10 класс) на тему

Видео:10 класс, 22 урок, Простейшие тригонометрические уравнения неравенстваСкачать

Методическая разработка раздела образовательной программы по алгебре «Тригонометрические уравнения» 10 класс

Видео:Методы решения тригонометрических уравнений и неравенствСкачать

Скачать:

Видео:Как решать тригонометрические неравенства?Скачать

Предварительный просмотр:

МБ ОУ Починковская СОШ

программы по алгебре «Тригонометрические уравнения»

Выполнила учитель математики

I квалификационной категории

Данилова Елена Николаевна

1. Психолого-педагогическое объяснение специфики воспитания и освоения учебного материала обучающимися в соответствии с возрастными особенностями.

1. Ожидаемые результаты освоения раздела программы.

1. Образовательные технологии, методы, формы организации деятельности обучающихся.

1. Календарно-тематическое планирование по разделу.

1. Система знаний и система деятельности.

1. Список литературы и адреса образовательных сайтов, используемых при изучении раздела.

В древности тригонометрия возникла в связи с потребностями астрономии, землемерия и строительного дела, то есть носила чисто геометрический характер и представляла главным образом >. Само название «тригонометрия» греческого происхождения, обозначающее «измерение треугольников»: (тригонон) — треугольник, (метрейн) – измерение. Тригонометрия является одним из наиболее молодых отделов элементарной математики, получивших окончательное оформление лишь в XVIII в., хотя отдельные идеи её относятся к глубокой древности, к античному миру и к математическому творчеству индусов (К. Птолемей, II в., Аль Баттани, IX в., и др.).

Образовательный стандарт среднего (полного) общего образования по математике в требованиях к уровню подготовки к выпускнику предусматривает умение решать простейшие тригонометрические уравнения. Но тема «Решение тригонометрических уравнений» входит в материалы итоговой аттестации за курс полной средней школы, в заданиях ЕГЭ.

Практика показывает, что решение тригонометрических уравнений вызывает у учащихся затруднения. После школьной жизни реальной необходимостью в наши дни становится непрерывное образование, что требует полноценной базовой общеобразовательной подготовки, в том числе и математической. И наконец, всё больше специальностей, требующих высокого уровня образования, связано с непосредственным применением математики (экономика, физика, химия, техника, информатика и многое другое). Таким образом, расширяется круг школьников, для которых математика становится профессионально значимым предметом.

Данная методическая разработка предназначена для повышения эффективности подготовки учащихся 10-11-х классов к ЕГЭ за курс полной средней школы и предусматривает их подготовку к дальнейшему математическому образованию. Анализ сдачи единого государственного экзамена показал, что ученики допускают много ошибок при выполнении заданий именно этого раздела или вообще не берутся за такие задания. Одной из причин этого является недостаточное количество программных часов, отводимое на изучение этого раздела, а так же поверхностное изложение некоторых важных вопросов, связанных с решением тригонометрических уравнений, отбором и исследованием корней, решением тригонометрических неравенств.

При разработке раздела программы я использовала учебник «Алгебра и начала анализа» под редакцией А.Г.Мордковича: в качестве основной содержательно-методической линии при изучении тригонометрических уравнений выбрана функционально-графическая линия. Построение материала осуществляется по схеме: функция – уравнения – преобразования.

Ранее в учебниках под редакцией Алимова в течении многих лет тригонометрические уравнения изучались после того, как изучены основные формулы тригонометрии. Почему удобнее сначала изучать функции? Разумнее сначала изучить «чистые» модели функции, а затем учиться работать с «навороченными» моделями. В тригонометрических уравнениях сначала следует разобраться с простейшими тригонометрическими уравнениями и уравнениями, которые сводятся к простейшим с помощью алгебраических приемов без формул тригонометрии (используется лишь основное тригонометрическое тождество si х+ х=1, эта формула следует из уравнения числовой окружности. + =1 и определение синуса и косинуса.) и потом переходить уравнениям, которые необходимо долго и упорно «раскручивать».

Специфика простейших тригонометрических уравнений состоит: Во-первых, в том, что практически никогда до этого учащиеся не сталкивались с ситуацией, чтобы в уравнении было не конечное, а бесконечное множество корней; нужно дать им время, чтобы это понять, осознать и принять. Во-вторых, никогда до сих пор структура записи корней уравнения не выглядела столь сложно и громоздко. Самое трудное, что было до сих пор, – формула корней квадратного уравнения. Теперь же они сталкиваются с записью х = (-1 arcsin m+ , где каждый компонент (и пресловутые «арки», и наличие параметра, и странный «хвост» , и «выкрутасы» типа (-1 ) требует специального осмысления и отработки, для чего нужна соответствующая система упражнений.

Учение о тригонометрических функциях имеет широкое применение в практике, при изучении множества физических процессов, в промышленности, и даже в медицине. Учащиеся, которые в дальнейшем в своей профессиональной деятельности будут пользоваться математикой, необходимо обеспечить высокой математической подготовкой.

2.Цели и задачи раздела.

1. сформировать у учащихся понимание необходимости знаний алгоритмов решения тригонометрических уравнений для дальнейшего изучения тригонометрических неравенств и систем уравнений, при решении задач по геометрии, физике, астрономии;
2. способствовать интеллектуальному развитию учащихся, формированию математического стиля мышления при решении элементарных тригонометрических уравнений, которые необходимы при решении более сложных типов тригонометрических уравнений;
3. формировать представления о решениях тригонометрических уравнений, как составной части решения тригонометрических неравенств, систем уравнений;
4. способствовать повышению уровня самостоятельности учащихся при работе с учебным материалом, развивать точную, информативную речь, формировать умение обосновывать свою точку зрения.

1. акцентировать внимание учащихся на единых требованиях к правилам оформления различных видов заданий, включаемых в ЕГЭ;
2. формировать навыки применения свойств тригонометрических функций и соотношение между тригонометрическими функциями, при решении тригонометрических уравнений и при решении нестандартных задач;
3. развивать способности учащихся к математической деятельности;
4. способствовать совершенствованию и развитию важнейших математических знаний и умений, предусмотренных программой.

3.Психолого-педагогическое объяснение специфики воспитания и освоения учебного материала обучающимися в соответствии с возрастными особенностями.

В старшем школьном возрасте, учащиеся включаются в новый тип ведущей деятельности – учебно-профессиональной. Учебная деятельность становится средством реализации жизненных планов будущего, а основным внутренним мотивом для большинства учащихся является ориентация на результат. Для этой возрастной группы характерным является заметное повышение интереса к учению. Учение приобретает для них непосредственно жизненный смысл в связи с осознанием знаний и умений как необходимого условия достойного участия в будущей жизни. Учебная деятельность старшеклассников включает элементы анализа, исследования, личностного самоопределения. Избирательность интересов связана с жизненными планами. Старшие школьники могут интересоваться двумя-тремя профилирующими по отношению к будущей профессии предметами при равнодушии и безразличии к остальным. Изменяется мотивация в основных видах деятельности: учения, общения, труда. На месте прежних (детских) мотивов возникают и закрепляются новые (взрослые) мотивы, приводящие к переосмыслению содержания, целей и задач деятельности.

Как и на других уроках на уроке математики старшеклассника отличает активность мышления, направленность на решение мыслительных задач, вкус к логическому упорядочиванию и систематизации, к поиску универсальных закономерностей, к самостоятельному нахождению способов обобщенной ориентировки в материале, с теоретическим обобщением. Самостоятельная деятельность учащихся очень важный фактор формирования познавательного интереса. Но иногда надо дать стимул для самостоятельного изучения какого-либо явления, так как, изучая его, разбираясь в его проблемах и связями с жизнью, у ученика возникнет неподдельный интерес к изучаемому процессу. Эти самостоятельные задания надо предлагать с учетом склонностей учеников, чтобы это не была работа ради галочки у учителя в тетради. Задав однажды какую-либо тему для исследования, надо в дальнейшем задавать, либо тему в развитии данной проблемы, либо тему в смежной области к области приложения исследования, то есть не давать единичных заданий, которые могут разбудить интерес лишь на время. Но и нельзя изучение проблемы полностью возлагать на плечи ученика, так как это может дать обратный эффект (это уже элемент приневоливания). Надо уловить заинтересовала ли заданная тема ученика или он просто сделал очередное задание.

4.Ожидаемые результаты освоения

В результате изучения раздела «Тригонометрические уравнения» обучающие должны:

1) решать уравнения вида: sin x=a, cos x=a, tg x=a и знать решение их частных случаев;

2) знать различные приёмы решения линейных, квадратных уравнений и уравнений, сводящихся к ним;

3) применять графический метод для решения уравнений, для определения принадлежности корней рассматриваемому промежутку, отбора корней;

4) владеть системой функциональных понятий, знать тригонометрические функции, предусмотренные минимумом содержания обучения, их свойств и графиков;

5) применять обратные тригонометрические функции для проверки полученных решений уравнений.

6) овладеть стилем мышления, характерным для математика, его доказательностью, строгостью;

7) уметь логически обосновывать ход преобразований, применять различные способы решения уравнений и уметь выдвигать гипотезы в решении уравнений;

8) уметь ясно, точно и грамотно выражать свои мысли в устной и письменной речи, использовать графический язык математики и свободно переходить от алгебраического метода решения уравнений к графическому методу;

9) уметь использовать разнообразные информационные источники для подготовки к занятию;

10) уметь осуществлять алгоритмическую деятельность и конструировать новые умения для решения более сложных задач.

11) понимать, что решение тригонометрических уравнений является неотъемлемой частью раздела «Тригонометрия», её знание необходимо для решения тригонометрических неравенств и систем уравнений;

12) понимать, что решение тригонометрических уравнений возникло из потребностей человеческой практики и продолжает развиваться;

13) понимать, что математическая символика и формулы тригонометрии позволяют описывать общие свойства решения не только тригонометрических уравнений, но и систем уравнений, неравенств не только в алгебре, но и в геометрии, физике и астрономии.

5.Образовательные технологии, методы, формы организации деятельности обучающихся.

В современном обществе смысл и значение образования меняются. Теперь это не просто усвоение знаний, а импульс к развитию способностей и ценностных установок личности учащегося. Сегодня происходит изменение парадигмы образования – от парадигмы знаний, умений и навыков к парадигме развития личности учащегося. Главной целью образования становиться не передача знаний и социального опыта, а развитие личности ученика. Процесс обучения в современной школе требует от учителя использования в своей работе передовых технологий, способствующих оптимизации учебного процесса, повышения интереса учащихся к изучению предмета.

В своей работе над разделом большую роль я отвожу информационно-коммуникативным технологиям – использование электронно-образовательных ресурсов(ЭОР), что позволяет усовершенствовать традиционные методы обучения.

Традиционные методы обучения, используемые в организации деятельности учащихся

Традиционные средства и их дидактические возможности

Совершенствование за счёт применения ЭОР

Словестные:
рассказ, беседа, объяснение,

Устное слово, печатное слово (учебник, учебное пособия, книги). Ведущее средство – живое слово, которое легко сочетается с другими средствами обучения, позволяет в сжатые сроки обогатить память учащихся обобщенными научными знаниями

Подача текстовой информации с экрана, сообщение знаний (текст читает диктор программы). Возможность многократного повторения страниц учебного материала. Гиперссылки позволяют быстро найти нужную информацию.

Таблицы, плакаты, схемы, иллюстрации. Статичная демонстрация с экрана.

Мультимедийный показ приёмов и операций; виртуальное преобразование функций на плоскости; визуализация процессов, невозможных для рассмотрения реальных условиях. В данном случае учебная информация лучше усваивается.

Практические:
упражнения, практические и самостоятельные работы

Учебные задания для практической работы, решение задач, обучающие и проверочные самостоятельные работы

Виртуальное практическое действие, плоскостное моделирование функций, автоматизация отдельных операций. Происходит логическая обработка практического материала, уменьшается количество организационных моментов

В работе над данным разделом программы я использую следующие ЭОР: электронные учебные модули (ЭУМ), размещённые на федеральных образовательных порталах.

Электронные учебные модули, используемые при изучении раздела «Тригонометрические уравнения»

• Определение тригонометрических уравнений;
• Определение простейших тригонометрических уравнений;
• Определение однородного тригонометрического уравнения;
• Метод разложения на множители;
• Метод замены переменной;
• Метод введения вспомогательного аргумента;
• Метод рационализации.

• Решение простейших тригонометрических уравнений;
• Решение тригонометрических уравнений методом разложения на множители;
• Решение тригонометрических уравнений методом замены переменной;

• Решение тригонометрических уравнений методом введения вспомогательного аргумента;

• Решение тригонометрических уравнений методом рационализации;
• Решение однородных тригонометрических уравнений I – II степени.

• Решение простейших тригонометрических уравнений. К1
• Решение тригонометрических уравнений различными способами. К2

При работе над данным разделом программы мною используются такие технологии как проблемное обучение, развивающее обучение, дифференцированный подход в обучении.

Проблемное обучение – организация учебного процесса, который предполагает создание проблемных ситуаций и активной деятельности учащихся по их разрешению под руководством учителя. Тригонометрия предоставляет огромный материал для создания проблемных ситуаций – это классификация задач, способы решения и отбора корней. В качестве примера мы возьмем решение простейших тригонометрических уравнений. Перед классом ставится проблема: «Любое ли тригонометрическое уравнение можно решить с помощью числовой окружности или графически?». Предлагается учащимся решить уравнения: а) cost=0,4

Развивающее обучение — осуществляется в форме вовлечение детей в общий труд обучения, вызывая чувство успеха, развития. Я использую такие виды деятельности: дискуссии, методы обучения, направленные на развитие мышления, памяти, математически грамотной речи. Суть развивающего обучения состоит в том, что ученик не только усваивает знания, умения и навыки, но овладевает способами действий. Для этого я использую такой вид работы, как решение задач по тестам. Мной составлены презентации к урокам, в которых задачи подобраны по принципу «от простого к сложному». В ходе дискуссии ученики выделяют необходимые для решения задач элементы, выстраивая при этом логически обоснованные решения. Для усиления познавательного интереса к решению тригонометрических задач и поощрения учащихся, применяю кубик – «экзаменатор», лист учета знаний.

Развертка кубика-«экзаменатора»

Принципы развивающего обучения используются в ЭУМ практического типа.

Дифференцированный подход осуществляется мною на основании учёта уровня обученности, развития учащихся. Этот подход проявляется в подборе заданий разной степени сложности для разных категорий учащихся. Для домашних, самостоятельных и контрольных работ задания разбиты на две группы по уровням сложности:

I уровень – задачи, для решения которых достаточно уметь применять основные тригонометрические формулы и использовать простейшие алгоритмы, делать простые обобщения;

II уровень – задачи предназначены для наиболее подготовленных учащихся. При решении этих задач требуется иметь достаточно высокий уровень развития вычислительных навыков и навыков проведения алгебраических преобразований

6.Календарно-тематическое планирование по разделу .

📺 Видео

ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ - Решение Тригонометрических уравнений / Подготовка к ЕГЭ по МатематикеСкачать

ТРИГОНОМЕТРИЯ С НУЛЯ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

ТРИГОНОМЕТРИЧЕСКИЕ НЕРАВЕНСТВА 10 класс тригонометрияСкачать

Решение тригонометрических неравенств. 10 класс.Скачать

Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Тригонометрия в ЕГЭ может быть простойСкачать

Решение тригонометрических неравенств. 10 класс.Скачать

Тригонометрические уравнения. ЕГЭ № 12 | Математика | TutorOnline tutor onlineСкачать

Тригонометрия для Чайников, 10 класс, Уравнения, Урок 7Скачать

Тригонометрия в ЕГЭ. Задания № 4, 12. 10-11 класс. Вебинар | МатематикаСкачать

Профильный ЕГЭ 2024. Задача 12. Тригонометрические уравнения. 10 классСкачать

Простейшие тригонометрические уравнения. y=sinx. 1 часть. 10 класс.Скачать

Решение тригонометрических неравенств. 10 класс.Скачать

Решение тригонометрических уравнений. Однородные уравнения. 10 класс.Скачать

Решение тригонометрических неравенств. 10 класс.Скачать