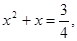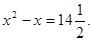Методика изучения квадратных уравнений курсовая работа

Выпускная квалификационная работа

Методические особенности изучения квадратного трехчлена на уроках алгебры в 7-9 классах

ВВЕДЕНИЕ. КВАДРАТНЫЙ ТРЕХЧЛЕН.1 Понятие квадратного трехчлена и квадратичной функции.2 Решение квадратных уравнений.3 Решение квадратных неравенств.4 Решение квадратных уравнений и неравенств с параметрами. Методика изучения квадратного трехчлена в основной общеобразовательной школе

квадратное уравнение трехчлен квадратичная функция

Тема «Квадратный трехчлен» занимает в курсе алгебры одно из центральных мест. Задания по этой теме — непременный атрибут любого экзамена, и вступительных экзаменов в вуз, в частности.

Главной целью занятий по математике является расширение и углубление знаний, развитие интереса учащихся к предмету, развитие их математических способностей. Процесс обучения основан на совместной исследовательской деятельности учащихся.

Большую роль в развитии математического мышления учащихся на занятиях играет изучение темы «Квадратный трехчлен». Это понятие вообще является одной из основных в школьном курсе математики. Но в реализации этой линии в частности, как? и когда? знакомить учащихся с понятием «квадратный трехчлен», возможны различные подходы и точки зрении.

Впервые о квадратном трехчлене говорится в 7 классе. После этого линия квадратного трехчлена постоянно поддерживается.

Поэтому квадратный трехчлен играет большую и важную роль не только в школьном курсе алгебры, но и в дальнейшем обучении в учебных заведениях. Задачи по этой теме так же непременно включают в варианты вступительных экзаменов в ВУЗы. И хочется отметить важность этого небольшого раздела школьного курса заключается в его чрезвычайно широких областях применения.

Тема моей курсовой работы: «Методические особенности изучения квадратного трехчлена на уроках алгебры в 7 — 9 классах».

Цель исследования: Проанализировать степень усвоения квадратного трехчлена на примерах заданий на повторение.

Область исследования — элементарная математика.

Объект исследования — алгебра.

Предмет исследования — квадратичная функция.

Рассмотреть тематическое планирование по разным учебникам.

Проанализировать степень трудности заданий по одному из учебников.

Проанализировать степень усвоения данной темы на примерах заданий на повторение.

Гипотеза: Если на каждом уроке алгебры выполнять с учащимися задания, связанные с квадратным трехчленом, то степень усвоения квадратного трехчлена значительно улучшится.

Глава I. КВАДРАТНЫЙ ТРЕХЧЛЕН

I.1 Понятие квадратного трехчлена и квадратичной функции

В различных источниках, понятие «квадратного трехчлена», дается по — разному. В одних, квадратный трехчлен — это многочлен второй степени с одной переменной

где x- переменная; a,b — коэффициенты, с- свободный член, a ¹ 0. В других, квадратным трехчленом относительно x называется выражение вида ax 2 +bx+c, где a,b,c — некоторые числа, причем a ¹ 0. Числа a,b,c называются коэффициентами квадратного трехчлена. В дальнейшем будем предполагать, что a,b,c — действительные числа.

Значения x, при которых квадратный трехчлен ax 2 + bx + c обращается в нуль, называются корнями трехчлена. Таким образом, для нахождения корней квадратного трехчлена нужно решить квадратное уравнение:

ax 2 + bx + c = 0. (2)

Напомним, каким образом находятся корни квадратного уравнения; при этом мы несколько уточним факты, обычно излагаемые в школьном курсе. Для решения квадратного уравнения пользуются приемом «выделение полного квадрата», то есть записывают его в виде (напомним, что a ¹ 0):

ax2 + bx + c = a(x2 + x) + c = a (x2 + 2x) + c = a (x2 + 2x + ) + c — = a (x + )2 —

Таким образом, уравнение ax 2 + bx + c=0 можно записать в виде:

Или (перенося дробь в правую часть и поделив на a ) в виде:

При этом уравнение (3) равносильно уравнению ax 2 + bx + c = 0, то есть имеет те же корни, что и уравнение ax 2 + bx + c.

В самом деле, если некоторое число x удовлетворяет уравнению

то как показывают проведенные выкладки, оно удовлетворяет и уравнению (3) . Но эти выкладки можно провести и в обратном порядке, то есть если число x удовлетворяет уравнению (3), то оно удовлетворяет и уравнению

Иными словами, равенство ax 2 + bx +c = 0 представляет собой неопределенное высказывание, которое для одних значений x (а именно для корней трехчлена) является истинным, а для других — ложным. Эквивалентность уравнений

ax 2 + bx + с = 0 и (3) заключается в том, что эти два неопределенных высказывания одновременно истинны и ложны. Итак, остается решить уравнение (3). Обычно число b 2 — 4ac обозначают через «D» и его называют дискриминантом квадратного трехчлена.

Таким образом, уравнение (3) можно записать так:

(x + )2 =, где D=b2- 4ac (4)

Теперь предлагаются три различных случая — в зависимости от того, каким является число D:

А) Если число D положительно, то положительно и число . Поэтому существуют два числа, квадрат каждого из которых равен : это будут числа и -(где, как всегда, — арифметический корень из положительного числа D). Но согласно (4) x+ как раз есть такое число, квадрат которого равен . Значит, x удовлетворяет уравнению (4) в двух случаях:

) если x + = (и тогда x = )

) если x + = (и тогда х = )

Итак, при D>0 уравнение (4), а значит и уравнение ax2 + bx + c = 0, имеет два корня:

X1=, X2=, Где D=b2-4ac (5)

Заметим, что в этом случае оба корня x 1 , x 2 действительны, причем x 1 ¹ x 2 (то есть уравнение в самом деле имеет два корня).

Б) если число D равно нулю, то уравнение (4) принимает вид:

Но квадрат числа равен нулю только в том случае, если само число равно нулю, и поэтому мы отсюда получаем

Итак, при D=0 уравнение (4), а значит и уравнение x2 + bx + c = 0, имеет только один корень x = -, то есть существует только одно число ( а именно -), удовлетворяющее этому уравнению. Однако в целях единообразия считают, что и в этом случае уравнение ax2 + bx + c = 0 имеет два корня, только они оба совпадают. Иными словами, условно считают, что и при D = 0 уравнение ax2 + bx + c = 0 имеет два корня:

Заметим, что то же получается и из формул (5), поскольку D = 0. Таким образом, если мы условимся при D = 0 считать корень X = — два раза (или, как еще говорят, уславливаемся считать его двукратным корнем), то формулы (5) для корней сохраняют силы и в этом случае. Мы увидим, что и во многих дальнейших случаях это соглашение (считать при D = 0 корень двукратным) оказывается очень удобным: иначе во многих теоремах приходилось бы делать специальные оговорки, относящиеся к этому случаю. Поэтому в математике всегда принято считать, что при D = 0 уравнение ax2 + bx + c = 0 имеет два совпадающих корня. Однако отдаем себе ясный отчет в том, что это лишь условное соглашение: при D = 0 из всех действительных чисел только одно ( а именно — ) удовлетворяет уравнению ax2 + bx + c = 0.

В) Осталось рассмотреть случай, когда D отрицательно. В этом случаи и число отрицательно. А так как квадрат действительного числа не может быть отрицательным, то, значит, в этом случае уравнение ax2 + bx + c = 0 не имеет действительных корней. Как мы знаем, существует два комплексных числа, квадрат каждого из которых равен отрицательному числу D. Эти числа являются чисто мнимыми и притом сопряженными. Если мы условимся одно из них (безразлично, какое) обозначать через , то другое будет равно

. Тогда числами, квадрат каждого из которых равен отрицательному числу ,будут чисто мнимые числа и — (а других таких чисел не существует). Но согласно (4) x + есть число, квадрат которого равен.

Следовательно, x удовлетворяет уравнению (4), а значит и уравнению

ax2 + bx + c = 0, в двух случаях:

)Если x + (и тогда x = );

)Если x + (и тогда x = ).

Таким образом, и в этом случае (то есть при D 2 + bx + c (6)

где a ?0, b и c — постоянные, а переменная x принадлежит множеству R действительных чисел, называется квадратичной функцией.

Из определения ясно, что квадратичной является и каждая из функций

F(x) = ax 2 + bx, ( где b = 0, с?0),

y = ax 2 + c , (где b=0, c = 0)

Это тождество легко доказать преобразованием правой части. Немного труднее преобразование левой части путем выделения точного квадрата. Используя это утверждение и равенство (6), можно записать такую схему:

На основании равенства (7) легко доказать следующее утверждение:

Квадратичная функция при:

А) a>0 имеет глобальный минимум

Б) a 0 является самой нижней точкой графика функции, а при a 0 убывает на промежутке

D1 = (- ?; -] и возрастает на промежутке 2 = [- ; + ?);

б) a 0 на интервале D1 убывает. Дадим произвольные различные значения x1 и x2 переменной, и для определенности пусть

На основании (8) последовательно находим

x1 + -(x2 + ) > 0, (x1 + )2 > (x2 + )2,(x1 + )2 + > a (x2 +)2 + ,

то есть f (x 1 ) > f (x 2 ). Следовательно, на интервале D 1 квадратичная функция убывает.

К этому выводу короче можно прийти следующими рассуждениями:

f (x2) — f (x1) = a (x — x) + b (x2 — x1) =

( x2 — x1) (a (x2 + x1) + b) f (x2).

Аналогичным образом рассматриваем и остальные случаи. При помощи производной функции утверждения 3 можем доказать, используя необходимое и достаточное условие убывания или возрастания функции. Утверждение 2 доказывается с использованием производной функции, точнее, с помощью достаточного условия существования локального экстремума.

Далее, предварительно вспомнив определение графика функции, можем приступить к изучению свойств графика квадратичной функции с рассмотрения еще одного утверждения.

График квадратичной функции f(x) = ax2 + bx + c симметричен относительно прямой q0, которая проходит через точку А (-; 0) и параллельна оси ординат (или совпадает с ней).

Чтобы доказать это утверждение, даем два произвольных значения x1 и x2 переменной, симметричных относительно точки x0 = -, и, используя равенство (7), находим, что соответствующие значения функции равны. Можем также дать произвольное значение x3 переменной, получив точку P(x3; f(x3)) графика функции, и показываем, что точка Q, симметричная точке P относительно прямой q0, тоже принадлежит графику.

График квадратичной функции является кривой линией, которая называется параболой. Прямая q0 и (-; ) называются соответственно осью и вершиной параболы. Известно, что ось абсцисс содержит те и только те точки, ординаты которых равны 0. Значит, чтобы установить, при каких значениях аргумента x квадратичная функция принимает значения, равное 0, нужно проверить, имеет ли парабола хотя бы одну общую точку с осью абсцисс тогда и только тогда, когда ордината ее вершины ? 0, то есть когда b2-4ac ? 0. Число b2 — 4ac обозначается через D и называется дискриминантом, как квадратичной функции, так и квадратного уравнения:

ax 2 + bx + c = 0 (9)

Следовательно, если a>0, то:

При D>0 уравнение (9) имеет различные действительные корни x 1 и x 2 ;

При D=0 уравнение (9) имеет один действительный корень;

При D 0 возможны такие случаи:

А) При D > 0 и x1 > 0 и x 1 x 2 функция принимает значение, равное 0, для значений переменной x 1 и x 2 , отрицательные значения для каждого

x Î ( — ¥ ; x 1 ) È ( x 2 ; + ¥ ), положительные значения для каждого Î ( — ¥ ; x 1 ) È ( x 2 ; + ¥ ), положительные значения для каждого x Î ( x 1 ;x 2 ).

Б) При D = 0 функция принимает значение, равное 0, только для значения переменной x1 = x2 = -, отрицательные значения для каждого x ¹ — ;

В) При D 2 + bx + c = 0.

Числа a, b и c называются коэффициентами квадратного уравнения; из них — первый коэффициент, или коэффициент при старшем члене, b — второй коэффициент, или коэффициент при неизвестном в первой степени, c — свободный член. Число x 0 , обращающее квадратный трехчлен ax 2 + bx + c в нуль, называется корнем квадратного трехчлена, а также и корнем квадратного уравнения

Квадратное уравнение, у которого первый коэффициент равен 1, то есть уравнение вида

Для приведенного квадратного уравнения x 2 + px + q = 0.

Формула корней имеет вид:

а для уравнения ax 2 + b + c = 0 ( с четным коэффициентом при x ) — вид

Для коэффициентов и корней квадратного уравнения ax 2 + b + c = 0, где a? 0 выполняются соотношения:

Эти соотношения называют теоремой Виета, по имени французского математика Ф. Виета (1540 — 1603г).

Особенно удобна эта теорема для приведенного квадратного уравнения:

x 1 + x 2 = — p ; x 1 x 2 = q

Уравнение второй степени умели решать еще в Древнем Вавилоне во 2-ом тысячелетии до н. э. Математики Древней Греции решали квадратные уравнения геометрически; например, Евклид — при помощи деления отрезка в среднем и крайнем отношениях.

Например, корни трехчлена y = 2×2 — 5x — 3 равны x1 = — и x2 = 3,

так как y(-) = 2(-)2 — 5(-) — 3 = 0

и y(3) = 2 × 32 — 5 × 3 — 3 = 0

По — другому мы скажем, что квадратное уравнение 2×2 — 5x — 3 = 0 имеет два корня: x1 = -; x2 = 3.

Неполные квадратные уравнения.

Типы неполных квадратных уравнений.

Если в квадратном уравнении общего вида ax2 + bx + c = 0 один из двух коэффициентов, b или c, равен нулю или оба одновременно равны нулю, то квадратное уравнение называется неполным.

Возможны три типа неполных квадратных уравнений:

1) ax 2 + bx + c = 0 ( c = 0, a ? 0, b ? 0 )

2) ax 2 + c = 0 ( b = 0, a ?0, c ? 0 )

) ax 2 = 0 ( a ? 0, b = c = 0 ).

Решение неполных квадратных уравнений.

1) Уравнение ax 2 + bx = 0 решается разложением левой части на множители:

x (ax + b ) = 0. Произведение обращается в нуль, если один из множителей равен нулю; поэтому либо x = 0, либо ax + b = 0, откуда x = -.

Итак, неполное квадратное уравнение ax2 + bx + c = 0 имеет два корня:1 = 0, x2 = —

4×2 — 3x = 0, x1 = 0, x2 =

) Уравнение ax2 + c = 0 почленным делением на a и члена в правую часть приводим к виду: переносом свободного

Если коэффициенты a и c имеют противоположные знаки, то аx 2 = 0, a ? 0, то x 2 = 0, x = 0. Говорят, что число 0 является двукратным корнем уравнения ax 2 = 0, то есть x 1 = x 2 = 0.

Уравнение четвертой степени, содержащее только четные степени неизвестного, называется биквадратным . Общий вид такого уравнения

ax 4 + bx 2 + c = 0 (a ? 0 ).

Решение такого уравнения сводится к решению двух квадратных уравнений, о чем говорит само название (биквадратное означает «двойное квадратное»). Отметим, что если биквадратное уравнение имеет корень x 0 , то оно имеет также и корень — x 0 , то есть корни биквадратного уравнения попарно противоположны.

В самом деле, если x 0 есть корень, то подстановка в уравнении н6а место x числа x 0 дает справедливое равенство

но тогда справедливо и другое равенство:

a (- x 0 ) 4 + b (- x 0 ) 2 + c = 0, (2)

так как левые части у равенств (1) и (2) одинаковы.

Чтобы решить биквадратное уравнение, введем вспомогательное неизвестное z, полагая z = x 2 , z 2 = x 4 . Тогда уравнение примет вид

Это — квадратное уравнение относительно вспомогательного неизвестного z, и его корни

Но z 1 = x 2 и z 2 = x 2 , откуда

Таким образом, биквадратное уравнение имеет четыре корня, причем корни x 1 и x 2 , x 3 и x 4 попарно противоположны, то есть сумма каждой пары корней равна нулю, а потому и сумма всех четырех корней равна нулю.

Эти формулы можно объединить в одну:

Пример. 2x 4 — 19x 2 + 9 = 0.= x 2 , 2z 2 — 19z + 9 = 0,

z1 =, z2 = 9; x1,2 = , x3,4 = 3.

Исследование корней биквадратного уравнения.

Характер корней биквадратного уравнения

ax 4 + bx 2 + c = 0 (3)

зависит от того, каковы корни вспомогательного квадратного уравнения

az 2 + bz + c = 0 (4)

1. Предположим, что a >0 и дискриминант уравнения (4) положителен: = b 2 — 4ac > 0. Тогда при c > 0 и b 1 > 0 и z 2 > 0, и биквадратное уравнение (3) имеет четыре действительных корня, так как

2. Если a > 0, D > 0, c > 0 и b > 0 , то z 1 2 0, D > 0, c 1 2 > 0, поэтому одна пара корней x 3 и x 4 — действительная, другая x 1 и x 2 — мнимая.

Разложение квадратного трехчлена на множители.

Пользуясь свойствами корней квадратного уравнения, можно всякий трехчлен с действительными корнями разложить на множители:

ax2 + bx + c = a (x2 + x + ) = a [x2 — (x1 + x2)x + x1x2] = a [(x2 — x1x2) — (x2x — x1x2)] = a [x (x — x1) — x2 (x — x1)] = a (x — x1) (x — x2).

x2 + 5x — 3 = 2 (x + 3) (x — ).

Корни трехчлена: x1 = -3, x2 = .

Таким образом, мы рассмотрели различные виды квадратных уравнений, которые тесным образом связаны с квадратным трехчленом.

I.3 Решение квадратных неравенств

ax 2 + bx + c = 0,(1)

где а, b, с — действительные числа, а ? 0, будем называть квадратным неравенством.

Если вместо x в левую часть неравенства (1) подставить некоторое действительное число x0, то получим числовое неравенство ax + bx0 + c > 0, которое при одних значениях x0 может оказаться верным, а при других — неверным.

Иначе говоря, неравенство (1) можно рассматривать как неопределенное высказывание, которое для одних значений x является истинным, а для других — ложным. Число x 0 назовем решением неравенства (1), если при подстановке вместо x числа x 0 получается верное числовое неравенство ax 2 + bx + c > 0, то есть если квадратный трехчлен ax 2 + bx + c при x = x 0 принимает положительное значение.

Решить неравенство (1) — значит найти все решения этого неравенства.

Если использовать график функции y = ax 2 + bx + c, то решение неравенства (1) сводится к отысканию всех тех значений x для которых точки графика функции y + ax 2 + bx + c лежат выше оси абсцисс.

Наряду с неравенствами вида (1) можно рассматривать, например, такие неравенства:

aх 2 + bх + с ? 0, (3)

ax 2 + bx + c ? 0, (4)

a 1 x 2 + b 1 x + с 1 > а 2 х 2 + b 2 х + с 2 (5)

Эти неравенства мы также будем называть квадратными (если в (5) а 1 = а 2 , то это неравенство становится линейным).

Введем следующее определение. Два квадратных неравенства будем называть равносильными, если эти неравенства имеют одни и те же решения, то есть если всякое решение первого неравенства является решением второго и, обратно, всякое решение второго неравенства является решением первого.

Из этого определения следует, что

а)неравенство ax 2 + bx + c 2 + bx + c > 0;

б)неравенство a 1 x 2 + b 1 x + c 1 > a 2 x 2 + b 2 x + c 2 равносильно неравенству

(a 1 — a 2 ) x 2 + ( b 1 — b 2 ) x + c 1 — c 2 > 0

(при любых действительных a 1 , a 2 , b 1 , b 2 , c 1 , c 2 ).

Докажем, например, первое из этих утверждений.

Пусть x0 — решение неравенства ax2 + bx + c 0, откуда видно, что x0 — решение неравенства — ax2 — bx — c > 0.

Обратно, если x 1 — решение неравенства — ax 2 — bx — c > 0,

то — ax — bx1 — c > 0 — верное числовое неравенство, откуда находим ax + bx1 + c неравенств, то есть неравенств, содержащих знаки « > » или «

Заметим, что всякое строгое квадратное неравенство можно привести к одному из следующих видов:

a) ax 2 + bx + c >0 при a >0; (6)

б) ax 2 + bx + c 0. (7)

Действительно, если a 2 + bx + c > 0, по доказанному выше, равносильно неравенству

a 1 x 2 + b 1 x + c 1

где a 1 = -a, b 1 = -b, c 1 = -c, причем a 1 > 0 (то есть равносильно неравенству вида (7)).

Аналогично, при а 2 + bx + c

Итак, рассмотрим неравенства (6) и (7), в которых, а > 0.

Исследование квадратного трехчлена позволяет утверждать, что

) если D а неравенство (7) не имеет решений.

2)если D=0, то неравенство (6) имеет место при всех x, кроме x = — ,

а неравенство (7) не имеет решений;

3)если D > 0, то неравенство (6) выполняется при x 1 и x > x 2

( то есть вне отрезка [ x 1 , x 2 ], где x 1 2 — корни трехчлена),

а неравенство (7) выполняется при x 1 2 ( т о есть на интервале ( x 1 , x 2 )).

Итак, при а > 0 неравенство ax 2 + bx + c > 0 выполняется всегда, кроме случая, когда ? 0 и x 1 ? x ? x 2 , а неравенство ax 2 + bx + c 0 имеет место лишь тогда, когда > 0 и x 1 .

Пример 6. Решить неравенство x 2 — 5x + 6 > 0.

Решение. Имеем D = 5 2 — 6·4=1 > 0.

Решив уравнение x 2 — 5x + 6 = 0, находим его корни: x 1 = 2, x 2 = 3.

Так как, а= 1 > 0, то неравенство имеет место при x 3.

Этот же результат можно получить из разложения 2 — 5x + 6 = (x — 2)(x — 3).

Наконец, решение неравенства можно найти графически: график функции = x 2 — 5x + 6 пересекает ось Оx в точке x 1 = 2 и x 2 = 3 и расположен выше оси Оx при x 3.

Пример 7. Решить неравенство 6x — 9 2 .

Решение. Неравенство равносильно следующему: 2 — 6x + 9 >0 или ( x — 3) 2 > 0;

оно выполняется при всех x, кроме x = 3.

Пример 8. Решить неравенство 2х 2 + 4x + 3

Решение. Так как D=16 — 24 0, то данное неравенство не имеет решений.

Пример 9. Решить неравенство x 2 ? 4x — 4.

Решение. Неравенство равносильно следующему: x 2 — 4x + 4 ? 0 или

( x-2) 2 ? 0; оно имеет место лишь при x = 2.

Таким образом, можно сделать вывод, что квадратные неравенства, которые тесным образом связаны с квадратным трехчленом, имеют не маловажное значение и играют очень важную роль при сдаче ЕГЭ и при поступлении в Вузы, а также играют большую роль в развитии математического мышления учащихся и вызывают интерес к теме.

I.4 Решение квадратных уравнений и неравенств с параметрами

Решения квадратных уравнений и неравенств с параметрами

Квадратные уравнения и неравенства — одни из важнейших понятий математики. В большинстве практических и научных задач, где какую — то величину нельзя непосредственно измерить или вычислить по готовой формуле, удается составить соотношение (или несколько соотношений), которым оно удовлетворяет. Так получают уравнение (или систему уравнений) для определения неизвестной величины.

Квадратные уравнения и неравенства с параметрами встречаются во многих вступительных и выпускных экзаменах. Но в учебниках школьного курса слишком мало практики, на мой взгляд, для успешного выполнения данных уравнений и неравенств на экзамене.

Рассмотрим несколько примеров квадратных уравнений и неравенств с параметрами, чтобы лучше понять, в чем состоит суть их решения.

При решении квадратных уравнений с параметрами рассматриваются два случая:

1) Первый коэффициент равен нулю, тогда квадратное уравнение превращается в линейное;

2) Первый коэффициент не равен нулю.

Решим уравнение 1.

(a — 1) x 2 + 2 (2a +1) x + (4a + 3) = 0

Решение. В данном случае контрольным является значение a = 1. Дело в том, что при a = 1 это уравнение является линейным, а при a ? 1 оно квадратное (в этом и состоит качественное изменение уравнения.) Значит, целесообразно рассмотреть уравнение как семейство уравнений, получающихся из него при следующих значениях параметра: 1) a = 1; 2) a ? 1.

Рассмотрим эти случаи.

1) При a = 1 уравнение примет вид 6x + 7 = 0.

Из этого уравнения находим x = -.

2) Из множества значений параметра a ? 1 выделим те значения, при которых дискриминант уравнения обращается в 0.

Дело в том, что если дискриминант D = 0 при a = a 0 , то при переходе значения D через точку a 0 дискриминант может изменить знак ( например, при a a 0 D > 0). Вместе с этим при переходе через точку a 0 меняется и число действительных корней квадратного уравнения ( в нашем примере при a a 0 корней нет, так как D 0, а при a > a 0 D > 0 уравнение имеет два корня). Значит, можно говорить о качественном изменении уравнения. Поэтому значения параметра, при которых обращается в 0 дискриминант квадратного уравнения, также относят к контрольным значениям.

Составим дискриминант уравнения:= 4 (2a + 1) 2 — 4 ( a — 1)( 4a + 3 ) = 16a 2 + 16a + 4 — 16a 2 + 16a — 12a + 12 = 20a + 16 = 4 (5a +4 )

При a = -, D = 0; уравнение имеет корень x =

При a — , D > 0 уравнение имеет два различных действительных корня.

Таким образом, если a 2 — 1| + |x 2 — x — 2| — x — a = 0 имеет три различных корня.

Переписав уравнение в виде | x 2 — 1|+|х 2 — x — 2|= x + a и рассмотрев пару функций(x) =|х 2 -1|+| x 2 — x — 2|, g(x) = x + a, можно заметить, что искомые значения параметра а и только они будут соответствовать тем положениям графика функции g(x), при которых он имеет точно три точки пересечения с графиком функции f(x).

. Найти все значения параметра a.

ax 2 + 2x(a +3) + a + 2 = 0,

пусть x1, x2 — корни уравнения 1×2 =

так как x1 ? 0 и x2 ? 0, то 1,2 ? 0 и x1 + x2 ? 0

Ответ: x ? 0 при a Î [ -3 ; -2 ] .

Таким образом, для успешного решения уравнений с параметрами необходимо последовательно рассматривать решение от простых уравнений, решение которых можно изобразить графически к более сложным уравнениям, где требуется абстрактное представление и выбор конкретного решения.

Способы решений неравенств с параметрами.

1) При каких значениях параметра a имеет решение система

x 2 + (5a +2)x + 4a 2 + 2a 0 (1)

Найдем корни трехчлена левой части неравенства —

x 1 = -4а — 2, х 2 = -а(*)

Прямые, заданные равенствами (*), разбивают координатную плоскость аОх на четыре области, в каждой из которых квадратный трехчленx 2 + (5a + 2)x + 4a 2 + 2a = (x + 4a + 2)(x + a)

сохраняет постоянный знак. Уравнение (2) задает окружность радиуса 2 с центром в начале координат. Тогда решением исходной системы будет пересечение заштрихованной области с окружностью, где Î (a 1 ; a 2 ) È ( a 3 ; a 4 ), а значения a 1 и a 4 находятся из системы

x + a = 0 2 + a 2 = 4

а значения a 1 и a 4 находятся из системы+ 4a + 2 = 0 2 + a 2 = 4

Решая эти системы, получаем, что

a1 = , a4 = , a2 = -, a3 = 0.

Ответ: a Î ( — ) È ( 0; ).

2) Решить неравенство

Находим ОДЗ или линии разрыва (асимптоты)

a — 3 ? 0 2x + 1 ? 0? x ? —

Найдем уравнения функций, графики которых нужно построить в ПСК; для чего перейдем к равенству:

Разложим числитель на множители:2 — 3а + 2 = 0

т. к. а1 = 1, а2 = 2, то

Разделим обе части равенства на (1 — a) при a ? 1. Но a = 1 является решением: левая часть уравнения равна правой части и равна нулю при Î R.

ax + 2a — 3x -3 = 2ax + a — 4x — 2= 1- x

Строим в ПСК хОа графики функций

a ¹ , x ¹ , a = 1, x = 1- a

и нумеруем образовавшиеся области (оси роли не играют). Получилось девять областей.

Ищем, какая из областей подходит для данного неравенства, для чего берем точку из области и подставляем в неравенство.

Для наглядности составим таблицу.

вывод1( 2; 0)0 £ -1-2 ( 2; — )0 £ + 3( 2; -2 )0 £ -4( ; -1 ) £ 0 + 5( 0; -1) £ 0-6( 0; 0 ) £ 1+7( 0; 2 ) -8( ; 0 ) +

Найдем точки пересечения графиков

Зададим прямую a = сonst и будем сдвигать её от — ¥ до + ¥.

при a 1 — a £ x 2 и y = x 3 , в теме «Одночлены», тем самым, подготавливая учащихся к изучению темы «Квадратный трехчлен», в главе: «Степень с натуральным показателем», на которую отводится 18 часов. Рассмотрим фрагмент урока:

Ребята, вы изучали функцию, которая задается уравнением вида

y = kx + m с двумя переменными x, y.

Какую функцию задает это уравнение?

Как вы думаете, не встречаются ли математические модели такого же плана, но такие, у которых «y» выражается через «x» не по формуле y = kx + m, а иным способом?

Пусть x — сторона квадрата, а y — его площадь. Как выразить y через x?

Пусть x — сторона куба, а y — его объем. Как выразить y через x?

Говоря об учебнике 7 класса, под редакцией А. Г. Мордковича, можно сказать, что на изучение данной темы отводится отдельная глава «Функция y = x 2 »:

1. Функция y = x 2 и ее график.

2. Графическое решение уравнений.

3. Что означает в математике запись y = f (x).

Но следует отметить тематическое планирование по учебнику «алгебра 7-го класса» под редакцией А. Г. Мордковича, рассчитывая по 3 часа в неделю. Основная цель: дать учащимся представление о том, что в математике, кроме линейных функций встречаются и другие функции, например y = x 2 и кусочные функции; познакомить учащихся еще с двумя свойствами функций: непрерывность функции, область определения функции; показать, как можно использовать графики функций для решения уравнений.

Глава: Функция y = x 2 :

1. Функция y = x 2 и ее график. На эту тему отводится 2 часа,

2. Графическое решение уравнений — 2 часа,

. Что означает в математике запись y = f (x)? — 3 часа,

. Контрольная работа — 1 час,

. Итоговое повторение и итоговая контрольная работа — 1 час,

Таким образом, на эту тему отводится 9 часов. Эта тема рассматривается в более широком контексте, чем в учебнике под редакцией Ю. Н. Макарычева. Рассмотрим план изучения данной темы:

1. Познакомить учащихся с графическими моделями, отличными от линейной функции.

2. Построить график функции y = x 2

. Исследовать свойства функции и особенности ее графика.

Также первое упоминание квадратного трехчлена в 7-ом классе можно проследить в теме: «Разложение многочлена на множители», в подразделе «Разложение многочлена на множители с помощью способа группировки». Рассмотрим фрагмент урока:

— Решим уравнение x 2 — 7x + 12 = 0.

Прежде чем решить это уравнение нам нужно разложить на множители многочлен или как правильно сказать квадратный трехчлен, где в 8 классе вы будете подробно рассматривать его.

Нам предлагают разложить многочлен способом группировки, как вы уже заметили, что для способа группировки необходимо 4 члена, а в данном случае — только 3. Поэтому здесь можно представить слагаемое -7x, в виде суммы -3x-4x, и получится не три слагаемых, а уже четыре.

Эти слагаемые можно распределить по двум группам: 2 -7x + 12 = x 2 — 3x — 4x + 12 = (x 2 — 3x) + (-4x + 12) = x(x — 3) — 4(x — 3) = (x — 3)(x — 4).

А теперь заданное уравнение перепишем так

(x — 3)(x — 4) = 0- 3 = 0 или x — 4 = 0= 3 x = 4

Итак, заданное уравнение имеет 2 корня.

Конечно, нахождение корней квадратного трехчлена можно найти по специальной формуле, с которой вы познакомитесь на следующий год.

Тем самым мы выяснили, что основа темы «Квадратного трехчлена» начинает изучаться с 7-го класса и играет важную роль при дальнейших изучениях ее в последующих классах.

Если в 7 классе мы рассматривали тему «Квадратный трехчлен» в общих чертах, то в 8, 9 классах происходит дробление данной темы на более широкие подпункты. А именно, изучение данной темы, в учебнике под редакцией Ю.Н. Макарычева, изучается в 9 классе, в теме «Квадратичная функция», на которую отводится 25 часов:

. Функция. Область определения и область значений функции. (3ч)

.Свойства функции. (3ч)

. Квадратный трехчлен и его корни. (1ч)

. Разложение квадратного трехчлена на множители. (3ч)

. Функция y = ax 2 , ее график и свойства. (2ч)

. Графики функций y = ax 2 + n и y = a (x — m) 2 . (2ч)

. Решение неравенств второй степени с одной переменной. (3ч)

. решение неравенств методом интервалов. (3ч)

. Итоговый урок. Решение задач. (1ч)

Основная цель — выработать умение строить график квадратичной функции и применять графические представления для решения неравенств второй степени с одной неизвестной.

Изучение данной темы используется для систематизации расширения сведений о функциях. При изучении вопроса о квадратном трехчлене и его разложении на множители специальное внимание рекомендуется уделить задачам, связанным с выделением квадрата двучлена из квадратного трехчлена. Изучение квадратичной функции начинается с рассмотрения функции y = ax 2 , ее свойств и особенностей графика, а также других частных видов квадратичной функции — функций y = ax 2 + b; y = a (x — m) 2 . Эти сведения используются при изучении свойств квадратичной функции общего вида. Важно, что бы учащиеся понимали, что график функции y = ax2 + bx + c может быть получен из графика функции = ax 2 с помощью двух параллельных переносов вдоль осей. Приемы построения графика функции y = ax2 + bx + c отрабатывается на конкретных примерах. При этом следует уделять внимание формированию умения указывать координаты вершины параболы, ее ось симметрии, направление ветвей параболы.

Формирование умений решать неравенства вида ax 2 + bx + c > 0, 2 + bx +c

1. Ввести понятие квадратного трехчлена, корня квадратного трехчлена, дискриминанта квадратного трехчлена.

2. Рассмотреть примеры:

Выделить из трехчлена: a) 2x 2 — 4x + 6) 3x 2 — 36x + 140

. Закрепление нового материала.

Задания по — вариантам, проверка решения — у доски.- вариант: Число 3 — ?2, II — вариант: Число -?7 + 2

являются корнем квадратного трехчлена x 2 — 6x + 7?

Говоря об учебнике, под редакцией А. Г. Мордковича, данная тема: «Квадратный трехчлен» изучается в 8 классе, в разделе «Квадратичная функция» и делится на следующие под темы:

1. Функция y = kx 2 , ее свойства и график.

2.Функция y = , ее свойства и график.

.Как построить график функции y = f (x + l), если известен график функции y = f (x).

.Как построить график функции y = f (x) + m, если известен график функции y = f (x).

.Как построить график функции y = f (x + l) + m, если известен график функции y = f (x).

.Функция y = ax2 + bx + c, ее свойства и график.

.Графическое решение квадратных уравнений.

Основная цель — расширить класс функций, свойства и графики которых известны учащимся; продолжить формирование представлений о таких фундаментальных понятиях математики, какими являются понятия функции, ее области определения, ограниченности, непрерывности, наибольшего и наименьшего значений на заданном промежутке. В реализуемой в учебнике концепции школьного курса алгебры приоритет среди основных содержательно — методических линий отдается функционально — графической линии. Изучение любого класса функций, преобразований, уравнений выстраивается по жесткой схеме: функция — уравнения — преобразования.

И следует отметить особым вниманием, что эта тема подробнейшим образом изучается в 8 классе, не смотря на то, что она по учебнику Ю.Н. Макарычева изучается в 9 классе. Это, как я думаю, объясняется тем, что автор учебника 8 класса считает целесообразным начать изучение данной темы именно в этом классе нежели, чем в 9. Поэтому нужно отметить тематическое планирование учебника 8 класса, под редакцией А. Г. Мордковича, рассчитывая по 3 часа в неделю.

Глава: Квадратичная функция. Функция y = .

Основная цель: познакомить учащихся с функциями y = kx2, y = , = ax2 + bx + c, научить их строить графики этих функций и использовать их для графического решения уравнений, для отыскания наибольших значений функции на промежутке, для построения графиков кусочных функций.

. Функция y = kx2 , ее свойства и график. На эту тему отводится 3 часа,

. Функция y = , ее свойства и график — 2 часа,

. Как построить график функции y = f (x + l), если известен график функции y = f (x) — 2 часа,

. Как построить график функции y = f (x) + m, если известен график функции y = f (x) — 2 часа,

. Как построить график функции y = f (x + l) + m, если известен график функции y = f (x) — 2 часа,

. Функция y = ax2 + bx + c, ее свойства и график — 4 часа,

. Графическое решение квадратных уравнений — 1 час,

. Контрольная работа — 1 час.

Таким образом, нужно отметить, что на тему: «Функция y = ax 2 +bx + c, ее свойства и график», а именно «квадратный трехчлен» отводится 4 часа, тем самым отводится не мало времени, так как эта тема играет важную роль, а на всю тему: «Квадратичная функция» отводится 15 часов. Рассмотрим план изучения темы: «функция y = ax 2 + bx + c, ее свойства и график»:

1. Дать определение квадратичной функции.

2. Доказать теорему: Графиком квадратичной функции y = ax 2 + bx + c является парабола, которая получается из параболы y = ax 2 параллельным переносом

. Показать правило нахождения оси симметрии параболы.

. Выписать формулы нахождения координат вершины параболы.

. Определить направление ветвей параболы.

Построение графика лучше рассмотреть на примере функции y = -x 2 + 8x — 10.

Так как квадратный трехчлен является частным случаем квадратного уравнения, поэтому рассмотрим методику изучения «Квадратного уравнения».

В 8 классе особое место занимает изучение темы: «Квадратное уравнение», как в учебнике, под редакцией А. Г. Мордковича, так и в учебнике под редакцией Ю.Н. Макарычева.

По учебнику А. Г. Мордковича, в главу: «Квадратные уравнения», входят следующие под разделы:

1. Основные понятия: квадратное уравнение, приведенное и неприведенное уравнение, полное и неполное уравнение, дискриминант. На эту тему отводится 2 часа

2. Формулы корней квадратных уравнений — 3 часа

. Рациональные уравнения — 3 часа

. Рациональные уравнения как математические модели реальных ситуаций — 4 часа

. Еще одна формула корней квадратного уравнения — 2 часа

. Теорема Виета. Разложение квадратного трехчлена на множители — 2 часа

. Иррациональные уравнения — 3 часа.

Здесь же, я указала тематическое планирование и выяснила, что на эту тему отводится 19 часов. Основная цель: научить учащихся решать квадратные уравнения и раскладывать квадратный трехчлен на множители, научить школьников решать рациональные уравнения и текстовые задачи; познакомить учащихся с теоремой Виета и некоторыми ее приложениями и так далее.

А по учебнику, под редакцией Ю. Н. Макарычева, на которую отводится 23 часа, в тему: «Квадратные уравнения» входят следующие подразделы:

1. Квадратное уравнение

2. Формулы корней квадратного уравнения.

. Решение рациональных уравнений.

. Решение задач, приводящих к квадратным уравнениям.

Основная цель — выработать умения решать квадратные уравнения, простейшие рациональные уравнения и применять их к решению задач.

Учащиеся 8 класса имеют достаточное представление о квадратных уравнениях и умеют решать отдельные уравнения вида ax2 + bx = 0 , путем вынесения общего множителя за скобки; и ax2 + c = 0, пользуясь формулой «разность квадратов». А также в 7 классе в теме «Формулы сокращенного умножения» учащиеся выполняют задания по выделению квадрата двучлена из квадратного трехчлена, поэтому учителю необходимо на первом уроке по этой теме: систематизировать знания учащихся, дать определение квадратного уравнения, рассмотреть его виды и способы их решения.

Учащиеся должны понимать, что уравнение вида ax2 + bx + c = 0, ax2 + bx =0, ax2 + c = 0, ax2 = 0 — есть все квадратные, так как переменная величина записана во второй степени.

Особое внимание учащееся должны уяснить, что квадратное уравнение имеет корни, то их два. При выводе формулы для нахождения корней квадратного уравнения, учитель может провести урок — лекцию, с элементами беседы. Предварительно в устный счет включить задания на выделение квадрата двучлена из квадратного трехчлена. После вывода формулы, все выкладки оставить на доске и еще раз обратить внимание ребят на основные моменты вывода формулы. Формула нахождения дискриминанта и формулы нахождения корней квадратного уравнения должны быть вывешены на доске. Учителю необходимо показать, как правильно оформлять решение заданий, обратить внимание при нахождении корней квадратного уравнения, на знак у «-b». Желательно вывести формулу и показать, как ей правильно пользоваться, где в квадратном уравнении число «b» — четное.

Основное внимание следует уделять решению уравнений вида: ax 2 + bx + c = 0, где a ? 0, по формуле корней. Для вывода формулы достаточно рассмотреть один пример решения квадратного уравнения с помощью выделения квадрата двучлена из квадратного трехчлена, на котором разъясняется прием, используемый затем при выводе формулы в общем виде. Заниматься, специально решением квадратных уравнений с помощью выделения квадрата двучлена не следует. Рекомендуется ознакомить учащихся с формулами Виета, выражающими зависимость между корнями квадратного уравнения и его коэффициентами. Однако надо помнить, что этот материал носит вспомогательный характер. Доказательство соответствующей теоремы и обратной ей, а также решение задач с помощью формул Виета не относятся к обязательному материалу. Также рассматриваются дробно — рациональные уравнения, на которые мы и будем уделять внимание. Изучение данной темы позволяет существенно расширить аппарат уравнений, используемый для решения текстовых задач.

Таким образом, мы рассмотрели специфику изучения данной темы по разным учебным пособиям и выяснили, что авторы по — разному предлагают изучение темы «Квадратного трехчлена». И существенное различие в том, что эта тема изучается по учебнику А. Г. Мордковича в 8 классе, а по учебнику под редакцией Ю.Н. Макарычева, эта тема изучается в 9 классе.

Таким образом, можно сказать, что методика изучения квадратного трехчлена разнообразна, так как я, рассмотрев методику изучения по двум учебным пособиям, выяснила, что разные авторы по-разному предлагают методику изучения этой темы. Например, А. Г. Мордкович предлагает изучение темы: «Квадратный трехчлен» в 8 классе, а Ю.Н. Макарычев предлагает эту тему в 9 классе, но главное, что я хочу отметить, это то, что этой теме оба автора отводят не маловажное значение.

При рассмотрении данной темы: «Квадратный трехчлен», я использовала различные подходы к изучению данной темы, рассмотрела связь между квадратным трехчленом и квадратичной функции, откуда вытекает связь между квадратным трехчленом и квадратным уравнением, квадратными неравенствами.

Таким образом, можно сказать, что квадратный трехчлен является неотъемлемой частью курса алгебры, а также на этом материале строится дальнейшее изучение курса математики в школе, техникуме и ВУЗе. Изучение данной темы необходимо, так как решение различных заданий на данные темы способствует развитию логического мышления, что ведет за собой и развитие ребенка в целом.

Но также, я рассмотрела и методику изучения квадратного трехчлена в основной общеобразовательной школе, по двум учебным пособиям: учебник под редакцией А. Г. Мордкович, и учебник под редакцией Ю.Н. Макарычева, где выяснила, что методика изучения квадратного трехчлена разнообразна, так как разные авторы по- разному предлагают методику изучения этой темы. Например, А. Г. Мордкович предлагает изучение этой темы в 8 классе, а Ю.Н. Макарычев — в 9 классе, но главное, что я хочу отметить, это то, что этой теме оба автора отводят не маловажное значение.

Таким образом, при решении квадратного трехчлена происходит формирование таких качеств личности, как трудолюбие, целеустремленность, сила воли и точность. Поэтому в школах необходимо уделять внимание решению квадратного трехчлена. Также в своей курсовой работе, я предлагаю примеры конспектов урока.

1. Башмаков М.И. Квадратичная функция. — М., 1976. — 96 с.

. Выготский М.Я. Справочник по элементарной математике. — М.:Физматиз, 1951. — 390с.

. Горнштейн П.И., Полонский Б.И. Алгебра и элементарные функции. — М., Илекса; Харьков: Гимназия, 1998. — 60 с.

. Киейн Ф. Элементарная математика с точки зрения высшей. — М, 1978. -50 с.

. Крамор B.C. Повторяем и систематизируем школьный курс алгебры и начала анализа.// Просвещение. — М., 1993. — 415 с.

. Курош А.Г. Курс высшей алгебры. — М, 1992. — 550 с.

. Маденов П.С. Сборник задач по специальному курсу элементарной математики. -М.: Советская наука, 1987.-354 с.

. Никлоровский В.А. в мире уравнений. — М., 1987. — 170 с.

. Новоселов СИ. Специальный курс элементарной алгебры. — М, 1990. -223 с.

. Ю.Пичурин Л.Ф. за страницами учебника алгебры. — М., 1990. — 223 с. 11.

. Пособие по математике для поступающих в вузы: Учеб. Пособие/ Кутасов А.Д., Птолкина Т.С. и др. — М. Наука. 1988. -720 с 12.

. Савин А.П. Энциклопедический словарь юного математика. — М, 1990.-347 с.

. Сойер У. путь в современную математику. — М., 1972. — 200 с. 14.

. Справочник по высшей математике./сост. М.Я. Выгодский. — М., 1975.-872 с. 15.

. Справочник по методам решения задач по математике./Цынкин А.Г., Пинский а.И.; под ред. Шароватовой Т.В. — М.,1989.-576с.

. Стойлова Л.П. Математика.// Академия. — М, 2002. — 424

. Учебно — тренировочные материалы для подготовки к единому государственному экзамену. Математика./ Денищева Л.О., Глазков Ю.А. и др. — М., Ителлект — Центр, 2003.- 128 с.

. Шарыгин И.Ф. Факультативный курс по математике. Решение задач. — М., 1989. — 352 с.

. Шахно К.У. Справочник по математике. -3-е изд., испр и доп.// Высшая школа. — Минск, 1987. — 336 с.

. Уравнения с параметрами / Шестаков С.А., Юрченко Е.В. и др. -М., Слог, 1993. — 52 с.

.Энциклопедия элементарной математики.// Гостехиздат. — М., 1984.-600 с.

Теги: Методические особенности изучения квадратного трехчлена на уроках алгебры в 7-9 классах Диплом Педагогика

Видео:Решение биквадратных уравнений. 8 класс.Скачать

Курсовая работа: Формирование умения решения квадратных уравнений в 8 классе

ГОУ СПО «Кунгурское педагогическое училище»

Формирование умения решения квадратных уравнений в 8 классе

Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Курсовая работа

по методике математики

Глава 1. Теоретические аспекты обучению решения уравнений в 8 классе

1.1. Из истории возникновения квадратных уравнений 6

1.2. Основные направления изучения линий уравнений в школьном курсе алгебры 12

1.3. Методика изучения квадратных уравнений 15

Глава 2. Методико-педагогические основы обучения решению квадратных уравнений

2.1. Урок – лекция по теме «Формула корней квадратного уравнения с четным вторым коэффициентом» 23

2.2. Урок – практикум по теме «Квадратные уравнения» 28

2.3. Обобщающий урок по теме «Квадратные уравнения» в форме игры «Звездный час» 32

Список литературы 38

Сухие строки уравнений –

В них сила разума влилась.

В них объяснение явлений,

Вещей разгаданная связь.

Уравнения в школьном курсе алгебры занимают ведущее место. На их изучение отводится времени больше, чем на любую другую тему школьного курса математики. Сила теории уравнений в том, что она не только имеет теоретическое значение для познания естественных законов, но и служит конкретным практическим целям. Большинство задач о пространственных формах и количественных отношениях реального мира сводится к решению различных видов уравнений. Овладевая способами их решения, люди находят ответы на различные вопросы из науки и техники (транспорт, сельское хозяйство, промышленность, связь и т. д.). Так же для формирования умения решать уравнения большое значение имеет самостоятельная работа учащегося при обучении решения уравнений. При изучении любой темы уравнения могут быть использованы как эффективное средство закрепления, углубления, повторения и расширения теоретических знаний, для развития творческой математической деятельности учащихся.[10,241].

Автором данной работы выбрана тема «Формирование умения решения квадратных уравнений в 8 классе», так как она актуальна в современном мире; это объясняется тем, что уравнения широко используются в различных разделах математики, в решении важных прикладных задач.

Для этой темы характерна большая глубина изложения и богатство устанавливаемых с ее помощью связей в обучении, логическая обоснованность изложения. Поэтому она занимает исключительное положение в линии уравнений. К изучению темы «Квадратные уравнения» учащиеся приступают, уже накопив определенный опыт, владея достаточно большим запасом алгебраических и общематематических представлений, понятий, умений. В значительной мере именно на материале данной темы осуществляется синтез материала, относящегося к уравнениям.

Исходя из вышесказанного, автор, выбирая тему курсовой работы, руководствовался ее значимостью и сложностью при обучении учащихся решению квадратных уравнений разного вида.

Цель работы: формирование представлений о работе над квадратными уравнениями на уроках математики. Исходя из данной цели, были поставлены следующие задачи:

· изучить научно-методическую литературу, касающуюся изучению уравнений;

· проанализировать школьные учебники и выделить в них место уравнений.

· разработать уроки по данной теме.

Для решения вышеуказанных задач были изучены следующие литературные источники:

1) Алгебра: Учеб. для 8 кл. общеобразоват. учреждений / С.М. Никольский, М.К. Потапов и др. – 2-е изд. – М.: Просвещение, 2003. – 287 с.

2) Алгебра: Учеб. для 8 кл. общеобразоват. учреждений / Ш.А.Алимов, Ю.М.Колягин, Ю.В.Сидоров и др. – 10-е изд. – М.: Просвещение, 2003. – 255с.

3) Мордкович А.Г.. Алгебра: учеб. для 8 кл. общеобразоват. учреждений. – М.: Просвещение, 2004. – 287с.

4) Бекаревич А.Б. Уравнения в школьном курсе математики. – М., 2000. – 241с.

5) Глейзер Г.И. История математики в школе VII – VIII классы. – М., 1982.

6) Колягин Ю.М. Методика преподавания математике в средней школе. Частные методики. – М.: Просвещение, 2002.

7) Маркушевич Л.А. Уравнения и неравенства в заключительном повторении курса алгебры средней школы // Математика в школе. – 2001. — №1. – с.15

8) Методика и технология обучения математике. Курс лекций: пособие для вузов / под ред. Н.Л.Стефановой, Н.С. Подходовой. – М.: Дрофа, 2005. – 416 с.

9) Мишин В.И. Методика преподавания математики в средней школе. – М.,1999.- 398с.

10) Оганесян В.А. Методика преподавания математики в средней школе. – М.: Просвещение, 2003. – 368 с.

Проанализировав некоторые источники, можно сделать вывод о недостаточном освещении изучаемого вопроса в современной методической литературе.

Объект исследования работы: процесс обучения математике.

Предмет: формирование умения решения квадратных уравнений у учащихся 8-го класса.

Контингент: учащиеся 8-го класса.

Глава 1. Теоретические аспекты обучению решения уравнений в 8 классе

1.1. Из истории возникновения квадратных уравнений

Алгебра возникла в связи с решением разнообразных задач при помощи уравнений. Обычно в задачах требуется найти одну или несколько неизвестных, зная при этом результаты некоторых действий, произведенных над искомыми и данными величинами. Такие задачи сводятся к решению одного или системы нескольких уравнений, к нахождению искомых с помощью алгебраических действий над данными величинами. В алгебре изучаются общие свойства действий над величинами.

Некоторые алгебраические приемы решения линейных и квадратных уравнений были известны еще 4000 лет назад в Древнем Вавилоне.

Квадратные уравнения в Древнем Вавилоне

Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до нашей эры вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения:

Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены. Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.

В «Арифметике» Диофанта нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней.

При составлении уравнений Диофант для упрощения решения умело выбирает неизвестные.

Вот, к примеру, одна из его задач.

Задача 2. «Найти два числа, зная, что их сумма равна 20, а произведение — 96».

Диофант рассуждает следующим образом: из условия задачи вытекает, что искомые числа не равны, так как если бы они были равны, то их произведение равнялось бы не 96, а 100. Таким образом, одно из них будет больше половины их суммы, т. е. 10 + х. Другое же меньше, т. е. 10 — х. Разность между ними 2х. Отсюда уравнение:

Отсюда х = 2. Одно из искомых чисел равно 12, другое 8. Решение х = — 2 для Диофанта не существует, так как греческая математика знала только положительные числа.

Если решить эту задачу, выбирая в качестве неизвестного одно из искомых чисел, то можно прийти к решению уравнения:

Ясно, что, выбирая в качестве неизвестного полуразность искомых чисел, Диофант упрощает решение; ему удается свести задачу к решению неполного квадратного уравнения.

Квадратные уравнения в Индии

Задачи на квадратные уравнения встречаются уже в астрономическом трактате «Ариабхаттиам», составленном в 499 г. индийским математиком и астрономом Ариабхаттой. Другой индийский ученый, Брахмагупта (VII в.), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме:

ax 2 + bх = с, а> 0. (1)

В уравнении (1) коэффициенты, могут быть и отрицательными. Правило Брахмагупты по существу совпадает с нашим.

В Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу в народных собраниях, предлагая и решая алгебраические задачи». Задачи часто облекались в стихотворную форму.

Вот одна из задач знаменитого индийского математика XII в. Бхаскары.

Решение Бхаскары свидетельствует о том, что автор знал о двузначности корней квадратных уравнений.

Соответствующее задаче 3 уравнение:

,

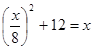
Бхаскара пишет под видом:

x 2 — 64x = — 768

и, чтобы дополнить левую часть этого уравнения до квадрата, прибавляет к обеим частям 32 2 , получая затем:

x 2 — б4х + 32 2 = -768 + 1024,

Квадратные уравнения у Аль-Хорезми

В алгебраическом трактате Аль-Хорезми дается классификация линейных и квадратных уравнений. Автор насчитывает 6 видов уравнений, выражая их следующим образом:

1) «Квадраты равны корням», т. е. ах 2 = bх.

2) «Квадраты равны числу», т. е. ах 2 = с.

3) «Корни равны числу», т. е. ах = с.

4) «Квадраты и числа равны корням», т. е. ах 2 + с = bх.

5) «Квадраты и корни равны числу», т. е. ах 2 + bх =с.

6) «Корни и числа равны квадратам», т. е. bх + с == ах 2 .

Для Аль-Хорезми, избегавшего употребления отрицательных чисел, члены каждого из этих уравнений слагаемые, а не вычитаемые. При этом заведомо не берутся во внимание уравнения, у которых нет положительных решений. Автор излагает способы решения указанных уравнений, пользуясь приемами ал-джабр и ал-мукабала. Его решение, конечно, не совпадает полностью с нашим. Уже не говоря о том, что оно чисто риторическое, следует отметить, например, что при решении неполного квадратного уравнения первого вида Аль-Хорезми, как и все математики до XVII в., не учитывает нулевого решения, вероятно, потому, что в конкретных практических задачах оно не имеет значения. При решении полных квадратных уравнений Аль-Хорезми на частных числовых примерах излагает правила решения, а затем их геометрические доказательства.

Задача 4. «Квадрат и число 21 равны 10 корням. Найти корень» (подразумевается корень уравнения х 2 + 21 = 10х).

Решение: раздели пополам число корней, получишь 5, умножь 5 само на себя, от произведения отними 21, останется 4. Извлеки корень из 4, получишь 2. Отними 2 от 5, получишь 3, это и будет искомый корень. Или же прибавь 2 к 5, что даст 7, это тоже есть корень.

Трактат Аль-Хорезми является первой, дошедшей до нас книгой, в которой систематически изложена классификация квадратных уравнений и даны формулы их решения.[3,75]

Квадратные уравнения в Европе XII — XVII в.

Формы решения квадратных уравнений по образцу Аль-Хорезми в Европе были впервые изложены в «Книге абака», написанной в 1202г. итальянским математиком Леонардом Фибоначчи. Автор разработал самостоятельно некоторые новые алгебраические примеры решения задач и первый в Европе подошел к введению отрицательных чисел.

Эта книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из этой книги переходили почти во все европейские учебники XIV-XVII вв. Общее правило решения квадратных уравнений, приведенных к единому каноническому виду x 2 + bх = с при всевозможных комбинациях знаков и коэффициентов b, c, было сформулировано в Европе в 1544 г. М.Штифелем.

Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли среди первых вXVI в. учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.[5,12].

Истоки алгебраических методов решения практических задач связаны с наукой древнего мира. Как известно из истории математики, значительная часть задач математического характера, решаемых египетскими, шумерскими, вавилонскими писцами-вычислителями (XX—VI вв. до н. э.), имела расчетный характер. Однако уже тогда время от времени возникали задачи, в которых искомое значение величины задавалось некоторыми косвенными условиями, требующими, с нашей современной точки зрения, составления уравнения или системы уравнений. Первоначально для решения таких задач применялись арифметические методы. В дальнейшем начали формироваться начатки алгебраических представлений. Например, вавилонские вычислители умели решать задачи, сводящиеся с точки зрения современной классификации к уравнениям второй степени. Был создан метод решения текстовых задач, послуживший в дальнейшем основой для выделения алгебраического компонента и его независимого изучения.

Это изучение осуществлялось уже в другую эпоху сначала арабскими математиками (VI—Х вв. н. э.), выделившими характерные действия, посредством которых уравнения приводились к стандартному виду приведение подобных членов, перенос членов из одной части уравнения в другую с переменой знака. А затем европейскими математиками Возрождения, в итоге длительного поиска создавшими язык современной алгебры, использование букв, введение символов арифметических операций, скобок и т. д. На рубеже XVI—XVII вв. алгебра как специфическая часть математики, обладающая своим предметом, методом, областями приложения, была уже сформирована. Дальнейшее ее развитие, вплоть до нашего времени, состояло в совершенствовании методов, расширении области приложений, уточнении понятий и связей их с понятиями других разделов математики.

Итак, ввиду важности и обширности материала, связанного с понятием уравнения, его изучение в современной методике математики связано с тремя главными областями своего возникновения и функционирования.

1.2. Основные направления изучения линий уравнений в школьном курсе алгебры

Уравнение как общематематическое понятие многоаспектно. Можно выделить главные области возникновения и функционирования понятия «уравнение» как:

· средства решения текстовых задач;

· особого рода формулы, служащей в алгебре объектом изучения;

· формулы, которой косвенно определяются числа или координаты точек плоскости (пространства), служащие его решением.[12,268]

Каждое из этих представлений оказалось в том или ином отношении полезным.

Названным областям относятся три основных направления изучения линий уравнений в школьном курсе алгебры.

1. Прикладная направленность линии уравнений раскрывается главным образом при изучении алгебраического метода решения текстовых задач. Этот метод широко применяется в школьной математике, поскольку он связан с обучением приемам, используемым в приложениях математики.

В настоящее время, ведущее положение в приложениях математики занимает математическое моделирование (Математическое моделирование заключается в конструировании по определенным правилам некоторой формальной системы, которая отображает через совокупность математических операций над величинами определенную гипотезу о структуре или воспитания). Используя это понятие, можно сказать, что прикладное значение уравнений, их систем определяется тем, что они являются основной частью математических средств, используемых в математическом моделировании. [14,246].

2. Теоретико-математическая направленность линии уравнений раскрывается в двух аспектах:

· выделение и изучение наиболее важных классов уравнений, и их систем;

· изучение обобщенных понятий, относящихся ко всей линии в целом.

Оба эти аспекта необходимы в курсе школьной математики. Основные классы уравнений связаны с простейшими и одновременно наиболее важными математическими моделями. Использование обобщенных понятий и методов позволяет логически упорядочить изучение линии в целом, поскольку они описывают то общее, что имеется в процедурах и приемах решения, относящихся к отдельным классам уравнений, неравенств, систем. В свою очередь, эти общие понятия и методы опираются на основные логические понятия: неизвестное, равенство, равносильность, логическое следование, которые также должны быть раскрыты в линии уравнений.

3. Направленность на установление связей с остальным содержанием курса математики. Эта линия тесно связана с числовой линией, причем эта связь — двусторонняя. Основная идея, реализуемая в процессе установления взаимосвязи этих линий,— это идея последовательного расширения числовой системы. Все числовые области, рассматриваемые в школьной алгебре и началах анализа, за исключением области всех действительных чисел, возникают в связи с решением каких-либо уравнений.

Например, введение арифметического квадратного корня из рациональных чисел позволяет записывать корни не только уравнений вида х 2 = b, где b—неотрицательное рациональное число, но и любых квадратных уравнений с рациональными коэффициентами и неотрицательным дискриминантом.[9,341]

Линия уравнений тесно связана также и с функциональной линией. Одна из важнейших таких связей — приложения методов, разрабатываемых в линии уравнений, к исследованию функции (например, к заданиям на нахождение области определения некоторых функций, их корней, промежутков знакопостоянства и т. д.). С другой стороны, функциональная линия оказывает существенное влияние как на содержание линии уравнений , так и на стиль ее изучения. В частности, функциональные представления служат основой привлечения графической наглядности к решению и исследованию уравнений и их систем.[12,269]

Изучение и использование преобразований уравнений и их систем, с одной стороны, предполагают достаточно высокую логическую культуру учащихся, а с другой стороны, в процессе изучения и применения таких преобразований имеются широкие возможности для формирования логической культуры.

Таким образом, владение содержанием линии уравнений позволяет расширить список выполнимых преобразований. Так, умение решать квадратные уравнения позволяет осуществлять сокращение дробей, в числителе или знаменателе которых имеется квадратный трехчлен. В итоге изучения материала линии уравнений учащиеся должны не только овладеть применением алгоритмических предписаний к решению конкретных заданий, но и научиться использовать логические средства для обоснования решений в случаях, когда это необходимо.

1.3. Методика изучения квадратных уравнений

С началом изучения систематического курса алгебры основное внимание уделяется способам решения квадратных уравнений, которые становятся специальным объектом изучения. Для этой темы характерна большая глубина изложения и богатство устанавливаемых с ее помощью связей в обучении, логическая обоснованность изложения. Поэтому она занимает исключительное положение в линии уравнений и неравенств. К изучению этой темы учащиеся приступают, уже накопив определенный опыт, владея достаточно большим запасом алгебраических и общематематических представлений, понятий, умений.

Умение решать квадратные уравнения служит базой для решения других уравнений и их систем (дробных рациональных, иррациональных, высших степеней).

Для того чтобы решить любое квадратное уравнение, учащиеся должны знать:

· формулу нахождения дискриминанта;

· формулу нахождения корней квадратного уравнения;

· алгоритмы решения уравнений данного вида.

· решать неполные квадратные уравнения;

· решать полные квадратные уравнения;

· решать приведенные квадратные уравнения;

· находить ошибки в решенных уравнениях и исправлять их;

Решение каждого уравнения складывается из двух основных частей:

· преобразования данного уравнения к простейшим;

· решения уравнений по известным правилам, формулам или алгоритмам.

При изучении темы «Квадратные уравнения» рассматриваются неполные, полные и приведенные квадратные уравнения. Для изучения данной темы были проанализированы современные школьные учебники разных авторов, таких как А.Г.Мордкович, С.М.Никольский, Ю.Н.Макарычев, М.И.Башмаков.

Видео:Быстрый способ решения квадратного уравненияСкачать

Реферат «Решение квадратных уравнений различными способами.»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Муниципальное общеобразовательное учреждение

Средняя общеобразовательная школа № 1

Тема:Решение квадратных уравнений различными способами.

Выполнила: Ученица 8 Б класса

Пешкова Оксана Ильинична

Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Оглавление

Видео:Алгебра 8 класс (Урок№29 - Решение задач с помощью квадратных уравнений.)Скачать

Аннотация

Предметисследования: способы решения квадратных уравнений.

Цель: Изучить теоретические основы квадратных уравнений и способов их решении; рассмотреть применение данных способов решения квадратных уравнений на конкретных примерах.

1) Произвести анализ учебно–методической литературы по решению квадратных уравнений.

2) Произвести анализ различных способов решения квадратных уравнений

3)Изучить историю развития квадратных уравнений.

4) Изучить различные способы решения квадратных уравнений и апробировать материал на практике.

Гипотеза: любое квадратное уравнение можно решить всеми существующими способами

Обоснование: Уравнения — это наиболее объёмная тема всего курса математики. Данная работа является попыткой обобщить и систематизировать изученный материал по выше указанной теме. В него вошли как известные нам из школьного курса алгебры способы решения квадратных уравнений, так и дополнительный материал.

Теоретические методы: изучение литературы по теме исследования

Анализ информации, полученной при изучении литературы; анализ результатов, получены при решении квадратных уравнений различными способами.

Сравнение способов на рациональность их использования при решении квадратных уравнений.

Видео:Математика| Разложение квадратного трехчлена на множители.Скачать

I .Введение

Уравнения в школьном курсе алгебры занимают ведущее место. На их изучение отводится времени больше, чем на любую другую тему. Действительно, уравнения не только имеют важное теоретическое значение, но и служат чисто практическим целям. Подавляющее число задач о пространственных формах и количественных отношениях реального мира сводится к решению различных видов уравнений. Овладевая способами их решения, мы находим ответы на различные вопросы из науки и техники (транспорт, сельское хозяйство, промышленность, связь и т. д.).

Выбор этой темы основывался на том, что уравнения есть как в программе начальной, так и в каждом последующем классе общеобразовательных школ, лицеев, колледжей. Многие геометрические задачи, задачи по физике, химии и биологии решаются с помощью уравнений. Уравнения решали двадцать пять веков назад. Они создаются и сегодня – как для использования в учебном процессе, так и для конкурсных экзаменов в вузы, для олимпиад самого высокого уровня.

Квадратное уравнение представляет собой большой и важный класс уравнений, решающих как с помощью формул, так и с помощью элементарных функций.

В учебниках мы знакомимся с несколькими видами квадратных уравнений, и отрабатываем решение по формулам. Вместе с тем, современные научно – методические исследования показывают, что использование разнообразных методов и способов позволяет значительно повысить эффективность и качество изучения решений квадратных уравнений.

Выбор способа должен оставаться за учащимся. Каждый ученик должен уметь верно и рационально решать квадратные уравнения. Так как в некоторых случаях можно их решать устно, только для этого необходимо помнить алгоритм решения квадратных уравнений, который может пригодиться на экзамене ЕГЭ, при поступлении в ВУЗы и различных жизненных ситуациях.

Квадратное уравнение-это фундамент, на котором покоится величественное здание алгебры.

С помощью формул корней квадратных уравнений можно решить любые квадратные уравнения. Однако имеются и другие способы решения квадратных уравнений, которые позволяют очень быстро и рационально решать многие уравнения.

Таким образом возникает необходимость изучения этих дополнительных способов решения. Все сказанное выше определяет актуальность темы выполненной работы.

Видео:ТЕОРЕМА ВИЕТА ЗА 2 МИНУТЫСкачать

II . Определение квадратного уравнения, его виды.

Определение:Квадратным уравнением называется уравнение вида

гдех-переменная, а, b и с-некоторые числа, причем,а≠0.

Если в квадратном уравнении ах 2 + bx + c =0 хотя бы один из коэффициентов b или с равен нулю, то такое уравнение называют неполным квадратным уравнением.

Неполные квадратные уравнения бывают трёх видов:

1)ах 2 +с=0, где с ≠ 0;

2) ах 2 + b х = 0, где b ≠ 0;

Квадратные уравнения  это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных и трансцендентных уравнений и неравенств.

Видео:Математика это не ИсламСкачать

III . Из истории квадратных уравнений.

Видео:Метод выделения полного квадрата. 8 класс.Скачать

1) Квадратные уравнения в Древнем Вавилоне

Необходимость решать уравнения не только первой, но и второй степени ещё в древности была вызвана потребностью решать задачи, связанные нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до н.э. вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения:

х 2 + х = , х 2 – х = 14

Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены.

Видео:Метод переброски при решении квадратных уравненийСкачать

2) Квадратные уравнения в Индии.

Задачи на квадратные уравнения встречаются уже в астрономическом тракте «Ариабхаттиам», составленном в 499 г. индийским математиком и астрономом Ариабахаттой. Другой индийский ученый, Брахмагупта ( VII в.), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме:

В уравнении коэффициенты, кромеа, могут быть отрицательными. Правило Брахмагупта по существу совпадает с нашим.

Видео:Методы решения квадратных уравненийСкачать

3) Квадратные уравнения в Европе XIII — XVII вв.

Формулы решения квадратных уравнений по образцу ал-Хорезми в Европе были впервые изложены в «Книге абака», написанной в 1202 г. Итальянским математиком Леонардо Фибоначчи. Этот объемный труд, в котором отражено влияние математики как стран ислама, так и Древней Греции, отличается и полнотой, и ясностью изложения. Автор разработал самостоятельно некоторые новые алгебраические примеры решения задач и первый в Европе подошел к введению отрицательных чисел. Его книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из «Книги абака» переходили почти во все европейские учебники XVI — XVII вв. и частично XVIII .

Общее правило решения квадратных уравнений, приведенных к единому каноническому виду х 2 + b х = с, при всевозможных комбинациях знаков коэффициентов b , с было сформулировано в Европе лишь в 1544 г. М.Штифелем.

Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в XVI в. Учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.

Видео:Неполные квадратные уравнения. Алгебра, 8 классСкачать

IV . Различные способы решения квадратных уравнений.

В школьном курсе математике изучают формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения. Однако имеются и другие способы решения квадратных уравнений, которые позволяют очень быстро и рационально решать многие уравнения. Имеется десять способов решения квадратных уравнений. Подробно разберем каждые из них.

1) Разложение левой части уравнения на множители .

1. Решим уравнение х 2 + 10х – 24 = 0.

Разложим левую часть уравнения на множители:

х 2 + 10х – 24 = х 2 + 12х – 2х – 24 = х (х + 12) – 2 (х +12) = (х + 12)(х – 2).

Следовательно, уравнение можно переписать так:

Так как произведение равно нулю, то по крайне мере один из его множителей равен нулю. Поэтому левая часть уравнения обращается в нуль при х = 2, а также при х = — 12. это означает, что числа 2 и – 12 являются корнями уравнения х 2 + 10х – 24 = 0.

Видео:Метод переброски в квадратных уравнениях. ЕГЭ и ОГЭ 2022 по математикеСкачать

2) Метод выделения полного квадрата

Поясним этот метод на примере.

Решим уравнение х 2 + 6х – 7 = 0

Выделим в левой части полный квадрат. Для этого запишем выражение

х 2 + 6х в следующем виде:

х 2 + 6х = х 2 + 2· х ·3.

В полученном выражении первое слагаемое – квадрат числа х, а второе – удвоенное произведение х на 3. поэтому чтобы получить полный квадрат, нужно прибавить 3 2 , так как

х 2 + 2· х ·3 + 3 2 = (х + 3) 2 .

Преобразуем теперь левую часть уравнения

прибавляя к ней и вычитая 3 2. Имеем:

х 2 + 6х – 7= х 2 + 2· х ·3 + 3 2 – 3 2 – 7= (х + 3) 2 – 9– 7= (х + 3) 2 – 16.

Таким образом, данное уравнение можно записать так:

(х + 3) 2 –16 = 0, т.е. (х + 3) 2 = 16.

Следовательно, х=3=4,х₁=1, или х +3= — 4 , х₂ = – 7.

Видео:Метод переброскиСкачать

3) Решение квадратных уравнений по формуле

Умножим обе части уравнения

ах 2 + b х + с = 0, а ≠ 0,на 4а и следовательно имеем:

4а 2 х 2 + 4а b с + 4ас = 0.

((2ах) 2 + 2ах · b + b 2 ) – b 2 + 4ас = 0,

(2ах + b ) 2 = b 2 – 4ас,

а) 4х 2 + 7х + 3 = 0.

а = 4, b = 7, с = 3, D = b 2 – 4ас = 7 2 – 4· 4 ·3 = 49 – 48 = 1, D >два разных корня;

х = , х = ; х = , х₁ = , х = , х₂ = –1

Таким образом, в случае положительного дискриминанта,т. е. при b 2 – 4ас≥0 уравнение ах 2 + b х + с = 0 имеет два различных корня.

б) 4х 2 – 4х + 1 = 0,

Итак, если дискриминант равен нулю, т. е. = b 2 – 4ас= 0, тоуравнение ах 2 + b х + с = 0 имеет единственный корень, х =

в) 2х 2 +3х + 4 = 0, а =2, b = 3, с = 4, D = b 2 – 4ас= 9 – 4∙2∙4 =9 – 32 = — 13,

Итак, если дискриминант отрицателен, т. е. = b 2 – 4ас

Видео:Формула корней квадратного уравнения. Алгебра, 8 классСкачать

4) Решение уравнений с использованием теоремы Виета(прямой и обратной)

а) Как известно, приведенное квадратное уравнение имеет вид

Его корни удовлетворяют теореме Виета, которая приа = 1 имеет вид

Отсюда можно сделать следующие выводы (по коэффициентам p и q можно предсказать знаки корней).

а) Если свободный член q приведенного уравнения (1) положителен ( q >0), то уравнение имеет два одинаковых по знаку корня и это зависит от второго коэффициента p .

Если p >0, то оба корня отрицательные, если p

х 2 – 3х + 2 = 0; х₁ = 2 и х₂ = 1, так как q = 2>0 и p = – 3

х 2 +8х + 7 = 0; х₁ = – 7 и х₂ = – 1, так как q = 7 > 0 и p = 8 >0.

б) Если свободный член q приведенного уравнения (1) отрицателен ( q p p >0.

х 2 + 4х – 5 = 0; х₁ = – 5 и х₂ = 1, так как q = – 5 p = 4 > 0;

х 2 – 8х – 9 = 0; х₁ = 9 и х₂ = – 1, так как q = – 9 p = – 8 >0.

б) Теорема Виета для квадратного уравнения

Справедлива теорема, обратная теореме Виета:

Если числа х₁ и х₂ таковы, что х₁+х₂ = -р, х₁х₂ = q , то х₁ и х₂ – корни квадратного уравнения

Эта теорема позволяет в ряде случаев находить корни квадратного уравнения без использования формулы корней.

1. Решить уравнение: х 2 – 9х + 14 =0

Попробуем найти два числа х₁ и х₂ , такие, что

Такими числами являются 2 и 7. По теореме, обратной теореме Виета, они и служат корнями заданного квадратного уравнения.

2. Решить уравнение: х 2 +3х – 28 = 0

Попробуем найти два числа х₁ и х₂ , такие, что

Нетрудно заметить, что такими числами будут – 7 и 4. Они и являются корнями заданного уравнения.

Видео:Как решать квадратные уравнения без дискриминантаСкачать

5)Решение уравнений способом «переброски»

Рассмотрим квадратное уравнение

Умножая обе его части на а, получаем уравнение

Пусть ах= у, откуда х = ; тогда приходим к уравнению

равносильного данному. Его корни у₁ и у₂ найдем с помощью теоремы Виета. Окончательно получаем х₁= и х₁ = . При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его и называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.

Решим уравнение 2х 2 – 11х + 15 = 0.

Решение. «Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение

Согласно теореме Виета

Видео:Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать

6)Свойства коэффициентов квадратного уравнения.

А. Пусть дано квадратное уравнение

1.Если а+ b +с=0 (т.е. сумма коэффициентов уравнения равна нулю),то х₁ =1, х₂= .Доказательство. Разделим обе части уравнения на а ≠ 0, получим приведенное квадратное уравнение

Согласно теореме Виета

По условиюа + b + с = 0, откуда b = – а – с. Значит,

Получаем х₁=1, х₂=, что и требовалось доказать.

Доказательство. По теореме Виета

По условию а – b + с = 0, откуда b = а + с. Таким образом,

т.е. х₁= – 1 и х₂ = , что и требовалось доказать.

1. Решим уравнение 345х 2 –137х – 208 = 0.

Решение. Так как а + b + с = 0 (345 – 137 – 208 = 0), то х₁=1, х₂= = .

2. Решим уравнение 132х 2 + 247х + 115 = 0

Решение. Т. к. а- b +с = 0 (132 – 247 +115=0), то

Б. Если второй коэффициент b = 2 k – четное число, то формулу корней

можно записать в виде

Решим уравнение 3х 2 –14х + 16 = 0.

D = k 2 – ac = (– 7) 2 – 3 · 16 = 49 – 48 = 1, D >0, два различных корня;

В. Приведенное уравнение

совпадает с уравнением общего вида, в которома = 1, p и c = q . Поэтому для приведенного квадратного уравнения формула корней

Формулу (3) особенно удобно использовать, когда p – четное число.

1. Решим уравнение х 2 –14х – 15 = 0.

Видео:Встреча с Путиным в общежитии МГУ на Воробьевых горах!Скачать

7)Графическое решение квадратного уравнения

Если в уравнении x 2 + px + q = 0перенести второй и третий члены в правую часть, то получим x 2 = – px – q .

Построим графики зависимостей у = х 2 и у = – px – q . (рис.1)

График первой зависимости – парабола,проходящая через начало координат.График второй зависимости – прямая.Возможны следующие случаи:прямая и парабола могут пересекаться в двух точках, абсциссыточек пересечения являются корнями квадратного уравнения;

— прямая и парабола могут касаться (только одна общая точка),т.е.уравнение имеет одно решение;

— прямая и парабола не имеют общих точек, т.е. квадратноеуравнение не имеет корней.

📸 Видео

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

5 способов решения уравнений | Эрик Легион | 100балльный репетиторСкачать