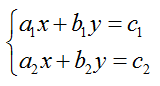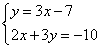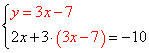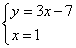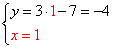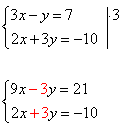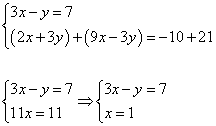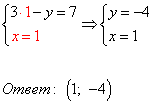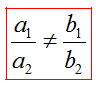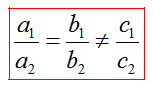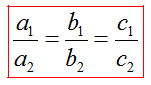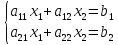Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Министерство образования Иркутской области
профессиональное образовательное учреждение
«Иркутский авиационный техникум»
по дисциплине «Математика»
Методическое пособие по теме «Линейная алгебра» выполнено для использования его студентами при самостоятельных занятиях по теме «Линейная алгебра» с целью углубления знаний по этой теме и отработки практических навыков решения систем n линейных уравнений с n неизвестными.
от «25» июня 2015 г.
Составитель: преподаватель ИАТ Сыровая И.С.
Методическое пособие по теме «Линейная алгебра» выполнено для использования его студентами при самостоятельных занятиях по теме «Линейная алгебра» с целью углубления знаний по этой теме и отработки практических навыков решения систем n линейных уравнений с n неизвестными.
Пособие состоит из 7 разделов.
В этом разделе даны определения матрицы, видов матриц и определителей
2-го и 3-го порядков., рассмотрены примеры их вычисления.
Приведена информация о системах линейных уравнений и их решении.
3. Решение систем линейных уравнений по формулам Крамера.
4. Решение систем линейных уравнений методом Гаусса.
5. Решение систем линейных уравнений в матричной форме.
6. Задания для самостоятельной работы.
1.1 ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
Матрицей размера m х n называется прямоугольная таблица чисел
,
содержащая m строк и n столбцов.
Каждый элемент матрицы аik имеет два индекса: i – номер строки и k – номер столбца.
Матрица называется квадратной порядка n , если она состоит из n строк и n столбцов.
Матрица размера 1хn называется матрицей-строкой , матрица размера m х 1 называется матрицей-столбцом .
Нулевой матрицей заданного размера называется матрица, все элементы которой равны нулю.
Треугольной матрицей n-го порядка называется квадратная матрица, все элементы которой, расположенные ниже главной диагонали, равны нулю:
.
Единичной называется квадратная матрица n-го порядка, у которой элементы главной диагонали равны 1, а все остальные элементы – нули:
.
Матрицы А = ( а ik ) m,n и В = ( в ik ) m,n называются РАВНЫМИ , если а ik = в ik (i = 1,…,m;
k = 1,…,n).
ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД МАТРИЦАМИ
Для любых матриц одинакового размера выполняются свойства:
1) А + В = В +А 2) А + (В + С) = (А + В) + С
Транспонированной для матрицы А называется матрица А Т , строки которой являются столбцами матрицы А, а столбцы – строками матрицы А.
Пример 1. Даны матрицы
и 
Построить матрицу С = 2А – 3В + А Т .
Решение:
— 
+
+ 
= 
.
1.3 УМНОЖЕНИЕ МАТРИЦ
размера m х n с элементами
Иными словами, для получения элемента, стоящего в i -ой строке результирующей матрицы и в k -ом ее столбце, следует вычислить сумму попарных произведений элементов
i -ой строки матрицы А на k -ый столбец матрицы В.
Пример 2. Найти произведение матрицы А на матрицу В:
.
Решение.
.
Число столбцов первой матрицы равно числу строк второй. Это – условие согласования матриц при умножении. Если оно нарушено, матрицы перемножить нельзя.
Определитель второго порядка.
Пусть матрица А – квадратная матрица 2-го порядка:
.
Определителем 2-го порядка (матрицы а) называется число
Пример . Вычислить определитель матрицы
Решение:
Определитель третьего порядка.
Пусть матрица А – квадратная матрица 3-го порядка:
Определителем 3-го порядка (матрицы А) называется число
Правило треугольника:
Пример . Вычислить определить
Разложение определителя по строке или столбцу.
Минором элемента aik называется определитель Мik, составленный из элементов, оставшихся после вычеркивания из матрицы А i-ой строки и k-го столбца.
Алгебраическим дополнением элемента aik называется число 
.
Определителем 3-го порядка (матрицы А) называется сумма произведений элементов первой строки матрицы на их алгебраические дополнения:
Данную формулу называют разложением определителя по первой строке.
Пример. Вычислить определитель матрицы
.
Решение . Находим миноры и алгебраические дополнения элементов 1-ой строки матрицы:
Вычисляем искомый определитель:
D(А) = 3 . 7 + (-2) . (-35) + 4 . (-7) = 63.
Свойства определителей.
1. Определитель не меняется при транспонировании, т.е. D(А Т ) = D (А).
2. Если две строки определителя поменять местами, то определитель меняет знак.
3. Если все элементы какой-либо строки (или столбца) равны нулю, то определитель равен нулю.
4. Если все элементы какой-либо строки (столбца) имеют общий множитель, то его можно вынести за знак определителя.
5. Если в определителе две строки (два столбца) одинаковы или пропорциональны, то определитель равен нулю.
6. Определитель не изменяется, если к элементам какой-либо строки (столбца) прибавить элементы другой строки (столбца), умноженные на одно и то же число.
Системы линейных уравнений
Система линейных уравнений с переменными x , y и z имеет вид:
Решением системы уравнений называется упорядоченная тройка чисел
x , y , z , являющаяся решением каждого уравнения системы.
Для системы уравнений можно составить матрицу А – матрицу коэффициентов при неизвестных и матрицу D – матрицу-столбец свободных коэффициентов.
a 1 b 1 c 1 d 1
Составим и вычислим определитель матрицы А:
a1 b1 c1
Решение систем линейных уравнений по формулам Крамера.
Теорема Крамера. Система n линейных уравнений с n неизвестными, определитель которой отличен от нуля, всегда имеет решение и притом единственное. Оно находится следующим образом: Значение каждого из неизвестных равно дроби, знаменатель которой равен главному определителю системы, а числитель получается из главного определителя путём замены столбца коэффициентов при искомом неизвестном на столбец свободных членов.
- Решение систем линейных уравнений различными методами
- Просмотр содержимого документа «Решение систем линейных уравнений различными методами»
- МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ДЛЯ СТУДЕНТОВ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОГО ЗАНЯТИЯ «Решение систем линейных уравнений» учебно-методический материал по математике на тему
- Скачать:
- Предварительный просмотр:
- По теме: методические разработки, презентации и конспекты
- 🌟 Видео
Для системы (1) запишем определители ∆, ∆ x , ∆ y , ∆ z .
a1 b1 c1 d1 b1 c1 a1 d1 c1
a1 b1 d1
По формулам Крамера: x = ∆ x / ∆ y = ∆ y / ∆ z = ∆ z / ∆
Пример: x – y + 3 z = 3
Вычислим главный определитель системы:
∆ = 3 1 – 1 = 1 + 2 – 63 –6 –7 + 3 = –70
Заменив столбец коэффициентов при переменной x столбцом свободных коэффициентов, получим определитель ∆ x :
∆ х = 17 1 –1 = 3 – 4 – 357 + 12 – 21 + 17 = –350
Заменив столбец коэффициентов при переменной y столбцом свободных коэффициентов, получим определитель ∆ y :
∆ y = 3 17 –1 = 17 – 6 – 36 – 102 – 9 – 4 = –140
Заменив столбец коэффициентов при переменной z столбцом свободных коэффициентов, получим определитель ∆ z :
∆ z = 3 1 17 = –4 – 34 – 63 – 6 + 119 – 12 = 0
По формулам Крамера вычислим значения x , y и z :
Решение систем методом Гаусса.
При решении систем линейных уравнений используют метод Гаусса, который заключается в приведении заданной системы к треугольному виду (прямой ход). Затем из полученной треугольной системы переменные находят с помощью последовательных подстановок (обратный ход).
При выполнении прямого хода используют следующие преобразования:
умножение или деление коэффициентов свободных на одно и то же число;
сложение и вычитание уравнений;
перестановку уравнений системы;
исключение из системы уравнений, в которых все коэффициенты при неизвестных и свободные члены равны нулю.
x – y + 3 z = 3
З
апишем расширенную матрицу:
Чтобы в первом столбце получить a 2= a 3= 0, умножим первую строку соответственно на –3 и –2 и сложим результаты с первой строкой.
Первую и вторую строки запишем без изменения, а затем вторую строку умножим на 5, третью – на 4, полученные значения сложим и запишем результаты в качестве третьей строки:
1 –1 3 3
Запишем новую эквивалентную систему, которой соответствует расширенная матрица:
x – y + 3 z = 3
Выполняя обратный ход, найдём переменные:
4 y – 10 0 = 8; 4 y = 8; y = 2;
x – 2 + 3 0 = 3; x = 3 + 2 = 5.
Итак, получаем ответ: (5; 2; 0).
5 Решение систем линейных уравнений в матричной форме.
Для системы (1) рассмотрим матрицы
a1 b1 c1 d1 x1
Используя правило умножения матриц, систему (1) запишем в виде:
a1 b1 c1 x1 d1
Это равенство называется простейшим матричным уравнением.
Умножив обе части матричного уравнения на A -1 , получим: A -1 ( AX ) = A -1 D Так как ( A -1 A ) X = EX = X , ═ X = A -1 D .
Таким образом, чтобы решить матричное уравнение, нужно:
1). Найти обратную матрицу А -1 .
2). Найти произведение А -1 D .
3). Пользуясь определением равных матриц, записать ответ.
Пример. Решить матричное уравнение:
3 -1 0 5
Найдём обратную матрицу A -1 .
Вычислим определитель матрицы A :
3 -1 0
∆ = -2 1 1 = 12 – 2 + 3 – 8 = 5
Вычисляя алгебраические дополнения элементов матрицы, получим:
Запишем новую матрицу:
Запишем обратную матрицу:
0 1/5 1/5
1 4/5 –1/5 5 1 5 + 4/5 0 + (–1/5) 15 2
Х = 2 12/5 –3/5 0 = 2 5 + 12/5 0 + (–3/5) 15 1
0 1/5 1/5 15 0 5 + 1/5 0 + 1/5 15 3
Итак, можно записать:
х1 2
Задания для самостоятельной работы:
x + 2y + z = 8 2. x + 3y – 6z = 12
3x + 2y + z = 10 3x + 2y + 5z = –10
4x + 3y –2z = 4 2x + 5y – 3z = 6
Ответ: ( 1; 2; 3 ) Ответ: (0; 0; –2 )
3. 5 x – y – z = 0 4. 3x – y + 2z = 2
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать
Решение систем линейных уравнений различными методами
Методические рекомендации к практической работе № 2 по теме «Решение систем линейных уравнений различными методами»
Просмотр содержимого документа
«Решение систем линейных уравнений различными методами»
Методические рекомендации к практической работе № 2
«Решение систем линейных уравнений различными методами»
1. Система линейных уравнений
Обычно уравнения системы записывают в столбик одно под другим и объединяют фигурной скобкой
Система уравнений такого вида, где a, b, c – числа, а x, y — переменные, называется системой линейных уравнений.
При решении системы уравнений используют свойства, справедливые для решения уравнений.
2. Решение системы линейных уравнений способом подстановки
Рассмотрим пример 
1) Выразить в одном из уравнений переменную. Например, выразим y в первом уравнении, получим систему:
2) Подставляем во второе уравнение системы вместо y выражение 3х-7:
3) Решаем полученное второе уравнение:
4) Полученное решение подставляем в первое уравнение системы:
Система уравнений имеет единственное решение: пару чисел x = 1, y = — 4. Ответ: (1; -4), записывается в скобках, на первой позиции значение x, на второй — y.
3. Решение системы линейных уравнений способом сложения
Решим систему уравнений из предыдущего примера 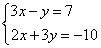методом сложения.
1) Преобразовать систему таким образом, чтобы коэффициенты при одной из переменных стали противоположными. Умножим первое уравнение системы на «3».
2) Складываем почленно уравнения системы. Второе уравнение системы (любое) переписываем без изменений.
3) Полученное решение подставляем в первое уравнение системы:
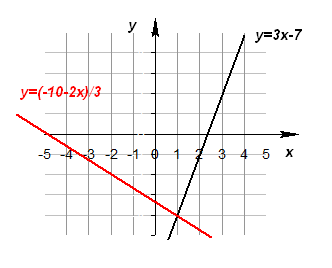
4. Решение системы линейных уравнений графическим способом
Графическое решение системы уравнений с двумя переменными сводится к отыскиванию координат общих точек графиков уравнений.
Графиком линейной функции является прямая. Две прямые на плоскости могут пересекаться в одной точке, быть параллельными или совпадать. Соответственно система уравнений может: а) иметь единственное решение; б) не иметь решений; в) иметь бесконечное множество решений.
2) Решением системы уравнений является точка (если уравнения являются линейными) пересечения графиков.
Графическое решение системы
Ответ: (1; -4).
Не решая системы линейных уравнений, можно определить число ее решений по коэффициентам при соответствующих переменных.
Пусть дана система (1)
1) Если , то система (1) имеет единственное решение.
2) Если ,, то система (1) решений не имеет.
В этом случае прямые, являющиеся графиками уравнений системы, параллельны и не совпадают.
.
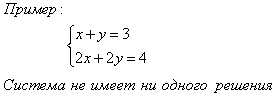
3) Если , то система (1) имеет бесконечное множество решений.
В этом случае прямые совпадают друг с другом.
.
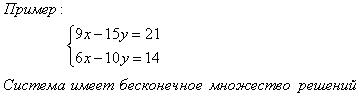
6.Решение систем линейных уравнений по формулам Крамера
Габриель Крамер (1704–1752) швейцарский математик.
Данный метод применим только в случае систем линейных уравнений, где число переменных совпадает с числом уравнений. Кроме того, необходимо ввести ограничения на коэффициенты системы. Необходимо, чтобы все уравнения были линейно независимы, то есть ни одно уравнение не являлось бы линейной комбинацией остальных. Для этого необходимо, чтобы определитель системы не равнялся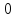 
.
Действительно, если какое-либо уравнение системы есть линейная комбинация остальных, то если к элементам какой-либо строки прибавить элементы другой, умноженные на какое-либо число, с помощью линейных преобразований можно получить нулевую строку. Определитель в этом случае будет равен нулю.
Система из двух уравнений с двумя неизвестными
решается с помощью формул Крамера:
, 
,
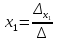
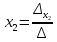
где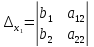 
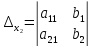
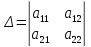
и 
, 
.
При решении системы возможны три случая:
1. Определитель системы . Тогда система имеет единственное решение, определяемое формулами Крамера.
2. Определитель системы . Если при этом хотя бы один из определителей и не равен нулю, то система не имеет решений.
3. Если , и , то одно из уравнений есть следствие другого, система сводится к одному уравнению с двумя неизвестными и имеет бесчисленное множество решений.
П р и м е р 1. Решить систему уравнений .
Решение. Вычислим определитель системы , и дополнительные определители ,
Система имеет единственное решение
П р и м е р 2. Решить систему уравнений .
Решение. Вычислим определитель системы , и дополнительные определители , . Коэффициенты уравнений системы пропорциональны, а свободные члены не подчинены той же пропорции. Система не имеет решений.
Ответ: нет решений.
П р и м е р 3. Решить систему уравнений
Решение. Вычислим определитель системы , и дополнительные определители .
Так как , то одно уравнение есть следствие другого (второе уравнение получено из первого умножением на ).
Система сводится к одному уравнению и имеет бесчисленное множество решений, каждое из которых вычисляется по формуле: , где числовые значения задаются произвольно и вычисляются соответствующие значения .
Ответ: – общее решение данной системы, а решения – частные.
Система из трех уравнений с тремя неизвестными
При решении системы из трех уравнений с тремя неизвестными возможны три случая:
1. Определитель системы . Система имеет единственное решение, определяемое формулами Крамера ,
2. Определитель системы равен нулю, . Если при этом хотя бы один из определителей , не равен нулю, то система несовместна, решений не имеет.
3. Если и , то система имеет бесчисленное множество решений.
П р и м е р 4. Решить систему уравнений
Решение. Вычислим определитель системы и дополнительные определители
По формулам Крамера имеем, что .
Метод Гаусса, называемый также методом последовательного исключения неизвестных, состоит в том, что при помощи элементарных преобразований систему линейных уравнений приводят к такому виду, чтобы её матрица из коэффициентов оказалась трапециевидной или близкой к трапециевидной.
Решите систему линейных уравнений методом Гаусса.
Решение. Выпишем расширенную матрицу системы и при помощи элементарных преобразований над ее строками приведем эту матрицу к ступенчатому виду (прямой ход) и далее выполним обратный ход метода Гаусса (сделаем нули выше главной диагонали). Вначале поменяем первую и вторую строку, чтобы элемент равнялся 1 (это мы делаем для упрощения вычислений):
Далее делаем нули под главной диагональю в первом столбце. Для этого от второй строки отнимаем две первых, от третьей — три первых:
Все элементы третьей строки делим на два
Далее делаем нули во втором столбце под главной диагональю, для удобства вычислений поменяем местами вторую и третью строки, чтобы диагональный элемент равнялся 1:
От третьей строки отнимаем вторую, умноженную на 3: Умножив третью строку на 0,5 , получаем:
Проведем теперь обратный ход метода Гаусса (метод Гассу-Жордана), то есть сделаем нули над главной диагональю. Начнем с элементов третьего столбца. Надо обнулить элемент , для этого от второй строки отнимем третью:
Далее обнуляем недиагональные элементы второго столбца, к первой строке прибавляем вторую:
Видео:Решение систем уравнений методом подстановкиСкачать
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ДЛЯ СТУДЕНТОВ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОГО ЗАНЯТИЯ «Решение систем линейных уравнений»
учебно-методический материал по математике на тему
Методические указания для выполнения практического занятия «Решение систем линейных уравнений», по дисциплине: Математика: алгебра и начала математического анализа, геометрия, созданы в помощь студентам, для успешной работы на занятие и подготовки к данному практическому занятию.
Видео:ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод ПодстановкиСкачать
Скачать:
| Вложение | Размер |
|---|---|
| m2.docx | 620.46 КБ |
Видео:Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать
Предварительный просмотр:
комитет образования и науки Волгоградской области
государственное бюджетное профессиональное образовательное учреждение
«Волжский политехнический техникум»
ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОГО ЗАНЯТИЯ
«Решение систем линейных уравнений»
Учебная дисциплина: Математика: алгебра и начала математического анализа, геометрия.
Специальности: 23.02.03, 13.02.11, 15.02.07
Автор: Курлович Елена Павловна, преподаватель первой квалификационной категории;
Методические указания для выполнения практического занятия «Решение систем линейных уравнений», по дисциплине: Математика: алгебра и начала математического анализа, геометрия, созданы в помощь студентам, для успешной работы на занятие и подготовки к данному практическому занятию.
Приступая к выполнению практического задания, студенты должны внимательно прочитать цели занятия, ознакомиться с общими сведения и примерами выполнения заданий, с критериями оценивания работы, ответить на контрольные вопросы для закрепления теоретического материала.
Наличие положительной оценки по практическому занятию необходимо для получения допуска к экзамену, поэтому в случае отсутствия на уроке по любой причине или получения неудовлетворительной оценки за практическое занятие, студенты должны найти время для его выполнения или пересдачи.
Если в процессе подготовки к практическому занятию или при решении задач у студентов возникают вопросы, разрешить которые самостоятельно не удается, необходимо обратиться к преподавателю для получения разъяснений или указаний в дни проведения дополнительных занятий.
Время проведения дополнительных занятий можно узнать у преподавателя или посмотреть на двери 122 кабинета.
Практическое занятие 2
Решение систем линейных уравнений.
способы решения систем 2-х линейных уравнений;
составлять из системы уравнений определитель 2 порядка, вычислять его, проводить исследование;
с помощью формул Крамера находить корни системы уравнений;
решать систему 2-х линейных уравнений способом сложения;
решать систему 2-х линейных уравнений способом подстановки;
решать систему 2-х линейных уравнений графическим способом;
Продолжительность занятия: 2 часа
Общие сведения и примеры выполнения заданий:
1. Решить систему уравнений способом сложения:
, 
Умножим почленно второе уравнение системы на , получим:
,
Теперь почленно сложим, левые и правые части уравнений системы:
Подставим в первое уравнение системы вместо число 30, найдем значение :
2. Решить систему уравнений способом подстановки:
Выразим из второго уравнения через
Подставим в первое уравнение вместо выражение :
Подставим вместо число 3 в уравнение :
3. Решить систему уравнений графическим способом:
Построим в координатной плоскости, графики уравнений системы.
Графиком первого уравнения является прямая , а графиком второго уравнения прямая . Точка — точка пересечения прямых, следовательно система имеет единственное решение
4. Пусть дана система двух линейных уравнений, с двумя неизвестными , коэффициенты не равны нулю
1. Если , то система имеет единственное решение.
2. Если , то система не имеет решений.
3. Если , то система имеет бесконечно много решений.
При каких значениях параметра система
а) имеет бесконечное множество решений;
б) имеет единственное решение?
а) Бесконечное множество решений, пункт 3: ;
б) Единственное решение, пункт 1:
При каких значениях параметра система
, не имеет решений.
Не имеет решений, пункт 2:
5. Решить систему уравнений методом Крамера:
| ;
, система имеет единственное решение.
Критерии оценивания работы:
1) Решить системы 2-х линейных- уравнений, любыми 2 способами: сложением, подстановкой, графически, методом Крамера .
2) Укажите какое-либо значение , при котором:
система имеет бесконечно много решений;
имеет единственное решение;
не имеет решений.
3) Решить систему 2-х уравнений по формулам Крамера.
1. Какие способы решения системы двух линейных уравнений с двумя переменными вам известны?
3. В чем заключается способ подстановки?
4. В чем состоит способ алгебраического сложения?
5. В чем заключается графический способ?
6. Что называется определителем второго порядка?
7. Формулы Крамера.
8. Когда система не имеет решений, имеет множество решений, единственное решение?
Задания для самостоятельной подготовки к практическому занятию:
Решить системы 2-х линейных- уравнений, любыми 2 способами: сложением, подстановкой, графически, методом Крамера:
a)
b)
a)
b)
Укажите какое-либо значение , при котором система
2 имеет единственное решение?
При каком значении система уравнений
9 имеет бесконечно много решений?
Решить систему 2-х уравнений по формулам Крамера:
1. Алгебра. 7 класс. Учебник. ФГОС. Авторы: Никольский С.М., Потапов М.К. и др. Издательство: Москва, Просвещение. Год: 2013
2. Сборник задач по математике: учеб. пособие для ссузов/Н.В.Богомолов.-5-е изд., М.: Дрофа, 2009
Видео:Решение системы уравнений методом ГауссаСкачать
По теме: методические разработки, презентации и конспекты
«Решение систем линейных уравнений» Урок обобщающего повторения
Урок разноуровневого обощающего повторения.
Презентация к уроку «Решение систем линейных уравнений» 7 класс
Презентация по теме : «Решение систем линейных уравнений» к уроку «Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций. На уроке решаются задачи с практичес.
Урок ао теме «Решение систем линейных уравнений» 7 класс
Урок по закреплению умений и навыков по решению систем линейных уравнений с двумя переменными. Содержит групповую работу, карту продуктивности, творческие задания.
Методическая разработка урока алгебры в 7 классе «Различные способы решения систем линейных уравнений» способы решения систем уравнений
Урок алгебры в 7 классе направлен на обобщение и систематизацию различных способов решения систем уравнений: метода сравнения, сложения, подстановки, графического метода, метода Крамера, выбора рацион.
Материалы к практическому занятию по математике для студентов специальности Экономика и бухгалтерский учет по теме «Графический метод решения систем линейных уравнений»
Данная разработка содержит конспект и презентацию к практическому занятию «Графический метод решения экономических задач» , завершающему изучение темы «Графический метод решения систем линейных уравне.
Методическая разработка для проведения занятия по теме «Решение систем линейных уравнений методом Крамера»
Тема урока: Способы решения линейных систем уравненийТип урока: урок первичного ознакомления с материаломДлительность: 1 час 20 мин.Технология — развитие критического мышления через чтение и письмоЦел.
Методическая разработка урока алгебры в 7 классе «Решение систем линейных уравнений с двумя переменными. Способ подстановки».
Цель урока: Сформировать умение решать системы двух линейных уравнений с двумя переменными способом подстановки.Задачи урока:образовательные:повторить понятие системы линейных уравнений с двумя переме.
🌟 Видео
Решение системы уравнений методом Крамера.Скачать
Решение системы уравнений методом Крамера 2x2Скачать
Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать
Решение системы линейных уравнений графическим методом. 7 класс.Скачать
Как ЛЕГКО РЕШАТЬ Систему Линейный Уравнений — Метод СложенияСкачать
Решение систем линейных уравнений с помощью матрицСкачать
Решение систем уравнений методом сложенияСкачать
Решение систем уравнений методом сложенияСкачать
10. Метод Крамера решения систем линейных уравнений.Скачать
Система уравнений. Метод алгебраического сложенияСкачать
12. Метод Гаусса решения систем линейных уравнений. Часть 1.Скачать
Метод Гаусса решения систем линейных уравненийСкачать
Матричный метод решения систем уравненийСкачать
СИСТЕМЫ УРАВНЕНИЙ В ЕГЭ ЧАСТЬ I #shorts #математика #егэ #огэ #профильныйегэСкачать
15. Однородная система линейных уравнений / фундаментальная система решенийСкачать
