Метод зейделя система из 3 уравнений

Метод Зейделя представляет собой некоторую модификацию метода простой итерации. Основная его идея заключается в том, что при вычислении (k+1)-го приближения неизвестной xi учитываются уже вычисленные ранее (k+1) – е приближения неизвестных x1, х2, .

В этом методе, как и в методе простой итерации, необходимо привести систему к виду (3), чтобы диагональные коэффициенты были максимальными по модулю, и проверить условия сходимости. Если условия сходимости не выполняются, то нужно произвести элементарные преобразования (см. п. 4). Пусть дана система из трех линейных уравнений. Приведем ее к виду (3). Выберем произвольно начальные приближения корней: х1(0), х2(0), х3(0), стараясь, чтобы они в какой-то мере соответствовали искомым неизвестным. За нулевое приближение можно принять столбец свободных членов, т. е. х(0) = b

(т. е. x1(0)=b1, x2(0)=b2, x3(0)=b3). Найдем Первое приближение х(1) по формулам:

Следует обратить внимание на особенность метода Зейделя, которая состоит в том, что полученное в первом уравнении значение х1(l) сразу же используется во втором уравнении, а значения х1(1), х2(1) – в третьем уравнении и т. д. То есть все найденные значения х1(1) подставляются в уравнения для нахождения хi+1(1) [6, 8].

Рабочие формулы для метода Зейделя для системы трех уравнений имеют следующий вид:

Запишем в общем виде для системы n-уравнений рабочие формулы:

Заметим, что теорема сходимости для метода простой итерации справедлива и для метода Зейделя.

Зададим определенную точность решения e, по достижении которой итерационный процесс завершается, т. е. решение продолжается до тех пор, пока не будет выполнено условие для всех уравнений: где i=1,2,3,…,n.

Пример №2. Методом Зейделя решить систему с точностью e = 10-3:

1. Приведем систему к виду:

2. В качестве начального вектора х(0) возьмем элементы столбца свободных членов, округлив их значения до двух знаков после запятой:

3. Проведем итерации методом Зейделя. При k = 1

.

При вычислении х2(1) используем уже полученное значение х1(1) =

.

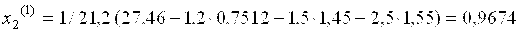
При вычислении х3(1) используем значения х1(1) и х2(1):

Наконец, используя значения х1(1), х2(1), х3(1), получаем:

Аналогичным образом ведем вычисления при k=2 и k=3. При k= 2:

Найдем модули разностей значений при k = 2:

Они меньше заданного числа e, поэтому в качестве решения возьмем: x1 = 0,80006, x2 = 1,00002, x3 = 1,19999, x4 = 1,40000.

Видео:Метод Зейделя Пример РешенияСкачать

Метод Гаусса-Зейделя: объяснение, приложения, примеры

Метод Гаусса-Зейделя: объяснение, приложения, примеры — Наука

Видео:Метод простой итерации Пример РешенияСкачать

Содержание:

В Метод Гаусса-Зейделя представляет собой итерационную процедуру для поиска приближенных решений системы линейных алгебраических уравнений с произвольно выбранной точностью. Метод применяется к квадратным матрицам с ненулевыми элементами на их диагоналях, и сходимость гарантируется, если матрица диагонально доминирует.

Он был создан Карлом Фридрихом Гауссом (1777-1855), который провел частную демонстрацию одному из своих учеников в 1823 году. Позднее он был официально опубликован Филиппом Людвигом фон Зайделем (1821-1896) в 1874 году, отсюда и название обоих математиков.

Для полного понимания метода необходимо знать, что матрица является доминирующей по диагонали, когда абсолютное значение диагонального элемента каждой строки больше или равно сумме абсолютных значений других элементов той же строки.

Математически это выражается так:

Видео:2.2 Итерационные методы решения СЛАУ (Якоби, Зейделя, релаксации)Скачать

Объяснение на простом случае

Чтобы проиллюстрировать, из чего состоит метод Гаусса-Зейделя, мы рассмотрим простой случай, в котором значения X и Y могут быть найдены в системе линейных уравнений 2 × 2, показанной ниже:

Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Шаги, которым нужно следовать

1- Во-первых, необходимо определить, безопасно ли схождение. Сразу видно, что это, по сути, диагонально доминирующая система, поскольку в первой строке первый коэффициент имеет более высокое абсолютное значение, чем другие в первой строке:

Точно так же второй коэффициент во второй строке также доминирует по диагонали:

2- Переменные X и Y решаются:

3- Ставится произвольное начальное значение, называемое «семя»: Xo = 1, I = 2.

4-Итерация начинается: для получения первого приближения X1, Y1 начальное число подставляется в первое уравнение этапа 2, а результат — во второе уравнение этапа 2:

X1 = (1-2 I) / 5 = (1-2 × 2) / 5 = -3/5

Y1 = X1 / 4 = (-3/5) / 4 = -3/20

5- Мы действуем аналогичным образом, чтобы получить второе приближение решения системы уравнений:

X2 = (1-2 Y1) / 5 = (1-2x (-3/20)) / 5 = 13/50

Y2 = X2 / 4 = (13/50) / 4 = 13/200

6- Третья итерация:

X3 = (1-2 Y2) / 5 = (1-2 (13/200)) / 5 = 87/500

Y3 = X3 / 4 = (87/500) / 4 = 87/2000

7- Четвертая итерация, как последняя итерация этого иллюстративного случая:

X4 = (1-2 Y3) / 5 = (1-2 (87/2000)) / 5 = 913/5000

Y4 = X4 / 4 = (913/5000) / 4 = 913/20000

Эти значения достаточно хорошо согласуются с решением, найденным другими методами разрешения. Читатель может быстро проверить это с помощью математической онлайн-программы.

Видео:Решение системы уравнений методом ГауссаСкачать

Анализ метода

Как видно, в методе Гаусса-Зейделя приблизительные значения, полученные для предыдущей переменной на том же шаге, необходимо подставить в следующую переменную. Это отличает его от других итерационных методов, таких как метод Якоби, в котором каждый шаг требует приближения предыдущего этапа.

Метод Гаусса-Зейделя не является параллельной процедурой, в отличие от метода Гаусса-Жордана. Это также причина того, что метод Гаусса-Зейделя имеет более быструю сходимость — за меньшее количество шагов — чем метод Жордана.

Что касается условия диагонального преобладания матрицы, то это не всегда выполняется. Однако в большинстве случаев для выполнения условия достаточно простой замены строк из исходной системы. Более того, метод почти всегда сходится, даже когда не выполняется условие диагонального доминирования.

Предыдущий результат, полученный с помощью четырех итераций метода Гаусса-Зейделя, можно записать в десятичной форме:

Точное решение предложенной системы уравнений:

Таким образом, всего 4 итерации дают результат с точностью до одной тысячной (0,001).

На рисунке 1 показано, как последовательные итерации быстро сходятся к точному решению.

Видео:Математика без Ху!ни. Метод Гаусса.Скачать

Приложения

Метод Гаусса-Зейделя не ограничивается только системой линейных уравнений 2 × 2. Предыдущая процедура может быть обобщена для решения линейной системы п уравнения с п неизвестных, которые представлены в виде матрицы:

КИкс = б

куда К это матрица п х п, Пока Икс — компоненты вектора n вычисляемых переменных; Y б — вектор, содержащий значения независимых слагаемых.

Чтобы обобщить последовательность итераций, примененных в иллюстративном случае к системе n x n, из которой должна быть вычислена переменная Си, будет применяться следующая формула:

В этом уравнении:

– k — индекс для значения, полученного на итерации k.

-k + 1 указывает новое значение в следующем.

Окончательное количество итераций определяется, когда значение, полученное на итерации к + 1 он отличается от полученного непосредственно перед этим на величину ε, которая и является желаемой точностью.

Видео:9 Метод Зейделя Ручной счет Решение системы линейных уравнений СЛАУСкачать

Примеры метода Гаусса-Зейделя

Видео:Метод_Зейделя_ExcelСкачать

— Пример 1

Напишите общий алгоритм вычисления вектора приближенных решений Икс линейной системы уравнений nxn, заданной матрицей коэффициентов К, вектор независимых слагаемых б, количество итераций (iтер) и начальное или «начальное» значение вектора Икс.

Видео:Решение системы трёх линейных уравнений методом Зейделя на VBAСкачать

Решение

Алгоритм состоит из двух циклов «До», один для количества итераций, а другой для количества переменных. Это было бы так:

X [i]: = (1 / A [i, i]) * (b [i] — ∑_{j = 1} п (A [i, j] * X [j]) + A [i, i] * X [i])

Видео:Олегу Тинькову запрещён вход на Мехмат МГУСкачать

— Пример 2

Проверить работу предыдущего алгоритма, применив его в математической программе. SMath Studio бесплатно, доступно для Windows и Android. Возьмем в качестве примера случай с матрицей 2 × 2, которая помогла нам проиллюстрировать метод Гаусса-Зейделя.

Видео:Решение системы уравнений методом Гаусса 4x4Скачать

Решение

Видео:Решение систем линейных алгебраических уравнений методом Зейделя (устар.)Скачать

— Пример 3

Примените алгоритм Гаусса-Зейделя для следующей системы уравнений 3 × 3, которая была предварительно упорядочена таким образом, что коэффициенты диагонали являются доминирующими (то есть имеют большее абсолютное значение, чем абсолютные значения коэффициентов тот же ряд):

9 Х1 + 2 Х2 — Х3 = -2

7 Х1 + 8 Х2 + 5 Х3 = 3

3 Х1 + 4 Х2 — 10 Х3 = 6

Используйте нулевой вектор в качестве начального числа и рассмотрите пять итераций. Прокомментируйте результат.

Видео:Матричный метод решения систем уравненийСкачать

Решение

Для той же системы с 10 итерациями вместо 5 получаются следующие результаты: X1 = -0,485; X2 = 1,0123; X3 = -0,3406

Это говорит нам о том, что пяти итераций достаточно для получения трех десятичных знаков точности и что метод быстро сходится к решению.

Видео:Метод Гаусса и метод Жордана-Гаусса ➜ 2 метода за 7 минутСкачать

— Пример 4

Используя приведенный выше алгоритм Гаусса-Зейделя, найдите решение системы уравнений 4 × 4, приведенной ниже:

10 х1 — х2 + 2 х3 + 0 х4 = 6

-1 х1 + 11 х2 — 1 х3 + 3 х4 = 25

2 x1 — 1 x2 + 10 x3 — 1 x4 = -11

0 х1 + 3 х2 — 1 х3 + 8 х4 = 15

Чтобы запустить метод, используйте это семя:

x1 = 0, x2 = 0, x3 = 0 и x4 = 0

Рассмотрим 10 итераций и оценим погрешность результата, сравнивая с итерацией номер 11.

Видео:Решение системы уравнений методом Крамера.Скачать

Решение

При сравнении со следующей итерацией (номер 11) результат идентичен. Наибольшие различия между двумя итерациями составляют порядка 2 × 10 -8 , что означает, что показанное решение имеет точность не менее семи десятичных знаков.

Видео:Решение системы уравнений методом Гаусса. Бесконечное множество решенийСкачать

Ссылки

1. Итерационные методы решения. Гаусс-Зайдель. Получено с: cimat.mx
2. Численные методы. Гаусс-Зайдель. Получено с: test.cua.uam.mx
3. Численный: метод Гаусса-Зейделя. Получено с: aprendeenlinea.udea.edu.co
4. Википедия. Метод Гаусса-Зейделя. Получено с: en. wikipedia.com
5. Википедия. Метод Гаусса-Зейделя. Получено с: es.wikipedia.com

Как мотивировать команду на работе: 8 советов

Видео:Решение матричных уравненийСкачать

Итерационные методы решения системы линейных алгебраических уравнений

В данной статье мы расскажем общие сведения об итерационных методах решения СЛАУ, познакомим с методом Зейделя и Якоби, а также приведем примеры решения систем линейных уравнений при помощи данных методов.

Видео:Метод Гаусса решения систем линейных уравненийСкачать

Общие сведения об итерационных методах или методе простой итерации

Метод итерации — это численный и приближенный метод решения СЛАУ.

Суть: нахождение по приближённому значению величины следующего приближения, которое является более точным. Метод позволяет получить значения корней системы с заданной точностью в виде предела последовательности некоторых векторов (итерационный процесс). Характер сходимости и сам факт сходимости метода зависит от выбора начального приближения корня x 0 .

Рассмотрим систему A x = b .

Чтобы применить итерационный метод, необходимо привести систему к эквивалентному виду x = B x + d . Затем выбираем начальное приближение к решению СЛАУ x ( 0 ) = ( x 1 0 , x 2 0 , . . . x m 0 ) и находим последовательность приближений к корню.

Для сходимости итерационного процесса является достаточным заданное условие В 1 . Окончание итерации зависит от того, какой итерационный метод применили.

Видео:Решение системы линейных уравнений методом ГауссаСкачать

Метод Якоби

Метод Якоби — один из наиболее простых методов приведения системы матрицы к виду, удобному для итерации: из 1-го уравнения матрицы выражаем неизвестное x 1 , из 2-го выражаем неизвестное x 2 и т.д.

Результатом служит матрица В , в которой на главной диагонали находятся нулевые элементы, а все остальные вычисляются по формуле:

b i j = — a i j / a i i , i , j = 1 , 2 . . . , n

Элементы (компоненты) вектора d вычисляются по следующей формуле:

d i = b i / a i i , i = 1 , 2 , . . . , n

Расчетная формула метода простой итерации:

x ( n + 1 ) = B x ( x ) + d

Матричная запись (координатная):

x i ( n + 1 ) = b i 1 x n 1 + b i 2 x ( n ) 2 + . . . + b

Критерий окончания в методе Якоби:

x ( n + 1 ) — x ( n ) ε 1 , где ε 1 = 1 — B B ε

В случае если B 1 / 2 , то можно применить более простой критерий окончания итераций:

x ( n + 1 ) — x ( n ) ε

Решить СЛАУ методом Якоби:

10 x 1 + x 2 — x 3 = 11 x 1 + 10 x 2 — x 3 = 10 — x 1 + x 2 + 10 x 3 = 10

Необходимо решить систему с показателем точности ε = 10 — 3 .

Приводим СЛАУ к удобному виду для итерации:

x 1 = — 0 , 1 x 2 + 0 , 1 x 3 + 1 , 1 x 2 = — 0 , 1 x 1 + 0 , 1 x 3 + 1 x 3 = 0 , 1 x 1 — 0 , 1 x 2 + 1

Выбираем начальное приближение, например: x ( 0 ) = 1 , 1 1 1 — вектор правой части.

В таком случае, первая итерация имеет следующий внешний вид:

x 1 ( 1 ) = — 0 , 1 × 1 + 0 , 1 × 1 + 1 , 1 = 1 , 1 x 2 ( 1 ) = — 0 , 1 × 1 , 1 + 0 , 1 + 1 = 0 , 99 x 3 ( 1 ) = 0 , 1 × 1 , 1 — 0 , 1 × 1 + 1 = 1 , 01

Аналогичным способом вычисляются приближения к решению:

x ( 2 ) = 1 , 102 0 , 991 1 , 011 , x ( 3 ) = 1 , 102 0 , 9909 1 , 0111 , x ( 4 ) = 1 , 10202 0 , 99091 1 , 01111

Находим норму матрицы В , для этого используем норму B ∞ .

Поскольку сумма модулей элементов в каждой строке равна 0,2, то B ∞ = 0 , 2 1 / 2 , поэтому можно вычислить критерий окончания итерации:

x ( n + 1 ) — x ( n ) ε

Далее вычисляем нормы разности векторов:

x ( 3 ) — x ( 2 ) ∞ = 0 , 002 , x ( 4 ) — x ( 3 ) ∞ = 0 , 00002 .

Поскольку x ( 4 ) — x ( 3 ) ∞ ε , то можно считать, что мы достигли заданной точности на 4-ой итерации.

x 1 = 1 , 102 ; x 2 = 0 , 991 ; x 3 = 1 ,01 1 .

Видео:Решение системы трех уравнений по формулам КрамераСкачать

Метод Зейделя

Метод Зейделя — метод является модификацией метода Якоби.

Суть: при вычислении очередного ( n + 1 ) — г о приближения к неизвестному x i при i > 1 используют уже найденные ( n + 1 ) — е приближения к неизвестным x 1 , x 2 , . . . , x i — 1 , а не n — о е приближение, как в методе Якоби.

x i ( n + 1 ) = b i 1 x 1 ( n + 1 ) + b i 2 x 2 ( n + 1 ) + . . . + b i , i — 1 x i — 2 ( n + 1 ) + b i , i + 1 x i + 1 ( n ) +

+ . . . + b i m x m ( n ) + d i

За условия сходимости и критерий окончания итераций можно принять такие же значения, как и в методе Якоби.

Решить СЛАУ методом Зейделя. Пусть матрица системы уравнений А — симметричная и положительно определенная. Следовательно, если выбрать начальное приближение, метод Зейделя сойдется. Дополнительных условий на малость нормы некоторой матрицы не накладывается.

Решим 3 системы уравнений:

2 x 1 + x 2 = 3 x 1 — 2 x 2 = 1 , x 1 + 2 x 2 = 3 2 x 1 — x 2 = 1 , 2 x 1 — 0 , 5 x 2 = 3 2 x 1 + 0 , 5 x 2 = 1

Приведем системы к удобному для итерации виду:

x 1 ( n + 1 ) = — 0 , 5 x 2 ( n ) + 1 , 5 x 2 ( n + 1 ) = 0 , 5 x 1 ( n + 1 ) + 0 , 5 , x 1 ( n + 1 ) = — 2 x 2 ( n ) + 3 x 2 ( n + 1 ) = 2 x 1 ( n + 1 ) — 1 , 2 x 1 — 0 , 5 x 2 = 3 2 x 1 + 0 , 5 x 2 = 1 .

Отличительная особенность, условие сходимости выполнено только для первой системы:

Вычисляем 3 первых приближения к каждому решению:

1-ая система: x ( 0 ) = 1 , 5 — 0 , 5 , x ( 1 ) = 1 , 75 0 , 375 , x ( 2 ) = 1 , 3125 0 , 1563 , x ( 3 ) = 1 , 4219 0 , 2109

Решение: x 1 = 1 , 4 , x 2 = 0 , 2 . Итерационный процесс сходится.

2-ая система: x ( 0 ) = 3 — 1 , x ( 1 ) = 5 9 , x ( 2 ) = — 15 — 31 , x ( 3 ) = 65 129

Итерационный процесс разошелся.

Решение: x 1 = 1 , x 2 = 2

3-я система: x ( 0 ) = 1 , 5 2 , x ( 1 ) = 2 — 6 , x ( 2 ) = 0 2 , x ( 3 ) = 0 2

Итерационный процесс зациклился.

Решение: x 1 = 1 , x 1 = 2

Метод простой итерации

Если А — симметричная и положительно определенная, то СЛАУ приводят к эквивалентному виду:

x = x — τ ( A x — b ) , τ — итерационный параметр.

Расчетная формула имеет следующий внешний вид:

x ( n + 1 ) = x ( n ) — τ ( A x n — b ) .

Здесь B = E — τ A и параметр τ > 0 выбирают таким образом, чтобы по возможности сделать максимальной величину B 2 .

Пусть λ m i n и λ m a x — максимальные и минимальные собственные значения матрицы А .

τ = 2 / ( λ m i n + λ m a x ) — оптимальный выбор параметра. В этом случае B 2 принимает минимальное значение, которое равняется ( λ m i n + λ m a x ) / ( λ m i n — λ m a x ) .