Метод зейделя онлайн система уравнений (4 видео)

1.2.3. Метод Зейделя (метод Гаусса-Зейделя, метод последовательных замещений)

Метод Зейделя представляет собой некоторую модификацию метода простой итерации. Основная его идея заключается в том, что при вычислении (k+1)-го приближения неизвестной xi учитываются уже вычисленные ранее (k+1) – е приближения неизвестных x1, х2, .

В этом методе, как и в методе простой итерации, необходимо привести систему к виду (3), чтобы диагональные коэффициенты были максимальными по модулю, и проверить условия сходимости. Если условия сходимости не выполняются, то нужно произвести элементарные преобразования (см. п. 4). Пусть дана система из трех линейных уравнений. Приведем ее к виду (3). Выберем произвольно начальные приближения корней: х1(0), х2(0), х3(0), стараясь, чтобы они в какой-то мере соответствовали искомым неизвестным. За нулевое приближение можно принять столбец свободных членов, т. е. х(0) = b

(т. е. x1(0)=b1, x2(0)=b2, x3(0)=b3). Найдем Первое приближение х(1) по формулам:

Следует обратить внимание на особенность метода Зейделя, которая состоит в том, что полученное в первом уравнении значение х1(l) сразу же используется во втором уравнении, а значения х1(1), х2(1) – в третьем уравнении и т. д. То есть все найденные значения х1(1) подставляются в уравнения для нахождения хi+1(1) [6, 8].

Рабочие формулы для метода Зейделя для системы трех уравнений имеют следующий вид:

Запишем в общем виде для системы n-уравнений рабочие формулы:

Заметим, что теорема сходимости для метода простой итерации справедлива и для метода Зейделя.

Зададим определенную точность решения e, по достижении которой итерационный процесс завершается, т. е. решение продолжается до тех пор, пока не будет выполнено условие для всех уравнений: где i=1,2,3,…,n.

Пример №2. Методом Зейделя решить систему с точностью e = 10-3:

1. Приведем систему к виду:

2. В качестве начального вектора х(0) возьмем элементы столбца свободных членов, округлив их значения до двух знаков после запятой:

3. Проведем итерации методом Зейделя. При k = 1

При вычислении х2(1) используем уже полученное значение х1(1) =

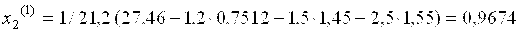
При вычислении х3(1) используем значения х1(1) и х2(1):

Наконец, используя значения х1(1), х2(1), х3(1), получаем:

Аналогичным образом ведем вычисления при k=2 и k=3. При k= 2:

Найдем модули разностей значений при k = 2:

Они меньше заданного числа e, поэтому в качестве решения возьмем: x1 = 0,80006, x2 = 1,00002, x3 = 1,19999, x4 = 1,40000.

Содержание

Итерационные методы решения системы линейных алгебраических уравнений
Общие сведения об итерационных методах или методе простой итерации
Метод Якоби
Метод Зейделя
Метод простой итерации
Gauss Seidel Calculator
Iteration Calculator
Formula:
🎬 Видео

Видео:2.2 Итерационные методы решения СЛАУ (Якоби, Зейделя, релаксации)Скачать

Итерационные методы решения системы линейных алгебраических уравнений

В данной статье мы расскажем общие сведения об итерационных методах решения СЛАУ, познакомим с методом Зейделя и Якоби, а также приведем примеры решения систем линейных уравнений при помощи данных методов.

Видео:Метод простой итерации Пример РешенияСкачать

Общие сведения об итерационных методах или методе простой итерации

Метод итерации — это численный и приближенный метод решения СЛАУ.

Суть: нахождение по приближённому значению величины следующего приближения, которое является более точным. Метод позволяет получить значения корней системы с заданной точностью в виде предела последовательности некоторых векторов (итерационный процесс). Характер сходимости и сам факт сходимости метода зависит от выбора начального приближения корня x 0 .

Рассмотрим систему A x = b .

Чтобы применить итерационный метод, необходимо привести систему к эквивалентному виду x = B x + d . Затем выбираем начальное приближение к решению СЛАУ x ( 0 ) = ( x 1 0 , x 2 0 , . . . x m 0 ) и находим последовательность приближений к корню.

Для сходимости итерационного процесса является достаточным заданное условие В 1 . Окончание итерации зависит от того, какой итерационный метод применили.

Видео:Метод Зейделя Пример РешенияСкачать

Метод Якоби

Метод Якоби — один из наиболее простых методов приведения системы матрицы к виду, удобному для итерации: из 1-го уравнения матрицы выражаем неизвестное x 1 , из 2-го выражаем неизвестное x 2 и т.д.

Результатом служит матрица В , в которой на главной диагонали находятся нулевые элементы, а все остальные вычисляются по формуле:

b i j = — a i j / a i i , i , j = 1 , 2 . . . , n

Элементы (компоненты) вектора d вычисляются по следующей формуле:

d i = b i / a i i , i = 1 , 2 , . . . , n

Расчетная формула метода простой итерации:

x ( n + 1 ) = B x ( x ) + d

Матричная запись (координатная):

x i ( n + 1 ) = b i 1 x n 1 + b i 2 x ( n ) 2 + . . . + b

Критерий окончания в методе Якоби:

x ( n + 1 ) — x ( n ) ε 1 , где ε 1 = 1 — B B ε

В случае если B 1 / 2 , то можно применить более простой критерий окончания итераций:

x ( n + 1 ) — x ( n ) ε

Решить СЛАУ методом Якоби:

10 x 1 + x 2 — x 3 = 11 x 1 + 10 x 2 — x 3 = 10 — x 1 + x 2 + 10 x 3 = 10

Необходимо решить систему с показателем точности ε = 10 — 3 .

Приводим СЛАУ к удобному виду для итерации:

x 1 = — 0 , 1 x 2 + 0 , 1 x 3 + 1 , 1 x 2 = — 0 , 1 x 1 + 0 , 1 x 3 + 1 x 3 = 0 , 1 x 1 — 0 , 1 x 2 + 1

Выбираем начальное приближение, например: x ( 0 ) = 1 , 1 1 1 — вектор правой части.

В таком случае, первая итерация имеет следующий внешний вид:

x 1 ( 1 ) = — 0 , 1 × 1 + 0 , 1 × 1 + 1 , 1 = 1 , 1 x 2 ( 1 ) = — 0 , 1 × 1 , 1 + 0 , 1 + 1 = 0 , 99 x 3 ( 1 ) = 0 , 1 × 1 , 1 — 0 , 1 × 1 + 1 = 1 , 01

Аналогичным способом вычисляются приближения к решению:

x ( 2 ) = 1 , 102 0 , 991 1 , 011 , x ( 3 ) = 1 , 102 0 , 9909 1 , 0111 , x ( 4 ) = 1 , 10202 0 , 99091 1 , 01111

Находим норму матрицы В , для этого используем норму B ∞ .

Поскольку сумма модулей элементов в каждой строке равна 0,2, то B ∞ = 0 , 2 1 / 2 , поэтому можно вычислить критерий окончания итерации:

x ( n + 1 ) — x ( n ) ε

Далее вычисляем нормы разности векторов:

x ( 3 ) — x ( 2 ) ∞ = 0 , 002 , x ( 4 ) — x ( 3 ) ∞ = 0 , 00002 .

Поскольку x ( 4 ) — x ( 3 ) ∞ ε , то можно считать, что мы достигли заданной точности на 4-ой итерации.

x 1 = 1 , 102 ; x 2 = 0 , 991 ; x 3 = 1 ,01 1 .

Видео:Математика без Ху!ни. Метод Гаусса.Скачать

Метод Зейделя

Метод Зейделя — метод является модификацией метода Якоби.

Суть: при вычислении очередного ( n + 1 ) — г о приближения к неизвестному x i при i > 1 используют уже найденные ( n + 1 ) — е приближения к неизвестным x 1 , x 2 , . . . , x i — 1 , а не n — о е приближение, как в методе Якоби.

x i ( n + 1 ) = b i 1 x 1 ( n + 1 ) + b i 2 x 2 ( n + 1 ) + . . . + b i , i — 1 x i — 2 ( n + 1 ) + b i , i + 1 x i + 1 ( n ) +

+ . . . + b i m x m ( n ) + d i

За условия сходимости и критерий окончания итераций можно принять такие же значения, как и в методе Якоби.

Решить СЛАУ методом Зейделя. Пусть матрица системы уравнений А — симметричная и положительно определенная. Следовательно, если выбрать начальное приближение, метод Зейделя сойдется. Дополнительных условий на малость нормы некоторой матрицы не накладывается.

Решим 3 системы уравнений:

2 x 1 + x 2 = 3 x 1 — 2 x 2 = 1 , x 1 + 2 x 2 = 3 2 x 1 — x 2 = 1 , 2 x 1 — 0 , 5 x 2 = 3 2 x 1 + 0 , 5 x 2 = 1

Приведем системы к удобному для итерации виду:

x 1 ( n + 1 ) = — 0 , 5 x 2 ( n ) + 1 , 5 x 2 ( n + 1 ) = 0 , 5 x 1 ( n + 1 ) + 0 , 5 , x 1 ( n + 1 ) = — 2 x 2 ( n ) + 3 x 2 ( n + 1 ) = 2 x 1 ( n + 1 ) — 1 , 2 x 1 — 0 , 5 x 2 = 3 2 x 1 + 0 , 5 x 2 = 1 .

Отличительная особенность, условие сходимости выполнено только для первой системы:

Вычисляем 3 первых приближения к каждому решению:

1-ая система: x ( 0 ) = 1 , 5 — 0 , 5 , x ( 1 ) = 1 , 75 0 , 375 , x ( 2 ) = 1 , 3125 0 , 1563 , x ( 3 ) = 1 , 4219 0 , 2109

Решение: x 1 = 1 , 4 , x 2 = 0 , 2 . Итерационный процесс сходится.

2-ая система: x ( 0 ) = 3 — 1 , x ( 1 ) = 5 9 , x ( 2 ) = — 15 — 31 , x ( 3 ) = 65 129

Итерационный процесс разошелся.

Решение: x 1 = 1 , x 2 = 2

3-я система: x ( 0 ) = 1 , 5 2 , x ( 1 ) = 2 — 6 , x ( 2 ) = 0 2 , x ( 3 ) = 0 2

Итерационный процесс зациклился.

Решение: x 1 = 1 , x 1 = 2

Видео:Метод простых итераций пример решения нелинейных уравненийСкачать

Метод простой итерации

Если А — симметричная и положительно определенная, то СЛАУ приводят к эквивалентному виду:

x = x — τ ( A x — b ) , τ — итерационный параметр.

Расчетная формула имеет следующий внешний вид:

x ( n + 1 ) = x ( n ) — τ ( A x n — b ) .

Здесь B = E — τ A и параметр τ > 0 выбирают таким образом, чтобы по возможности сделать максимальной величину B 2 .

Пусть λ m i n и λ m a x — максимальные и минимальные собственные значения матрицы А .

τ = 2 / ( λ m i n + λ m a x ) — оптимальный выбор параметра. В этом случае B 2 принимает минимальное значение, которое равняется ( λ m i n + λ m a x ) / ( λ m i n — λ m a x ) .

Видео:Решение систем линейных уравнений, урок 5/5. Итерационные методыСкачать

Gauss Seidel Calculator

An online Iteration calculator to solve a system of linear equations by Gauss Seidel Method, also known as the Liebmann method or the method of successive displacement.

Видео:9 Метод Зейделя Ручной счет Решение системы линейных уравнений СЛАУСкачать

Iteration Calculator

An online Iteration calculator to solve a system of linear equations by Gauss Seidel Method, also known as the Liebmann method or the method of successive displacement.

A step by step online Iteration calculator which helps you to understand how to solve a system of linear equations by Gauss Seidel Method.

Gauss-Seidel Method: It is an iterative technique for solving the n equations a square system of n linear equations with unknown x, where Ax =b only one at a time in sequence. This method is applicable to strictly diagonally dominant, or symmetric positive definite matrices A.

Formula:

In the below Gauss Seidel Calculator enter the number of equations (should be 2 to 10) to be examined and enter the values for the equations and click calculate to find the values of the variables in the equation. The properties of Gauss Seidel method are dependent on the matrix A. Liebmann method is an iteration method which is very useful in solving the linear equations quickly without much computations.