В этом разделе приведены примеры решенных задач по теме нахождения корней систем уравнений (как линейных, так и нелинейных) численными методами. Для первой группы (системы линейных алгебраических уравнений, СЛАУ) обычно используют методы Гаусса, простой итерации, Якоби, Зейделя, релаксации. Для второй группы — метод Ньютона, простой итерации, скорейшего спуска. Большая часть из них разобраны в подробных примерах ниже.
Видео:Метод простых итераций пример решения нелинейных уравненийСкачать

Примеры приближенных решений систем уравнений онлайн
Задача 1. Решить систему линейных уравнений $Ax=b$ методом Зейделя.
Итерационными методами решение задачи найти с точностью $varepsilon=10^$.
УКАЗАНИЕ. Для выполнения достаточного условия сходимости воспользоваться перестановкой строк в исходной системе уравнений.
Задача 2. 1) Решите систему линейных уравнений методом «Простой итерации» с точностью 0,001, предварительно оценив число достаточных для этого итераций:
2) Полученное решение используйте для вычисления невязки каждого уравнения.
3) Все полученные приближения решения системы привести в итоговом отчете.
4) Не забываем начинать отчет с формулировки задания.
Задача 3. 1) Методом Зейделя решите с точностью 0,001 систему линейных уравнений, приведя ее к виду с диагональным преобладанием, а затем к виду удобному для итераций.
2) Полученное решение используйте для вычисления невязки каждого уравнения.
3) Все полученные приближения решения системы привести в итоговом отчете.
4) Не забываем начинать отчет с формулировки задания.
Задача 4. Используя метод итераций, решите систему нелинейных уравнений с точностью до 0,001.
Задача 5. Используя метод Ньютона, решите систему нелинейных уравнений с точностью до 0,001.
Задача 6. Решить системы линейных уравнений с точностью до 0.001 методами простой итерации и Гаусса-Зейделя, предварительно проверив на сходимость.
Видео:Метод Зейделя Пример РешенияСкачать

Метод Гаусса–Зейделя
Одним из самых распространенных итерационных методов, отличающийся простотой и легкостью программирования, является метод Гаусса–Зейделя.
Проиллюстрируем сначала этот метод па примере решения системы

Предположим, что диагональные элементы а11, а22, а33отличны от нуля (в противном случае можно переставить уравнения). Выразим неизвестные х1, х2и х3 соответственно из первого, второго и третьего уравнений системы (2.27):



Зададим некоторые начальные (нулевые) приближения значений неизвестных: 


Используя это значение для x1 и приближение 
И наконец, используя вычисленные значения 
На этом заканчивается первая итерация решения системы (2.28) — (2.30). Теперь с помощью значений х1(1), х2(1)и х3(1)можно таким же способом провести вторую итерацию, в результате которой будут найдены вторые приближения к решению: х1 = х1 (2), х2 = х2(2)и х3 = х3(2)и т.д.
Приближение с номером kможно вычислить, зная приближение с номером k– 1, как
Итерационный процесс продолжается до тех пор, пока значения х1(k), х2(k)и х3(k)не станут близкими с заданной погрешностью к значениям х1(k-1), х2(k-1)и х3(k-1).
Пример. Решить с помощью метода Гаусса – Зейделя следующую систему уравнений:
Легко проверить, что решение данной системы следующее: х1 = х2 = х3 = 1.
Решение. Выразим неизвестные х1, х2и х3соответственно из первого, второго и третьего уравнений:
В качестве начального приближения (как это обычно делается) примем х1= 0, х2 = 0, х3 = 0. Найдем новые приближения неизвестных:
Аналогично вычислим следующие приближения:
Итерационный процесс можно продолжать до получения малой разности между значениями неизвестных в двух последовательных итерациях.
Рассмотрим теперь систему п линейных уравнений с п неизвестными. Запишем ее в виде
Здесь также будем предполагать, что все диагональные элементы отличны от нуля. Тогда в соответствии с методом Гаусса – Зейделя k-e приближение к решению можно представить в виде

Итерационный процесс продолжается до тех пор, пока все значения 

Для сходимости итерационного процесса (2.31) достаточно, чтобы модули диагональных коэффициентов для каждого уравнения системы были не меньше сумм модулей всех остальных коэффициентов (преобладание диагональных элементов):

При этом хотя бы для одного уравнения неравенство должно выполняться строго. Эти условия являются достаточными для сходимости метода, но они не являются необходимыми, т.е. для некоторых систем итерации сходятся и при нарушении условий (2.32).
Алгоритм решения системы п линейных уравнений методом Гаусса – Зейделя представлен на рис.2.6. В качестве исходных данных вводят п, коэффициенты и правые части уравнений системы, погрешность ε, максимально допустимое число итераций М, а также начальные приближения переменных xi(i=1,2,…,n).Отметим, что начальные приближения можно не вводить в компьютер, а полагать их равными некоторым значениям (например, нулю). Критерием завершения итераций выбрано условие (2.22), в котором через δобозначена максимальная абсолютная величина разности 

Для удобства чтения структурограммы объясним другие обозначения: k— порядковый номер итерации; i– номер уравнения, а также переменного, которое вычисляется в соответствующем цикле; j– номер члена вида 

Видео:2.2 Итерационные методы решения СЛАУ (Якоби, Зейделя, релаксации)Скачать

1.2.3. Метод Зейделя (метод Гаусса-Зейделя, метод последовательных замещений)
Метод Зейделя представляет собой некоторую модификацию метода простой итерации. Основная его идея заключается в том, что при вычислении (k+1)-го приближения неизвестной xi учитываются уже вычисленные ранее (k+1) – е приближения неизвестных x1, х2, .
В этом методе, как и в методе простой итерации, необходимо привести систему к виду (3), чтобы диагональные коэффициенты были максимальными по модулю, и проверить условия сходимости. Если условия сходимости не выполняются, то нужно произвести элементарные преобразования (см. п. 4). Пусть дана система из трех линейных уравнений. Приведем ее к виду (3). Выберем произвольно начальные приближения корней: х1(0), х2(0), х3(0), стараясь, чтобы они в какой-то мере соответствовали искомым неизвестным. За нулевое приближение можно принять столбец свободных членов, т. е. х(0) = b
(т. е. x1(0)=b1, x2(0)=b2, x3(0)=b3). Найдем Первое приближение х(1) по формулам:
Следует обратить внимание на особенность метода Зейделя, которая состоит в том, что полученное в первом уравнении значение х1(l) сразу же используется во втором уравнении, а значения х1(1), х2(1) – в третьем уравнении и т. д. То есть все найденные значения х1(1) подставляются в уравнения для нахождения хi+1(1) [6, 8].
Рабочие формулы для метода Зейделя для системы трех уравнений имеют следующий вид:
Запишем в общем виде для системы n-уравнений рабочие формулы:
Заметим, что теорема сходимости для метода простой итерации справедлива и для метода Зейделя.
Зададим определенную точность решения e, по достижении которой итерационный процесс завершается, т. е. решение продолжается до тех пор, пока не будет выполнено условие для всех уравнений: 
Пример №2. Методом Зейделя решить систему с точностью e = 10-3:
1. Приведем систему к виду:
2. В качестве начального вектора х(0) возьмем элементы столбца свободных членов, округлив их значения до двух знаков после запятой:
3. Проведем итерации методом Зейделя. При k = 1

При вычислении х2(1) используем уже полученное значение х1(1) =
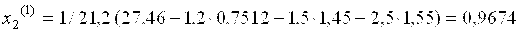
При вычислении х3(1) используем значения х1(1) и х2(1):
Наконец, используя значения х1(1), х2(1), х3(1), получаем:
Аналогичным образом ведем вычисления при k=2 и k=3. При k= 2:
Найдем модули разностей значений 
Они меньше заданного числа e, поэтому в качестве решения возьмем: x1 = 0,80006, x2 = 1,00002, x3 = 1,19999, x4 = 1,40000.
🎬 Видео
Метод_Зейделя_ExcelСкачать

9 Метод Зейделя Ручной счет Решение системы линейных уравнений СЛАУСкачать

Метод простой итерации Пример РешенияСкачать

Решение нелинейного уравнения методом простых итераций (программа)Скачать

4.2 Решение систем нелинейных уравнений. МетодыСкачать

Метод ЗейделяСкачать

6 Метод Зейделя Блок-схема Mathcad Calc Excel Решение системы линейных уравнений СЛАУСкачать

После этого видео, ТЫ РЕШИШЬ ЛЮБУЮ Систему Нелинейных УравненийСкачать

Математика без Ху!ни. Метод Гаусса.Скачать

МЗЭ 2021 Лекция 11 Метод Ньютона для решения систем нелинейных уравненийСкачать

Способы решения систем нелинейных уравнений. Практическая часть. 9 класс.Скачать

Способы решения систем нелинейных уравнений. Практическая часть. 9 класс.Скачать

1 3 Решение нелинейных уравнений методом простых итерацийСкачать

Решение систем линейных уравнений, урок 5/5. Итерационные методыСкачать

Метод итерацийСкачать

Методы численного анализа - Метод Ньютона, секущих для решения систем нелинейных уравненийСкачать

Метод Гуасса Зейделя, градиентный методСкачать






















