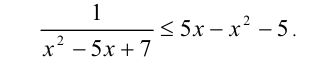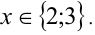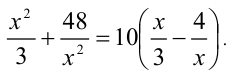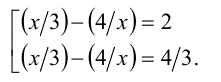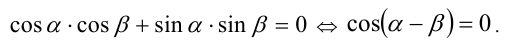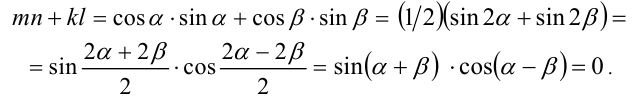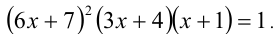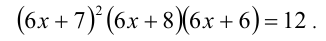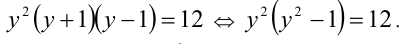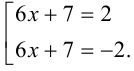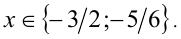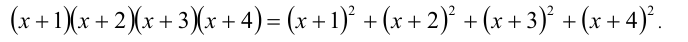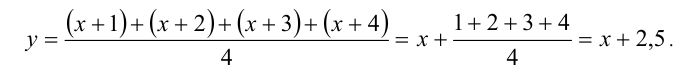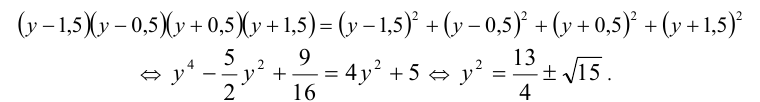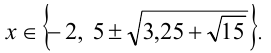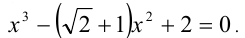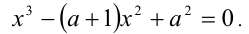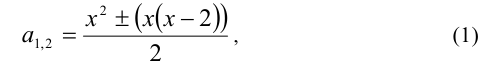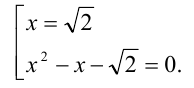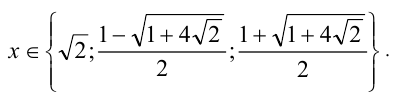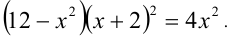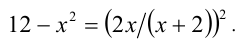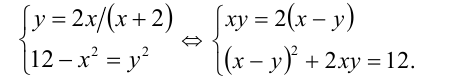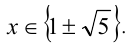Метод замены в решении уравнений

Метод замены переменной – это такой способ решения, при котором в уравнение (или неравенство) вводится новая переменная, в результате чего оно становится более простым.

Этот метод один из самых популярных при решении сложных заданий, в частности, в ЕГЭ и ОГЭ.

У нас довольно сложное уравнение. А если раскрыть скобки, оно станет еще сложнее. Что делать? Давайте попробуем заменить переменную.

Заменим выражение (x+frac) буквой (t).

Получилось обычное квадратное уравнение! Решив его, найдем чему равно (t), после чего, сделав обратную замену, вычислим (x).

Когда не стоит вводить новую переменную? Когда это не сделает уравнение проще. Например, если старая переменная остается, несмотря на замену:

Попробуем сделать замену здесь.

Заменим выражение (sin x) буквой (t).

Видим, что в этой замене нет никакого смысла – она не упростила уравнение, даже наоборот, усложнила его, потому что теперь у нас в уравнении две переменные.

Видео:Решение уравнения методом замены переменнойСкачать

Примеры использования метода замены переменной

Заметим, что (x^4=(x^2 )^2) (см. свойства степеней ). Тогда наше уравнение приобретает следующий вид.

Теперь используем метод замены.

Вводим новую переменную, заменяя (x^2) на (t).

Мы нашли чему равно (t), но найти-то надо иксы! Поэтому делаем обратную замену.

Ответ: (±1); (±) (frac) .

Весьма частая ошибка при использовании этого метода: забыть «вернуться к иксам», то есть не сделать обратную замену. Помните – нам нужно найти (x), а не (t)! Поэтому возврат к (x) — строго обязателен!

Пример. Решить неравенство: (log^2_3⁡x-log_3⁡x-2>0)

Приступим к решению.

Раскладываем левую часть неравенства на множители .

Теперь нужно вернуться к исходной переменной – иксу. Для этого перейдем к совокупности , имеющей такое же решение, и сделаем обратную замену.

Видео:Решение биквадратных уравнений. 8 класс.Скачать

Метод замены переменных при решении уравнений и неравенств

Метод замены переменных

Этот распространённый метод используется для разных целей: упрощение задачи и повышение её наглядности, придание уравнению (неравенству, системе и проч.) более симметричного вида, сведение одного уравнения к системе нескольких уравнений, рационализация иррациональностей (см. пункт 3.3) и т.д. Иными словами, введение новых переменных производится в тех случаях, когда есть возможность свести задачу к другой, для которой существует более эффективный способ решения.

Существуют виды уравнений, для которых разработаны специальные подстановки, позволяющие наиболее оптимально решать эти уравнения (например, симметрические и возвратные уравнения, однородные уравнения и многие другие). Рассмотрим дополнительно группу примеров, иллюстрирующих различные цели использования этого подхода.

Начнём с примера, в котором при помощи замены неизвестной рациональное неравенство сводится также к рациональному, но более простому алгебраическому неравенству.

Пример №350.

Решение:

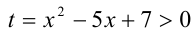
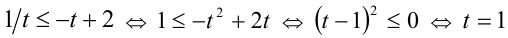
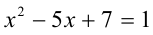
Положим . Тогда необходимо решить неравенство . Выполнив обратную подстановку, получим квадратное уравнение , решив которое, приходим к ответу. Ответ:

В следующем примере дробно-рациональное уравнение заменой сводится к целому алгебраическому уравнению.

Пример №351.

Решить уравнение

Решение:

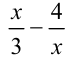
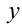
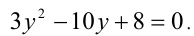
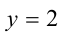
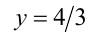
Обозначим разность через , тогда уравнение перепишется в виде Это уравнение имеет два корня и , что приводит к совокупности уравнений

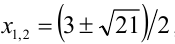
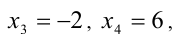
Первое уравнение даёт корни , а второе — которые и будут решениями исходного уравнения.

В некоторых случаях алгебраическую задачу (даже если в её условиях не содержится радикалов) с помощью специальных тригонометрических подстановок бывает целесообразно свести к тригонометрической задаче, и далее уже решать её методами тригонометрии.

Пример №352.

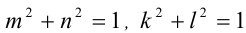
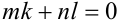
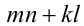
Известно, что и . Чему равно значение ?

Решение:

Воспользуемся тем, что если два действительных числа X, у удовлетворяют равенству

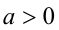
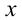
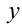
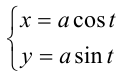
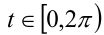
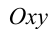
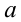
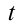
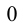
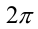
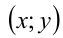
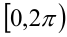
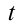
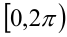
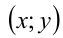
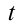
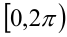
где — заданное число, то и можно представить в тригонометрическом виде , где . В самом деле, уравнение (1) задаёт на плоскости окружность радиуса с центром в начале координат. При изменении от до точка с координатами ровно один раз обходит окружность, и таким образом между точками окружности и полуинтервалом оказывается установлено взаимно однозначное соответствие. Это означает, что каждому значению из соответствует единственная пара чисел , удовлетворяющих равенству (1), и наоборот, каждой паре чисел, удовлетворяющих (1), соответствует единственное значение из .

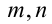
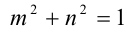
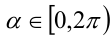
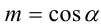
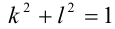
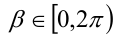
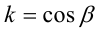
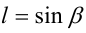
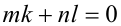
Итак, поскольку числа удовлетворяют равенству , то найдётся такое число , что , . Аналогично, поскольку числа удовлетворяют равенству , то найдётся такое число, что , . При этом условие примет вид

Выполнив тригонометрическую подстановку в искомом выражении 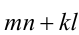, получим:

Введение новых переменных может быть вызвано необходимостью понизить степень уравнения, упростив при этом решение задачи.

Пример №353.

Решить уравнение

Решение:

Сведём данное уравнение 4-й степени к квадратному уравнению. Для этого вначале умножим обе части уравнения на 12 и приведём его к виду

Затем сделаем подстановку 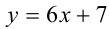, что приведёт к уравнению

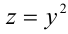
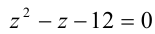
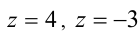
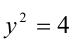
Сделав ещё одну подстановку , сведём окончательно данное биквадратное уравнение к квадратному уравнению , решив которое, находим корни . Тогда и

Ответ:

В следующем примере используется симметризирующая подстановка. Название говорит само за себя: уравнению придаётся более «симметричный» вид. Новая переменная является средним арифметическим входящих в уравнение выражений. При её применении уравнение 4-й степени общего вида приводится к более простому частному случаю, а именно, симметризация уравнения позволяет «убрать» из уравнения нечётные степени неизвестной, оставив только чётные и превратив его, таким образом, в биквадратное уравнение.

Пример №354.

Решение:

Выполним симметризирующую подстановку

Тогда уравнение примет вид

Ответ:

6.Близко к методу введения новых переменных стоит так называемый метод введения параметра. Не всегда введение параметра усложняет задачу. На примере, рассмотренном ниже, видно, как включение параметра в уравнение вместо числового коэффициента позволяет лучше «разглядеть» способ дальнейшего его решения — рассмотрение уравнения как квадратного относительно введённой величины.

Пример №355.

Решение:

Введём в уравнение параметр, положив :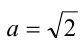

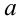
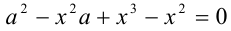
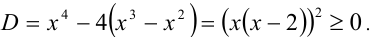
Рассмотрим теперь это уравнение как квадратное относительно . Приведём его к стандартному виду и вычислим дискриминант Найдём корни:

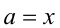
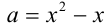
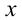
т.е. или . Параметр к этому моменту сыграл свою положительную роль, позволив свести решение кубического относительно уравнения к совокупности двух уравнений более низкой степени: квадратного и линейного.

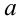
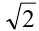
Заменяя числом , получим совокупность

Отсюда находим решения:

Замечание. В формуле корней квадратного уравнения более корректным было, вообще говоря, написать

Однако когда ищутся оба корня, то использование формул (1) и (2) приводит к одному результату. Именно поэтому часто в подобных ситуациях модуль опускают.

7.Отметим, что, вообще говоря, не всегда в задаче нужно полностью переходить к новым переменным. Иногда имеет смысл, вводя новую переменную, сохранить в задаче и первоначальную переменную, т.е. сделать частичную замену переменных. Так, сведением к системе уравнений, решаются некоторые уравнения. Рассмотрим в качестве пояснения пример.

Пример №356.

Решение:

Так как 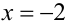не является корнем, то уравнение можно привести к равносильному виду

Положим 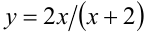, тогда уравнение сведётся к равносильной ему системе

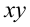
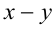
Решая эту систему относительно и , приходим к ответу:

Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:

Эти страницы возможно вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Видео:9 класс. Алгебра. Решение уравнений методом замены переменной.Скачать

Методы решения уравнений — обзор

В этой статье дан краткий обзор всех основных методов решения уравнений. Здесь также приведены ссылки на материалы с подробной информацией по каждому методу. Это дает возможность познакомиться со всеми методами решения уравнений, а в случае необходимости — изучить методы решения уравнений углубленно.

Видео:Зачётный способ решить дробно рациональное уравнение методом заменыСкачать

Метод введения новой переменной (замены переменной)

Метод введения новой переменной, он же метод замены переменной, позволяет решать уравнения f(g(x))=0 или f₁(g(x))=f₂(g(x)) , где f , f₁ и f₂ – некоторые функции, а x – неизвестная переменная, а также уравнения, которые могут быть приведены к указанному виду. Состоит метод во введении новой переменной t=g(x) . Введение переменной позволяет от исходного уравнения f(g(x))=0 или f₁(g(x))=f₂(g(x)) перейти к уравнению с новой переменной f(t)=0 или f₁(t)=f₂(t) соответственно. Дальше находятся корни полученного уравнения с новой переменной: t₁, t₂, …, t_n . После этого осуществляется возврат к старой переменной, для чего составляется совокупность уравнений g(x)=t₁, g(x)=t₂, …, g(x)=t_n . Решение этой совокупности дает интересующее нас решение исходного уравнения.

Например, метод введения новой переменной позволяет решить уравнение . Здесь стоит принять . Это позволяет перейти от исходного уравнения к квадратному уравнению t 2 −3·t+2=0 с новой переменной t , которое имеет два корня t₁=1 и t₂=2 . Обратная замена происходит путем составления совокупности двух уравнений и . Это рациональные уравнения. Решением первого является x=2 , а решением второго является x=1,5 . Так методом введения новой переменной получено решение исходного уравнения: 1,5 , 2 .

Подробное описание метода введения новой переменной, включающее обоснование метода, алгоритм решения уравнений этим методом и примеры решения характерных уравнений, дано в этой статье.

Видео:Алгебра 9 класс. Решение систем уравнений методом замены переменныхСкачать

Метод разложения на множители

Метод разложения на множители предназначен для решения уравнений f₁(x)·f₂(x)·…·f_n(x)=0 , где f₁(x), f₂(x),…, f_n(x) – некоторые выражения, x – переменная. То есть, методом разложения на множители решаются уравнения, в левой части которых находится произведение нескольких выражений, а в правой – нуль. Суть метода состоит в замене решения уравнения f₁(x)·f₂(x)·…·f_n(x)=0 решением совокупности уравнений f₁(x)=0, f₂(x)=0, …, f_n(x)=0 на области допустимых значений (ОДЗ) для исходного уравнения.

Приведем простой пример. Уравнение может быть решено методом разложения на множители. Переходим от исходного уравнения к совокупности двух уравнений и . Иррациональное уравнение имеет единственное решение x₁=1 . Логарифмическое уравнение тоже имеет единственное решение x₂=4 . Значит, совокупность уравнений имеет два решения x₁=1 , x₂=4 . Но области допустимых значений для исходного уравнения, которой является множество (3, +∞) , принадлежит лишь одно из решений x₁=1 , x₂=4 , а именно, x₂=4 . Оно и является единственным корнем уравнения .

Подробное описание этого метода и решения других характерных примеров смотрите в статье «метод разложения на множители».

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Метод решения уравнений «дробь равна нулю»

Из названия понятно, что этот метод используется при решении уравнений f(x)/g(x)=0 . Например, он позволяет решить уравнение . Метод состоит в переходе от решения уравнения f(x)/g(x)=0 к решению уравнения f(x)=0 на ОДЗ для исходного уравнения. Следовательно, чтобы решить уравнение , надо решить уравнение (x−1)·(x 2 −4)=0 на ОДЗ для исходного уравнения.

Обоснование метода и примеры с решениями смотрите здесь.

Видео:Математический анализ, 20 урок, Метод замены переменнойСкачать

Метод решения уравнений через преобразования

Метод базируется на преобразовании уравнений с целью выстраивания последовательностей равносильных уравнений и уравнений-следствий со сравнительно простыми последними уравнениями, по решениям которых находятся решения исходных уравнений.

Например, для решения уравнения 3·x 4 −48=0 последовательно проводятся два преобразования: переносится слагаемое −48 из левой части уравнения в правую с противоположным знаком, после чего проводится деление обеих частей уравнения на число 3 . В результате получается равносильное уравнение x 4 =16 , причем очень простое в плане решения. Оно имеет два корня x₁=−2 и x₂=2 . Они и составляют решение исходного уравнения.

Вот другой пример. Замена выражения в левой части уравнения тождественно равным выражением (x−1)·(x+2) дает уравнение-следствие (x−1)·(x+2)=0 , имеющее два корня x₁=1 и x₂=−2 . Проверка показывает, что только первый корень является корнем исходного уравнения, а второй корень – посторонний.

Какие преобразования используются при решении уравнений? Когда нужно делать проверку для отсеивания посторонних корней, а когда такую проверку делать необязательно? Ответы на эти и многие другие вопросы по теме есть в этом материале.

Видео:Алгебра Система уравнений Метод замены переменной № 6.22 9 классСкачать

Метод решения уравнений, сводящихся к числовым равенствам

Иногда в результате преобразования уравнений получаются числовые равенства. Например, уравнение сводится к верному числовому равенству 0=0 , а уравнение сводится к неверному числовому равенству 0=5 . Решением уравнений, сводящихся к верным числовым равенствам, является множество, совпадающее с ОДЗ для исходного уравнения. Так, решением уравнения является множество x≥0 . А уравнения, сводящиеся к неверным числовым равенствам, не имеют решений. То есть, уравнение не имеет решений.

Здесь есть один нюанс. Если среди преобразований, приводящих уравнение к верному числовому равенству, есть возведение обеих частей уравнения в одну и ту же четную степень, то нельзя утверждать, что решением уравнения является любое число из ОДЗ. Этот нюанс разобран в статье «решение уравнений, сводящихся к числовым равенствам».

Видео:Решение уравнений методом замены переменной.Скачать

Функционально-графический метод

Обзор методов решения уравнений продолжаем функционально-графическии методом. Этот метод предполагает использование функций, отвечающих частям решаемого уравнения, а точнее, их графиков и свойств. Можно выделить три основных направления функционально-графического метода:

• Графический метод
• Метод, базирующийся на возрастании-убывании функций
• Метод оценки

Давайте рассмотрим их.

Графический метод

Первое направление базируется на использовании графиков функций. Это так называемый графический метод решения уравнений. По этому методу, во-первых, выполняется построение в одной прямоугольной системе координат графиков функций, отвечающих частям уравнения. Во-вторых, по чертежу определяется количество точек пересечения графиков, сколько точек пересечения – столько и корней у решаемого уравнения. В-третьих, определяются абсциссы точек пересечения – это значения корней.

Например, графически можно решить уравнение . Из чертежа, приведенного ниже, видно, что графики имеют единственную точку пересечения с абсциссой 2 . Это единственный корень уравнения.

Метод, базирующийся на возрастании-убывании функций

Второе направление в своей основе имеет использование свойств возрастающих и убывающих функций. Соответствующий метод используется тогда, когда есть возможность подобрать корень уравнения и доказать возрастание функции, отвечающей одной из частей уравнения, и убывание функции, отвечающей другой части уравнения. В этом случае подобранный корень является единственным.
Приведем пример. Для уравнения 3 (1−x) 3 +1=2 x несложно подобрать корень, им является число 1 . Также несложно обосновать убывание функции, соответствующей левой части уравнения, и возрастание функции, отвечающей правой части уравнения. Это доказывает единственность подобранного корня.

За более полной информацией следуйте сюда

Метод оценки

Третье направление основано на использовании свойств ограниченности функций. Это так называемый метод оценки. Согласно этому методу, в первую очередь нужно оценить значения выражений, находящихся в левой и правой части уравнения. Если множества, соответствующие полученным оценкам, не пересекаются, то уравнение не имеет корней. Если множества имеют конечное число общих элементов t₁ , t₂ , …, t_n , то решение уравнения f(x)=g(x) заменяется решением совокупности систем , , …, . Если же множества, соответствующие оценкам имеют бесконечно много общих элементов, то надо либо уточнять оценки, либо искать другой метод решения.

Например, методом оценки можно решить уравнение . Значения левой части этого уравнения не превосходят нуля, а значения правой части не меньше нуля. Это позволяет перейти к системе , решение которой дает искомое решение уравнения.

Видео:решение уравнения с заменой переменнойСкачать

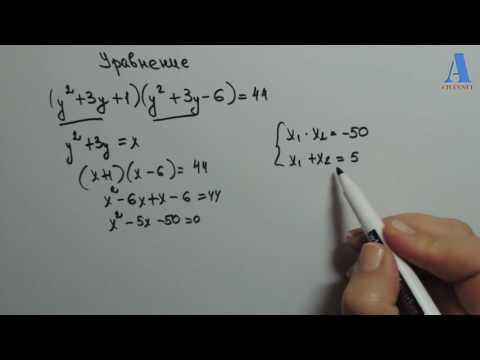
Метод освобождения от внешней функции

Метод освобождения от внешней функции используется для решения уравнений h(f(x))=h(g(x)) , где f , g и h – функции, причем функция y=h(t) принимает каждое свое значение по одному разу, в частности, строго возрастает или строго убывает, а x – независимая переменная. Этот метод состоит в переходе от уравнения h(f(x))=h(g(x)) к уравнению f(x)=g(x) на ОДЗ для исходного уравнения.

Например, методом освобождения от внешней функции можно решить уравнение . Здесь в качестве внешней функции выступает y=h(t) , где . Эта функция возрастающая как сумма двух возрастающих функций и , значит, каждое свое значение она принимает по одному разу. Это позволяет перейти от исходного уравнения к уравнению . Равносильные преобразования позволяют привести последнее уравнение к квадратному уравнению x 2 +x−2=0 , которое имеет два корня x₁=−2 и x₂=1 . Из этих корней только x₁=−2 принадлежит ОДЗ для исходного уравнения. Следовательно, x₁=−2 – единственный корень исходного уравнения.

Рекомендуем детально разобраться с этим методом решения уравнений, обратившись к материалу статьи «метод освобождения от внешней функции».

Видео:ОГЭ Задание 21 Решение уравнения методом заменыСкачать

Метод решения уравнений через ОДЗ

Через ОДЗ решаются уравнения, области допустимых значений которых являются либо пустыми множествами, либо состоят из конечного количества чисел. Когда ОДЗ есть пустое множество, уравнение не имеет решений. Когда ОДЗ состоит из конечного количества чисел, то следует по очереди проверить эти числа через подстановку. Те из них, которые удовлетворяют решаемому уравнению являются его корнями, остальные – не являются.

Например, уравнение не имеет решений, так как ОДЗ для него есть пустое множество. А для уравнения ОДЗ состоит из двух чисел −1 и 7 . Проверка подстановкой показывает, что −1 является корнем уравнения, а 7 – не является.

Более полная информация по этому методу решения уравнений содержится в этой статье.

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Метод возведения обеих частей уравнения в одну и ту же степень

Этот метод, в основном, используется для решения иррациональных уравнений. Он заключается в возведении обеих частей уравнения в одну и ту же степень с целью избавления от корней. Например, возведение обеих частей уравнения в квадрат дает уравнение без корня 1−5·x=(x−3) 2 . Возведение в нечетную степень дает равносильное уравнение. Возведение в четную степень в общем случае дает уравнение-следствие, поэтому, при этом необходимо позаботиться об отсеивании посторонних корней. Причем отсеивание следует проводить способом, не связанным с ОДЗ, обычно, через проверку подстановкой, так как возведение частей уравнения в четную степень может приводить к появлению посторонних корней в рамках ОДЗ.

Аналогично разбираемый метод может использоваться и для решения уравнений, в которых фигурируют степени с рациональными и иррациональными показателями. Решения соответствующих примеров смотрите здесь.

Видео:Решение системы неравенств с двумя переменными. 9 класс.Скачать

Метод решения уравнений по определению логарифма

По определению логарифма, как правило, решают уравнения следующего вида log_h(x)f(x)=g(x) , например, log₂(x 2 +4·x+3)=3 , log₂(9−2 x )=3−x , log_x(3·x lgx +4)=2·lgx и т.п.

Согласно методу решения уравнений по определению логарифма, решение уравнения log_h(x)f(x)=g(x) заменяется решением уравнения f(x)=(h(x)) g(x) на ОДЗ переменной x для исходного уравнения. Например, от уравнения log_x(3·x lgx +4)=2·lgx можно перейти к уравнению 3·x lgx +4=x 2·lgx на ОДЗ для исходного уравнения.

Более полная информация содержится в основной статье.

Видео:Метод введения новой переменной при решении иррациональных уравненийСкачать

Метод потенцирования

Методом потенцирования решаются логарифмические уравнения, обе части которых являются логарифмами по одному и тому же основанию, например, lgx=lg(3·x+5) , и т.п. Метод заключается в замене решения уравнения log_h(x)f(x)=log_h(x)g(x) решением уравнения f(x)=g(x) на ОДЗ для исходного уравнения. По этому методу от уравнения lgx=lg(3·x+5) следует перейти к уравнению x=3·x+5 на ОДЗ для исходного уравнения, которая определяется двумя условиями: x>0 , 3·x+5>0 .

Обоснование метода и примеры с подробными решениями смотрите в этой статье.

Видео:9 класс, 11 урок, Методы решения систем уравненийСкачать

Метод логарифмирования

Метод подразумевает логарифмирование обеих частей уравнения по одному и тому же основанию. К нему следует прибегать тогда, когда логарифмирование позволяет избавиться от степеней с переменной в показателях. В частности, его можно использовать для решения показательных уравнений, обе части которых являются степенями с одинаковыми основаниями, например, 5 1−x =5 2·x+1 . Почленное логарифмирование этого уравнения дает очень простое уравнение 1−x=2·x+1 , решение которого дает решение исходного уравнения.

Также метод подходит для решения показательных уравнений, степени в которых имеют разные основания и отличающиеся показатели, например, . Более того, метод логарифмирования является чуть ли не основным методом решения показательно-степенных уравнений, вроде таких x lgx−1 =100 , .

Более детальная информация и примеры с решениями есть в этом материале.

📺 Видео

Решение систем уравнений методом подстановкиСкачать

ПОЛНЫЙ разбор ВАРИАНТА №4 из сборника Добротина! | Химия ЕГЭ УМСКУЛСкачать

ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать

3.1 Интегрирование методом замены переменной. Часть 1Скачать

Уравнение Метод заменыСкачать