Рассмотрим линейное неоднородное дифференциальное уравнение первого порядка:
(1) .
Существует три способа решения этого уравнения:
Рассмотрим решение линейного дифференциального уравнения первого порядка методом Лагранжа.
- Метод вариации постоянной (Лагранжа)
- Шаг 1 Решение однородного уравнения
- Шаг 2 Заменим постоянную C на функцию
- Пример решения линейного дифференциального уравнения первого порядка методом Лагранжа
- Линейные неоднородные дифференциальные уравнения первого порядка
- Метод вариации произвольной постоянной для решения ЛНДУ первого порядка
- Подведем итог
- Еще один метод решения ЛНДУ первого порядка
- Линейные дифференциальные уравнения первого порядка. Метод вариации произвольной постоянной. Метод подстановки.
- 💥 Видео
Видео:Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать

Метод вариации постоянной (Лагранжа)
В методе вариации постоянной мы решаем уравнение в два этапа. На первом этапе мы упрощаем исходное уравнение и решаем однородное уравнение. На втором этапе мы заменим постоянную интегрирования, полученную на первой стадии решения, на функцию. После чего ищем общее решение исходного уравнения.
Шаг 1 Решение однородного уравнения
Ищем решение однородного уравнения:
Это уравнение с разделяющимися переменными
Разделяем переменные — умножаем на dx , делим на y :
Интегрируем:
Интеграл по y — табличный:
Тогда
Потенцируем:
Заменим постоянную e C на C и уберем знак модуля, что сводится к умножению на постоянную ±1 , которую включим в C :
Шаг 2 Заменим постоянную C на функцию
Теперь заменим постоянную C на функцию от x :
C → u ( x )
То есть, будем искать решение исходного уравнения (1) в виде:
(2)
Находим производную.
По правилу дифференцирования сложной функции:
.
По правилу дифференцирования произведения:
.
Подставляем в исходное уравнение (1):
(1) ;
.
Два члена сокращаются:
;
.
Интегрируем:
.
Подставляем в (2):
.
В результате получаем общее решение линейного дифференциального уравнения первого порядка:
.
Видео:9. Метод вариации произвольной постоянной ( метод Лагранжа ). Линейные дифференциальные уравнения.Скачать

Пример решения линейного дифференциального уравнения первого порядка методом Лагранжа
Решаем однородное уравнение:
Разделяем переменные:
Умножим на :
Интегрируем:
Интегралы табличные:
Потенцируем:
Заменим постоянную e C на C и убираем знаки модуля:
Отсюда:
Заменим постоянную C на функцию от x :
C → u ( x )
Находим производную:
.
Подставляем в исходное уравнение:
;
;
Или:
;
.
Интегрируем:
;
Решение уравнения:
.
Общее решение уравнения:
.
Автор: Олег Одинцов . Опубликовано: 27-07-2012 Изменено: 01-03-2015
Видео:7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

Линейные неоднородные дифференциальные уравнения первого порядка
В данной теме поговорим о способах решения линейных неоднородных дифференциальных уравнений вида y ‘ = P ( x ) · y = Q ( x ) . Начнем с метода вариации произвольной постоянной и покажем способ применения этого метода для решения задачи Коши. Продолжим рассмотрением метода, который предполагает представление произвольной постоянной у как произведения двух функций u ( x ) и v ( x ) . В разделе мы приводим большое количество задач по теме с детальным разбором решения.
На тот случай, если применяемые при разборе темы термины и понятия окажутся незнакомыми для вас, мы рекомендуем заглядывать в раздел «Основные термины и определения теории дифференциальных уравнений».
Видео:Метод Бернулли. Метод Лагранжа (вариации произвольной постоянной). Линейное дифуравнение 1 порядкаСкачать

Метод вариации произвольной постоянной для решения ЛНДУ первого порядка
Для краткости будет обозначать линейное неоднородное дифференциальное уравнение аббревиатурой ЛНДУ, а линейное однородное дифференциальное уравнение (ЛОДУ).
ЛНДУ вида y ‘ = P ( x ) · y = Q ( x ) соответствует ЛОДУ вида y ‘ = P ( x ) · y = 0 , при Q ( x ) = 0 . Если посмотреть на дифференциальное уравнение y ‘ = P ( x ) · y = 0 , становится понятно, что мы имеем дело с уравнением с разделяющимися переменными. Мы можем его проинтегрировать: y ‘ = P ( x ) · y = 0 ⇔ d y y = — P ( x ) d x , y ≠ 0 ∫ d y y = — ∫ P ( x ) d x ⇔ ln y + C 1 = — ∫ P ( x ) d x ⇔ ln y = ln C — ∫ P ( x ) d x , ln C = — C 1 , C ≠ 0 ⇔ e ln y = e ln C — ∫ P ( x ) d x ⇔ y = C · e — ∫ P ( x ) d x
Мы можем утверждать, что значение переменной y = 0 тоже является решением, так как при этом значении переменной уравнение y ‘ = P ( x ) · y = 0 обращается в тождество. Этому случаю соответствует решение y = C · e — ∫ P ( x ) d x при значении C = 0 .
Получается, что y = C · e — ∫ P ( x ) d x — общее решение ЛОДУ, где С – произвольная постоянная.
y = C · e — ∫ P ( x ) d x — это решение ЛОДУ y ‘ = P ( x ) · y = 0 .
Для того, чтобы найти общее решение неоднородного уравнения y ‘ = P ( x ) · y = Q ( x ) , будем считать С не константой, а функцией аргумента х . Фактически, мы примем y = C ( x ) · e — ∫ P ( x ) d x общим решением ЛНДУ.
Подставим y = C ( x ) · e — ∫ P ( x ) d x в дифференциальное уравнение y ‘ = P ( x ) · y = Q ( x ) . Оно при этом обращается в тождество:
y ‘ = P ( x ) · y = Q ( x ) C x · e — ∫ P ( x ) d x + P ( x ) · C ( x ) · e — ∫ P ( x ) d x = Q ( x )
Теперь обратимся к правилу дифференцирования произведения. Получаем:
C ‘ ( x ) · e — ∫ P ( x ) d x + C ( x ) · e — ∫ P ( x ) d x + P ( x ) · C ( x ) · e — ∫ P ( x ) d x = Q ( x )
Производная сложной функции e — ∫ P ( x ) d x ‘ равна e — ∫ P ( x ) d x · — ∫ P ( x ) d x ‘ .
Теперь вспомним свойства неопределенного интеграла. Получаем:
e — ∫ P ( x ) d x · — ∫ P ( x ) d x ‘ = — e — ∫ P ( x ) d x · P ( x )
Теперь выполним переход:
C ‘ ( x ) · e — ∫ P ( x ) d x + C ( x ) · e — ∫ P ( x ) d x ‘ + P ( x ) · C ( x ) · e — ∫ P ( x ) d x = Q ( x ) C ‘ ( x ) · e — ∫ P ( x ) d x — P ( x ) · C ( x ) · e — ∫ P ( x ) d x + P ( x ) · C ( x ) · e — ∫ P ( x ) d x = Q ( x ) C ‘ ( x ) · e — ∫ P ( x ) d x = Q ( x )
Так мы пришли к простейшему дифференциальному уравнению первого порядка. В ходе решения этого уравнения мы определим функцию C ( x ) . Это позволит нам записать решение исходного ЛНДУ первого порядка следующим образом:
y = C ( x ) · e — ∫ P ( x ) d x
Видео:Дифференциальные уравнения, 4 урок, Линейные дифференциальные уравнения первого порядкаСкачать

Подведем итог
Метод вариации произвольной постоянной при решении ЛНДУ предполагает проведение трех этапов:
- нахождение общего решения соответствующего ЛОДУ y ‘ + P ( x ) · y = 0 в виде y = C · e — ∫ P ( x ) d x ;
- варьирование произвольной постоянной С , что заключается в замене ее функцией С ( x ) ;
- подстановка функции y = C ( x ) · e — ∫ P ( x ) d x в исходное дифференциальное уравнение, откуда мы можем вычислить C ( x ) и записать ответ.
Теперь применим этот алгоритм к решению задачи.
Найдите решение задачи Коши y ‘ — 2 x y 1 + x 2 = 1 + x 2 , y ( 1 ) = 3 .
Нам нужно отыскать частное решение ЛНДУ y ‘ — 2 x y 1 + x 2 = 1 + x 2 при начальном условии y ( 1 ) = 3 .
В нашем примере P ( x ) = — 2 x 1 + x 2 и Q ( x ) = x 2 + 1 . Начнем с того, что найдем общее решение ЛОДУ. После этого применим метод вариации произвольной постоянной и определим общее решение ЛНДУ. Это позволит нам найти искомое частное решение.
Общим решением соответствующего ЛОДУ y ‘ — 2 x y 1 + x 2 = 0 будет семейство функций y = C · ( x 2 + 1 ) , где С – произвольная постоянная.
Варьируем произвольную постоянную y = C ( x ) · ( x 2 + 1 ) и подставляем эту функцию в исходное уравнение:
y ‘ — 2 x y 1 + x 2 = 1 + x 2 C x · ( x 2 + 1 ‘ — 2 x · C ( x ) · ( x 2 + 1 ) 1 + x 2 = 1 + x 2 C ‘ ( x ) · ( x 2 + 1 ) + C ( x ) · 2 x — 2 x · C ( x ) = 1 + x 2 C ‘ ( x ) = 1 ,
откуда C ( x ) = ∫ d x = x + C 1 , где C 1 – произвольная постоянная.
Это значит, что y = C ( x ) · ( x 2 + 1 ) = ( x + C 1 ) · ( x 2 + 1 ) — общее решение неоднородного уравнения.
Теперь приступим к отысканию частного решения, которое будет удовлетворять начальному условию y ( 1 ) = 3 .
Так как y = ( x + C 1 ) · ( x 2 + 1 ) , то y ( 1 ) = ( 1 + C 1 ) · ( 1 2 + 1 ) = 2 · ( 1 + C 1 ) . Обратившись к начальному условию, получаем уравнение 2 · ( 1 + C 1 ) = 3 , откуда C 1 = 1 2 . Следовательно, искомое решение задачи Коши имеет вид y = x + 1 2 · ( x 2 + 1 )
Теперь рассмотрим еще один метод решения линейных неоднородных дифференциальных уравнений y ‘ + P ( x ) · y = Q ( x ) .
Видео:19. Метод вариации произвольных постоянных. Линейные неоднородные диф уравнения 2-го порядкаСкачать

Еще один метод решения ЛНДУ первого порядка
Мы можем представить неизвестную функцию как произведение y = u ⋅ v , где u и v – функции аргумента x .
Мы можем подставить эту функцию в ЛНДУ первого порядка. Имеем:
y ‘ + P ( x ) · y = Q ( x ) ( u · v ) ‘ + P ( x ) · u · v = Q ( x ) u ‘ · v + u · v ‘ + P ( x ) · u · v = Q ( x ) u ‘ · v + u · ( v ‘ + P ( x ) · v ) = Q ( x )
Если найти такое v , чтобы оно было ненулевым частным решением дифференциального уравнения v ‘ + P ( x ) · v = 0 , то u можно будет определить из уравнения с разделяющимися переменными u ‘ · v = Q ( x ) .
Рассмотрим этот алгоритм решения на предыдущем примере. Это позволит нам сосредоточиться на главном, не отвлекаясь на второстепенные детали.
Найдите общее решение линейного неоднородного дифференциального уравнения y ‘ — 2 x y 1 + x 2 = 1 + x 2 .
Пусть y = u ⋅ v , тогда
y ‘ — 2 x y x 2 + 1 = x 2 + 1 ⇔ ( u · v ) — 2 x · u · v x 2 + 1 = x 2 + 1 u ‘ · v + u · v ‘ — 2 x · u · v x 2 + 1 = x 2 + 1 u ‘ · v + u · v ‘ — 2 x · v x 2 + 1 = x 2 + 1
Находим такое v , отличное от нуля, чтобы выражение в скобках обращалось в ноль. Иными словами, находим частное решение дифференциального уравнения v ‘ — 2 x · v x 2 + 1 = 0 .
v ‘ — 2 x · v x 2 + 1 = 0 ⇔ d v d x = 2 x · v x 2 + 1 ⇒ d v v = 2 x d x x 2 + 1 ⇔ d v v = d ( x 2 + 1 ) x 2 + 1 ∫ d v v = ∫ d ( x 2 + 1 ) x 2 + 1 ln v + C 1 = ln ( x 2 + 1 ) + C 2
Возьмем частное решение v = x 2 + 1 , соответствующее C 2 – С 1 = 0 .
Для этого частного решения имеем
u ‘ · v + u · v ‘ — 2 x · v x 2 + 1 = x 2 + 1 ⇔ u ‘ · ( x 2 + 1 ) + u · 0 = x 2 + 1 ⇔ u ‘ = 1 ⇔ u = x + C
Следовательно, общее решение исходного линейного неоднородного дифференциального уравнения есть y = u · v = ( x + C ) · ( x 2 + 1 )
Ответы в обоих случаях совпадают. Это значит, что оба метода решения, которые мы привели в статье, равнозначны. Выбирать, какой из них применить для решения задачи, вам.
Видео:Линейное дифференциальное уравнение первого порядка (1-x^2)*y'-xy=1Скачать

Линейные дифференциальные уравнения первого порядка. Метод вариации произвольной постоянной. Метод подстановки.
Читайте также:
|
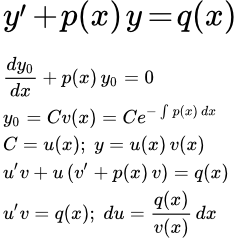
 , то (1)-наз. Однородное линейное ур-е, если же f(x)≠0, то (1)-неоднород.линейн. ур-е
, то (1)-наз. Однородное линейное ур-е, если же f(x)≠0, то (1)-неоднород.линейн. ур-е ln|y|=
ln|y|=  y=
y= 
 неизв. Ф-цию z(x)
неизв. Ф-цию z(x) z’-
z’-  =f(x)
=f(x)  y=(
y=( 
 u’
u’  =f(x);
=f(x);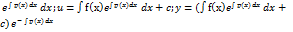



 — диф-ал ф-ции и обоз-ся dz. Dz=f’x(xy)
— диф-ал ф-ции и обоз-ся dz. Dz=f’x(xy)  +f’y(xy)
+f’y(xy)  . Предположим z=x. dz=dx=
. Предположим z=x. dz=dx=  . z=y: dz=dy=
. z=y: dz=dy=  => dz=f’x(xy)dx+d’y(xy)dy.
=> dz=f’x(xy)dx+d’y(xy)dy.
 [Пусть G-нек. Обл. Диаметром обл-ти наз-ся макс расстояние м/д граничными точками облG и обозн. d(G)] на каждой части Gi зафикс. Произвольн.образом точку (
[Пусть G-нек. Обл. Диаметром обл-ти наз-ся макс расстояние м/д граничными точками облG и обозн. d(G)] на каждой части Gi зафикс. Произвольн.образом точку (