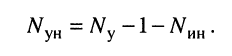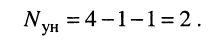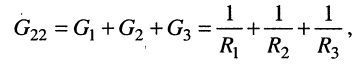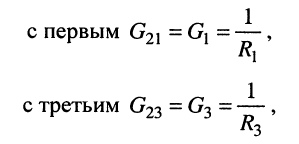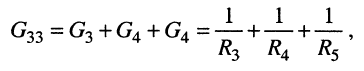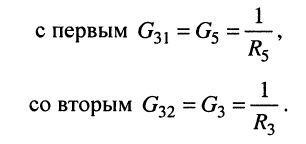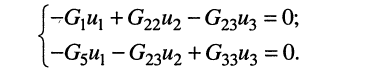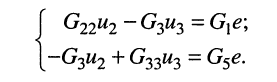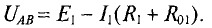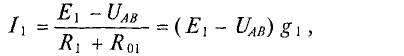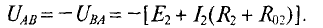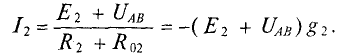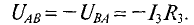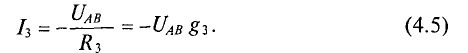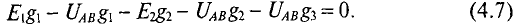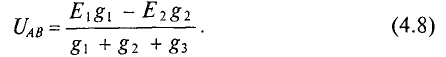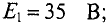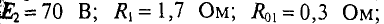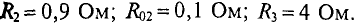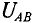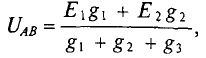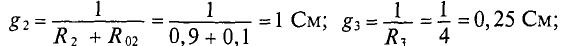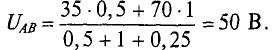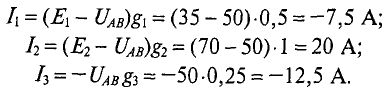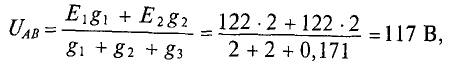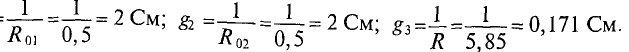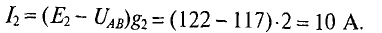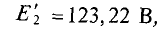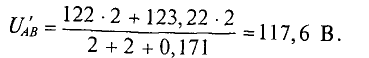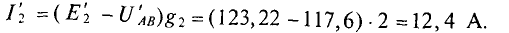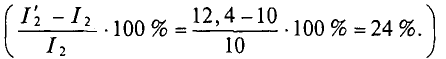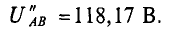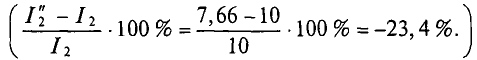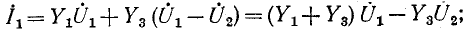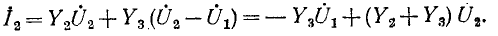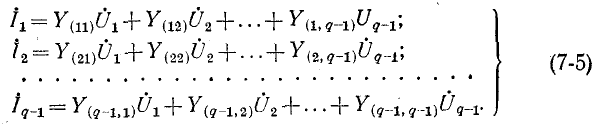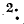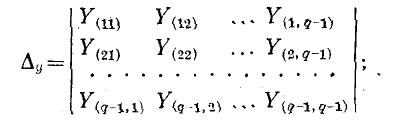При изучении основ электротехники приходится сталкиваться с необходимостью расчета тех или иных параметров различных схем. И самое простое, что приходится делать – это расчет токов ветвей в цепях постоянного тока.
Существует несколько наиболее применяемых методов расчетов для таких цепей: с помощью законов Кирхгофа, методом контурных токов, узловых потенциалов, методом эквивалентного генератора, эквивалентного источника тока, методом наложения. Для расчета более сложных цепей, например, в нелинейных схемах, могут применяться метод аппроксимации, графические методы и другие.
В данном разделе рассмотрим один из методов определения токов в цепи постоянного тока – метод узловых потенциалов.
- Метод узловых потенциалов примеры решения задач
- Метод узловых напряжений
- Составление узловых уравнений
- Особенности составления узловых уравнений
- Метод узлового напряжения
- Определение метода узловых напряжений
- Задачи по ТОЭ с решением и примерами
- Метод преобразования схем
- Пример задачи с решением 4.4
- Пример задачи с решением 4.6
- Метод узлового напряжения
- Пример задачи с решением 4.7
- Пример задачи с решением 4.8
- Параллельное соединение генераторов
- Метод узловых и контурных уравнений
- Пример задачи с решением 4.9
- Пример задачи с решением 4.10
- Метод контурных токов
- Пример задачи с решением 4.11
- Метод эквивалентного генератора
- Пример задачи с решением 4.12
- Пример задачи с решением 4.13
- 🔥 Видео
Метод узловых потенциалов примеры решения задач
Для того, чтобы лучше разобраться в этом вопросе, рассмотрим конкретный пример схемы, показанной на рис.1.




Для начала обозначают направления токов в ветвях. Направление можно выбирать любым. Если в результате вычислений какой-то из токов получится с отрицательным значением, значит, его направление в действительности будет направлено в противоположную сторону относительно ранее обозначенного. Если в ветви имеется источник, то для удобства лучше обозначить направление тока в этой ветви совпадающим с направлением источника в этой ветви, хотя и не обязательно. Далее один из узлов схемы заземляем. Заземленный узел будет называться опорным, или базисным. Такой метод заземления на общее токораспределение в схеме влияния не оказывает.
Каждый из этих узлов будет обладать своим значением потенциала относительно узла 4. Именно значения этих потенциалов для дальнейшего определения токов и находят. Соответственно, для удобства этим потенциалам присваивают номера в соответствии с номером узла, т.е. φ1, φ2, φ3. Далее составляется система уравнений для оставшихся узлов 1, 2, 3.
В общем виде система имеет вид:
Использованные в этой системе уравнений буквенно-цифровые обозначения
имеют следующий смысл:





Аналогично находятся и остальные проводимости:
J11 – узловой ток узла 1, в котором участвуют ветви, подходящие именно к этому узлу, и содержащие в своем составе ЭДС. При этом, если ЭДС ветви, входящий в узел, направлена к рассматриваемому узлу (в данном случае к узлу 1), то такой узловой ток записывается с плюсом, если от узла, то с минусом. В данном случае
В результате всех ранее приведенных вычисленных значений исходная система уравнений примет вид:
Решать данную систему можно всеми доступными методами, мы же для упрощения решим ее в пакете Mathcad:
В результате получены следующие значения потенциалов в узлах цепи:
Токи в ветвях находятся в соответствии с законом Ома. Поясним это простыми словами.
В ветви с сопротивлением и источником, учитывая ранее обозначенное направление тока в рассматриваемой ветви, необходимо из потенциала узла, находящегося у начала стрелки направления тока, вычесть потенциал узла, находящегося у конца стрелки направления тока, а затем прибавить значение ЭДС в этой ветви. Далее все это разделить на сопротивление, имеющееся в ветви. Если бы ток и ЭДС в рассматриваемой ветви не совпадали по направлению, тогда значение ЭДС вычиталось. В ветви без ЭДС действует то же самое правило, только ЭДС в числителе, разумеется, отсутствует. В нашем примере получим, что
Значение тока первой ветви, как видно из расчета, получилось отрицательным. Значит, в действительности, этот ток направлен в противоположную сторону относительно его обозначенного направления на рис.1.
Правильность расчетов можно проверить, например, составлением баланса мощностей либо, к примеру, моделированием, схемы. Выполним моделирование в программе Multisim.

Как видим, результаты моделирования совпадают с расчетными значениями. Незначительная разница в тысячных долях из-за округлений промежуточных вычислений.
Видео:Метод контурных токов - определение токов. ЭлектротехникаСкачать

Метод узловых напряжений
Содержание:
Метод узловых напряжений:
Метод узловых напряжений (узловых потенциалов) является наиболее общим. Он базируется на первом законе Кирхгофа (ЗТК) и законе Ома. В отличие от методов, рассмотренных в лекции 4, метод позволяет уменьшить число уравнений, описывающих схему, до величины, равной количеству рёбер (ветвей) дерева (2.1)
Идея метода состоит в следующем:
- Выбирается базисный узел — один из узлов цепи, относительно которого рассчитываются напряжения во всех узлах; базисный узел помечается цифрой 0.
- Потенциал базисного узла принимается равным нулю.
- Рассчитываются напряжения во всех узлах относительно базисного.
- По закону Ома находятся токи и напряжения в соответствующих ветвях.
Напряжения в узлах цепи, отсчитанные относительно базисного, называют узловыми напряжениями.
Определение:
Метод анализа колебаний в электрических цепях, в котором неизвестными, подлежащими определению, являются узловые напряжения, называется методом узловых напряжений.
В дальнейшем будем полагать, что цепь имеет
— задающий ток источника тока, который может быть подключён к
-му узлу; этот ток считается известным и характеризует воздействие на цепь;
— узловое напряжение
-го узла, отсчитанное относительно нулевого (базисного)узла;
— активная проводимость, связывающая £-ый и
-ый узлы;
— ток в ветви между
-ым и
-ым узлами, отсчитываемый от
-го узла в направлении
-го; токи, направления отсчётов которых ориентированы от узла, входят в уравнения со знаком «+ «;
— напряжение в ветви между
-ым и
-ым узлами.
Предварительно покажем, что при известных узловых напряжениях можно найти напряжения на всех элементах цепи, а потому и все токи. Действительно, напряжение на любой ветви определяется по второму закону Кирхгофа (ЗНК) как разность соответствующих узловых напряжений, а токи в элементах найдутся по закону Ома. Для контура, включающего элементы 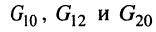
Аналогично можно записать
что и требовалось показать.
Видео:Метод узловых потенциалов - определение токов. ЭлектротехникаСкачать

Составление узловых уравнений
При составлении уравнений для, схемы рис. 5.1 будем полагать, что задающие токи 
Тогда согласно первому закону Кирхгофа для узлов 1 и 2 в предположении, что в общем случае они связаны со всеми другими узлами, получим:
Выразим токи в уравнениях через узловые напряжения, как показано в разд. 5.1:
Раскрыв скобки и приведя подобные члены, получаем узловые уравнения:
Полученный результат позволяет сделать следующие выводы:
- в левую часть каждого из уравнений входит N слагаемых, пропорциональных искомым узловым напряжениям
- коэффициент при узловом напряжении
-го узла, для которого составляется уравнение, представляет собой сумму проводимостей всех элементов, подключённых одним из своих зажимов к этому узлу; этот коэффициент входит в уравнение с положительным знаком;
- остальные слагаемые представляют собой произведение узлового напряжения на проводимость
элемента, связывающего

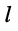
Аналогично записываются узловые уравнения для всех других узлов цепи, в результате чего образуется система узловых уравнений вида:
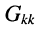


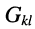

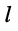

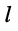
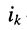



Систему узловых уравнений принято записывать в канонической форме, а именно:
- токи, как свободные члены, записываются в правых частях уравнений;
- неизвестные напряжения записываются в левых частях уравнений с последовательно возрастающими индексами;
- уравнения располагаются в соответствии с порядковыми номерами узлов. Такая запись применена в (5.2).
Система (5.2) является линейной неоднородной 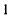
Метод узловых напряжений даёт существенное сокращение необходимого числа уравнений по сравнению с методом токов элементов. Выигрыш оказывается тем значительнее, чем больше независимых контуров имеет цепь.
Видео:Метод узловых потенциалов. Самое простое и понятное объяснение этого методаСкачать

Особенности составления узловых уравнений
Метод узловых напряжений можно применять и в тех случаях, когда в анализируемой цепи имеются источники напряжения. При этом:
- напряжение между любой парой узлов, к которым подключён источник напряжения, известно;
- в качестве базисного желательно выбирать узел, к которому одним из своих зажимов подключён источник напряжения — тогда узловое напряжение, отсчитываемое между базисным узлом и вторым зажимом источника, равно ЭДС источника или отличается от него знаком; кроме того, базисным может быть выбран узел, к которому подключено наибольшее число элементов, если этот выбор не противоречит первой рекомендаций;
- уменьшается число независимых узловых напряжений, а потому понижается и порядок системы, т. е. число входящих в систему независимых уравнений;
- если цепь содержит
источников напряжения, имеющих один общий зажим, то число узловых уравнений, которое можно составить для такой цепи, равно
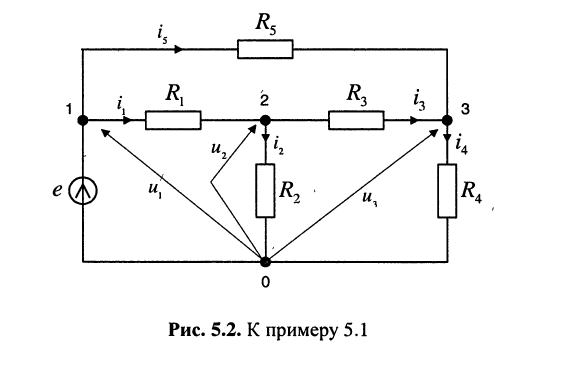
Пример 5.1.
Записать систему узловых уравнений для удлинителя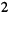
Решение. Удлинитель содержит четыре узла и один источник тока, поэтому согласно (5.3) достаточно составить всего два узловых уравнения
Положим узел 0 базисным, поскольку к нему одним из своих зажимов подключён источник напряжения. Узловое напряжение узла 1 известно и равно. ЭДС источника напряжения 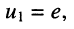
Собственная проводимость второго узла
взаимные проводимости второго узла
собственная проводимость третьего узла
взаимные проводимости третьего узла
Теперь получим систему узловых уравнений, записав узловые уравнения для второго и третьего узлов:
Поскольку 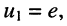
Эта система уравнений и является окончательным результатом решения задачи, поставленной в примере.
Если содержащиеся в цепи источники напряжения не имеют общего зажима, то задачу анализа следует решать или методом узловых напряжений в сочетании с принципом наложения или путём эквивалентных преобразований перейти к другой модели цепи.
При составлении узловых уравнений для цепей, содержащих многополюсники (например, транзисторы, операционные усилители
и т. д), следует прежде всего заменить эти многополюсники их схемами замещения.
Видео:Метод узловых и контурных уравненийСкачать

Метод узлового напряжения
Расчет сложных разветвленных электрических цепей с несколькими источниками и двумя узлам, можно осуществить методом узлового напряжения. Напряжение межи узлами и называется узловым. UAB R3 узловое напряжение цепи (рис. 4.9) Для различных ветвей (рис. 4.9) узловое напряжение UAB можно опредо лить следующим образом.
1. Поскольку для первой ветви источник работает в режиме генератор:
Величина тока определяется как
где 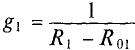
2.Для второй ветви источник работает в режиме потребителя следовательно
3.Для третьей ветви
(Потенциал точки В для третьей ветви больше, чем потенций точки А, так как ток направлен из точки с большим потенциалом в точку с меньшим потенциалом)
Величину тока 
По первому закону Кирхгофа для узловой точки А (или В):
Подставив в уравнение (4.6) значения токов из уравнений (4.3), .4) и (4.5) для рассматриваемой цепи, можно записать
Решив это уравнение относительно узлового напряжения UAB, можно определить его значение
Следовательно, величина узлового напряжения определяется отношением алгебраической суммы произведений ЭДС и проводимости ветвей с источниками к сумме проводимостей всех ветвей:
Для определения знака алгебраической суммы направление токов во всех ветвях выбирают одинаковым, т.е. от одного узла другому (рис. 4.9). Тогда ЭДС источника, работающего в режиме генератора, берется со знаком «плюс», а источника, работающего в режиме потребителя, со знаком «минус». Таким образом, для определения токов в сложной цепи с двумя узлами вычисляется сначала узловое напряжение по выражению 4.9), а затем значения токов по формулам (4.3), (4.4), (4.5). Узловое напряжение UAB может получиться положительным или отрицательным, как и ток в любой ветви.
Знак «минус» в вычисленном значении тока указывает, что реальное направление тока в данной ветви противоположно словно выбранному.
Пример 4.7
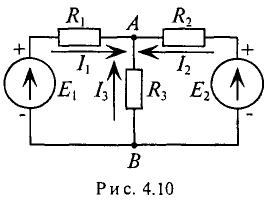
В ветвях схемы (рис. 4.10) требуется определить токи, если:
Решение
Узловое напряжение
где
тогда
Токи в ветвях будут соответственно равны
Как видно из полученных результатов, направление токов 
Пример 4.8
Два генератора (рис. 4.11), ЭДС и внутреннее сопротивление которых одинаковы: 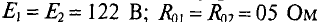
Как изменится ток второго генератора: 1) при увеличении его ЭДС (£2) на 1 %; » 2) при увеличении узлового напряжения (UAB) на 1 %.
Решение
Определяется узловое напряжение UAB цепи (рис. 4.11)
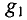
Тогда ток второго генератора
При увеличении Е2 на 1 %, его величина станет равной
При этом
Следовательно, увеличение ЭДС генератора Е2 на 1 % приводит увеличению тока этого генератора на 24 %.
2. При увеличении узлового напряжения на 1% его величины станет равной
При этом 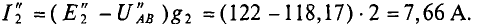
Знак «минус» означает уменьшение, а не увеличение тока 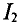
Видео:Метод узловых потенциаловСкачать

Определение метода узловых напряжений
Метод узловых напряжений заключается в том, что на основании первого закона Кирхгофа определяются потенциалы в узлах электрической цепи относительно некоторого базисного узла. Эти разности потенциалов называются узловыми напряжениями, причем положительное направление их указывается стрелкой от рассматриваемого узла к базисному.
Напряжение на какой-либо ветви равно, очевидно, разности узловых напряжений концов данной ветви; произведение же этого напряжения на комплексную проводимость данной ветви равно току в этой ветви. Таким образом, зная узловые напряжения в электрической цепи, можно найти токи в ветвях.
Если принять потенциал базисного узла равным нулю, то напряжения между остальными узлами и базисным узлом будут равны также потенциалам этих узлов. Поэтому данный метод называется также методом узловых потенциалов.
На рис. 7-7 в виде примера изображена электрическая схема с двумя источниками тока, имеющая три узла: 1, 2 и 3. Выберем в данной схеме в качестве базиса узел 3 и
обозначим узловые напряжения точек 1 и 2 через 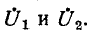
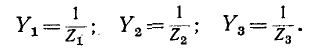
Для заданной электрической цепи с тремя узлами могут быть записаны два уравнения по первому закону Кирхгофа, а именно: для узла 1
Величина 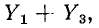
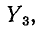
Если заданы токи источников тока и комплексные проводимости ветвей, то узловые напряжения находятся совместным решением уравнений.
В общем случае если электрическая схема содержит q узлов, то на основании первого закона Кирхгофа получается система из q — 1 уравнений (узел q принят за базисный):
Здесь ток источника тока, подходящий к узлу, берется со знаком плюс, а отходящий от узла — со знаком минус; 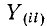
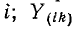
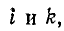
Решив систему уравнений (7-5) при помощи определителей 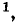
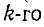
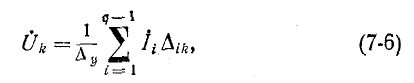
где 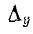
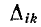
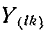
Первый индекс i алгебраического дополнения, обозначающий номер строки, вычеркиваемой в определителе системы, соответствует номеру узла, заданный ток источника тока которого умножается на данное алгебраическое дополнение. Второй индекс 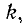
Уравнения (7-5), выражающие первый закон Кирхгофа, записаны в предположении, что в качестве источников электрической энергии служат источники тока. При наличии в электрической схеме источников э. д. с. последние должны быть заменены эквивалентными источниками тока.
Если в схеме имеются ветви, содержащие только э. д, с. (проводимости таких ветвей бесконечно велики), то эти ветви следует рассматривать как источники неизвестных токов, которые затем исключаются при сложении соответствующих уравнений. Дополнительными связями между неизвестными узловыми напряжениями будут являться известные напряжения между узлами, равные заданным э. д. с.
При наличии только одной ветви с э. д. с. и бесконечной проводимостью целесообразно принять за базисный узел один из узлов, к которому примыкает данная ветвь; тогда напряжение другого узла становится известным и число неизвестных сокращается на одно.
Метод узловых напряжений имеет преимущество перед методом контурных токов в том случае, когда число уравнений, записанных по первому закону Кирхгофа, меньше числа уравнений, записанных по второму закону Кирхгофа. Если заданная электрическая схема имеет q узлов и р ветвей, то в соответствии со сказанным выше, метод узловых напряжений представляет преимущество при q — 1
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Метод узловых потенциалов. Пример 1Скачать

Задачи по ТОЭ с решением и примерами
Содержание:
Метод преобразования схем
Метод преобразования электрических схем применяют для расчета сложных испей путем преобразований треугольника сопротивлений в эквивалентную звезду или звезды сопротивлений в эквивалентный треугольник.
Контур, состоящий из трех сопротивлений 

Электрическая цепь, состоящая из трех сопротивлений 

Расчет некоторых сложных цепей значительно упрощается, если соединение звездой в них заменить соединением треуголь-• ником или наоборот.
Преобразование схемы должно производиться так, чтобы при неизменном напряжении между точками 

Треугольник и звезда, удовлетворяющие этому условию, называются эквивалентными.
Для такого преобразования рекомендуется изображать схему цепи без заменяемого треугольника (или звезды), но с обозначенными вершинами 
При замене треугольника эквивалентной звездой сопротивления звезды определяются следующими выражениями:
Таким образом, каждое сопротивление эквивалентной звезды равно отношению произведения двух примыкающих к соответствующей узловой точке сопротивлений треугольника к сумме трех его сопротивлений.
При замене звезды эквивалентным треугольником каждое сопротивление треугольника определяется следующими выражениями:
Каждое сопротивление эквивалентного треугольника равно сумме трех слагаемых: двух примыкающих к соответствующим точкам сопротивлений звезды и отношению произведения этих сопротивлений к третьему сопротивлению звезды.
Пример задачи с решением 4.4
с Определить токи во всех ветвях цепи (рис. 4.7а) при следующих Исходных данных: 
Решение
Дчя расчета этой цепи заменим треугольник сопротивлений, Подключенных к точкам 
Определим величины сопротивлений эквивалентной звезды:

Пример задачи с решением 4.6
Определить токи во всех ветвях цепи, схема которой приведена на рис. 4.8а, если задано:
Решение
Количество ветвей и соответственно различных токов в цепи (рис. 4.8а) равно пяти. Произвольно выбирается направление этих токов.
Расчетных схем две, так как в цепи два источника с ЭДС 




Вычисление сопротивлений и токов производится методом свертывания.
Первые частичные токи в цепи (рис. 4.86), созданные источником 
Вычисляются частичные токи, созданные вторым источником. Для этого изображается исходная цепь, в которой источник :ЭДС 

Вторые частичные токи в цепи (рис. 4.8в) имеют следующие значения:
Искомые токи в рассматриваемой цепи (рис. 4.8а) определяют алгебраической суммой частичных токов (см. рис. 4.8):
Ток 
Метод узлового напряжения
Расчет сложных разветвленных электрических цепей с несколькими источниками и двумя узлам, можно осуществить 

Для различных ветвей (рис. 4.9) узловое напряжение 
1. Поскольку для первой ветви ис точник работает в режиме генератор;
Величина тока определяется как


2. Для второй ветви источник работает в режиме потребителя следовательно
3. Для третьей ветви
(Потенциал точки 
Величину тока 
По первому закону Кирхгофа для узловой точки А (или В):
Подставив в уравнение (4.6) значения токов из уравнений (4.3), (4.4) и (4.5) для рассматриваемой цепи, можно записать
Решив это уравнение относительно узлового напряжения 
Следовательно, величина узлового напряжения определяется от-ошением алгебраической суммы произведений ЭДС и проводимости етвей с источниками к сумме проводимостей всех ветвей.
Для определения знака алгебраической суммы направление токов во всех ветвях выбирают одинаковым, т. е. от одного узла другому (рис. 4.9). Тогда ЭДС источника, работающего в режиме генератора, берется со знаком «плюс», а источника, работающего в режиме потребителя, со знаком «минус».
Таким образом, для определения токов в сложной цепи с двумя злами вычисляется сначала узловое напряжение по выражению 4.9), а затем значения токов по формулам (4.3), (4.4), (4.5).
Узловое напряжение 
Знак «минус» в вычисленном значении тока указывает, что реальное направление тока в данной ветви противоположно ‘словно выбранному.
Пример задачи с решением 4.7
В ветвях схемы (рис. 4.10) требуется определить токи, если: 
Решение
I. Узловое напряжение
где

Токи в ветвях будут соответственно равны
Как видно из полученных результатов, направление токов 

Пример задачи с решением 4.8
Два генератора (рис. 4.11), ЭДС и внутреннее сопротивление которых одинаковы: 

Как изменится ток второго генератора:
1) при увеличении его ЭДС 
2) при увеличении узлового напряжения 
Решение
Определяется узловое напряжение 
Тогда ток второго генератора
I. При увеличении 
тогда
При этом 

2. При увеличении узлового напряжения на 1 % его величина станет равной
При этом
мм образом, ток второго генератора при увеличении узлово-.пряжения на 1 % уменьшится на 23,4 %.
Знак «минус» означает уменьшение, а не увеличение тока
Параллельное соединение генераторов
Как видно из решения примера 4.8, незначительное изменение ЭДС одного из параллельно работающих генераторов значительно изменяет ток этого генератора.
Причиной значительного изменения тока генератора может также незначительное изменение узлового напряжения 4.11), что связано с изменением сопротивлений участков или ЭДС источников.
Параллельное соединение генераторов нашло широкое примере в электрических сетях энергоснабжения потребителей осветительная и силовая нагрузка).
Значительные изменения токов генераторов, вызванные незна-пьными изменениями параметров схемы электропитания постелей от параллельно включенных генераторов, необходимо ывать при проектировании и эксплуатации электроустано-в частности тот факт, что в различное время суток работает ое количество параллельно включенных генераторов.
Увеличение ЭДС какого-либо из параллельно работающих генераторов приведет к тому, что ток этого генератора окажется в олько раз больше тока остальных генераторов. Этим обстоятельством пользуются, когда хотят «перевести нагрузку» с одного генератора на другой.
Генераторы окажутся также неодинаково загруженными при равых ЭДС, но при различных внутренних сопротивлениях. Более загруженными окажутся генераторы с меньшим внутренним сопротивлением.
И снижении ЭДС какого-либо из параллельно включенных раторов до величины узлового напряжения цепи 

Метод узловых и контурных уравнений
Метод узловых и контурных уравнений для расчета сложных электрических цепей подразумевает составление системы уравнений по законам Кирхгофа. При составлении системы уравнения должно учитываться следующее.
1. Число уравнений равно числу токов в цепи (число токов paвно числу ветвей в рассчитываемой цепи). Направление токов на ветвях выбирается произвольно.
2. По первому закону Кирхгофа составляется 
3. Остальные уравнения составляются по второму закону Кирхгофа.
В результате решения системы уравнений определяются иске мые величины для сложной электрической цепи (например, вс токи при заданных значениях ЭДС источников 
Пример задачи с решением 4.9
Составить необходимое и достаточное количество уравнени* по законам Кирхгофа для определения всех токов в цепи (рис. 4.12) методом узловых и контурный уравнений.
Решение
В рассматриваемой сложной цепи имеется 5 ветвей, сдедовательно, 5 различных токов, поэтому для расчета необходимо соста вить 5 уравнений, причем 2 уравнения — по первому закон: Кирхгофа (в цепи 


Обход по часовой стрелке.
Пример задачи с решением 4.10
Определить токи в примере 4.7 методом узловых и контурных уравнений (схема рис. 4.10) при тех же заданных условиях.
Решение
При выбранном в схеме рис. 4.10 направлении токов составим необходимое и достаточное количество уравнений по законам Кирхгофа:
1.
2. 
3. 
К уравнение (2) подставляются значения тока 
Иля сокращения тока 
Откуда
Из уравнения
И из уравнения (1):
Очевидно, что полученный результат совпадает с результатом полученным методом узлового напряжения.
Метод контурных токов
При расчете сложных цепей методом узловых и контурных уравнений (по законам Кирхгофа) необходимо решать систему из большого количества уравнений, что значительно затрудняет вычисления.
Так, для схемы рис. 4.13 необходимо составить и рассчитать систему из 7-ми уравнений.

Суть метода состоит в том, что в схеме выделяют т независимых контуров, в каждом из которых произвольно направлены (см. пунктирные стрелки) контурные токи 
Как видно из рис. 4.13, отдельные ветви схемы входят в два смежных контура. Действительный ток в такой ветви определяется алгебраической суммой контурных токов смежных контуров.
Для определения контурных токов составляют m уравнений по второму закону Кирхгофа. В каждое уравнение входит алгебраическая сумма ЭДС, включенных в данный контур (по одну сторону от знака равенства), и общее падение напряжения в данном контуре, созданное контурным током данного контура и контурными токами смежных контуров (по другую сторону знака равенства).
Для данной схемы (рис. 4.13) необходимо составить 4 уравнено знаком «плюс» записываются ЭДС и падения напряжению разные стороны знака равенства), действующие в направлении контурного тока, со знаком «минус» — направленные против контурного тока.
схема уравнений для схемы (рис. 4.13):
Решением системы уравнений вычисляются значения контурных токов, которые и определяют действительные токи в каждой схемы (рис. 4.13).
Пример задачи с решением 4.11
Определить токи во всех участках сложной цепи (рис. 4.14), если:
Решение
бходимо составить 3 уравнения по второму закону Кирхгофа для определения контурных токов 
Подставляются числовые значения величин
Из уравнения (2) определяется ток
Значение тока 
То же значение тока 
Из полученного уравнения (3) вычитается полученное уравнение (1). В результате получим
Откуда контурный ток
Из уравнения (3) определяется контурный ток
Из уравнения (2′) определяется ток
Вычисляются реальные токи в заданной цепи:
Проверяется правильность решения для 1-го контура (рис. 4.14).
Такую же проверку можно произвести и для других контуров (2-го и 3-го):
Проверка показала правильность решения.
Метод эквивалентного генератора
Метод эквивалентного генератора рационально применять в случае необходимости определения тока (напряжения, мощности и др.) только одной ветви сложной электрической цепи.
Для этой цели разбивают сложную электрическую цепь на две части — на сопротивление 



Активным этот двухполюсник называют потому, что в нем имеется источник ЭДС. Этот активный двухполюсник обладает определенной ЭДС 
Ток в резисторе с сопротивлением R определяют по закону Ома
Таким образом, определение тока I сводится к вычислению ЭДС эквивалентного гора 
чина ЭДС 


реннее сопротивление эквивалентного генератора Лж вы-тся относительно точек А и В после предварительной ,i всех источников сложной схемы эквивалентного генера-х внутренними сопротивлениями.
ггически для определения внутреннего сопротивления эк-нтного генератора измеряют амперметром ток между точ-4 и В работающего двухполюсника при коротком замыка-ак как сопротивление амперметра настолько мало, что им I пренебречь. Тогда
где 

Такой метод практического определения внутреннего сопротивления эквивалентного генератора 
Расчет параметров эквивалентного генератора, его ЭДС 

Пример задачи с решением 4.12
Определить ток в сопротивлении 

Для определения тока 




Знак «минус» обусловлен тем, что источники в схеме включень встречно и потенциал в точке А больше потенциала в точке В, так как 
Следовательно,
Внутреннее сопротивление эквивалентного генератора
Искомый ток
такой же ток получен в примере 4.6 на сопротивлении
Пример задачи с решением 4.13
На схеме рис. 4.17а сопротивления плеч моста равны
Сопротивление гальванометра 

Решение
Для определения тока в цепи гальванометра 




Для определения ЭДС эквивалентного генератора 
При замене источника ЭДС 



Тогда ток в ветви с гальванометром, который направлен из точки В в точку А, т. е. из точки с большим потенциалом в точку с меньшим потенциалом (рис. 4.17а), будет равен
Эти страницы вам могут пригодиться:
На странице -> решение задач по электротехнике собраны решения задач и заданий с решёнными примерами по всем темам теоретических основ электротехники (ТОЭ).
Услуги:
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
🔥 Видео
Урок 4. Расчет цепей постоянного тока. Законы КирхгофаСкачать

Метод узловых потенциалов, задача 1Скачать

Электротехника (ТОЭ). Лекция 5. Метод узловых потенциалов | Решение задачСкачать

ТОЭ - Метод двух узлов│Самое подробное решение задачиСкачать

Метод узловых потенциалов. Задача 2Скачать

Метод узлового напряженияСкачать

Метод узловых потенциалов. Решение задачи в программе mathcadСкачать

Метод узловых напряжений.Этапы 1—4 (видео 17) | Анализ цепей | ЭлетротехникаСкачать

Метод узловых потенциаловСкачать

РГУПС. (ТОЭ) 5 Постоянный ток. Метод узловых потенциалов. Метод двух узлов.Скачать

решение задачи составлением уравнений по правилам киргофа. Законы киргофа кратко на практикеСкачать

1 4 3 Метод узловых напряжениеСкачать

Лекция 117. Правила КирхгофаСкачать

Лекция 020-4. Метод узловых напряженийСкачать


















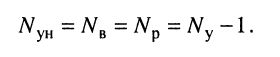
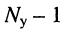
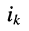 — задающий ток источника тока, который может быть подключён к
— задающий ток источника тока, который может быть подключён к 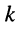 -му узлу; этот ток считается известным и характеризует воздействие на цепь;
-му узлу; этот ток считается известным и характеризует воздействие на цепь;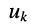 — узловое напряжение
— узловое напряжение 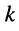 -го узла, отсчитанное относительно нулевого (базисного)узла;
-го узла, отсчитанное относительно нулевого (базисного)узла;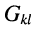 — активная проводимость, связывающая £-ый и
— активная проводимость, связывающая £-ый и 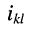 — ток в ветви между
— ток в ветви между 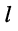 -ым узлами, отсчитываемый от
-ым узлами, отсчитываемый от 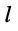 -го; токи, направления отсчётов которых ориентированы от узла, входят в уравнения со знаком «+ «;
-го; токи, направления отсчётов которых ориентированы от узла, входят в уравнения со знаком «+ «;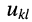 — напряжение в ветви между
— напряжение в ветви между  -ым узлами.
-ым узлами.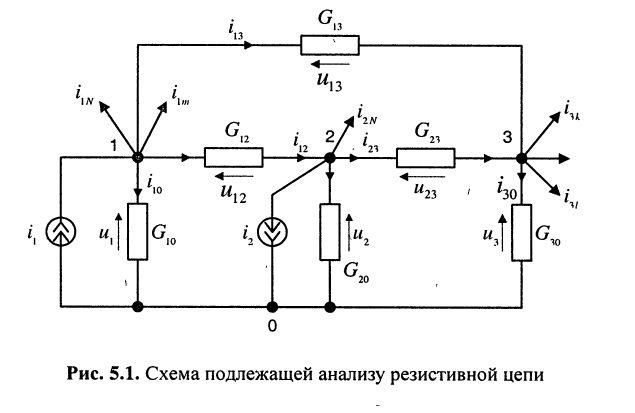
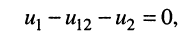
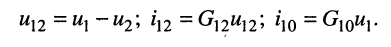
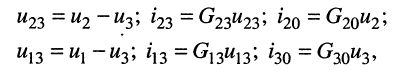
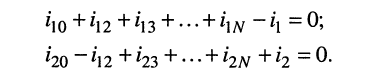
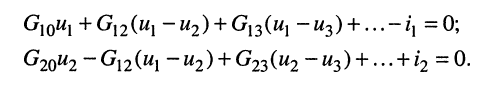
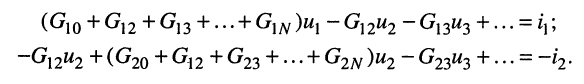
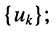
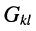 элемента, связывающего
элемента, связывающего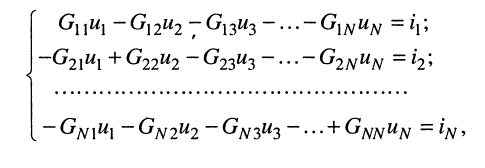
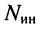 источников напряжения, имеющих один общий зажим, то число узловых уравнений, которое можно составить для такой цепи, равно
источников напряжения, имеющих один общий зажим, то число узловых уравнений, которое можно составить для такой цепи, равно