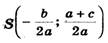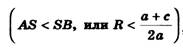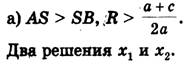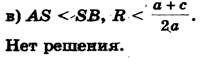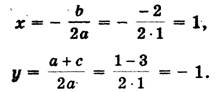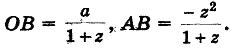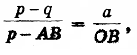8. СПОСОБ: Решение квадратных уравнений с помощью циркуля и линейки.
Графический способ решения квадратных уравнений с помощью параболы неудобен. Если строить параболу по точкам, то требуется много времени, и при этом степень точности получаемых результатов невелика.
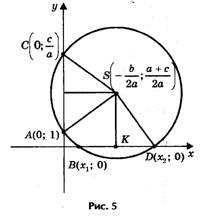
Предлагаю следующий способ нахождения корней квадратного уравнения ах 2 + bх + с = 0 с помощью циркуля и линейки (рис. 5).
Допустим, что искомая окружность пересекает ось
абсцисс в точках В(х1; 0 ) и D (х2; 0), где х1 и х2 — корни уравнения ах 2 + bх + с = 0, и проходит через точки
А(0; 1) и С(0; c/a) на оси ординат. Тогда по теореме о секущих имеем OB • OD = OA • OC, откуда OC = OB • OD/ OA= х1х2/ 1 = c/a.
Центр окружности находится в точке пересечения перпендикуляров SF и SK, восстановленных в серединах хорд AC и BD, поэтому
1) построим точки (центр окружности) и A(0; 1);
2) проведем окружность с радиусом SA;
3) абсциссы точек пересечения этой окружности с осью Ох являются корнями исходного квадратного уравнения.
При этом возможны три случая.
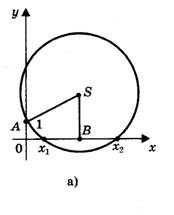
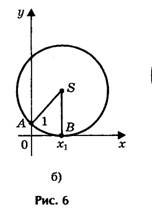
1) Радиус окружности больше ординаты центра (AS > SK, или R > a + c/2a), окружность пересекает ось Ох в двух точках (рис. 6,а) В(х1; 0) и D(х2; 0), где х1 и х2 — корни квадратного уравнения ах 2 + bх + с = 0.
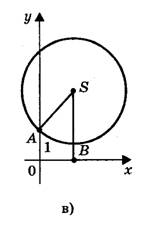
2) Радиус окружности равен ординате центра (AS = SB, или R = a + c/2a), окружность касается оси Ох (рис. 6,б) в точке В(х1; 0), где х1 — корень квадратного уравнения.
3) Радиус окружности меньше ординаты центра окружность не имеет общих точек с осью абсцисс (рис.6,в), в этом случае уравнение не имеет решения.
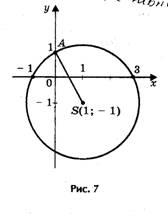
Решим уравнение х 2 — 2х — 3 = 0 (рис. 7).
Решение. Определим координаты точки центра окружности по формулам:
Проведем окружность радиуса SA, где А (0; 1).
9. СПОСОБ: Решение квадратных уравнений с помощью номограммы.
Это старый и незаслуженно забыты способ решения квадратных уравнений, помещенный на с.83 (см. Брадис В.М. Четырехзначные математические таблицы. — М., Просвещение, 1990).
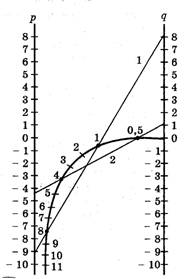
Таблица XXII. Номограмма для решения уравнения z 2 + pz + q = 0. Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициен там определить корни уравнения.
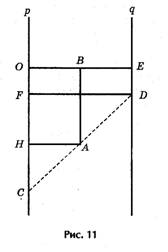
Криволинейная шкала номограммы построена по формулам (рис.11):
Полагая ОС = р, ED = q, ОЕ = а (все в см.), из подобия треугольников САН и CDF получим пропорцию
откуда после подстановок и упрощений вытекает уравнение
причем буква z означает метку любой точки криволинейной шкалы.
1) Для уравнения z 2 — 9z + 8 = 0 номограмма дает корни
2) Решим с помощью номограммы уравнение
Разделим коэффициенты этого уравнения на 2, получим уравнение
Номограмма дает корни z1 = 4 и z2 = 0,5.
3) Для уравнения
z 2 — 25z + 66 = 0
коэффициенты p и q выходят за пределы шкалы, выполним подстановку z = 5t, получим уравнение
t 2 — 5t + 2,64 = 0,
которое решаем посредством номограммы и получим t1 = 0,6 и t2 = 4,4, откуда z1 = 5t1 = 3,0 и z2 = 5t2 = 22,0.
- Решение квадратных уравнений с применением циркуля и линейки
- Описание презентации по отдельным слайдам:
- Охрана труда
- Охрана труда
- Библиотечно-библиографические и информационные знания в педагогическом процессе
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- Решение квадратных уравнений с помощью циркуля и линейки
- 🔥 Видео
Видео:Решение квадратных уравнений циркулем и линейкойСкачать
Решение квадратных уравнений с применением циркуля и линейки
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Описание презентации по отдельным слайдам:
Решение квадратных уравнений с применением циркуля и линейки
Выполнил.
Корни квадратного уравнения ах²+bx+c=0 (а≠0) можно рассматривать как абсциссы точек пересечения окружности с центром
Q, проходящей через точку А(0;1),
и оси Ох.
Решение уравнения сводится к построению на координатной плоскости окружности с центром Q и радиусом QA (для этого и понадобятся инструменты) и определению абсцисс точек пересечения окружности с осью Ох.
Возможны 3 случая:
1 случай
Если QA>то окружность пересекает ось Ох в двух точках М(х1 ; 0) и N( (х2 ; 0), уравнение имеет корни х1 , х2
х
у
Q
M
N
A
х1
х2
0
2 случай
Если QA= то окружность касается оси Ох в точке М(х1 ; 0), уравнение имеет корень х1 .
х
у
Q
M
A
х1
0
3 случай
Если QA -2,окружность
пересекает ох в двух
точках, уравнение имеет
2 корня.
Пример 3
Решите уравнение х²-4x+5=0.
Решение:
-в/2а=2, (а+с)/2а=3
Q(2;3), А(0;1)
QА
Курс повышения квалификации
Охрана труда
- Сейчас обучается 110 человек из 42 регионов
Курс профессиональной переподготовки
Охрана труда
- Сейчас обучается 230 человек из 54 регионов
Курс профессиональной переподготовки
Библиотечно-библиографические и информационные знания в педагогическом процессе
- Сейчас обучается 355 человек из 63 регионов
Ищем педагогов в команду «Инфоурок»
Видео:Решение квадратных уравнений с помощью циркуля и линейкиСкачать
Дистанционные курсы для педагогов
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 572 983 материала в базе
Другие материалы
- 27.12.2020
- 1343
- 4
- 27.12.2020
- 1546
- 44
- 27.12.2020
- 1581
- 5
- 27.12.2020
- 574
- 4
- 27.12.2020
- 486
- 0
- 27.12.2020
- 447
- 0
- 27.12.2020
- 356
- 1
- 27.12.2020
- 506
- 3
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 09.11.2020 302
- PPTX 74 кбайт
- 3 скачивания
- Оцените материал:
Настоящий материал опубликован пользователем Цыренов Эрдэм Николаевич. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 1 год и 1 месяц
- Подписчики: 0
- Всего просмотров: 31295
- Всего материалов: 236
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В России действуют более 3,5 тысячи студенческих отрядов
Время чтения: 2 минуты
Профессия педагога на третьем месте по популярности среди абитуриентов
Время чтения: 1 минута
Инфоурок стал резидентом Сколково
Время чтения: 2 минуты
В школах Хабаровского края введут уроки спортивной борьбы
Время чтения: 1 минута
Тринадцатилетняя школьница из Индии разработала приложение против буллинга
Время чтения: 1 минута
Количество бюджетных мест в вузах по IT-программам вырастет до 160 тыс.
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Видео:Решение квадратных уравнений. Метод разложения на множители. 8 класс.Скачать
Решение квадратных уравнений с помощью циркуля и линейки
Аннотация. Статья представляет собой один из способов уравнений с помощью циркуля и линейки. Благодаря такому способу решения уравнений, его можно применять в различных уравнениях в математике для нахождения корней уравнения.
Ключевые слова: квадратное уравнение, циркуль, линейка, метод координат.
Таким образом, данный способ решения квадратных уравнений является одним из наиболее простых, потому что занимает небольшое количество времени и не требует больших усилий. В данной статье объяснён принцип нахождения корней уравнения, правильного применения формулы для их вычисления.
Ссылки на источники
- Википедия. Определение квадратных уравнений [Электронный ресурс]- URL: https://ru.wikipedia.org/wiki/%CA%E2%E0%E4%F0%E0%F2%ED%EE%E5_%F3%F0%E0%E2%ED%E5%ED%E8%E5
- Решение уравнений с помощью циркуля и линейки [Электронный ресурс]- URL: http://5klass.net/algebra-9-klass/Reshenie-kvadratnykh-uravnenij-9-klass/018-Reshenie-uravnenij-s-pomoschju-tsirkulja-i-linejki.html
- Википедия. Решение уравнений с помощью циркуля и линейки [Электронный ресурс] — URL:
- https://ru.wikipedia.org/wiki/%CA%E2%E0%E4%F0%E0%F2%ED%EE%E5_%F3%F0%E0%E2%ED%E5%ED%E8%E5#.D0.A0.D0.B5.D1.88.D0.B5.D0.BD.D0.B8.D0.B5_.D0.BA.D0.B2.D0.B0.D0.B4.D1.80.D0.B0.D1.82.D0.BD.D1.8B.D1.85_.D1.83.D1.80.D0.B0.D0.B2.D0.BD.D0.B5.D0.BD.D0.B8.D0.B9_.D1.81_.D0.BF.D0.BE.D0.BC.D0.BE.D1.89.D1.8C.D1.8E_.D1.86.D0.B8.D1.80.D0.BA.D1.83.D0.BB.D1.8F_.D0.B8_.D0.BB.D0.B8.D0.BD.D0.B5.D0.B9.D0.BA.D0.B8
- Графические методы решения уравнений[Электронный ресурс] — URL: http://www.nado5.ru/e-book/graficheskii-sposob-resheniya-uravnenii
- Решение квадратных уравнений с помощью номограммы[Электронный ресурс] — URL: http://refdb.ru/look/2941907.html
1. Википедия. Определение квадратных уравнений [Электронный ресурс]- URL: https://ru.wikipedia.org/wiki/%CA%E2%E0%E4%F0%E0%F2%ED%EE%E5_%F3%F0%E0%E2%ED%E5%ED%E8%E5
2. Решение уравнений с помощью циркуля и линейки [Электронный ре-сурс]- URL: http://5klass.net/algebra-9-klass/Reshenie-kvadratnykh-uravnenij-9-klass/018-Reshenie-uravnenij-s-pomoschju-tsirkulja-i-linejki.html
3. Википедия. Решение уравнений с помощью циркуля и линейки [Элек-тронный ресурс] — URL:
🔥 Видео
Неполные квадратные уравнения. Алгебра, 8 классСкачать
Решение квадратных уравнений. Дискриминант. 8 класс.Скачать
Решение биквадратных уравнений. 8 класс.Скачать
Метод переброски в квадратных уравнениях. ЕГЭ и ОГЭ 2022 по математикеСкачать
Метод переброски при решении квадратных уравненийСкачать
Быстрый способ решения квадратного уравненияСкачать
Метод выделения полного квадрата. 8 класс.Скачать
Как брать корень квадратный с помощью циркуля и линейки?Скачать
Алгебра 8. Урок 9 - Квадратные уравнения. Полные и неполныеСкачать
Вы умеете решать квадратные уравнения?Скачать
СУММА КОЭФФИЦИЕНТОВ: Как решать Квадратные Уравнения по МАТЕМАТИКЕ 8 классСкачать
Ал-Хорезми и квадратные уравненияСкачать
Как решать квадратные уравнения. 8 класс. Вебинар | МатематикаСкачать
Как решать любое квадратное уравнение Полное Неполное квадр ур x^2+2x-3=0 5x^2-2x=0 2x^2-2=0 3x^2=0Скачать
Квадратное уравнение. 1 урок.Скачать
МАТЕМАТИКА 8 класс - Неполные Квадратные Уравнения. Как решать Неполные Квадратные Уравнения?Скачать
