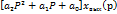Будем записывать однородное и неоднородное линейные дифференциальные уравнения в виде:
L(y) = 0 и L(y) = f(x).
Принцип суперпозиции основан на следующих свойствах решений линейных уравнений:
а) Если y1(x) и y2(x) — два решения однородного линейного уравнения L(y)=0, то их линейная комбинация y(x) = c1 y1(x) + c2 y2(x)
при любых постоянных c1, c2 является решением однородного уравнения.
б) Если y1(x) и y2(x) — два решения неоднородного линейного уравнения
L(y) = f(x), то их разность y(x) = y1(x) — y2(x)
является решением однородного уравнения L(y) = 0.
в) Любое решение неоднородного линейного уравнения L(y) = f(x) есть сумма частного (фиксированного) решения неоднородного уравнения и некоторого решения однородного уравнения.
ПРИМЕР 1. Проверка принципа суперпозиции для линейного дифференциального уравнения 2-го порядка.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Видео:Суперпозиция частных решений линейного неоднородного дифференциального уравненияСкачать
Метод суперпозиции в дифференциальных уравнениях
Рассмотрим линейное дифференциальное уравнение n –го порядка
основан на следующих
1. Если y 1( x ) и y 2( x )— два решения линейного однородного дифференциального уравнения
то любая их линейная комбинация y ( x ) = C 1 y 1( x ) + C 2 y 2( x ) является решением этого однородного уравнения.
2. Если y 1( x ) и y 2( x ) — два решения линейного неоднородного уравнения L ( y ) = f ( x ) , то их разность y ( x ) = y 1( x ) − y 2 ( x ) является решением однородного уравнения L ( y ) = 0 .
Видео:Принцип суперпозиции для линейных неоднородных дифференциальных уравнений.Скачать
Каким образом определяется линейная система управления
Каким образом определяется линейная система управления
Линейная динамическая система описывается линейными операторами – это операторы дифференцирования и интегрирования, для линейных систем присуще суперпозиции. Если на систему действует несколько возмущений, то выходная её реакция будет равна сумме реакции от каждого возмущения. Если на входе Х1 , то на выходе У1, если на входе Х2 . то на выходе У2. Х2 > Х1 , то У2 > У1. Если система не учитывает принцип суперпозиции, то система не линейна.
В чем состоит принцип суперпозиции линейной системы.
Линейные АСР описываются линейными дифференциальными уравнениями с постоянными коэффициентами. Линейные системы содержат только линейные элементы. Для линейных систем справедлив принцип суперпозиции; он заключается в том, что реакция системы на сумму любых внешних воздействий равна сумме реакций на каждое из этих воздействий, поданных на систему порознь. Принцип суперпозиции позволяет выразить реакцию системы на любое произвольное воздействие через реакцию системы на элементарное типовое воздействие, например в виде скачка. Для этого достаточно представить данное входное воздействие в виде совокупности выбранных типовых воздействий. На основе принципа суперпозиции разработана общая теория линейных автоматических систем регулирования, описываемых линейными дифференциальными уравнениями любого порядка.
Различие стационарных и нестационарных систем.
По поведению параметров системы во времени различают стационарные и нестационарные системы. Система называется стационарной, если ее реакция на любой тип возмущения зависит от интервала времени между данным моментом времени и моментом возмущения. Система называется нестационарной, если ее реакция на любой тип возмущения не зависит от интервала времени между данным моментом времени и моментом возмущения. Реакция стационарной системы на одно и то же возмущение не зависит от момента приложения этого возмущения.
Экспериментальный метод исследования систем управления: методика проведения активного и пассивного эксперимента.
Методы исследования: Области исследования подразделяются на экспериментальные и аналитические. Аналитические (во временной области, в частотной области, в области изображения). Экспериментальные делятся на активный эксперимент, который имеет типовые входные сигналы такие как ступенчатый, импульсивный и частотный, и пассивный. Пассивный эксперимент используется, когда не возможно нарушать ход технологического процесса, для этого регистрируют большое количество случайных входных величин и выходных, соответствующих входным. Достоинства – требует только регистрации сигналов.
Активный эксперимент используется, когда мы можем изменять входной сигнал объекта, а на выходе стоит регистратор сигнала. Ход проведения эксперимента: 1) стабилизируем часть посторонних возмущений, упрощая этим обработку эксперимента (убираем возмущения); 2) перед началом эксперимента устанавливаем равновесный режим системы (сигналы на входе и выходе постоянны); 3) выбираем величину и вид входного сигнала; 4) наносим возмущения и регистрируем входной и выходной сигналы.
Реакция системы автоматического управления при подаче типовых входных сигналов.
Методика получения передаточной функции из дифференциального уравнения АСР.
Дифференциальное уравнение системы:
Выполним преобразования по Лапласу.
Для этого произведем замену оператора дифференцирования.
→ p; y(t)→Y(p) (изображение); Х(t) → Х(р);
— уравнение записано в изображениях.
Дифференциальное уравнение преобразовали в алгебраическое.
или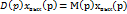 
;
D(p) – собственный оператор системы и характеризует её свободные колебания. М(р) – входной оператор, характеризует внешнее воздействие на систему (собственные колебательные системы). Отношение М(р) к D(p) называется передаточной функцией.
.
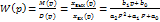
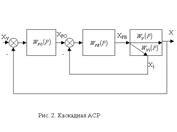
Каскадные АСР.
Каскадные системы применяются для объектов с большой инерционностью по каналу регулирования. Качество регулирования можно улучшить введением дополнительного контура стабилизации вспомогательной переменной.
Структура каскадной АСР представлена на рис.2. В системе действуют два регулятора – основной регулятор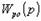 
, служащий для стабилизации основной регулируемой величины X, и вспомогательный регулятор 
,служащий для регулирования вспомогательной величины X1. При этом основной регулятор воздействует на изменение задания вспомогательному регулятору.
Расчет каскадной АСР предполагает определение настроек основного и вспомогательного регуляторов. Расчет настроек регуляторов осуществляют сведением многоконтурной АСР к одноконтурной путем введения определенных допущений.
Каким образом определяется линейная система управления
Линейная динамическая система описывается линейными операторами – это операторы дифференцирования и интегрирования, для линейных систем присуще суперпозиции. Если на систему действует несколько возмущений, то выходная её реакция будет равна сумме реакции от каждого возмущения. Если на входе Х1 , то на выходе У1, если на входе Х2 . то на выходе У2. Х2 > Х1 , то У2 > У1. Если система не учитывает принцип суперпозиции, то система не линейна.
📹 Видео
11. Уравнения в полных дифференциалахСкачать
Решение системы дифференциальных уравнений методом ЭйлераСкачать
Принцип суперпозиции в электричестве - bezbotvyСкачать
9. Метод вариации произвольной постоянной ( метод Лагранжа ). Линейные дифференциальные уравнения.Скачать
7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать
12. Интегрирующий множитель. Уравнения в полных дифференциалахСкачать
Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать
18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать
13. Как решить дифференциальное уравнение первого порядка?Скачать
19. Метод вариации произвольных постоянных. Линейные неоднородные диф уравнения 2-го порядкаСкачать
Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать
Принцип суперпозиции. Модель на осциллографеСкачать
16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать
Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать
Дифференциальные уравнения, 6 урок, Уравнения в полных дифференциалахСкачать
