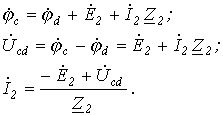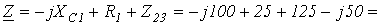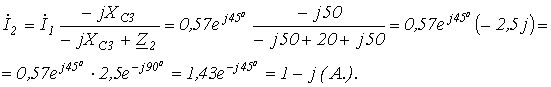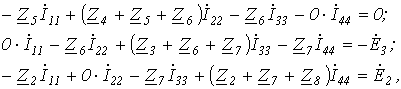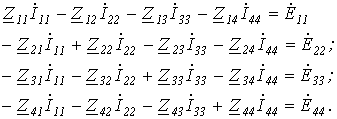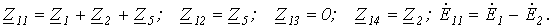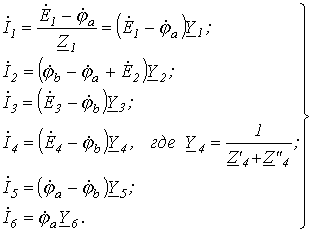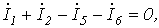Метод составления уравнений методом узловых потенциалов

При изучении основ электротехники приходится сталкиваться с необходимостью расчета тех или иных параметров различных схем. И самое простое, что приходится делать – это расчет токов ветвей в цепях постоянного тока.

Существует несколько наиболее применяемых методов расчетов для таких цепей: с помощью законов Кирхгофа, методом контурных токов, узловых потенциалов, методом эквивалентного генератора, эквивалентного источника тока, методом наложения. Для расчета более сложных цепей, например, в нелинейных схемах, могут применяться метод аппроксимации, графические методы и другие.
В данном разделе рассмотрим один из методов определения токов в цепи постоянного тока – метод узловых потенциалов.

Метод узловых потенциалов примеры решения задач

Для того, чтобы лучше разобраться в этом вопросе, рассмотрим конкретный пример схемы, показанной на рис.1.

Рис.1. Схема постоянного тока

Для начала обозначают направления токов в ветвях. Направление можно выбирать любым. Если в результате вычислений какой-то из токов получится с отрицательным значением, значит, его направление в действительности будет направлено в противоположную сторону относительно ранее обозначенного. Если в ветви имеется источник, то для удобства лучше обозначить направление тока в этой ветви совпадающим с направлением источника в этой ветви, хотя и не обязательно. Далее один из узлов схемы заземляем. Заземленный узел будет называться опорным, или базисным. Такой метод заземления на общее токораспределение в схеме влияния не оказывает.

Каждый из этих узлов будет обладать своим значением потенциала относительно узла 4. Именно значения этих потенциалов для дальнейшего определения токов и находят. Соответственно, для удобства этим потенциалам присваивают номера в соответствии с номером узла, т.е. φ₁, φ₂, φ₃. Далее составляется система уравнений для оставшихся узлов 1, 2, 3.

В общем виде система имеет вид:

Использованные в этой системе уравнений буквенно-цифровые обозначения

имеют следующий смысл:

– сумма проводимостей ветвей, сходящихся в узле 1. В данном случае

– сумма проводимостей ветвей, сходящихся в узле 2. В данном случае

– сумма проводимостей ветвей, сходящихся в узле 3. В данном случае

– сумма проводимостей ветвей, соединяющих узлы 1 и 2, взятая со знаком «минус». Для этого единица и взята с отрицательным знаком:

– сумма проводимостей ветвей, соединяющих узлы 1 и 3, взятая со знаком «минус». Для этого единица и в этом случае взята с отрицательным знаком:

Аналогично находятся и остальные проводимости:

J₁₁ – узловой ток узла 1, в котором участвуют ветви, подходящие именно к этому узлу, и содержащие в своем составе ЭДС. При этом, если ЭДС ветви, входящий в узел, направлена к рассматриваемому узлу (в данном случае к узлу 1), то такой узловой ток записывается с плюсом, если от узла, то с минусом. В данном случае

В результате всех ранее приведенных вычисленных значений исходная система уравнений примет вид:

Решать данную систему можно всеми доступными методами, мы же для упрощения решим ее в пакете Mathcad:

В результате получены следующие значения потенциалов в узлах цепи:

Токи в ветвях находятся в соответствии с законом Ома. Поясним это простыми словами.

В ветви с сопротивлением и источником, учитывая ранее обозначенное направление тока в рассматриваемой ветви, необходимо из потенциала узла, находящегося у начала стрелки направления тока, вычесть потенциал узла, находящегося у конца стрелки направления тока, а затем прибавить значение ЭДС в этой ветви. Далее все это разделить на сопротивление, имеющееся в ветви. Если бы ток и ЭДС в рассматриваемой ветви не совпадали по направлению, тогда значение ЭДС вычиталось. В ветви без ЭДС действует то же самое правило, только ЭДС в числителе, разумеется, отсутствует. В нашем примере получим, что

Значение тока первой ветви, как видно из расчета, получилось отрицательным. Значит, в действительности, этот ток направлен в противоположную сторону относительно его обозначенного направления на рис.1.

Правильность расчетов можно проверить, например, составлением баланса мощностей либо, к примеру, моделированием, схемы. Выполним моделирование в программе Multisim.

Рис.2. Моделирование в Multisim

Как видим, результаты моделирования совпадают с расчетными значениями. Незначительная разница в тысячных долях из-за округлений промежуточных вычислений.

1.4 Метод узловых потенциалов. Метод узлового напряжения (метод двух узлов)

1.4 Метод узловых потенциалов. Метод узлового напряжения (метод двух узлов)

В методе узловых потенциалов за вспомогательные расчетные величины принимают потенциалы узлов схемы. При этом потенциалом одного из узлов задаются, обычно считая его равным нулю (заземляют). Этот узел называют опорным узлом. Затем для каждого узла схемы, кроме опорного узла, составляют систему уравнений методом узловых потенциалов. По найденным потенциалам узлов находят токи ветвей по обобщенному закону Ома (закону Ома для ветви с ЭДС).

Отметим, что метод узловых потенциалов без предварительного преобразования схемы не применим к схемам с взаимной индукцией.

Для схем, содержащих несколько ветвей только с идеальными источниками ЭДС (без пассивных элементов), не имеющих общего узла нужно применять особые способы составления системы уравнений метода узловых потенциалов.

Для схем, содержащих несколько ветвей только с идеальными источниками ЭДС (без пассивных элементов), имеющих общий узел, этот общий узел принимают за опорный узел (заземляют). Тогда потенциалы узлов, соединенных этими идеальными источниками ЭДС без пассивных элементов с опорным узлом, равны ЭДС этих идеальных источников (+E, если идеальный источник ЭДС направлен от опорного узла и –E в противном случае).

Метод двух узлов является частным случаем метода узловых потенциалов. Он применяется для определения токов в ветвях схемы с двумя узлами и произвольным числом параллельных активных и пассивных ветвей.

Решение задач методом узловых потенциалов и методом двух узлов

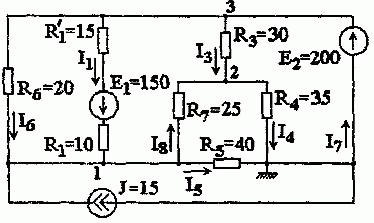
Задача 1.4.1 Рассчитать цепь рис. 1.4.1 методом узловых, потенциалов.

Решение. В рассматриваемой схеме четыре узла. Заземлим узел 4 (опорный узел)

φ 3 = φ 4 + E 2 = 200 B .

Необходимо найти потенциалы узлов 1 и 2. Составим систему уравнений по методу узловых потенциалов для узлов 1 и 2.

Рассматривая узел 1, получим

φ 1 ⋅ g 11 − φ 2 ⋅ g 12 − φ 3 ⋅ g 13 = J + E 1 R 1 + R ′ 1

φ 1 ⋅ g 11 − φ 2 ⋅ g 12 = J + E 1 R 1 + R ′ 1 + E 1 ⋅ g 13 .

В правой части этого уравнения оба слагаемых учтены со знаком плюс, так как J и E₁ направлены к узлу 1.

Рассматривая узел 2 (правая часть уравнения равна нулю, так как в ветвях, подсоединенных к узлу 2, нет источников энергии), получим

− φ 1 ⋅ g 21 + φ 2 ⋅ g 22 − φ 3 ⋅ g 23 = 0

− φ 1 ⋅ g 21 + φ 2 ⋅ g 22 = E 2 ⋅ g 23 .

Найдем собственную проводимость первого узла

g 11 = 1 R 6 + 1 R 1 + R ′ 1 + 1 R И Т + 1 R 2 + 1 R 5 = 1 20 + 1 25 + 1 25 + 1 40 = 0,155 С м .

Проводимость ветви с идеальным источником тока равна нулю, так как внутреннее сопротивление идеального источника тока R_ИТ равно бесконечности.

Собственная проводимость узла 2

g 22 = 1 R 2 + 1 R 3 + 1 R 4 = 1 25 + 1 30 + 1 35 = 0,102 С м .

Взаимные проводимости между узлами

g 13 = 1 R 6 + 1 R 1 + R ′ 1 = 1 20 + 1 25 = 0,09 С м ; g 21 = g 12 = 1 R 2 = 1 25 = 0,04 С м ; g 23 = 1 R 3 = 1 30 = 0,033 С м .

Подставив в уравнения известные величины, получим

Для решения этой системы используем метод определителей. Главный определитель системы

Δ = | 0,155 − 0,04 − 0,04 0,102 | = 0,01421.

Δ 1 = | 39 − 0,04 6,6 0,102 | = 4,242 ; Δ 2 = | 0,155 39 − 0,04 6,6 | = 2,583.

Находим потенциалы узлов

φ 1 = Δ 1 Δ = 4,242 0,01421 = 298,6 В ; φ 2 = Δ 2 Δ = 2,583 0,01421 = 181,8 В .

Определяем токи в ветвях (положительные направления токов в ветвях с ЭДС выбираем по направлению ЭДС, в остальных ветвях произвольно)

I 1 = φ 3 − φ 1 + E 1 R 1 + R ′ 1 = 200 − 298,6 + 150 10 + 15 = 2,056 А .

В числителе этого выражения от потенциала узла 3, из которого вытекает ток I₁, вычитается потенциал узла 1, к которому ток подтекает. Если ЭДС ветви совпадает (не совпадает) с выбранным направлением тока, то она учитывается со знаком плюс (минус). В знаменателе выражения учитываются сопротивления ветви.

Аналогично определяем другие токи (направления токов указаны на схеме рис. 1.4.1)

I 1 = φ 3 − φ 1 R 6 = 200 − 298,6 20 = − 4,93 А ; I 2 = φ 1 − φ 2 R 2 = 298,6 − 181,8 25 = 4,67 А ; I 3 = φ 3 − φ 2 R 3 = 200 − 181,8 30 = 0,607 А ; I 4 = φ 2 − φ 4 R 4 = 181,8 − 0 35 = 5,194 А .

Для определения тока в ветви с идеальной ЭДС зададимся направлением тока I₇. По первому закону Кирхгофа для узла 3 составим уравнение

− I 7 + I 3 + I 1 + I 6 = 0.

I 7 = I 3 + I 1 + I 6 = 0,607 + 2,056 − 4,98 = − 2,317 A .

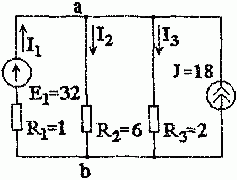
Задача 1.4.2 Определить токи в схеме рис. 1.4.2 методом узлового напряжения.

1 Находим напряжение между двумя узлами по методу двух узлов

U a b = φ a − φ b = E 1 ⋅ g 1 + J g 1 + g 2 + g 3 = 32 ⋅ 1 1 + 18 1 1 + 1 6 + 1 2 = 30 B .

При составлении этого уравнения по методу двух узлов в числителе необходимо брать произведение ЭДС на проводимость своей ветви со знаком плюс, если ЭДС направлена к узлу a, и минус – если направлена от узла a к узлу b.

Аналогичное правило определяет и знаки токов источников тока.

2 Находим токи по закону Ома (по закону Ома для ветви с ЭДС)

I 1 = E 1 + φ b − φ a R 1 = E 1 − U a b R 1 = 32 − 30 1 = 2 А ; I 2 = U a b R 2 = 30 6 = 5 А ; I 3 = U a b R 3 = 30 2 = 15 А .

Правильность решения проверим по первому закону Кирхгофа

I 1 − I 2 + I 3 + J = 0 ; 2 − 5 − 15 + 18 = 0.

взаимная проводимость, собственная проводимость, метод узловых потенциалов, метод узловых напряжений, метод двух узлов, опорный узел

Основы символического метода расчета. Методы контурных токов и узловых потенциалов.

Закон Ома для участка цепи с источником ЭДС

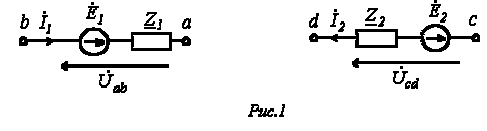Возьмем два участка цепи a — b и c — d (см. рис. 1) и составим для них уравнения в комплексной форме с учетом указанных на рис. 1 положительных направлений напряжений и токов.

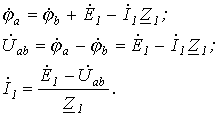
Объединяя оба случая, получим

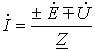(1)

или для постоянного тока

.

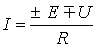(2)

Формулы (1) и (2) являются аналитическим выражением закона Ома для участка цепи с источником ЭДС , согласно которому ток на участке цепи с источником ЭДС равен алгебраической сумме напряжения на зажимах участка цепи и ЭДС, деленной на сопротивление участка. В случае переменного тока все указанные величины суть комплексы. При этом ЭДС и напряжение берут со знаком “+”, если их направление совпадает с выбранным направлением тока, и со знаком “-”, если их направление противоположно направлению тока.

Основы символического метода расчета цепей
синусоидального тока

Расчет цепей переменного синусоидального тока может производиться не только путем построения векторных диаграмм, но и аналитически – путем операций с комплексами, символически изображающими синусоидальные ЭДС, напряжения и токи. Достоинством векторных диаграмм является их наглядность, недостатком – малая точность графических построений. Применение символического метода позволяет производить расчеты цепей с большой степенью точности.

Символический метод расчета цепей синусоидального тока основан на законах Кирхгофа и законе Ома в комплексной форме.

Уравнения, выражающие законы Кирхгофа в комплексной форме, имеют совершенно такой же вид, как и соответствующие уравнения для цепей постоянного тока. Только токи, ЭДС, напряжения и сопротивления входят в уравнение в виде комплексных величин.

1. Первый закон Кирхгофа в комплексной форме:

.

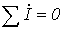(3)

2. Второй закон Кирхгофа в комплексной форме:

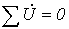(4)

или применительно к схемам замещения с источниками ЭДС

.

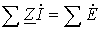(5)

3. Соответственно матричная запись законов Кирхгофа в комплексной форме имеет вид:

§ первый закон Кирхгофа:

. ;

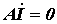(6)

§ второй закон Кирхгофа

.

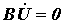(7)

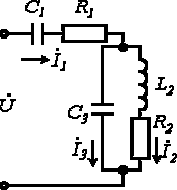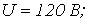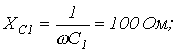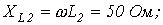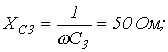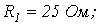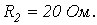	Определить:	1) полное комплексное сопротивление цепи ;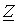
		2) токи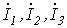
Рис. 2

1. .

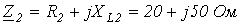
2. .

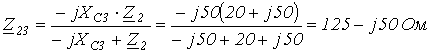
3.

.

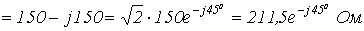
4. Принимая начальную фазу напряжения за нуль, запишем:

.

.

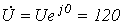
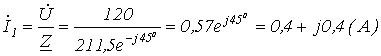
5. Поскольку ток распределяется обратно пропорционально сопротивлению ветвей (это вытекает из закона Ома), то

6. .

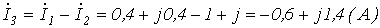
7. Аналогичный результат можно получить, составив для данной схемы уравнения по законам Кирхгофа в комплексной форме

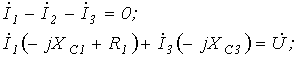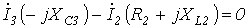или после подстановки численных значений параметров схемы

Специальные методы расчета

Режим работы любой цепи полностью характеризуется уравнениями, составленными на основании законов Кирхгофа. При этом необходимо составить и решить систему с n неизвестными, что может оказаться весьма трудоемкой задачей при большом числе n ветвей схемы. Однако, число уравнений, подлежащих решению, может быть сокращено, если воспользоваться специальными методами расчета , к которым относятся методы контурных токов и узловых потенциалов.

Метод контурных токов

Идея метода контурных токов: уравнения составляются только по второму закону Кирхгофа, но не для действительных, а для воображаемых токов, циркулирующих по замкнутым контурам, т.е. в случае выбора главных контуров равных токам ветвей связи. Число уравнений равно числу независимых контуров, т.е. числу ветвей связи графа 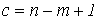. Первый закон Кирхгофа выполняется автоматически. Контуры можно выбирать произвольно, лишь бы их число было равно и чтобы каждый новый контур содержал хотя бы одну ветвь, не входящую в предыдущие. Такие контуры называются независимыми . Их выбор облегчает использование топологических понятий дерева и ветвей связи.

Направления истинных и контурных токов выбираются произвольно. Выбор положительных направлений перед началом расчета может не определять действительные направления токов в цепи. Если в результате расчета какой-либо из токов, как и при использовании уравнений по законам Кирхгофа, получится со знаком “-”, это означает, что его истинное направление противоположно.

Пусть имеем схему по рис. 3.

Выразим токи ветвей через контурные токи:

;

; ;

; .

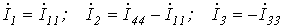
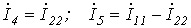
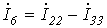
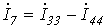
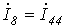
Обойдя контур aeda, по второму закону Кирхгофа имеем

.

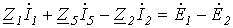
Поскольку ,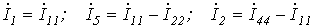

.

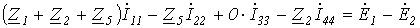
Таким образом, получили уравнение для первого контура относительно контурных токов. Аналогично можно составить уравнения для второго, третьего и четвертого контуров:

совместно с первым решить их относительно контурных токов и затем по уравнениям, связывающим контурные токи и токи ветвей, найти последние.

Однако данная система уравнений может быть составлена формальным путем:

При составлении уравнений необходимо помнить следующее:

— сумма сопротивлений, входящих в i- й контур;

— сумма сопротивлений, общих для i- го и k- го контуров, причем ;

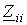
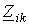
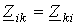
члены на главной диагонали всегда пишутся со знаком “+”;

знак “+” перед остальными членами ставится в случае, если через общее сопротивление 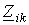i- й и k- й контурные токи проходят в одном направлении, в противном случае ставится знак “-”;

если i- й и k- й контуры не имеют общих сопротивлений, то ;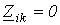

в правой части уравнений записывается алгебраическая сумма ЭДС, входящих в контур: со знаком “+”, если направление ЭДС совпадает с выбранным направлением контурного тока, и “-”, если не совпадает.

В нашем случае, для первого уравнения системы, имеем:

Следует обратить внимание на то, что, поскольку 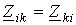, коэффициенты контурных уравнений всегда симметричны относительно главной диагонали.

Если в цепи содержатся помимо источников ЭДС источники тока, то они учитываются в левых частях уравнений как известные контурные токи: k- й контурный ток, проходящий через ветвь с k- м источником тока равен этому току .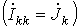

Метод узловых потенциалов

Данный метод вытекает из первого закона Кирхгофа. В качестве неизвестных принимаются потенциалы узлов, по найденным значениям которых с помощью закона Ома для участка цепи с источником ЭДС затем находят токи в ветвях. Поскольку потенциал – величина относительная, потенциал одного из узлов (любого) принимается равным нулю. 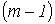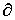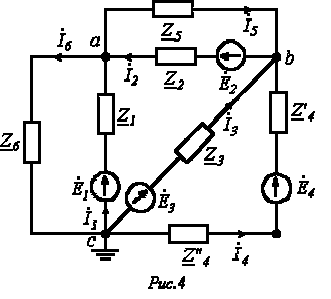Таким образом, число неизвестных потенциалов, а следовательно, и число уравнений равно , т.е. числу ветвей дерева .

Пусть имеем схему по рис. 4, в которой примем .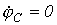

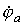
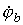
Допустим, что и известны. Тогда значения токов на основании закона Ома для участка цепи с источником ЭДС

Запишем уравнение по первому закону Кирхгофа для узла а :

и подставим значения входящих в него токов, определенных выше:

.

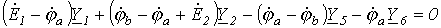
Сгруппировав соответствующие члены, получим:

.

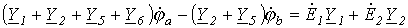
Аналогично можно записать для узла b :

.

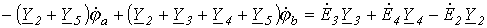
Как и по методу контурных токов, система уравнений по методу узловых потенциалов может быть составлена формальным путем. При этом необходимо руководствоваться следующими правилами:

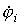
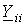
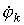
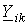
1. В левой части i- го уравнения записывается со знаком “+”потенциал i- го узла, для которого составляется данное i- е уравнение, умноженный на сумму проводимостей ветвей, присоединенных к данному i- му узлу, и со знаком “-”потенциал соседних узлов, каждый из которых умножен на сумму проводимостей ветвей, присоединенных к i- му и k- му узлам.

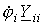
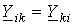
Из сказанного следует, что все члены , стоящие на главной диагонали в левой части системы уравнений, записываются со знаком “+”, а все остальные – со знаком “-”, причем . Последнее равенство по аналогии с методом контурных токов обеспечивает симметрию коэффициентов уравнений относительно главной диагонали.

2. В правой части i- го уравнения записывается так называемый узловой ток 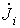, равный сумме произведений ЭДС ветвей, подходящих к i- му узлу, и проводимостей этих ветвей. При этом член суммы записывается со знаком “+”, если соответствующая ЭДС направлена к i- му узлу, в противном случае ставится знак “-”. Если в подходящих к i- му узлу ветвях содержатся источники тока, то знаки токов источников токов, входящих в узловой ток простыми слагаемыми, определяются аналогично.

В заключение отметим, что выбор того или иного из рассмотренных методов определяется тем, что следует найти, а также тем, какой из них обеспечивает меньший порядок системы уравнений. При расчете токов при одинаковом числе уравнений предпочтительнее использовать метод контурных токов, так как он не требует дополнительных вычислений с использованием закона Ома. Метод узловых потенциалов очень удобен при расчетах многофазных цепей, но не удобен при расчете цепей со взаимной индуктивностью.

1. Основы теории цепей: Учеб.для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.

2. Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.

Контрольные вопросы и задачи

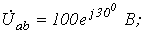
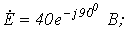
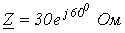
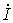
1. В ветви на рис. 1 . Определить ток .

Ответ: .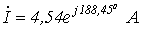

2. В чем заключается сущность символического метода расчета цепей синусоидального тока?

3. В чем состоит сущность метода контурных токов?

4. В чем состоит сущность метода узловых потенциалов?

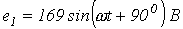
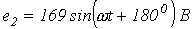
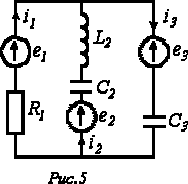
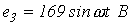
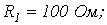
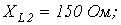
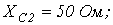
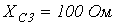
5. В цепи на рис. 5 ; ; ; . Методом контурных токов определить комплексы действующих значений токов ветвей.

Ответ: ; ; .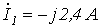

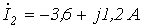
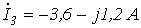
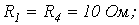
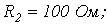
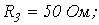
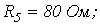
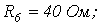
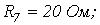
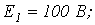
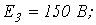
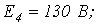
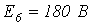
6. В цепи на рис. 6 . Рассчитать токи в ветвях, используя метод узловых потенциалов.

Ответ: ; ; ; ; ; ; .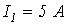

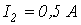
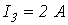
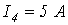
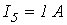
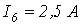
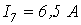
🔥 Видео