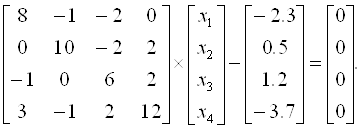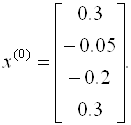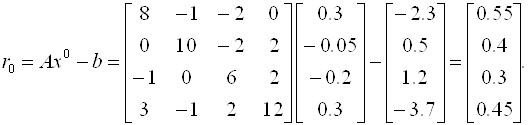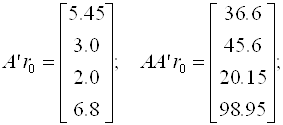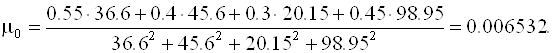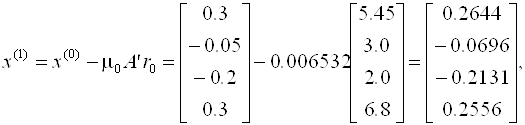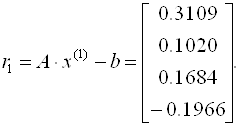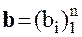Видео:Решение системы уравнений методом ГауссаСкачать

Безусловная оптимизация. Метод наискорейшего спуска
Метод наискорейшего спуска (в англ. литературе «method of steepest descent») — это итерационный численный метод (первого порядка) решения оптимизационных задач, который позволяет определить экстремум (минимум или максимум) целевой функции:

В соответствии с рассматриваемым методом экстремум (максимум или минимум) целевой функции определяют в направлении наиболее быстрого возрастания (убывания) функции, т.е. в направлении градиента (антиградиента) функции. Градиентом функции в точке 
где i, j,…, n — единичные векторы, параллельные координатным осям.
Градиент в базовой точке 
Метод наискорейшего спуска является дальнейшим развитием метода градиентного спуска. В общем случае процесс нахождения экстремума функции является итерационной процедурой, которая записывается следующим образом:
где знак «+» используется для поиска максимума функции, а знак «-» используется для поиска минимума функции;



Величина шага выбирается из условия минимума целевой функции f(х) в направлении движения, т. е. в результате решения задачи одномерной оптимизации в направлении градиента или антиградиента:
Другими словами, величину шага 
Таким образом, шаг расчета выбирается такой величины, что движение выполняется до тех пор, пока происходит улучшение функции, достигая, таким образом, экстремума в некоторой точке. В этой точке вновь определяют направление поиска (с помощью градиента) и ищут новую точку оптимума целевой функции и т.д. Таким образом, в данном методе поиск происходит более крупными шагами, и градиент функции вычисляется в меньшем числе точек.
В случае функции двух переменных данный метод имеет следующую геометрическую интерпретацию: направление движения из точки 

Рис.1. Траектория движения к точке экстремума при использовании метода наискорейшего спуска, изображенная на графике линии равного уровня функции f(x)
Поиск оптимального решения завершается в случае, когда на итерационном шаге расчета (несколько критериев):
— траектория поиска остается в малой окрестности текущей точки поиска:
— приращение целевой функции не меняется:
— градиент целевой функции в точке локального минимума обращается в нуль:
Следует отметить, что метод градиентного спуска оказывается очень медленным при движении по оврагу, причём при увеличении числа переменных целевой функции такое поведение метода становится типичным. Овраг представляет собой впадину, линии уровня которой приближенно имеют форму эллипсов с различающимися во много раз полуосями. При наличии оврага траектория спуска имеет вид зигзагообразной линии с малым шагом, вследствие чего результирующая скорость спуска к минимуму сильно замедляется. Это объясняется тем, что направление антиградиента этих функций существенно отклоняется от направления в точку минимума, что приводит к дополнительной задержке в расчете. В результате алгоритм теряет вычислительную эффективность.
Метод градиента вместе с его многочисленными модификациями является распространенным и эффективным методом поиска оптимума исследуемых объектов. Недостатком градиентного поиска (так же и рассмотренных выше методов) является то, что при его использовании можно обнаружить только локальный экстремум функции. Для отыскания других локальных экстремумов необходимо производить поиск из других начальных точек. Так же скорость сходимости градиентных методов существенно зависит также от точности вычислений градиента. Потеря точности, а это обычно происходит в окрестности точек минимума или в овражной ситуации, может вообще нарушить сходимость процесса градиентного спуска.
Методика расчета
• 1 шаг: Определение аналитические выражения (в символьном виде) для вычисления градиента функции
• 2 шаг: Задаем начальное приближение
Далее выполняется итерационный процесс.
• 3 шаг: Определяется необходимость рестарта алгоритмической процедуры для обнуления последнего направления поиска. В результате рестарта поиск осуществляется заново в направлении скорейшего спуска.
• 4 шаг: Вычисление координат единичного вектора 
• 5 шаг: определяем шаг расчета из условия поиска экстремума для следующей функции 
• 6 шаг: Определяем новые значения аргументов функции после выполнения k-го шага расчета:
где знак «+» используется для поиска максимума функции, а знак «-» используется для поиска минимума функции;
• 7 шаг: проверяем критерии останова итерационного процесса. Вычислительный процесс заканчивается, когда будет достигнута точка, в которой оценка градиента будет равна нулю (коэффициенты функции отклика становятся незначимыми). В противном случае возвращаемся к шагу 3 и продолжаем итерационный расчет.
Для того, чтобы добавить Ваш комментарий к статье, пожалуйста, зарегистрируйтесь на сайте.
Видео:Метод покоординатного спускаСкачать

3.8. Метод скорейшего спуска (градиента) для случая . системы линейных алгебраических уравнений
В рассматриваемом ниже итерационном методе вычислительный алгоритм строится таким образом, чтобы обеспечить минимальную погрешность на шаге (максимально приблизиться к корню).
Представим систему линейных уравнений в следующем виде:
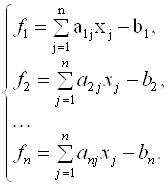
Запишем выражение (3.38) в операторной форме:
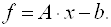
Здесь приняты следующие обозначения:
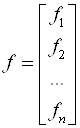
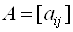

В методе скорейшего спуска решение ищут в виде
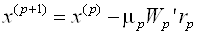
Где 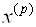
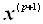
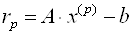
А 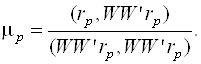
В формуле (3.43) используется скалярное произведение двух векторов, которое определяется следующей формулой:
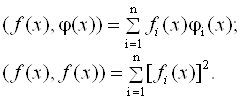
В формуле (3.43) 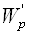

Нетрудно убедиться, что для системы (3.39) матрица Якоби равна

Как и для метода простой итерации, достаточным условием сходимости метода градиента является преобладание диагональных элементов. В качестве нулевого приближения можно взять 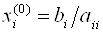
· Как видно из выражения (3.45), матрица Якоби не зависит от шага итерации.
· Требования минимизации погрешности на каждом шаге обусловили то, что метод градиента более сложен (трудоемок), чем методы Якоби и Зейделя.
· В методе градиента итерационный процесс естественно закончить при достижении 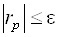
· В приближенных методах можно обеспечить практически любую погрешность, если итерационный процесс сходится.
· Итерационный процесс можно прервать на любом K–ом шаге и продолжить позднее, введя в качестве нулевого шага значения X(K).
· В качестве недостатка приближенных методов можно отметить то, что они часто расходятся, достаточные условия сходимости (преобладание диагональных элементов) можно обеспечить только для небольших систем из 3 – 6 уравнений.
Пример 3.7. Методом скорейшего спуска решим систему уравнений
Так как диагональные элементы матрицы являются преобладающими, то в качестве начального приближения выберем:
Следовательно, вектор невязок на нулевом шаге равен
Далее последовательно вычисляем
Отсюда
Аналогично находятся последующие приближения и оцениваются невязки. Что касается данного примера, можно отметить, что итерационный процесс сходится достаточно медленно (невязки уменьшаются).
Вопросы для самопроверки
· Назовите известные вам методы решения СЛАУ.
· Чем точные методы отличаются от приближенных?
· Что такое прямой и обратный ход в методе Гаусса?
· Нужен ли обратный ход при вычислении методом Гаусса а) обратной матрицы; б) определителя?
· Что такое невязка?
· Сравните достоинства и недостатки точных и приближенных методов.
· Что такое матрица Якоби?
· Надо ли пересчитывать матрицу Якоби на каждом шаге итерации в методе градиента?
· Исходная СЛАУ решается независимо тремя методами – методом Якоби, методом Зейделя и методом градиента. Будут ли равны значения
А) начального приближения (нулевой итерации);
Б) первой итерации?
· При решении СЛАУ (n > 100) итерационными методами решение расходится. Как найти начальное приближение?
Видео:Градиентный метод | метод скорейшего спуска + примерСкачать

Решение систем линейных алгебраических уравнений
Страницы работы
Содержание работы
Лабораторная работа №3
Решение систем линейных алгебраических уравнений
Практика использования итерационных методов решения системы линейных алгебраических уравнений. Сравнительный анализ методов.
Решить систему линейных алгебраических уравнений (САУ)
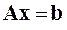
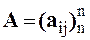
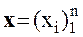
итерационными методами Зейделя и наискорейшего спуска с точностью до e = 0,001. Для сравнения с истинными значениями корней выполнить решение указанной САУ методом Гаусса.
Общий вид алгоритма Зейделя и наискорейшего спуска
Метод Зейделя заключается в том, что найденное на 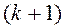
Расчетные соотношения метода Зейделя для подготовленной системы уравнений (4.13) имеют вид
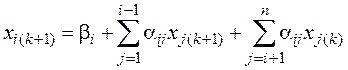
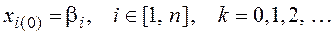
При составлении программы для вычислений на ЭВМ вместо соотношения (4.18) удобнее использовать выражение, в котором фигурируют элементы исходной системы уравнений
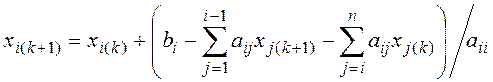
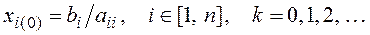
Если матрица 
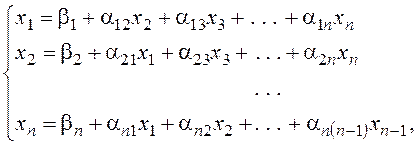
где 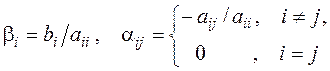


Из неособенной матрицы 

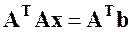
Метод наискорейшего спуска. Данный метод относится к группе нелинейных градиентных алгоритмов. Градиентные алгоритмы, уточнение решения в которых осуществлялось по отдельным координатам, предполагают траекторию движения к истинному решению сразу по всем координатам по линии наискорейшего спуска в направлении, противоположном вектору градиента функционала, связанного с ошибкой между истинным решением и решением на 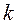
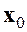
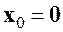
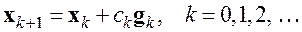
где 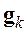
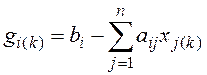
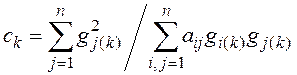
Чтобы упростить процедуру определения вектора невязки, особенно при больших порядках 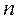
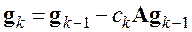
Однако из-за наличия вычислительных погрешностей векторы 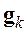
Если матрица 
SUBROUTINE N1YMGS (A,B,N,G,X),
SUBROUTINE N1YMNS (A,B,N,G,X)
реализуют алгоритмы решения САУ методами Зейделя и наискорейшего спуска (одна итерация) соответственно.
Входные параметры подпрограмм:
А(N,N) — (N ´ N)-мерная матрица САУ;
B(N) — N-мерный вектор правой части САУ;
N — мерность САУ;
G(N) — N-мерный вектор невязки (g = b — Ax);
X(N) — N-мерный вектор начальных условий решения САУ.
Выходные параметры подпрограммы:
X(N) — N-мерный вектор уточненных значений решения САУ.
Окончание итерационной процедуры производиться при выполнении условия 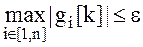
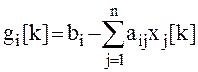
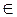
SUBROUTINE N1YGAU (A,B,X,N)
реализует алгоритм метода Гаусса с выбором главного элемента.
Входные A, B, N и выходной X параметры подпрограммы N1YGAU совпадают по описанию с аналогичными параметрами в подпрограммах N1YMGS, N1YMNS.
В подпрограмме N1YGAU матрица A приводится к треугольной.
🎦 Видео
Решение систем уравнений методом подстановкиСкачать

Решение систем уравнений методом сложенияСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

9 класс, 11 урок, Методы решения систем уравненийСкачать

Решение систем уравнений методом сложенияСкачать

Графический способ решения систем уравнений. Алгебра, 9 классСкачать

Система уравнений. Метод алгебраического сложенияСкачать

Метод наискорейшего спуска (Градиентного) - ВизуализацияСкачать

Градиентный спуск на пальцахСкачать

ЦОС Python #2: Метод градиентного спускаСкачать

ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод ПодстановкиСкачать

Математика | Система уравнений на желтую звездочку (feat Золотой Медалист по бегу)Скачать

6 способов в одном видеоСкачать

Лекция 2.4: Градиентный спуск.Скачать

Лекция 15. Метод скорейшего спуска. Argmin и его свойства. Идея метода. Скорость обученияСкачать

Метод наискорейшего спускаСкачать

Решение системы линейных уравнений графическим методом. 7 класс.Скачать