Метод скорейшего спуска для систем нелинейных уравнений (7 видео)

Содержание

Julia, Градиентный спуск и симплекс метод
Метод градиентного спуска
Симплекс метод
5.2. Метод градиента (метод скорейшего спуска)
Метод градиента (метод скорейшего спуска) для случая системы нелинейных уравнений
курсач.doc
🎥 Видео

Видео:После этого видео, ТЫ РЕШИШЬ ЛЮБУЮ Систему Нелинейных УравненийСкачать

Julia, Градиентный спуск и симплекс метод

Продолжаем знакомство с методами многомерной оптимизации.

Далее предложена реализация метода наискорейшего спуска с анализом скорости выполнения, а также имплементация метода Нелдера-Мида средствами языка Julia и C++.

Видео:Способы решения систем нелинейных уравнений. 9 класс.Скачать

Метод градиентного спуска

Поиск экстремума ведется шагами в направлении градиента (max) или антиградиента (min). На каждом шаге в направлении градиента (антиградиента) движение осуществляется до тех пор, пока функция возрастает (убывает).

За теорией пройдитесь по ссылкам:

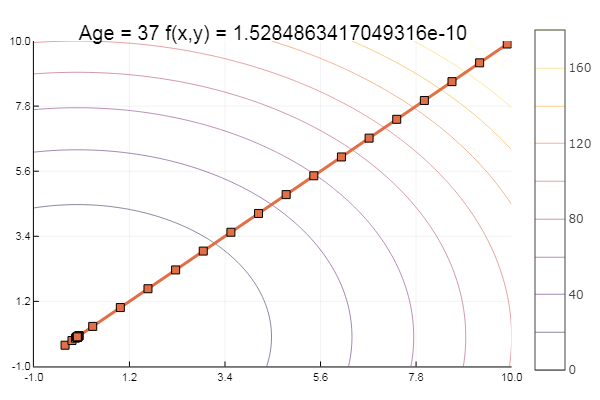
Модельной функцией выберем эллиптический параболоид и зададим функцию отрисовки рельефа:

Зададим функцию реализующую метод наискорейшего спуска, которая принимает размерность задачи, точность, длину шага, начальное приближение и размеры рамки ограничивающей график:

На функции вычисляющей направление градиента можно заостриться в плане оптимизации.

Первое, что идет на ум — это действия с матрицами:

Чем действительна хороша Julia, так это тем, что проблемные места легко можно потестить:

Можно кинуться перепечатывать всё в Сишном стиле

Но как оказывается, оно само и без нас знает, какие типы надо ставить, так что приходим к компромиссу:

А теперь пусть рисует:

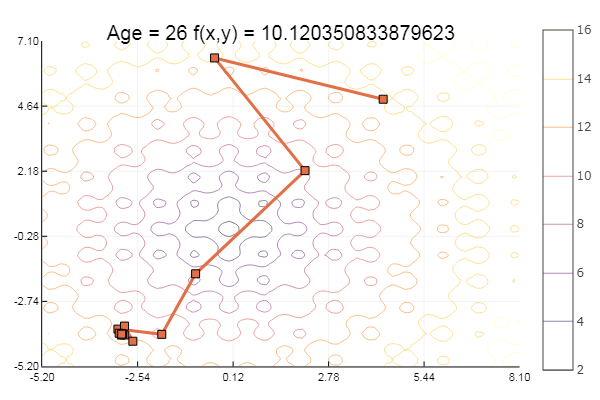
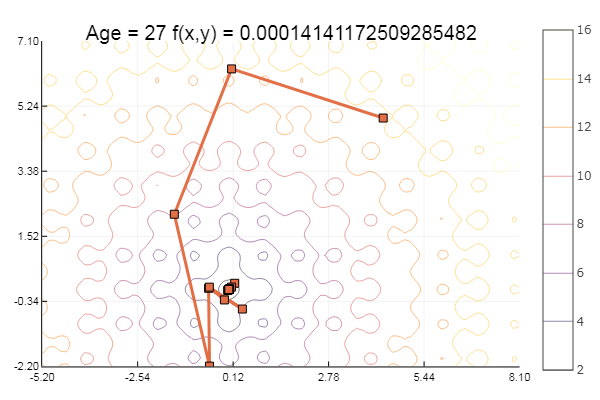
А теперь опробуем на функции Экли:

Свалилось в локальный минимум. Сделаем-ка шаги побольше:

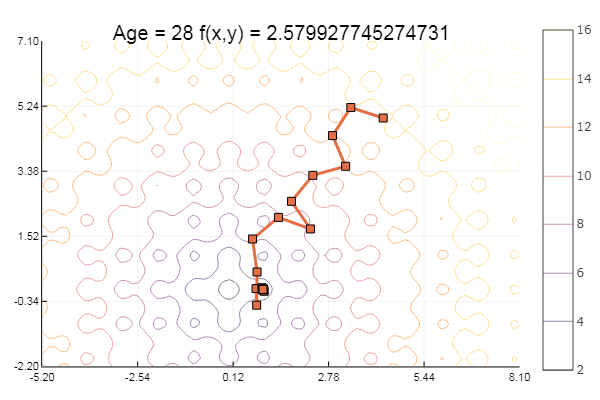
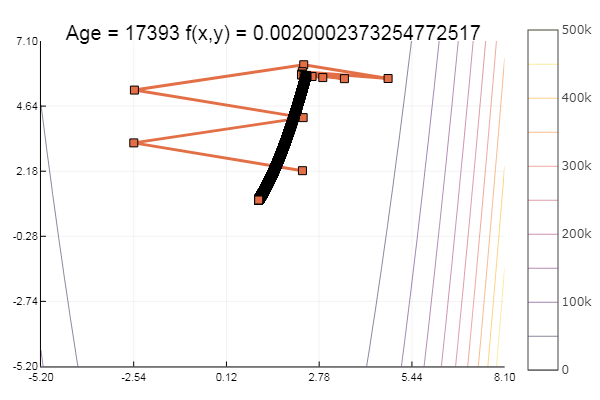
Отлично! А теперь что-нибудь с оврагом, например функцию Розенброка:

Мораль: градиенты не любят пологостей.

Видео:Способы решения систем нелинейных уравнений. Практическая часть. 9 класс.Скачать

Симплекс метод

Метод Нелдера — Мида, также известный как метод деформируемого многогранника и симплекс-метод, — метод безусловной оптимизации функции от нескольких переменных, не использующий производной(точнее — градиентов) функции, а поэтому легко применим к негладким и/или зашумлённым функциям.

Суть метода заключается в последовательном перемещении и деформировании симплекса вокруг точки экстремума.

Метод находит локальный экстремум и может «застрять» в одном из них. Если всё же требуется найти глобальный экстремум, можно пробовать выбирать другой начальный симплекс.

И сам симплекс метод:

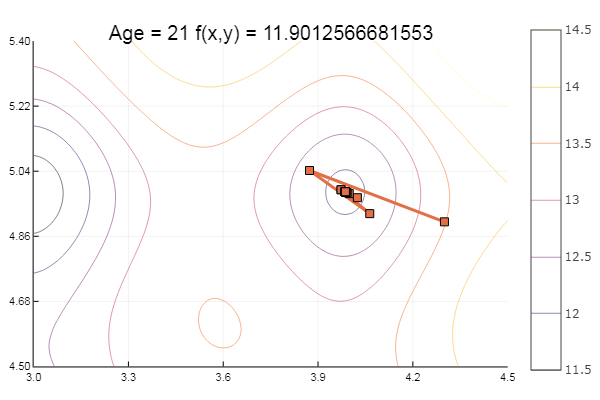
И на десерт какую-нибудь буку… например функцию Букина

Локальный минимум — ну ничего, главное правильно подобрать стартовый симплекс, так что для себя я нашел фаворита.

Бонус. Методы Нелдера-Мида, наискорейшего спуска и покоординатного спуска на С++

На сегодня достаточно. Следующим этапом будет логично попробовать что-нибудь из глобальной оптимизации, набрать побольше тестовых функций, а затем изучить пакеты со встроенными методами.

Видео:Метод простых итераций пример решения нелинейных уравненийСкачать

5.2. Метод градиента (метод скорейшего спуска)

Пусть имеется система нелинейных уравнений:

(5.13)

Систему (5.13) удобнее записать в матричном виде:

(5.14)

Где — вектор – функция; — вектор – аргумент.

Решение системы (5.14), как и для системы линейных уравнений (см. п. 3.8), будем искать в виде

(5.15)

Здесь и — векторы неизвестных на P и P+1 шагах итераций; вектор невязок на P-ом шаге – F(P) = F(X(P)); W‘P – транспонированная матрица Якоби на P – ом шаге;

;

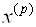
Пример 5.2. Методом градиента вычислим приближенно корни системы

Расположенные в окрестности начала координат.

Выберем начальное приближение:

По вышеприведенным формулам найдем первое приближение:

Аналогичным образом находим следующее приближение:

Ограничимся двумя итерациями (шагами), и оценим невязку:

· Как видно из примера, решение достаточно быстро сходится, невязка быстро убывает.

· При решении системы нелинейных уравнений методом градиента матрицу Якоби необходимо пересчитывать на каждом шаге (итерации).

Вопросы для самопроверки

· Как найти начальное приближение: а) для метода Ньютона; б) для метода градиента?

· В методе скорейшего спуска вычисляется Якобиан (матрица Якоби). Чем отличается Якобиан, вычисленный для СЛАУ, от Якобиана, вычисленного для нелинейной системы уравнений?

· Каков критерий остановки итерационного процесса при решении системы нелинейных уравнений: а) методом Ньютона; б) методом скорейшего спуска?

Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать

Метод градиента (метод скорейшего спуска) для случая системы нелинейных уравнений

Автор работы: Пользователь скрыл имя, 30 Ноября 2013 в 13:35, курсовая работа

Краткое описание

В настоящее время не существует методов, которые в одинаковой мере были бы хороши для всех систем ЛАУ. Почти все методы являются ориентированными и учитывают тем или иным образом специальные свойства матриц систем ЛАУ.
В курсовом проекте я рассматриваю метод скорейшего спуска. Этот метод не входит в число методов, которые широко используются и часто встречаются в литературе. Он реже используется в практике вычислений, но тем не менее содержит глубокие идеи и входит в основы теории вычислительной алгебры.

Содержание

Введение………………………………………………………. 2
1. Метод градиента (метод скорейшего спуска) для случая системы нелинейных уравнений……………………….……….3
2. Метод скорейшего спуска для случая системы линейных уравнений…………………………………………………………..11
3. Свойства приближений метода скорейшего спуска……17
Заключение……….………….…………………………………25
Список использованной литературы…………

Прикрепленные файлы: 1 файл

Видео:МЗЭ 2021 Лекция 11 Метод Ньютона для решения систем нелинейных уравненийСкачать

курсач.doc

1. Метод градиента (метод скорейшего спуска) для случая системы нелинейных уравнений……………………….……….3

2. Метод скорейшего спуска для случая системы линейных уравнений……………………………… …………………………..11

3. Свойства приближений метода скорейшего спуска……17

Список использованной литературы…………….………….26

Задачи численного решения систем линейных алгебраических уравнений (ЛАУ) и систем нелинейных численных уравнений многочисленны и весьма разнообразны. Это в первую очередь объясняется многообразием матриц систем ЛАУ и просто матриц для которых необходимо проводить вычисления.

В курсовом проекте я рассматриваю метод скорейшего спуска. Этот метод не входит в число методов, которые широко используются и часто встречаются в литературе. Он реже используется в практике вычислений, но тем не менее содержит глубокие идеи и входит в основы теории вычислительной алгебры.

Метод градиента (метод скорейшего спуска) для случая системы нелинейных уравнений.

Пусть имеется система нелинейных уравнений:

Систему (1) удобнее записать в матричном виде:

где — вектор – функция; — вектор – аргумент.

Предположим, что функции действительны и непрерывно дифференцируемы в их общей области определения. Рассмотрим функцию:

Очевидно, что каждое решение системы (1) обращает в нуль функцию U(x); наоборот, числа x₁, x₂, . x_n, для которых функция U(x) равна нулю, являются корнями системы (1).

Будем предполагать, что система (1) имеет лишь изолированное решение, которое представляет собой точку строгого минимума функции U(x). Таким образом, задача сводится к нахождению минимума функции U(x) в n-мерном пространстве

Пусть x – вектор-корень системы (1) и x (0) – его нулевое приближение. Через точку x (0) проведем поверхность уровня функции U(x). Если точка x (0) достаточна близка к корню х, то при наших предположениях поверхность уровня

будет похожа на эллипсоид.

Из точки х (0) двигаемся по нормали к поверхности U(x)=U(x (0) ) до тех пор, пока эта нормаль не коснется в некоторой точке х (1) какой-то другой поверхности уровня.