Метод сканирования для решения уравнений (5 видео)

4.1. Метод сканирования

Метод заключается в последовательном переборе всех значений 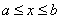С шагом  (погрешность решения) с вычислением критерия оптимальности F в каждой точке. Путем выбора наибольшего из всех вычислений значений F и находится решение задачи Х*.

Достоинство метода в том, что можно найти глобальный максимум критерия, если F(X) – многоэкстремальная функция. К недостаткам данного метода относится значительное число повторных вычислений F(X), что в случае сложной функции F(X) требует существенных затрат времени.

На практике можно реализовать одну из основных модификаций метода – последовательное уточнение решения, или сканирование с переменным шагом (рис. 16). Рассмотрим иллюстрацию модифицированного метода сканирования: 1 – интервал, включающий в себя искомый максимум функции после первого этапа сканирования (исходный участок разбит на 5 участков); 2 – то же после второго этапа.

На первом этапе сканирование осуществляют с крупным шагом, затем отрезок, внутри которого получено наибольшее значение F(х), Разбивается на более мелкие отрезки, ищется новый отрезок, внутри которого уточненное значение максимума. Он (новый отрезок) опять

Делится на более мелкие и т. д., тех пор, пока величина отрезка, содержащего максимальное значение F(X), не будет меньше заданной погрешности. Главный недостаток этого варианта метода – возможность пропуска «острого» глобального максимума F(X).

Решение. Будем разбивать первоначальный и новый, удовлетворяющий нас, интервал на 4 части, при этом новый шаг рассчитываем по формуле:

Где N – количество частей деления интервала,

Ai, Bi – концы интервала, в котором содержится максимальное значение функции, погрешность , где I — номер итерации.

Видео:Решение биквадратных уравнений. 8 класс.Скачать

Метод прямого сканирования

ВВЕДЕНИЕ

В математике изучение задач на нахождение максимума и минимума началось очень давно. Но только лишь в эпоху формирования математического анализа были созданы первые методы решения и исследования задач на экстремум.

Потребности практической жизни, особенно в области экономики и техники, в последнее время выдвинули такие новые задачи, которые старыми методами решить не удавалось. Надо было идти дальше.

Потребности техники, в частности космической, выдвинули серию задач, которые также не поддавались средствам вариационного исчисления. Необходимость решать их привела к созданию новой теории, получившей название теории оптимального управления. Основной метод в теории оптимально управления был разработан в пятидесятые – шестидесятые годы советскими математиками – Л.С. Понтрягиным и его учениками. Это привело к тому, что теория экстремальных задач получила новый мощный толчок к дальнейшим исследованиям.

В жизни постоянно приходится сталкиваться с необходимостью принять наилучшее возможное (иногда говорят — оптимальное) решение. Огромное число подобных проблем возникает в экономике и технике. При этом часто случается так, что полезно прибегнуть к математике.

В математике исследование задач на максимум и минимум началось очень давно – двадцать пять веков назад, Долгое время к задачам на отыскание экстремумов не было сколько – нибудь единых подходов. Но примерно триста лет назад – в эпоху формирования математического анализа – были созданы первые общие методы решения и исследования задач на экстремум.

Накопление методов дифференциального исчисления приняло наиболее явную форму у Ферма. В 1638 году он сообщил в письме Декарту, что решил задачу определения экстремальных значений функции f(x). Ферма составлял уравнение (f(x+h)-f(x))/h=0 и после преобразований в левой части полагал h=0, вопреки мнению позднейших исследователей, которые видели в этой идеи исчисления бесконечно малых. В действительности, Ферма нашел это условие и аналогичное (f(y)-f(x))/(y-x)=0 при y=x ещё алгебраическими путями.

Рассуждения при нахождении экстремума функции f(x) следующие. Пусть для некоторого x функция достигает максимума. Тогда f(x h)

К сожалению, Ферма не стремился публиковать свои работы, кроме того, пользовался труднодоступными для усвоения алгебраическими средствами Виета с его громоздкой символикой. Видимо, поэтому он не сделал последнего, уже небольшого, шага на пути к созданию дифференциального исчисления.

Накопление фактов дифференциального исчисления происходило быстро. В“Дифференциальном исчислении” (1755) Эйлера это исчисление появляется уже в весьма полном виде.

Правила определения экстремумов функции одной переменной y=f(x) были даны Маклореном. Эйлер разработал этот вопрос для функции двух переменных. Лагранж показал (1789), как отличать вид условного экстремума для функции многих переменных.

ПОСТАНОВКА ЗАДАЧИ

Задача поиска экстремума функции одной переменной возникает при оптимизации целевой функции, зависящей от одной скалярной переменной. Такие задачи входят составной частью во многие итерационные методы решения задач многомерной оптимизации.

Например, численные методы поиска экстремума имеют особенность в том, что их применение не позволяет определить точное значение координат, при котором достигается экстремум функции. В этом случае определяют интервал неопределенности, в котором локализуется экстремум функции.

Величина этого интервала – ∆, определяется исходя из требований точности результата решения при постановке задачи (быстродействие, точность и пр.). Таким образом, численное решение задачи поиска экстремума функции сводится к уменьшению интервала неопределенности от исходного до ∆.

Пусть требуется найти экстремум функции одной переменной Q (u) при отсутствии ограничений на диапазон изменения переменной u.

Необходимым условием существования экстремума непрерывной функции Q (u) является равенство нулю первой производной (dQ / du = 0) или ее отсутствие. Графически равенство нулю производной означает, что касательная к кривой Q (u) в этой точке параллельна оси абсцисс (рис. 1.1, а), на рис. 1.1, б изображен случай, когда производные в точках экстремума не существуют.

Названные условия являются лишь необходимыми условиями. Их выполнение не означает еще, что в данных точках функция имеет экстремум (рис. 1.2).

Для того, чтобы определить, действительно ли в исследуемой точке существует экстремум, необходимо проверить выполнение достаточных условий одним из методов, приведенных ниже:

Рис.1.1 Различные типы экстремума функции одной переменной:
а — производная в точке экстремума существует
б — производная в точке экстремума не существует

Метод сканирования для решения уравнений

Рисунок 1.2 Функции Q(u), удовлетворяющие необходимым условиям экстремума:

а – производная равна нулю;

б – производная не существует;

в – производная равна бесконечности

1Сравнение значений функций.

Этот способ сводится к определению значений функции в точках, расположенных слева и справа в достаточной близости от исследуемой точки, т.е. в точках (u1 – ε), (u1 +ε), где ε – малая положительная величина. Если Q(u1) > Q(u1 – ε) и Q(u1) > Q(u1 + ε), то в точке u1 существует максимум (рис. 1.3). Если Q(u1) Q(u1 – ε) и Q(u1)

Если же знаки производных в точках (u1 – ε) и (u1 + ε) одинаковы, то в точке u1 экстремума нет (рис. 1.3, в).

3Исследование знаков высших производных.

Этот способ применяется в тех случаях, когда исследуемая функция имеет производные высших порядков. Если в точке u1 выполняется необходимое условие экстремума, т.е. и существует вторая производная – , значение которой вычисляется в «подозреваемой» точке u1, то точка u1 является точкой максимума, если , и точкой минимума, если .

Рисунок 1.3 Проверка достаточных условий экстремума:

а – максимум; б – минимум; в – экстремума нет

Если , то для дальнейших исследований вычисляются и т.д.

МЕТОДЫ РЕШЕНИЯ

Метод прямого сканирования

Задача заключается в локализации экстремума функции одной переменной, заданной на интервале [a, b] с точностью до Δ. При решении этой задачи весь интервал разбивается на участки величиной Δ. В узлах разбиения вычисляются значения функции Q и из них выбирается экстремальное. Этот метод требует больших затрат времени (зависящего от значения Δ), но главное его преимущество – это определение глобального экстремума.

Рис. 2.1 Локализация экстремума методом сканирования:

а — геометрическая интерпретация

2.2 Метод половинного деления

Естественным и наиболее распространенным на практике методом поиска экстремума функции одной переменной является метод последовательного деления отрезка пополам. Этот метод был известен еще в древней Греции как метод дихотомии.

Пусть требуется определить экстремум унимодальной функции Q (u) на отрезке [a, b] с точностью Δ. Отрезок [a, b] делится пополам и вычисляются значения функции Q (x1) = F1 и Q (x2) = F2 в точках .

На основе анализа значений F1 и F2 вдвое уменьшается интервал неопределенности и процесс повторяется пока b – a > Δ.

Рисунок 2.2 Метод половинного деления: геометрическая интерпретация

2.3 Метод «золотого сечения»

Гораздо эффективнее, с точки зрения уменьшения затрат на вычисления, метод «золотого сечения»: интервал неопределенности делится не пополам, как в методе дихотомии, а в определенном иррациональном соотношении:

Метод заключается в том, что по заданным a и b как можно точнее определяется значение внутренней точки x1 (см. рис. 2.3, б) по формуле

Точка x2 определяется как точка, симметричная точке x1 на отрезке (a – b). На основе анализа значений F1 = Q (x1) и F2 = Q (x2) интервал неопределенности сокращается путем отбрасывания из рассмотрения отрезка в котором экстремум исключен, исходя из условий унимодальности Q (u). Далее мы определим симметричную точку внутри новых границ, вычисляем значение Q в этой точке, проводим анализ и т.д. до тех пор, пока разность между симметричными точками внутри интервала неопределенности больше Δ.

Рисунок 2.3 Метод «золотого сечения»:

а – золотое сечение; б – геометрическое представление

Метод Фебоначчи

Метод, использующий числа Фибоначчи, позволяет наиболее эффективно достичь заданной точности в поиске экстремума функции Q (u). Числа Фибоначчи определяются соотношением:

При большом «k» отношение соседних чисел Фибоначчи близко к отношению «золотого сечения». Этот метод делит интервал неопределенности не в постоянном соотношении, а в переменном и предполагает некоторое, вполне определенное, зависящее от Δ, число вычислений значений функции Q (u).

По заданному Δ определяется количество вычислений n и соответствующее ему число Фибоначчи F_n , исходя из соотношения:

ПРИМЕР РЕШЕНИЯ

Метод половинного деления

Пусть требуется определить экстремум унимодальной функции Q (u) на отрезке [a, b] с точностью Δ.

Пусть a, b, Δ известны.

· Отрезок [a, b] делится пополам и вычисляются значения функции Q (x1) = F1 и Q (x2) = F2 в точках .

· Если значение a — b > Δ , проверяем отношение F1 Δ.

Блок-схема метода половинного деления представлена на рис.3.1

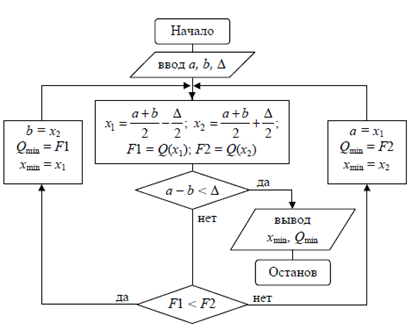Рис. 3.1 — Блок — схема метода половинного деления

3.2 Метод «золотого сечения»

Пусть требуется определить экстремум унимодальной функции Q(u) на отрезке [a, b] с точностью Δ.

Пусть a,b, Δ известны.

1. Рассчитываются начальные точки деления:

;

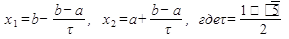
2. Рассчитываются значения целевой функции в этих точках:

;

· Если , то (для поиска max — );

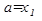
· Иначе ;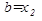

3. Если |b-a| 2 +y 2 +ax+by+c ―>min

a	-8
b
c
d
e
r	-3

1. Записать функцию Лагранжа:

min(x 2 +y 2 -8x+8y+32)

ƒ(x,y)=x 2 +y 2 -8x+8y+32

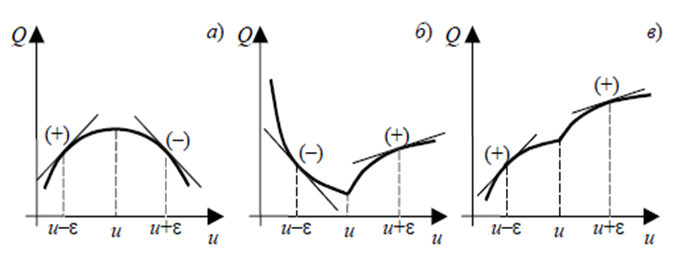
2. Приравнять к нулю градиент функции Лагранжа и найти стационарные точки:

3.Исследовать второй дифференциал функции Лагранжа для каждой стационарной точки на положительность:

ПРИЛОЖЕНИЕ 2

Задание 1.

Рассматривается игра двух лиц, интересы которых противоположны. Такие игры называются антагонистическими играмидвух лиц. В этом случае выигрыш одного игрока равен проигрышу второго.

Предполагается, что каждый игрок может выбрать только одно из конечного множества своих действий. Выбор действия называется выбором стратегии игрока. Если каждый из игроков выбрал свою стратегию, то эта пара стратегий называется ситуацией игры. Каждый игрок знает, какую стратегию выбрал его противник. Чистой стратегией игрока I является выбор одной из n строк матрицы выигрышей А, а чистой стратегией игрока II является выбор одного из столбцов этой же матрицы.

1. Проверяется наличие седловых точек в матрице.

Если седловые точки имеются — выписывается решение игры в чистых стратегиях.

Пусть игрок I выбирает свою стратегию так, чтобы получить максимальный свой выигрыш, а игрок II выбирает свою стратегию так, чтобы минимизировать выигрыш игрока I.

Игроки	B1	B2	B3	B4	B5	a = min(Ai)
A1	-4	-4
A2	-3	-1	-3
A3
A4	-3	-3	-4	-4
A5
b = max(Bi)	―

Находится гарантированный выигрыш, определяемый нижней ценой игры: а=max(a_i)=4, которая указывает на максимальную чистую стратегию А₃.

Верхняя цена игры b=min(b_j)=4.

Седловая точка (3,2) указывает решение на пару альтернатив (А₃, В₂). Цена игры равна 4.

Задание 2.

Игроки	В₁	В₂	В₃	В₄	a = min(Ai)
А1
А2
b = max(Bi )	―

Находится гарантированный выигрыш, определяемый нижней ценой игры a = max(a_i) = 2, которая указывает на максимальную чистую стратегию A₂.
Верхняя цена игры b = min(b_j) = 4.

Это свидетельствует об отсутствии седловой точки, так как a ≠ b, тогда цена игры находится в пределах 2 = 0, p(Cq-α) >= 0; 0 >= p >= 1

(q-1)(Dp-β) >= 0, q(Dp-β) >= 0; 0 >= q >= 1,

C = a11 — a12 — a21 + a22

Проводя необходимые вычисления:

C = 1 — 4 — 5 + 2 = -6

D = -3 — 4 — 8 + 2 = -13

1) p=1,q >= ; p=0, q = ; q=0, p * =min (V_j * ; V_i+C_ij ),

где C_{ij —} расстояние между i и j,

V_i, V_j – значения метки i и j;

46*

∞*

16 i

∞* j

∞*

∞* j

∞*

4. Пункт 2 повторяется до тех пор, пока существуют временные метки.

5. Используя алгоритм «обратного хода», находятся наикратчайшие пути.

46*

∞*

16*

∞*

46*

∞*

46*

∞*

16 i

∞* j

∞*

∞* j

∞*

46*

∞*

41*

∞*

26*

∞*

46*

∞*

41*

∞*

46*

∞*

41*

∞*

26 i

∞*j

∞*

∞*j

∞*

46*

∞*

41*

∞*

46*

∞*

37*

∞*

46*

∞*

41*

∞*

46*

∞*

46*

∞*

41*

∞*

46*

∞*

37j

∞*j

∞*

46*	∞*	∞*	41*	∞*	∞*	46*	∞*	∞*	87*	∞*	∞*
46*	∞*	∞*	∞*	∞*	46*	∞*	∞*	87*	∞*	∞*
46*	∞*	∞*	41i	∞*j	∞*	46*j	∞*	∞*	87*	∞*	∞*

V₁₀ * =min (46*; 41+45 )=min (46*; 86 )=46;

46*	∞*	∞*	72*	∞*	46*	∞*	∞*	87*	∞*	∞*
∞*	∞*	72*	∞*	46*	∞*	∞*	87*	∞*	∞*
46 i	∞*j	∞*	72*	∞*	46*	∞*	∞*	87*	∞*	∞*

86*	∞*	72*	∞*	46*	∞*	∞*	87*	∞*	∞*
86*	∞*	72*	∞*	∞*	∞*	87*	∞*	∞*
86*	∞*	72*	∞*	46 i	∞*j	∞*	87*j	∞*	∞*

V₁₄ * =min (87*; 46+16 )=min (87*; 62 )=62;

86*	∞*	72*	∞*	80*	∞*	62*	∞*	∞*
86*	∞*	72*	∞*	80*	∞*	∞*	∞*
86*	∞*	72*	∞*	80*	∞*	62 i	∞*j	∞*

V₁₅ * =min (∞*; 62+41 )=min (∞*; 103 )=103;

86*	∞*	72 *	∞*	80*	∞*	103*	∞*
86*	∞*	∞*	80*	∞*	103*	∞*
86 *	∞*	72 i	∞*j	80*j	∞*	103*	∞*

V₁₁ * =min (80*; 72+50 )=min (80*; 122)=80;

86 *	∞*	91*	80*	∞*	103*	∞*
86 *	∞*	91*	∞*	103*	∞*
86 *	∞*	91*	80 i	∞*j	103*j	∞*

V₁₂ * =min (108*; 80+28 )=min (108*; 108 )=108;

V₁₅ * =min (103*; 80+28 )=min (103*; 108 )=103;

86*	∞*	91*	108*	103*	∞*
∞*	91*	108*	103*	∞*
86i	∞*j	91*	108*	103*	∞*

93*	91*	108*	103*	∞*
93*	108*	103*	∞*
93*	91 i	108*j	103*	∞*

V₁₂ * =min (108*; 91+47 )=min (108*; 138 )=108;

93*	108*	103*	∞*
108*	103*	∞*
93 i	108*	103*	∞*
108*	103*	∞*
108*	∞*
108*	∞*j

V₁₆ * =min (∞*; 103+39)=min (∞*; 142 )=142;

108*	142*
142*
108 i	142*j

V₁₆ * =min (142*; 108+1)=min (142*; 109)=109;

Кратчайший путь в графе — (1)→(5)→(9)→(10)→(11)→(12)→(16)

2. Остов графа — R’, которое связывает все вершины и имеет минимальную длину: .

(1.2)

(2.6)

(6.5)

(5.9)

(6.7)

(7.8)

(8.4)

(4.3)

(9.10)

(9.13)

(10.11)

(10.14)

(11.15)

(15.16)

(12.16)

;

Видео:11 класс, 27 урок, Общие методы решения уравненийСкачать

Метод сканирования для решения уравнений

1. МЕТОДЫ ОДНОМЕРНОЙ ОПТИМИЗАЦИИ

Метод сканирования в качестве критерия движения к минимуму использует сравнительную оценку величины целевой функции, вычисленной в соответствующих точках.

Интервал поиска ( a , b ) разбивается на несколько равных участков, каждый из которых равен шагу поиска h (рис.1).

Далее последовательно определяются значения функции f ( x ) во всех точках разбиения аргумента и в точках a и b и запоминается наименьшее значение. Таким образом, минимум может быть найден с точностью до h .

Достоинства метода: простота, возможность нахождения глобального минимума.

Недостаток метода: большой объем вычислений, которые необхо димо выполнить при его реализации.

Метод сканирования эффективен при использовании ЭВМ. Блок-схема алгоритма поиска минимума целевой функции R = f ( x ) методом сканирования.