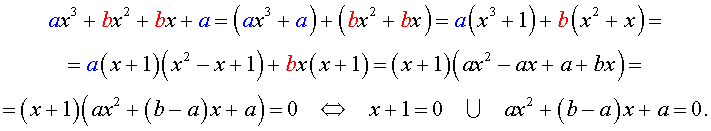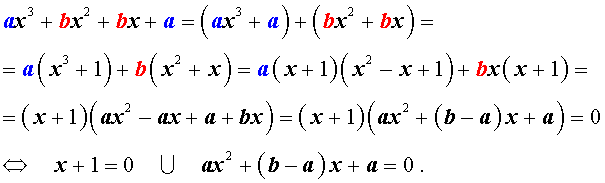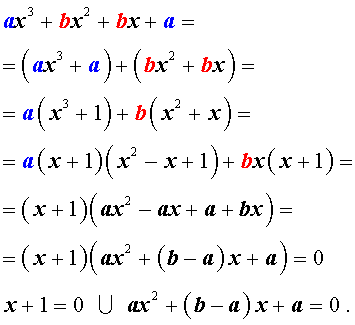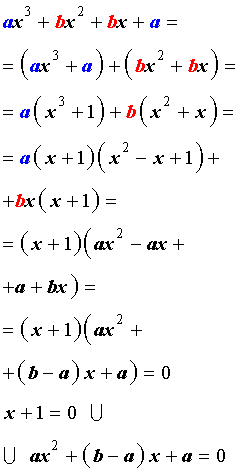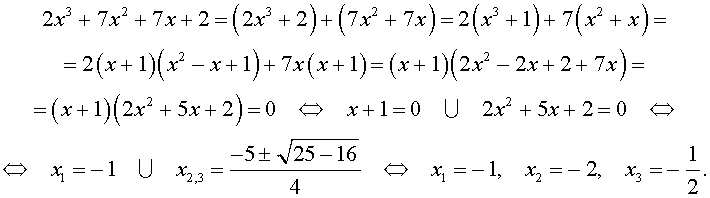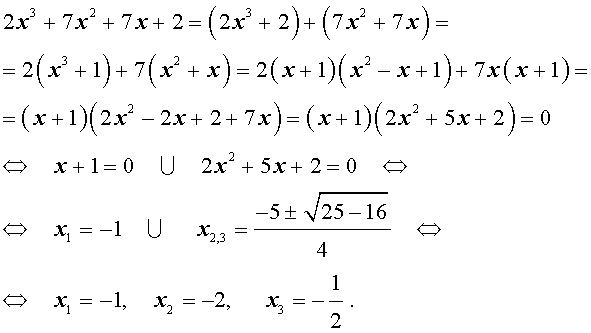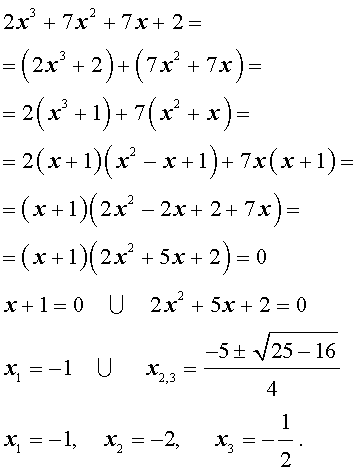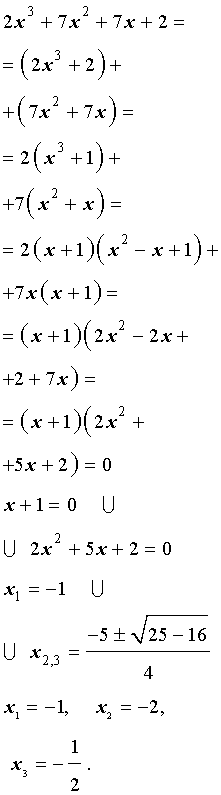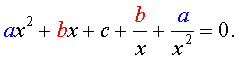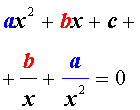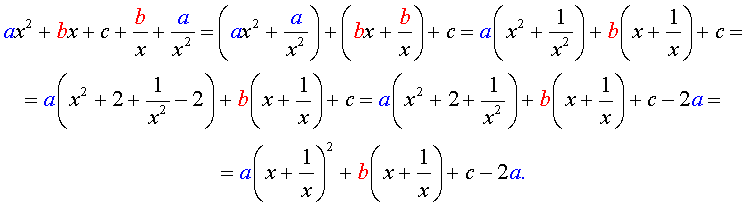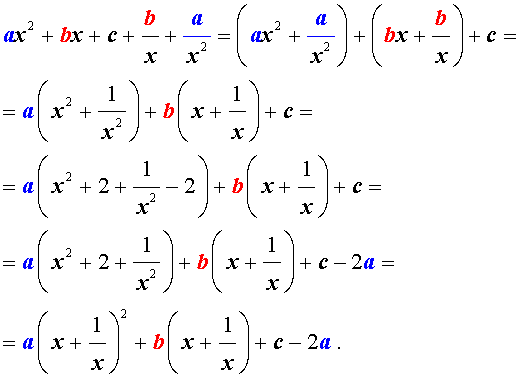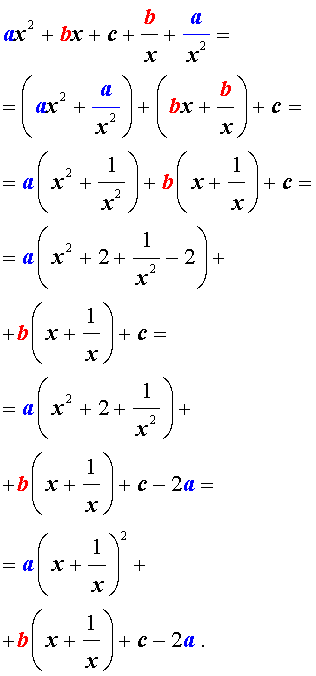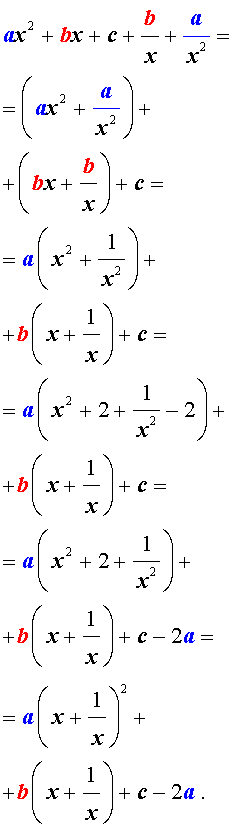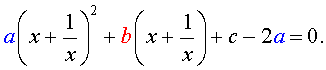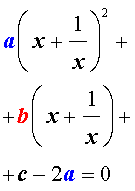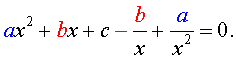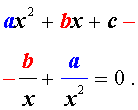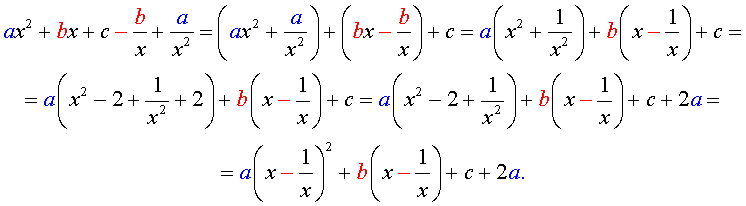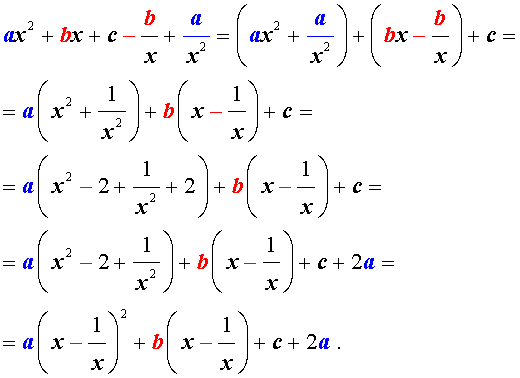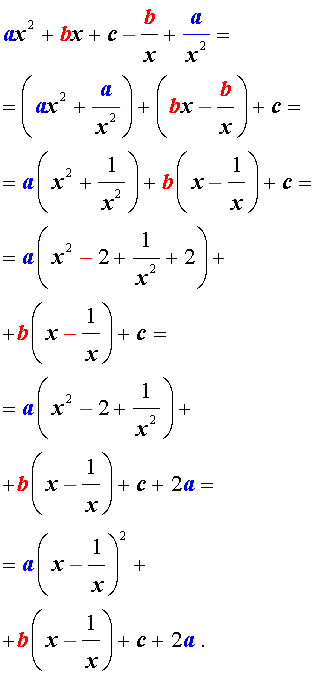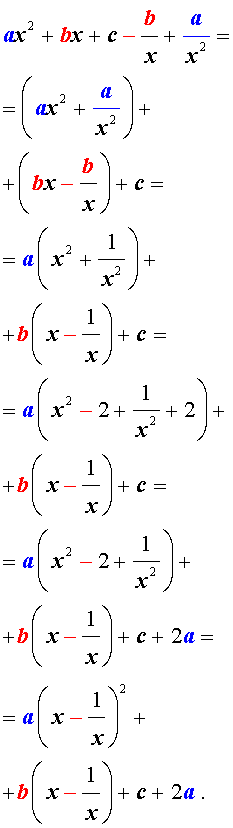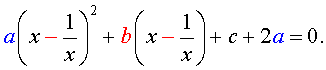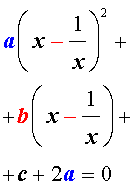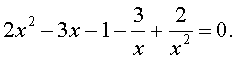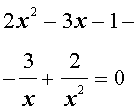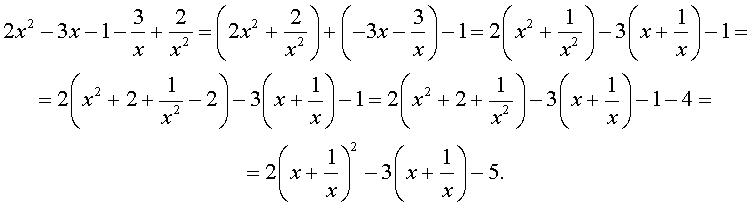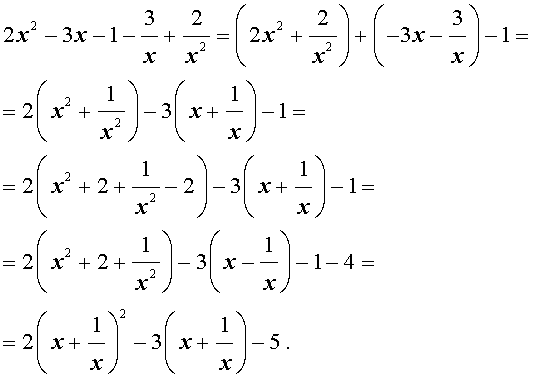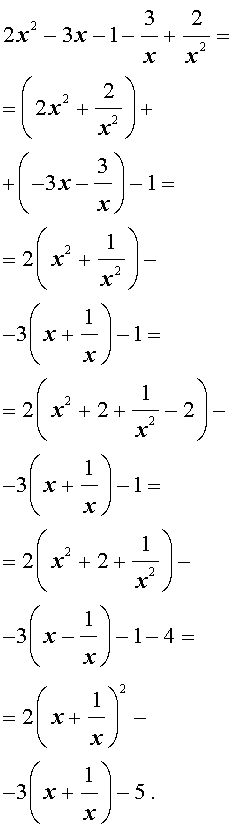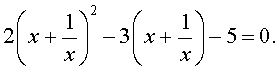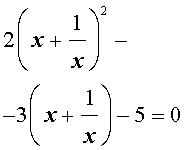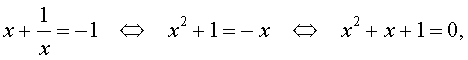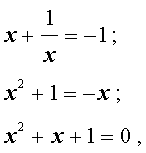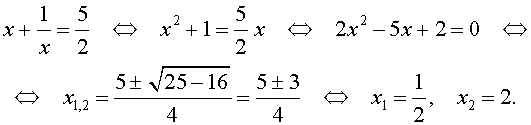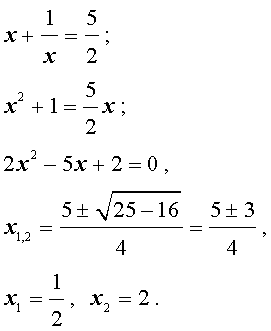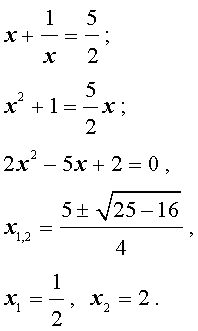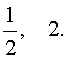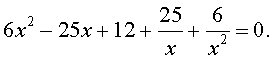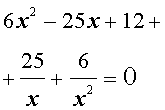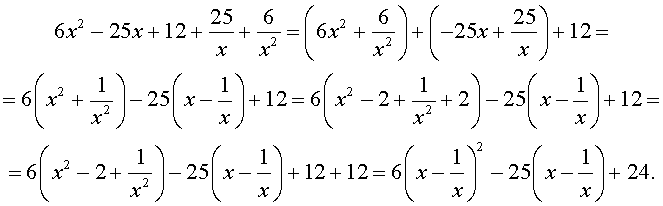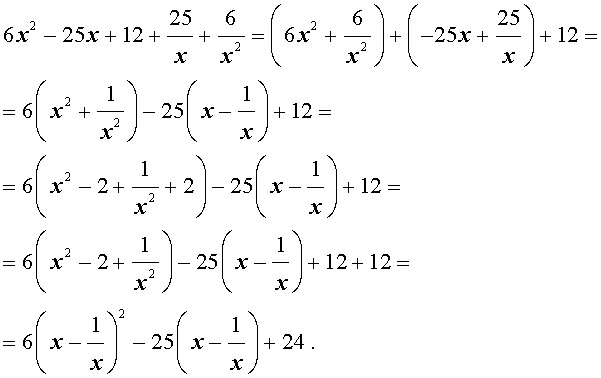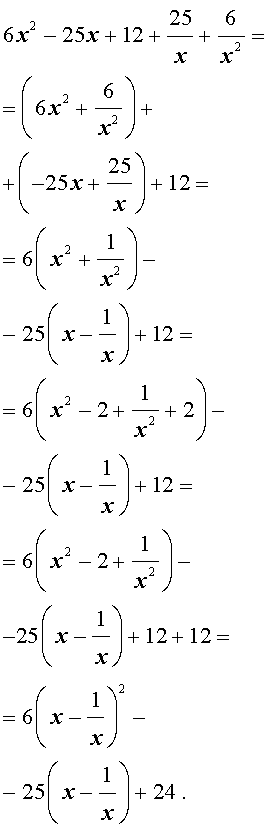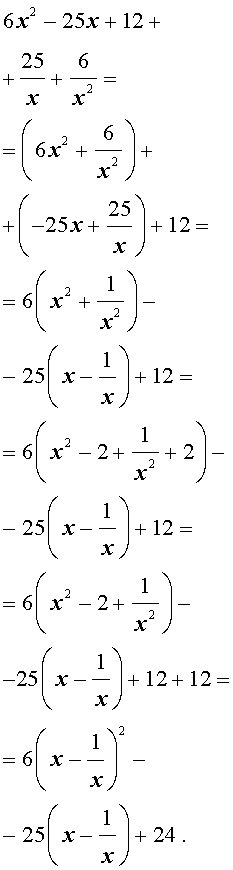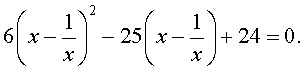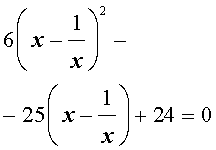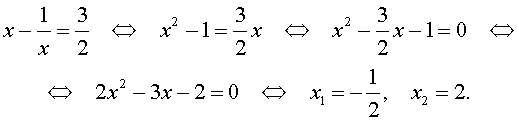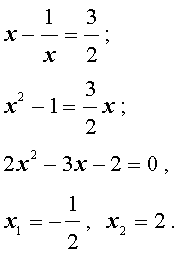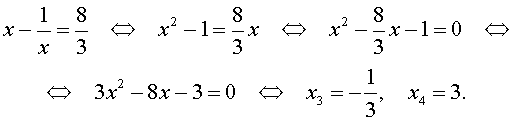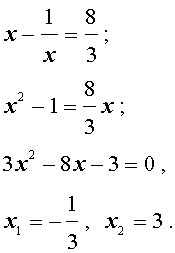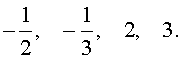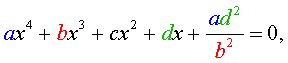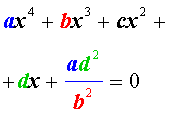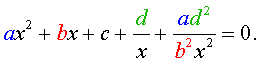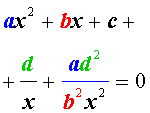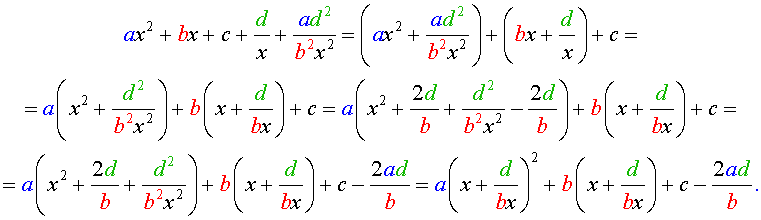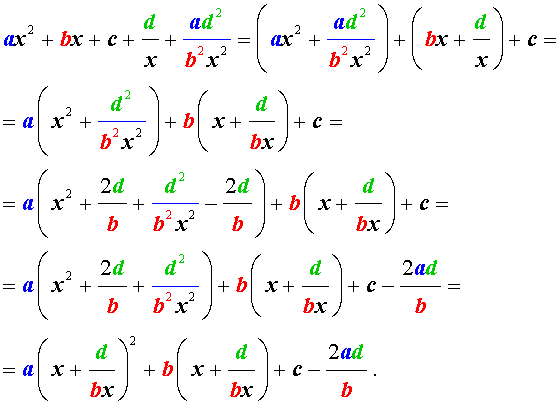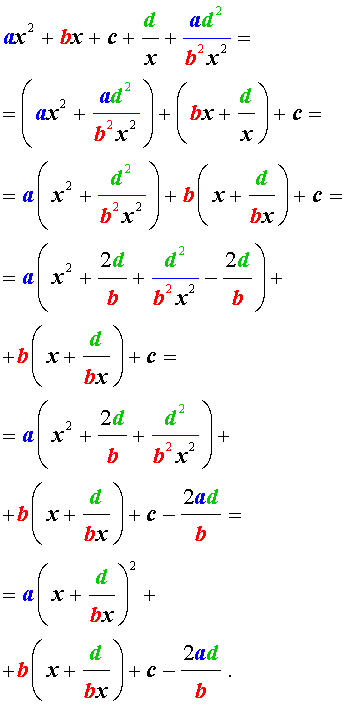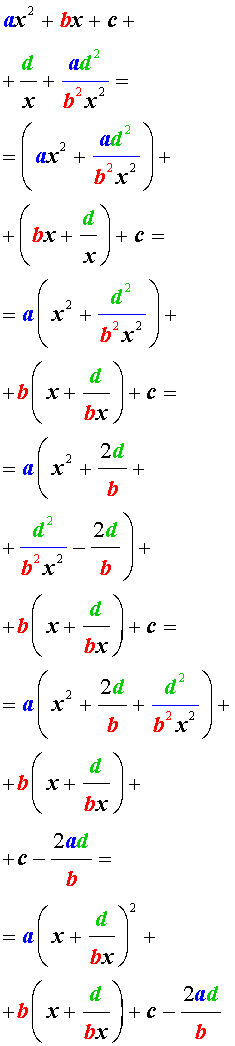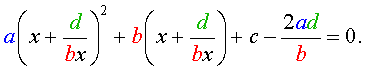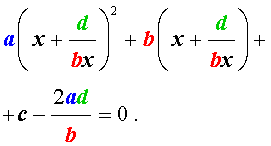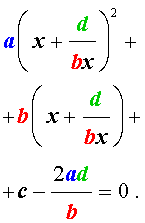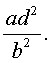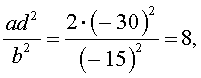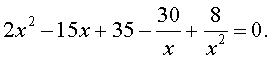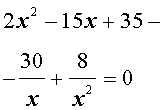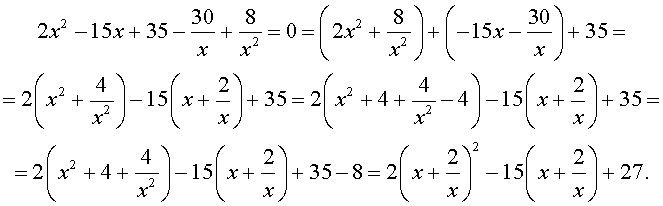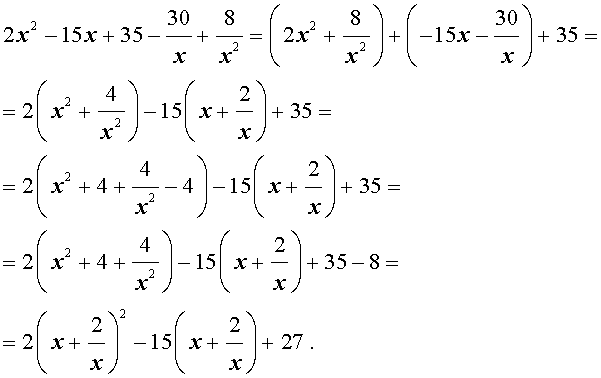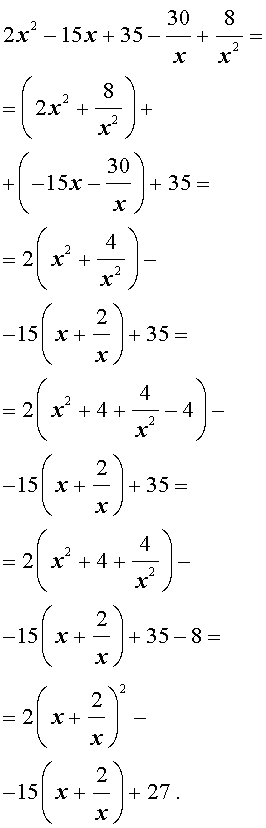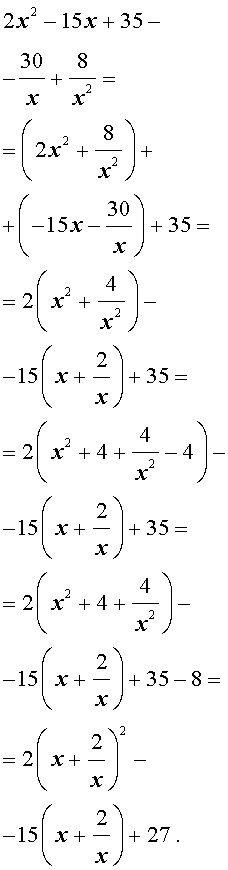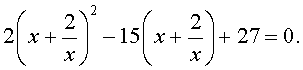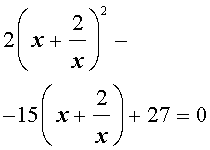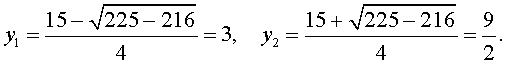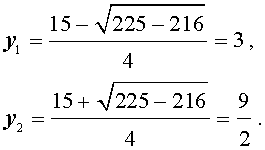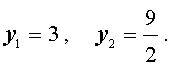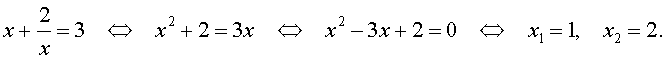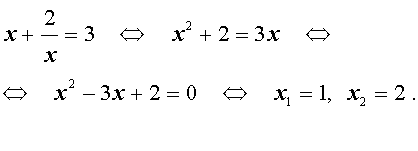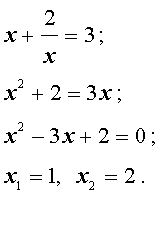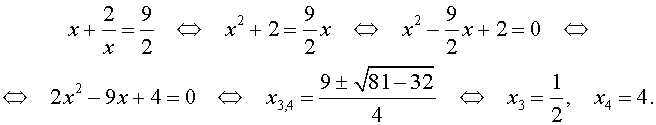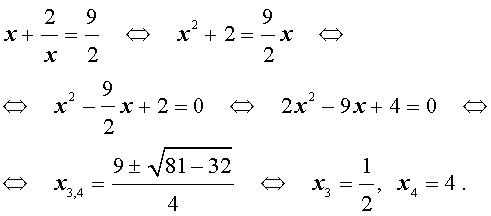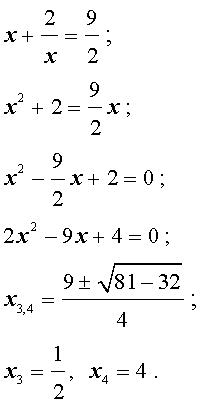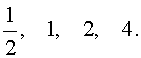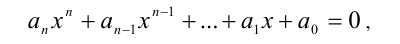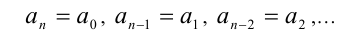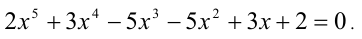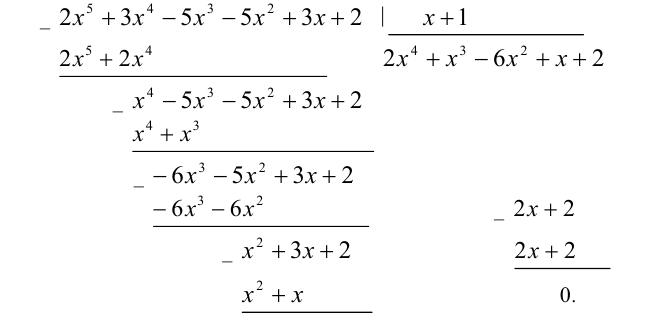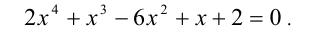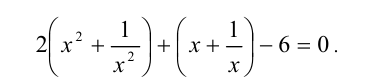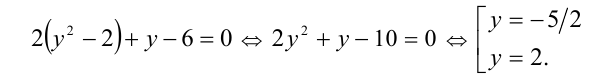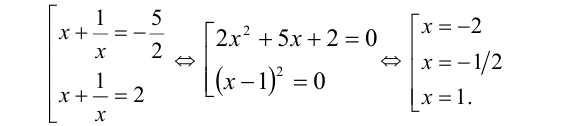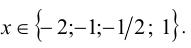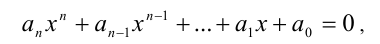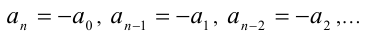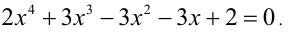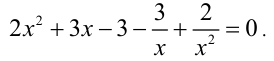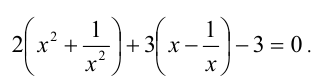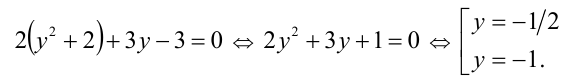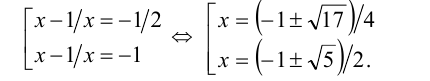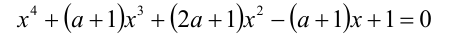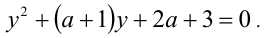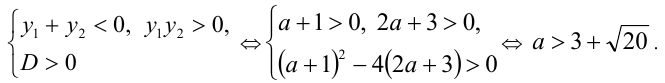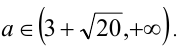возвратные (симметричные) уравнения
Существует ряд уравнений, которые удается решить при помощи сведения их к квадратным уравнениям.
К таким уравнениям, в частности, относятся уравнения следующих типов:
 | Трёхчленные уравнения |
 | Уравнения 4-ой степени, левая часть которых равна произведению четырёх последовательных членов арифметической прогрессии |
 | Возвратные (симметричные) уравнения 3-ей степени |
 | Возвратные (симметричные) уравнения 4-ой степени |
 | Обобщенные возвратные уравнения 4-ой степени |
Замечание . Уравнения, носящие название «Биквадратные уравнения» , относятся к типу «Трехчленные уравнения» .
- Возвратные (симметричные) уравнения 3-ей степени
- Возвратные (симметричные) уравнения 4-ой степени
- Обобщенные возвратные уравнения 4-ой степени
- Метод симметризации при решении уравнений
- Симметрические и кососимметрические уравнения
- Симметрические и кососимметрические уравнения
- Пример №189.
- Пример №190.
- Пример №191.
- 🔍 Видео
Видео:11 класс, 27 урок, Общие методы решения уравненийСкачать

Возвратные (симметричные) уравнения 3-ей степени
Возвратным уравнением 3-ей степени называют уравнение вида
| a x 3 + b x 2 + b x + a = 0, | (1) |
где a , b – заданные числа.
Решение уравнения (1) осуществляется при помощи разложения левой части уравнения (1) на множители:
Для завершения решения уравнения (1) остаётся лишь решить квадратное уравнение
Пример 1 . Решить уравнение
| 2x 3 + 7x 2 + 7x + 2 = 0. | (2) |
Решение . Разложим левую часть уравнения (2) на множители:
Ответ :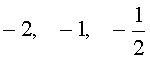
Видео:Решение биквадратных уравнений. 8 класс.Скачать

Возвратные (симметричные) уравнения 4-ой степени
Возвратными (симметричными) уравнениями 4-ой степени называют уравнения вида
| a x 4 + b x 3 + cx 2 + + b x + a = 0, | (3) |
а также уравнения вида
| a x 4 + b x 3 + cx 2 – – b x + a = 0, | (4) |
Для того, чтобы решить возвратное уравнение (3), разделим его на x 2 . В результате получится уравнение
Преобразуем левую часть уравнения (5):
В результате этого преобразования уравнение (5) принимает вид
Если теперь обозначить
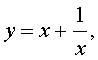 | (7) |
то уравнение (6) станет квадратным уравнением:
| a y 2 + b y + c – 2 a = 0. | (8) |
Найдем корни уравнения (8), а после этого, подставив каждый из найденных корней в равенство (7), решим полученное уравнение относительно x .
Описание метода решения уравнений вида (3) завершено.
Для того, чтобы решить возвратное уравнение (4), разделим его на x 2 . В результате получится уравнение
Преобразуем левую часть уравнения (9):
В результате этого преобразования уравнение (9) принимает вид
Если теперь обозначить
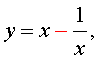 | (11) |
то уравнение (10) станет квадратным уравнением:
| a y 2 + b y + c + 2 a = 0. | (12) |
Найдем корни уравнения (13), а после этого, подставив каждый из найденных корней в равенство (11), решим полученное уравнение относительно x .
Описание метода решения уравнений вида (4) завершено.
Пример 2 . Решить уравнение
| 2x 4 – 3x 3 – x 2 – – 3x + 2 = 0. | (13) |
Решение . Уравнение (13) является возвратным и относится к виду (3). Разделим его на x 2 . В результате получится уравнение
Преобразуем левую часть уравнения (14):
В результате этого преобразования уравнение (14) принимает вид
Если теперь обозначить
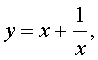 | (16) |
то уравнение (15) станет квадратным уравнением:
| 2y 2 – 3y – 5 = 0. | (17) |
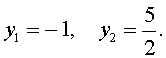 | (18) |
В первом случае из равенства (16) получаем уравнение:
которое решений не имеет.
Во втором случае из равенства (16) получаем:
Ответ :
Пример 3 . Решить уравнение
| 6x 4 – 25x 3 + 12x 2 + + 25x + 6 = 0. | (19) |
Решение . Уравнение (19) является возвратным и относится к виду (4). Разделим его на x 2 . В результате получится уравнение
Преобразуем левую часть уравнения (20):
В результате этого преобразования уравнение (20) принимает вид
Если теперь обозначить
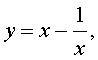 | (22) |
то уравнение (21) станет квадратным уравнением:
| 6y 2 – 25y + 24 = 0. | (23) |
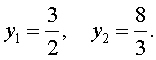 | (24) |
В первом случае из равенства (22) получаем:
Во втором случае из равенства (22) получаем:
Ответ :
Видео:Крутой метод решения уравнений из ЕГЭСкачать

Обобщенные возвратные уравнения 4-ой степени
Обобщенным возвратным уравнением 4-ой степени назовём уравнение вида
где a , b , c, d – заданные числа.
Для того, чтобы решить уравнение (25), разделим его на x 2 . В результате получится уравнение
Преобразуем левую часть уравнения (26):
В результате этого преобразования уравнение (26) принимает вид
Если теперь обозначить
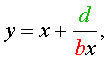 | (28) |
то уравнение (27) станет квадратным уравнением:
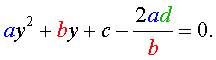 | (29) |
Найдем корни уравнения (29), а после этого, подставив каждый из найденных корней в равенство (28), решим полученное уравнение относительно x .
Описание метода решения уравнений вида (25) завершено.
Пример 4 . Решить уравнение
| 2x 4 – 15x 3 + 35x 2 – – 30 x + 8 = 0. | (30) |
Решение . Введем для коэффициентов уравнения (30) следующие обозначения
и найдем значение выражения
то уравнение (30) является обобщенным возвратным уравнением 4-ой степени. В соответствии с изложенным выше, разделим его на x 2 . В результате получится уравнение
Преобразуем левую часть уравнения (31):
В результате этого преобразования уравнение (31) принимает вид
Если теперь обозначить
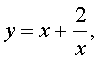 | (33) |
то уравнение (32) станет квадратным уравнением:
| 2y 2 – 15y + 27 = 0. | (34) |
В первом случае из равенства (33) получаем:
Во втором случае из равенства (33) получаем:
Ответ :
Видео:Решение уравнения методом замены переменнойСкачать

Метод симметризации при решении уравнений
Симметрическое уравнение нечетной степени имеет корень x = -1.
Симметрическое уравнение четной степени 2n с помощью подстановки $$ u = x + frac$$ сводится к уравнению степени n
Уравнения вида $$ a_0 x^ + a_1 x^ + . + a_n x^ + a_ x^n + . + a_ x + a_ = 0$$ называют возвратными уравнениями нечетной степени,
если $$frac <<a_>><> = lambda ^ ,quad frac <<a_>><> = lambda ^n ,quad frac <<a_>><> = lambda $$, где $$ lambda$$ — некоторое действительное число.
Возвратное уравнение нечетной степени имеет корень $$ x = — lambda $$.
Возвратное уравнение четной степени 2n с помощью подстановки $$ u = x + frac$$ сводится к уравнению степени n
Если обе части однородного уравнения разделить на $$ left( right)^n$$, применяя замену $$ t = frac<><>$$
получим уравнение $$ a_0 t^n + a_1 t^ + . + a_k t^ + . + a_n = 0$$
Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Симметрические и кососимметрические уравнения
Симметрические и кососимметрические уравнения
Симметрическим уравнением n -й степени называется алгебраическое уравнение вида
где равноотстоящие от концов многочлена коэффициенты равны, т.е.
Рассмотрим отдельно решение симметрических уравнений чётной и нечётной степеней [30].
Если 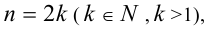
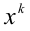
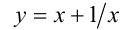
Если же 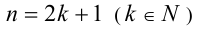
Пример №189.
Решить уравнение
Решение:
Очевидно, имеем симметрическое уравнение 5-й степени. Решаем его по изложенной выше схеме. Одним из корней уравнения будет число x = — 1. Найдём другие корни:
Решим симметрическое уравнение 4-й степени
Поделим для этого обе части уравнения на 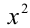
Обозначим у = x + (1/x), тогда
Выполняя обратную подстановку, получаем
Объединяя полученные решения, приходим к ответу:
Кососимметрическим уравнением n -й степени называется уравнение вида
где равноотстоящие от концов многочлена коэффициенты являются противоположными числами, т.е.
Решение кососимметрических уравнений чётной и нечётной степени во многом аналогично решению соответствующих симметрических уравнений.
Если 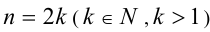
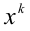
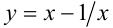
Если же 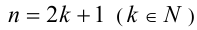
Пример №190.
Решить уравнение
Решение:
Это кососимметрическое уравнение 4-й степени. Поскольку x = 0 не является корнем уравнения, то поделим обе его части на 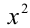
Перепишем последнее уравнение в виде
Положим у = х — (1/x), тогда получим
Выполняя обратную подстановку, получаем 4 решения
Пример №191.
Найти все значения параметра а , при которых уравнение
на промежутке 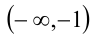
Решение:
Так как 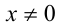
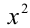
Поскольку функция у =x — (1/x) возрастает на промежутке 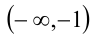
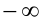
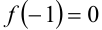
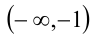
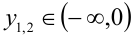
Ответ:
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
🔍 Видео
Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

УРАВНЕНИЯ С МОДУЛЕМ. Метод интервалов для решения уравнений.Скачать

СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать

Решение квадратных уравнений. Метод разложения на множители. 8 класс.Скачать

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

СИСТЕМЫ УРАВНЕНИЙ В ЕГЭ ЧАСТЬ I #shorts #математика #егэ #огэ #профильныйегэСкачать

9 класс, 11 урок, Методы решения систем уравненийСкачать

Метод оценки при решении уравненийСкачать

Методы решения уравненийСкачать

Как решают уравнения в России и США!?Скачать

Повторяем решение уравнений. Полезно всем! Вебинар | МатематикаСкачать

Ошибка при решении уравненияСкачать

Матричный метод решения систем уравненийСкачать

Метод решения уравнений, чтобы не ошибаться в знакахСкачать

Решение матричных уравненийСкачать