Метод секущих и касательных для решения нелинейных уравнений

Задачи решения уравнений постоянно возникают на практике, например, в экономике, развивая бизнес, вы хотите узнать, когда прибыль достигнет определенного значения, в медицине при исследовании действия лекарственных препаратов, важно знать, когда концентрация вещества достигнет заданного уровня и т.д.

В задачах оптимизации часто необходимо определять точки, в которых производная функции обращается в 0, что является необходимым условием локального экстремума.

В статистике при построении оценок методом наименьших квадратов или методом максимального правдоподобия также приходится решать нелинейные уравнения и системы уравнений.

Итак, возникает целый класс задач, связанных с нахождением решений нелинейных уравнений, например, уравнения или уравнения и т.д.

В простейшем случае у нас имеется функция , заданная на отрезке ( a , b ) и принимающая определенные значения.

Каждому значению x из этого отрезка мы можем сопоставить число , это и есть функциональная зависимость, ключевое понятие математики.

Нам нужно найти такое значение при котором такие называются корнями функции

Визуально нам нужно определить точку пересечения графика функции с осью абсцисс.

Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать

Метод деления пополам

Простейшим методом нахождения корней уравнения является метод деления пополам или дихотомия.

Этот метод является интуитивно ясным и каждый действовал бы при решении задачи подобным образом.

Алгоритм состоит в следующем.

Предположим, мы нашли две точки и , такие что и имеют разные знаки, тогда между этими точками находится хотя бы один корень функции .

Поделим отрезок пополам и введем среднюю точку .

Тогда либо , либо .

Оставим ту половину отрезка, для которой значения на концах имеют разные знаки. Теперь этот отрезок снова делим пополам и оставляем ту его часть, на границах которой функция имеет разные знаки, и так далее, достижения требуемой точности.

Очевидно, постепенно мы сузим область, где находится корень функции, а, следовательно, с определенной степенью точности определим его.

Заметьте, описанный алгоритм применим для любой непрерывной функции.

К достоинствам метода деления пополам следует отнести его высокую надежность и простоту.

Недостатком метода является тот факт, что прежде чем начать его применение, необходимо найти две точки, значения функции в которых имеют разные знаки. Очевидно, что метод неприменим для корней четной кратности и также не может быть обобщен на случай комплексных корней и на системы уравнений.

Порядок сходимости метода линейный, на каждом шаге точность возрастает вдвое, чем больше сделано итераций, тем точнее определен корень.

Видео:Метод секущихСкачать

Метод Ньютона: теоретические основы

Классический метод Ньютона или касательных заключается в том, что если — некоторое приближение к корню уравнения , то следующее приближение определяется как корень касательной к функции , проведенной в точке .

Уравнение касательной к функции в точке имеет вид:

В уравнении касательной положим и .

Тогда алгоритм последовательных вычислений в методе Ньютона состоит в следующем:

Сходимость метода касательных квадратичная, порядок сходимости равен 2.

Таким образом, сходимость метода касательных Ньютона очень быстрая.

Запомните этот замечательный факт!

Без всяких изменений метод обобщается на комплексный случай.

Если корень является корнем второй кратности и выше, то порядок сходимости падает и становится линейным.

Упражнение 1. Найти с помощью метода касательных решение уравнения на отрезке (0, 2).

Упражнение 2. Найти с помощью метода касательных решение уравнения на отрезке (1, 3).

К недостаткам метода Ньютона следует отнести его локальность, поскольку он гарантированно сходится при произвольном стартовом приближении только, если везде выполнено условие , в противной ситуации сходимость есть лишь в некоторой окрестности корня.

Недостатком метода Ньютона является необходимость вычисления производных на каждом шаге.

Видео:Численное решение уравнений, урок 4/5. Метод касательных (Ньютона)Скачать

Визуализация метода Ньютона

Метод Ньютона (метод касательных) применяется в том случае, если уравнение f(x) = 0 имеет корень , и выполняются условия:

1) функция y= f(x) определена и непрерывна при ;

2) f(a)·f(b) 0. Таким образом, выбирается точка с абсциссой x₀, в которой касательная к кривой y=f(x) на отрезке [a;b] пересекает ось Ox. За точку x₀ сначала удобно выбирать один из концов отрезка.

Рассмотрим метод Ньютона на конкретном примере.

Пусть нам дана возрастающая функция y = f(x) =x 2 -2, непрерывная на отрезке (0;2), и имеющая f ‘(x) = 2x > 0 и f »(x) = 2 > 0.

Уравнение касательной в общем виде имеет представление:

В нашем случае: y-y₀=2x₀·(x-x₀). В качестве точки x₀ выбираем точку B₁(b; f(b)) = (2,2). Проводим касательную к функции y = f(x) в точке B₁, и обозначаем точку пересечения касательной и оси Ox точкой x₁. Получаем уравнение первой касательной:y-2=2·2(x-2), y=4x-6.

Точка пересечения касательной и оси Ox: x₁ =

Рисунок 2. Результат первой итерации

Затем находим точку пересечения функции y=f(x) и перпендикуляра, проведенного к оси Ox через точку x₁, получаем точку В₂ =(1.5; 0.25). Снова проводим касательную к функции y = f(x) в точке В₂, и обозначаем точку пересечения касательной и оси Ox точкой x₂.

Точка пересечения касательной и оси Ox: x₂ = .

Рисунок 3. Вторая итерация метода Ньютона

Затем находим точку пересечения функции y=f(x) и перпендикуляра, проведенного к оси Ox через точку x₂, получаем точку В₃ и так далее.

В3 = ()

Рисунок 4. Третий шаг метода касательных

Первое приближение корня определяется по формуле:

= 1.5.

Второе приближение корня определяется по формуле:

=

Третье приближение корня определяется по формуле:

Таким образом, i-ое приближение корня определяется по формуле:

Вычисления ведутся до тех пор, пока не будет достигнуто совпадение десятичных знаков, которые необходимы в ответе, или заданной точности e — до выполнения неравенства |xi—xi-1|

using namespace std;

float f(double x) //возвращает значение функции f(x) = x^2-2

float df(float x) //возвращает значение производной

float d2f(float x) // значение второй производной

int _tmain(int argc, _TCHAR* argv[])

int exit = 0, i=0;//переменные для выхода и цикла

double x0,xn;// вычисляемые приближения для корня

double a, b, eps;// границы отрезка и необходимая точность

cin>>a>>b; // вводим границы отрезка, на котором будем искать корень

cin>>eps; // вводим нужную точность вычислений

if (a > b) // если пользователь перепутал границы отрезка, меняем их местами

if (f(a)*f(b)>0) // если знаки функции на краях отрезка одинаковые, то здесь нет корня

cout 0) x0 = a; // для выбора начальной точки проверяем f(x0)*d2f(x0)>0 ?

xn = x0-f(x0)/df(x0); // считаем первое приближение

cout eps) // пока не достигнем необходимой точности, будет продолжать вычислять

xn = x0-f(x0)/df(x0); // непосредственно формула Ньютона

> while (exit!=1); // пока пользователь не ввел exit = 1

Посмотрим, как это работает. Нажмем на зеленый треугольник в верхнем левом углу экрана, или же клавишу F5.

Если происходит ошибка компиляции «Ошибка error LNK1123: сбой при преобразовании в COFF: файл недопустим или поврежден», то это лечится либо установкой первого Service pack 1, либо в настройках проекта Свойства -> Компоновщик отключаем инкрементную компоновку.

Рис. 4. Решение ошибки компиляции проекта

Мы будем искать корни у функции f(x) = x2-2.

Сначала проверим работу приложения на «неправильных» входных данных. На отрезке [3; 5] нет корней, наша программа должна выдать сообщение об ошибке.

У нас появилось окно приложения:

Рис. 5. Ввод входных данных

Введем границы отрезка 3 и 5, и точность 0.05. Программа, как и надо, выдала сообщение об ошибке, что на данном отрезке корней нет.

Рис. 6. Ошибка «На этом отрезке корней нет!»

Выходить мы пока не собираемся, так что на сообщение «Exit?» вводим «0».

Теперь проверим работу приложения на корректных входных данных. Введем отрезок [0; 2] и точность 0.0001.

Рис. 7. Вычисление корня с необходимой точностью

Как мы видим, необходимая точность была достигнута уже на 4-ой итерации.

Чтобы выйти из приложения, введем «Exit?» => 1.

Видео:Численное решение уравнений, урок 3/5. Метод хордСкачать

Метод секущих

Чтобы избежать вычисления производной, метод Ньютона можно упростить, заменив производную на приближенное значение, вычисленное по двум предыдущим точкам:

/

Итерационный процесс имеет вид:

где .

Это двухшаговый итерационный процесс, поскольку использует для нахождения последующего приближения два предыдущих.

Порядок сходимости метода секущих ниже, чем у метода касательных и равен в случае однократного корня .

Эта замечательная величина называется золотым сечением:

Убедимся в этом, считая для удобства, что .

Таким образом, с точностью до бесконечно малых более высокого порядка

Отбрасывая остаточный член, получаем рекуррентное соотношение, решение которого естественно искать в виде .

После подстановки имеем: и

Для сходимости необходимо, чтобы было положительным, поэтому .

Поскольку знание производной не требуется, то при том же объёме вычислений в методе секущих (несмотря на меньший порядок сходимости) можно добиться большей точности, чем в методе касательных.

Отметим, что вблизи корня приходится делить на малое число, и это приводит к потере точности (особенно в случае кратных корней), поэтому, выбрав относительно малое , выполняют вычисления до выполнения и продолжают их пока модуль разности соседних приближений убывает.

Как только начнется рост, вычисления прекращают и последнюю итерацию не используют.

Такая процедура определения момента окончания итераций называется приемом Гарвика.

Видео:15 Метод Ньютона (Метод касательных) Ручной счет Численные методы решения нелинейного уравненияСкачать

Метод парабол

Рассмотрим трехшаговый метод, в котором приближение определяется по трем предыдущим точкам , и .

Для этого заменим, аналогично методу секущих, функцию интерполяционной параболой проходящей через точки , и .

В форме Ньютона она имеет вид:

Точка определяется как тот из корней этого полинома, который ближе по модулю к точке .

Порядок сходимости метода парабол выше, чем у метода секущих, но ниже, чем у метода Ньютона.

Важным отличием от ранее рассмотренных методов, является то обстоятельство, что даже если вещественна при вещественных и стартовые приближения выбраны вещественными, метод парабол может привести к комплексному корню исходной задачи.

Этот метод очень удобен для поиска корней многочленов высокой степени.

Видео:Метод касательных (метод Ньютона)Скачать

Метод простых итераций

Задачу нахождения решений уравнений можно формулировать как задачу нахождения корней: , или как задачу нахождения неподвижной точки.

Пусть и — сжатие: (в частности, тот факт, что — сжатие, как легко видеть, означает, что).

По теореме Банаха существует и единственна неподвижная точка

Она может быть найдена как предел простой итерационной процедуры

где начальное приближение — произвольная точка промежутка .

Если функция дифференцируема, то удобным критерием сжатия является число . Действительно, по теореме Лагранжа

Таким образом, если производная меньше единицы, то является сжатием.

Условие существенно, ибо если, например, на [0,1] , то неподвижная точка отсутствует, хотя производная равна нулю. Скорость сходимости зависит от величины . Чем меньше , тем быстрее сходимость.

Рассмотрим уравнение: .

Если в качестве взять функцию , то соответствующая итерационная процедура будет иметь вид: . Как нетрудно убедиться, метод итераций в данном случае расходится при любой начальной точке , не совпадающей с собственно неподвижной точкой .

Однако можно в качестве можно взять, например, функцию . Соответствующая итерационная процедура имеет вид: .

Эти итерации сходятся к неподвижной точке для любого начального приближения :

Действительно, в первом случае , т.е. для выполнения условия необходимо чтобы , но тогда . Таким образом, отображение сжатием не является.

Рассмотрим , неподвижная точка та же самая, ситуация другая. Здесь, хотя формально производная может быть довольно большой (при малых ж), однако уже на следующем шаге она будет меньше 1.

т.е. такой итерационный процесс всегда сходится.

Метод Ньютона представляет собой частный случай метода простых итераций.

Здесь нетрудно убедиться, что при существует окрестность корня, в которой .

то если корень кратности , то в его окрестности и, следовательно,.

Если — простой корень, то сходимость метода касательных квадратичная (то есть порядок сходимости равен 2).

Поскольку , то

Таким образом, сходимость метода Ньютона очень быстрая.

Видео:Методы численного анализа - Метод Ньютона, секущих для решения систем нелинейных уравненийСкачать

Нахождение всех корней уравнения

Недостатком почти всех итерационных методов нахождения корней является то, что они при однократном применении позволяют найти лишь один корень функции, к тому же, мы не знаем какой именно.

Чтобы найти другие корни, можно было бы брать новые стартовые точки и применять метод вновь, но нет гарантии, что при этом итерации сойдутся к новому корню, а не к уже найденному, если вообще сойдутся.

Для поиска других корней используется метод удаления корней.

Пусть — корень функции , рассмотрим функцию. Точка будет являться корнем функции на единицу меньшей кратности, чем, при этом все остальные корни у функций и совпадают с учетом кратности.

Применяя тот или иной метод нахождения корней к функции , мы найдем новый корень (который может в случае кратных корней и совпадать с ). Далее можно рассмотреть функцию и искать корни у неё.

Повторяя указанную процедуру, можно найти все корни с учетом кратности.

Заметим, что когда мы производим деление на тот или иной корень , то в действительности мы делим лишь на найденное приближение , и, тем самым, несколько сдвигаем корни вспомогательной функции относительно истинных корней функции . Это может привести к значительным погрешностям, если процедура отделения применялась уже достаточное число раз.

Чтобы избежать этого, с помощью вспомогательных функций вычисляются лишь первые итерации, а окончательные проводятся по исходной функции , используя в качестве стартового приближения, последнюю итерацию, полученную по вспомогательной функции.

Мы рассмотрели решение уравнений только в одномерном случае, нахождение решений многомерных уравнений существенно более трудная задача.

Видео:Метод простых итераций пример решения нелинейных уравненийСкачать

Схожесть и различие метода касательных и секущих решения нелинейных уравнений

В методе Ньютона необходимо вычислять производные . Это может потребовать много времени, может оказаться трудным или даже невозможным делом, особенно если вычисление включает, например, вычисление интеграла, решение дифференциального уравнения или если значение функции определяется результатом работы некоторого физического устройства.

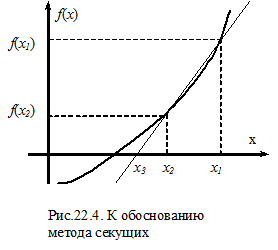Значение производной можно вычислить приблизительно по значениям функции в двух точках x₁ и x₂, как это показано на рис.22.4.

Заменив в формуле (22.1.) производную ее приближенным значением

,

По сравнению с методом Ньютона из-за погрешности в определении производной для нахождения корня требуется выполнить большее количество шагов. Однако в методе секущих на каждом шаге вычисляется только одно значение функции, в то время как в методе Ньютона вычисляются значения функции и ее производной, поэтому скорость счета у них приблизительно одинакова. Недостаток метода секущих связан с тем, что в знаменателе формулы (22.2) стоит разность значений функции. Вдали от корня это несущественно, но вблизи от корня значения функции малы и очень близки. В результате этого возникает потеря значащих цифр, приводящая к «разболтке» счета, когда результаты вычисления начинают колебаться около истинного значения, не сходясь к нему. Это ограничивает точность счета.

Следует отметить еще одну сторону метода секущих. Формула (22.2) идентична формуле метода хорд:

.

Однако, метод касательных не требует указания диапазона изменения знака функции и при этом обеспечивает обычно большую скорость расчета, чем метод хорд. В свою очередь, метод хорд гарантирует нахождения корня и исключает возможность появления «разболтки», так как корень всегда находится внутри диапазона неопределенности и длина диапазона сокращается на каждом шаге.

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.006 сек.)

Видео:Решение нелинейного уравнения методом хорд (секущих) (программа)Скачать

Метод секущих и касательных для решения нелинейных уравнений

Pers.narod.ru. Обучение. Лекции по численным методам. Приближённое решение нелинейных алгебраических уравнений

1. Приближенное решение нелинейных алгебраических уравнений

Дано нелинейное алгебраическое уравнение

Нелинейность уравнения означает, что график функции не есть прямая линия, т.е. в f(x) входит x в некоторой степени или под знаком функции.

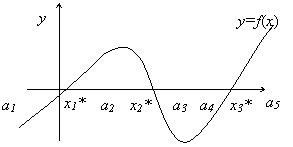
Решить уравнение – это найти такое x* ∈ R: f(x*)=0. Значение x* называют корнем уравнения. Нелинейное уравнение может иметь несколько корней. Геометрическая интерпретация корней уравнения представлена на рис. 1. Корнями уравнения (1) являются точки x₁*, x₂*, x₃*, в которых функция f(x) пересекает ось x.

Методы решения нелинейного уравнения (1) можно разделить на точные (аналитические) и приближенные (итерационные). В точных методах корень представляется некоторой алгебраической формулой. Например, решение квадратных уравнений, некоторых тригонометрических уравнений и т. д.

В приближенных методах процесс нахождения решения, вообще говоря, бесконечен. Решение получается в виде бесконечной последовательности <x_n>, такой, что 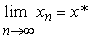. По определению предела, для любого (сколь угодно малого) ε, найдется такое N, что при n>N, |x_n – x*| / (x) не меняет знак на отрезке [a, b], т.е. f(x) – монотонная функция, в этом случае отрезок [a,b] будет интервалом изоляции.

Если корней несколько, то для каждого нужно найти интервал изоляции.

Существуют различные способы исследования функции: аналитический, табличный, графический.

Аналитический способ состоит в нахождении экстремумов функции f(x), исследование ее поведения при 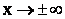и нахождение участков возрастания и убывания функции.

Графический способ – это построение графика функции f(x) и определение числа корней по количеству пересечений графика с осью x.

Табличный способ – это построение таблицы, состоящей из столбца аргумента x и столбца значений функции f(x). О наличии корней свидетельствуют перемены знака функции. Чтобы не произошла потеря корней, шаг изменения аргумента должен быть достаточно мелким, а интервал изменения достаточно широким.

Решить уравнение x 3 ‑ 6x 2 +3x+11=0, т.е. f(x)= x 3 ‑ 6x 2 +3x+11.

Найдем производную f / (x)=3x 2 -12x+3.

Найдем нули производной f / (x)=3x 2 -12x+3=0; D=144-4*3*3=108;

X₁=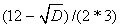= 0.268;

X₂=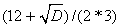= 3.732;

Так как f / ()>0, то f / (x)>0 при , f / (x) / (x)>0 при . Кроме того, f()= 0. Следовательно, на интервале возрастает от до f(x₁)= 3x₁ 2 -12x₁+3=11.39; на интервале — убывает до f(x₂)= 3x₂ 2 -12x₂+3=-9.39 и на интервале возрастает до , т.е. уравнение имеет три корня.

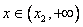
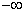
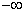
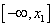
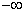
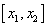
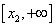
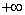
Найдем интервалы изоляции для каждого из корней.

Рассмотрим для первого корня отрезок [-2, -1]:

f(-2)= -27 0, f / (x)>0 при 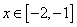т.е. этот отрезок является интервалом изоляции корня.

Рассмотрим для второго корня отрезок [1, 3]:

f(1)= 9>0, f(3)= -7 / (x) 0, f / (x)>0 при 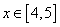т.е. этот отрезок является интервалом изоляции корня.

📸 Видео

Метод Ньютона | Лучший момент из фильма Двадцать одно 21Скачать

Метод Хорд - ВизуализацияСкачать

Метод половинного деления решение нелинейного уравненияСкачать

Решение нелинейного уравнения методом Ньютона (касательных) (программа)Скачать

Метод хордСкачать

Алгоритмы С#. Метод секущих(хорд)Скачать

Метод Ньютона (Метод касательных)Скачать

Численный метод Ньютона в ExcelСкачать

Численное решение уравнений, урок 5/5. Комбинированный метод хорд и касательныхСкачать

11 Метод Ньютона (Метод касательных) Mathcad Численные методы решения нелинейного уравненияСкачать

МЗЭ 2021 Лекция 11 Метод Ньютона для решения систем нелинейных уравненийСкачать