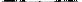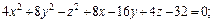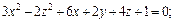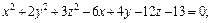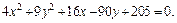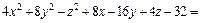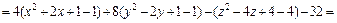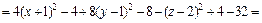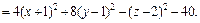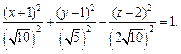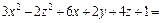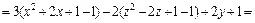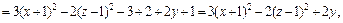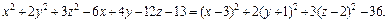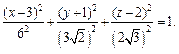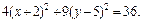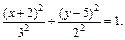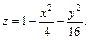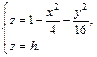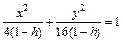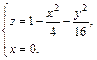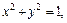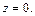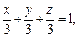§21. Поверхности второго порядка. Исследование методом сечений.
Общий вид алгебраической поверхности второго порядка представляет собой многочлен второй степени относительно трех переменных:
Одним из наиболее продуктивных методов изучения поверхностей в пространстве является метод сечений. Он заключается в исследовании кривых, получающихся в сечениях поверхности плоскостями, параллельными координатным. Для этого достаточно зафиксировать одну из переменных в уравнении поверхности и получить, тем самым, уравнение кривой в плоскости, параллельной двум другим координатным осям. Этот метод будет использован в последующих параграфах при исследовании поверхностей второго порядка. При этом будут рассматриваться только уравнения, непосредственно сводящиеся к каноническим.
Видео:Аналитическая геометрия, 8 урок, Поверхности второго порядкаСкачать

Метод сечений в исследовании уравнений поверхностей
8.4. Построение поверхностей
Мы приступаем к изучению формы поверхностей второго порядка, определённых в предыдущем разделе своими каноническими уравнениями. Напомним, что это вторая из двух основных задач аналитической геометрии: зная уравнение поверхности, изучить её геометрические свойства.
Метод, который мы будем применять, называется методом сечений: пересекая поверхность плоскостями, параллельными координатным плоскостям, будем рассматривать линии пересечения и по их виду делать выводы о форме поверхности.
Каноническое уравнение эллипсоида:
Отметим симметрию поверхности: если точка (x, у, z) лежит на эллипсоиде, то и все точки (±x, ±у, ±z) тоже лежат на эллипсоиде. Значит, поверхность симметрична относительно любой из координатных плоскостей. Пересечём эллипсоид плоскостью z = h. Получим линию
Это эллипс, полуоси которого убывают с увеличением |h|. При h = c эллипс превращается в точку, при h > c плоскость z = h не пересекает эллипсоид. Эллипсы получаются и при сечении эллипсоида плоскостями x = h, у = h. Используя эти данные, изображаем поверхность. Числа a, b, c называются полуосями эллипсоида. Если две полуоси равны, то получается эллипсоид вращения. Например, эллипсоид, образованный при вращении эллипса (лежит в плоскости XOZ) вокруг оси OZ. Если a = b = c, то эллипсоид превращается в сферу.
Видео:Поверхности второго порядкаСкачать

Поверхности второго порядка
Поверхностью второго порядка называется поверхность S, общее уравнение которой в декартовой прямоугольной системе координат имеет вид:
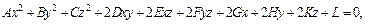
где коэффициенты при одночленах второй степени одновременно не равны нулю.
Существует девять типов невырожденных поверхностей, уравнения которых с помощью преобразования координат могут быть приведены к одному из следующих видов. Эти уравнения определяют тип поверхности и называются каноническими уравнениями.
1. Эллипсоид: 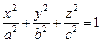
2. Конус второго порядка: 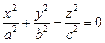
3. Гиперболоиды
1) однополостный: 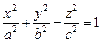 (рис. 15.3); (рис. 15.3); | 2) двуполостный: 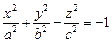 (рис. 15.4). (рис. 15.4). |
Рис. 15.3 Рис. 15.4
4. Параболоиды
1) эллиптический: 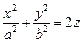 (рис. 15.5); (рис. 15.5); | 2) гиперболический: 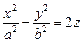 (рис.15.6). (рис.15.6). |
 |  |
Рис. 15.5 Рис. 15.6
5. Цилиндры
1) эллиптический: 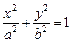 (рис. 15.7); (рис. 15.7); | 2) гиперболический: 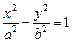 (рис. 15.8); (рис. 15.8); |
 |  |
Рис. 15.7 Рис. 15.8
3) параболический: 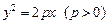
Основным методом исследования формы поверхности является метод параллельных сечений, который состоит в следующем. Поверхность пересекается координатными плоскостями и им параллельными, а затем на основании вида полученных в сечениях линий делается вывод о типе поверхности. Таким образом можно изучать основные геометрические свойства невырожденных поверхностей второго порядка на основе их канонических уравнений.
При этом, когда в общем уравнении поверхности коэффициенты 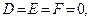
В определенных случаях уравнение (15.22) поверхности может быть приведено к уравнениям, задающим, так называемые, вырожденные поверхности. Приведем примеры таких случаев:

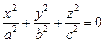
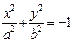
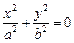
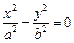
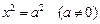
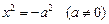

Пример 1. Привести уравнение к каноническому виду и определить тип поверхности, которую оно задает:
1)
2)
3)
4)
Решение. 1) Воспользуемся методом выделения полных квадратов.
Преобразуем левую часть уравнения:
Значит, заданное уравнение равносильно уравнению
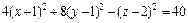
Имеем уравнение однополостного гиперболоида, центр которого находится в точке (–1, 1, 2). Его ось симметрии – прямая, параллельная оси Oz и проходящая через точку (–1, 1, 2).
2) Поскольку
то заданное уравнение равносильно уравнению
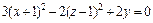
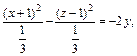
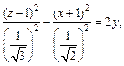
3) Выделяем полные квадраты в выражении, стоящем в левой части уравнения:
Поэтому заданное уравнение принимает вид:
или (после деления на 36)
Это уравнение эллипсоида с центром в точке (3, – 1, 2).
4. Методом выделения полных квадратов уравнение 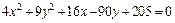
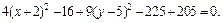
Почленное деление на 36 дает:
Это уравнение эллиптического цилиндра, смещенного в точку
(–2, 5, 0).
Пример 2. Исследовать поверхность методом сечений и построить ее:
Решение. Для исследования геометрических свойств и формы поверхности используем метод сечений.
Определим сечение поверхности плоскостями 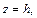
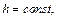
Очевидно, что это кривые, проекции которых на ось Oxy задаются уравнением
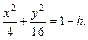
Уравнение (15.23) при 
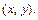
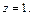
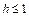
с полуосями 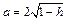
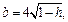
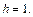
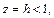
Дальнейшее уточнение формы можно получить, рассматривая сечения координатными плоскостями Oxz и Oyz:
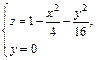
В первом случае имеем кривую 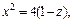
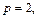
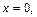
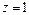
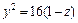
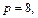
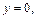
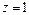
Выполненное исследование позволяет построить заданную поверхность (рис. 15.10). Это эллиптический параболоид 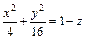
Пример 3. Построить тело, ограниченное поверхностями
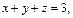
Решение. Уравнение 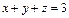
т. е. плоскость пересекает координатные оси в точках (3, 0, 0), (0, 3, 0) и (0, 0, 3) соответственно.
Уравнение 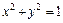
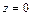
Сделаем рисунок тела (рис. 15.11, 15.12), ограниченного заданными поверхностями.
💥 Видео
Лекция. Гиперболоиды, параболоиды, конус. Исследование методом сечений.Скачать

Практическое занятие: поверхности второго порядкаСкачать

Сопротивление материалов. Лекция: метод сеченийСкачать

Метод сеченийСкачать

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Тех.Мех. - это просто. 1 Метод сеченийСкачать

Определение конических сечений 1Скачать

Математика это не ИсламСкачать

§31.1 Приведение уравнения кривой к каноническому видуСкачать

2013 1 Метод сечений Часть 1Скачать

Семинар №9 "Приведение уравнения второго порядка к каноническому виду"Скачать

Семинар Аналитическая геометрия. Кривые и поверхности второго порядка.Скачать

§64 Поверхности вращенияСкачать

СМ -1.7 Метод сечений, внутренние силовые факторы (ВСФ)Скачать

Эллипс, парабола и гипербола. Конические сечения | Ботай со мной #055 | Борис Трушин |Скачать

Поверхности 2 порядкаСкачать

Метод сечений (РОЗУ)Скачать