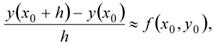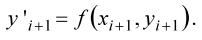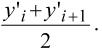Метод рунге кутта для дифференциальных уравнений 2 порядка (8 видео)

Численные методы решения обыкновенных дифференциальных уравнений. Метод Эйлера и методы Рунге-Кутта для решения дифференциальных уравнений

Суть метода Эйлера заключается в переходе от бесконечно малых приращений в уравнении к конечным: 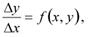(1)

т.е. в замене производной приближенным конечно-разностным отношением:

где h = ∆х — шаг интегрирования.

Отсюда 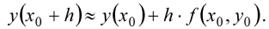(3)

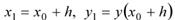
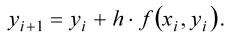
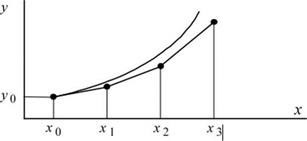
Рассматривая приближенное решение в точке как новые начальные условия, можно по формуле (3) найти значение искомой функции у(х) в следующей точке. В общем случае формула Эйлера имеет вид: (4)

Метод Эйлера может быть интерпретирован геометрически следующим образом: функцию у(х) заменяют ломаной, представляющей собой отрезки касательных к этой функции в узлах (рис. 5.1).

Рис. 5.1. Метод Эйлера

Достоинствами метода Эйлера являются его простота и наглядность, недостатками — относительно невысокая точность (он имеет первый порядок точности) и систематическое накопление ошибки. Точность и устойчивость решения в значительной степени зависят от величины шага интегрирования. Для оценки погрешности и выбора шага может быть применена формула Рунге .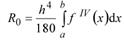

Методы Рунге-Кутта второго порядка

Методы Рунге-Кутта второго порядка основаны на разложении функции у(х) в ряд Тейлора и учете трех его первых членов (до второй производной включительно).

Метод Рунге-Кутта второго порядка с полным шагом реализуется по формуле:

(6.1.)

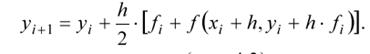
Его геометрическая интерпретация (рис. 6.1.) заключается в следующем:

1. Приближенно вычисляют значение функции в точке x_i+h по формуле Эйлера и наклон интегральной кривой в этой точке

2. Находят средний наклон на шаге h:

3. По этому наклону уточняют значение y_i₊₁ по формуле (6.1.).

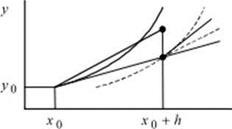Метод рунге кутта для дифференциальных уравнений 2 порядка

Рис. 6.1. Метод Рунге-Кутта второго порядка с полным шагом

Формула метода Рунге-Кутта второго порядка с половинным шагомимеет вид

Рисунок 6.3. Метод Рунге-Кутта второго порядка с половинным шагом

Метод Рунге-Кутта четвертого порядка

Содержание

Метод Рунге-Кутта решения диф. уравнений и их систем.
Ссылки
Оставить комментарий
Комментарии
Метод Рунге — Кутты
🔥 Видео

Видео:Методы численного анализа - Метод Рунге-Кутта для ОДУ 2 порядкаСкачать

Метод Рунге-Кутта решения диф. уравнений и их систем.

Метод позволяет решать системы обыкновенных дифференциальных уравнений (ОДУ) первого порядка следующего вида:

которые имеют решение:

где t — независимая переменная (например, время); X, Y и т.д. — искомые функции (зависимые от t переменные). Функции f, g и т.д. — заданы. Также предполагаются заданными и начальные условия, т.е. значения искомых функций в начальный момент.

Одно диф. уравнение — частный случай системы с одним элементом. Поэтому, далее речь пойдет для определенности о системе уравнений.

Метод может быть полезен и для решения диф. уравнений высшего (второго и т.д.) порядка, т.к. они могут быть представлены системой диф. уравнений первого порядка.

Метод Рунге-Кутта заключается в рекурентном применении следующих формул:

Реализация Метода Рунге-Кутта на Delphi может выглядеть так (привожу полностью модуль):

Модуль полностью работоспособен. Возвращаемое функцией Runge_Kutt значение — код ошибки. Вы можете дополнить список ошибок по своему усмотрению. Рассчитанные функции системы помещаются в массив Res. Чтобы не загромождать код, в модуле опущены проверки (типа блоков try). Рекомендую их добавить по своему усмотрению.

Ниже приводится описание функции Runge_Kutt и типов, использующихся в модуле.

FunArray — вектор функций (правых частей уравнений системы);
First, Last — начальная и конечная точки расчетного интервала;
Steps — число шагов по расчетному интервалу;
InitArray — вектор начальных значений
var Res — матрица результатов включая независимую переменную.

В модуле описаны типы:

Функция возвращает коды ошибок:

0 — нет ошибок;
100 — число уравнений не равно числу начальных условий.

Решение содержится в переменной-матрице Res. Первый индекс матрицы относится к переменной (0 — независимая переменная, 1 — первая зависимая и т.д.), второй — к номеру расчетной точки (0 — начальная точка).

Рассмотрим один пример использования модуля. Создадим новое приложение и подключим к нему модуль. На форме приложения разместим кнопку Button1 и область текста Memo1. Поместим в приложение две функции и обработчик нажатия кнопки:

Нажатие кнопки приведет к расчету точек системы, которые будут выведены в текстовую область.

Модуль с примером и справкой можно скачать бесплатно по адресу RK.zip (ZIP, 15,3Kb) (русский вариант). Английский вариант (условно-бесплатный) можно скачать по адресу RK_Eng.zip (ZIP, 23.4Kb)

Видео:Метод Рунге Кутты 2 и 4 порядковСкачать

Ссылки

http://sadovoya.narod.ru/RK.zip (русский вариант).
http://sintreseng.narod.ru/RK_Eng.zip (английский, условно-бесплатный вариант)

Видео:3_11. Алгоритм Рунге-КуттыСкачать

Оставить комментарий

Видео:Решение ОДУ: метод Рунге КуттаСкачать

Скачала по Вашей ссылке русский вариант, изменила для своей системы диф. уравнений, но при запуске выдаёт ошибку :
Project Ex.exe raised exception class EOverflow with message ‘ Floating point overflow ‘
Помогите, пожалуйста .

Вот изменённый мною модуль:

unit Unit1;
interface
uses
SysUtils, Forms, StdCtrls, Controls, Classes, Dialogs, Math;
type
TForm1 = class(TForm)
Memo1: TMemo;
rk_But: TButton;
procedure rk_ButClick(Sender: TObject);
private

public

end;
var
Form1: TForm1;
pn,k,ro,Pzv: Extended;

implementation
uses rk_method, Windows;

procedure Syst (var t: TFloat; var X: TFloatVector;
var RP: TFloatVector);
const
fdr1=0.503;
fdr2=0.503;
fdr3=0.196;
W1=179.8928;
W2=3773.8568;
W3=2504.1203;
b1=55.9203;
b2=98.6;
b3=98.6;
Ls1=3.78;
Ls2=9;
Ls3=15.3;
Svidj2=1352.438;
Svidj3=1352.438;
my=0.62;
vk=30;
m=1.2;
L1=30.969;
L2=42.131;
delta1=0;

begin
pn:=2.5*Power(10,4);
k:=6*Power(10,-7);
ro:=8.5*Power(10,-7);
Pzv:=3.919*Power(10,7);

RP[0] := (1/(k*W1))*(my*fdr1*sqrt(2/ro)*sqrt(Abs(pn-X[0]))-my*fdr2*sqrt(2/ro)*sqrt(Abs(X[0]-X[1]))-(delta1*delta1*delta1*b1)/(12*ro*vk*Ls1)*X[0]); // dp1/dt
RP[1] := (1/(k*W2))*(my*fdr2*sqrt(2/ro)*sqrt(Abs(X[0]-X[1]))-my*fdr3*sqrt(2/ro)*sqrt(Abs(X[1]-X[2]))-(X[4]*X[4]*X[4]*b2)/(12*ro*vk*Ls2)*X[1]); // dp2/dt
RP[2] := (1/(k*W3))*(my*fdr3*sqrt(2/ro)*sqrt(Abs(X[1]-X[2]))-(X[6]*X[6]*X[6]*b3)/(12*ro*vk*Ls3)*X[2]); // dp3/dt;
RP[3] := (((Svidj2*X[1]*(L1+L2))/L1)-Pzv)*(2/m); // dv2/dt
RP[4] := X[3]; // d delta2/dt
RP[5] := (((Svidj3*X[2]*(L1+L2))/L2)-Pzv)*(2/m); // dv3/dt
RP[6] := X[5]; // d delta3/dt
end;

procedure TForm1.rk_ButClick(Sender: TObject);
var
I, t1, t2: Cardinal;
tOut, InitConds: TFloatVector;
XOuts: TFloatMatrix;
Points: Cardinal;
First, Last: TFloat;
StepsFact: Cardinal;
Count: Word;
begin
Memo1.Clear;
First := 0.0;
Last := 10.0;
Count:= 7;
Points:=10+1; //11 points for output
StepsFact:=1000000; //all steps inside function = 10*StepsFact

try
SetLength(InitConds, Count);
InitConds[0]:=0.0; //x0(0)=0
InitConds[1]:=0.0; //x1(0)=0
InitConds[2]:=0.0; //x2(0)=0
InitConds[3]:=0.0; //x3(0)=0
InitConds[4]:=0.0; //x4(0)=0
InitConds[5]:=0.0; //x5(0)=0
InitConds[6]:=0.0; //x6(0)=0

SetLength(tOut, Points);
SetLength(XOuts, Count, Points);
except
ShowMessage(‘Out of memory. ‘);
exit;
end;

Видео:Явный метод Рунге-Кутты второго порядка для решения задачи Коши. Контрольная работа МФТИСкачать

Метод Рунге — Кутты

Этот онлайн калькулятор реализует классический метод Рунге — Кутты (встречается также название метод Рунге — Кутта) четвертого порядка точности. Метод используется для решения дифференциальных уравнений первой степени с заданным начальным значением

Калькулятор ниже находит численное решение дифференциального уравнения первой степени методом Рунге-Кутты (иногда встречается название метод Рунге-Кутта, а в поисковиках бывает ищут «метод рунге кута», «метод рунги кутта» и даже «метод рунги кута»), который также известен как классический метод Рунге — Кутты (потому что есть на самом деле семейство методов Рунге-Кутты) или метод Рунге — Кутты четвертого порядка.

Для того, чтобы использовать калькулятор, вам надо привести дифференциальное уравнение к форме

и ввести правую часть уравнения f(x,y) в поле y’ калькулятора.

Также вам понадобится ввести начальное значение

и указать точку в которой вы хотите получить численное решение уравнения .

Последнее параметр калькулятора — размер шага с которым вычисляется следующее приближение по графику функции.

Описание метода можно найти под калькулятором.