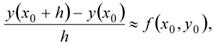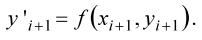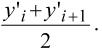Метод рунге кутта 4 порядка в уравнение эйлера (3 видео)

Численные методы решения обыкновенных дифференциальных уравнений. Метод Эйлера и методы Рунге-Кутта для решения дифференциальных уравнений

Суть метода Эйлера заключается в переходе от бесконечно малых приращений в уравнении к конечным: 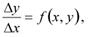(1)

т.е. в замене производной приближенным конечно-разностным отношением:

где h = ∆х — шаг интегрирования.

Отсюда 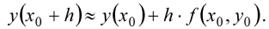(3)

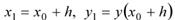
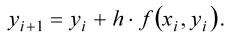
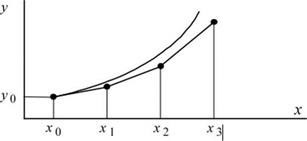
Рассматривая приближенное решение в точке как новые начальные условия, можно по формуле (3) найти значение искомой функции у(х) в следующей точке. В общем случае формула Эйлера имеет вид: (4)

Метод Эйлера может быть интерпретирован геометрически следующим образом: функцию у(х) заменяют ломаной, представляющей собой отрезки касательных к этой функции в узлах (рис. 5.1).

Рис. 5.1. Метод Эйлера

Достоинствами метода Эйлера являются его простота и наглядность, недостатками — относительно невысокая точность (он имеет первый порядок точности) и систематическое накопление ошибки. Точность и устойчивость решения в значительной степени зависят от величины шага интегрирования. Для оценки погрешности и выбора шага может быть применена формула Рунге .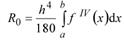

Методы Рунге-Кутта второго порядка

Методы Рунге-Кутта второго порядка основаны на разложении функции у(х) в ряд Тейлора и учете трех его первых членов (до второй производной включительно).

Метод Рунге-Кутта второго порядка с полным шагом реализуется по формуле:

(6.1.)

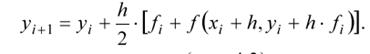
Его геометрическая интерпретация (рис. 6.1.) заключается в следующем:

1. Приближенно вычисляют значение функции в точке x_i+h по формуле Эйлера и наклон интегральной кривой в этой точке

2. Находят средний наклон на шаге h:

3. По этому наклону уточняют значение y_i₊₁ по формуле (6.1.).

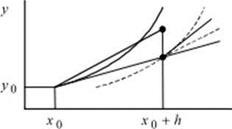Метод рунге кутта 4 порядка в уравнение эйлера

Рис. 6.1. Метод Рунге-Кутта второго порядка с полным шагом

Формула метода Рунге-Кутта второго порядка с половинным шагомимеет вид

Рисунок 6.3. Метод Рунге-Кутта второго порядка с половинным шагом

Метод Рунге-Кутта четвертого порядка

Видео:4a. Методы Рунге-КуттаСкачать

Метод Рунге-Кутты 4-го порядка для решения дифференциального уравнения

Учитывая следующие входные данные,

Обычное дифференциальное уравнение, которое определяет значение dy / dx в виде x и y.
Начальное значение y, т. Е. Y (0)

Таким образом, мы приведены ниже.

Задача состоит в том, чтобы найти значение неизвестной функции y в заданной точке x.

Метод Рунге-Кутты находит приблизительное значение y для данного x. Только обыкновенные дифференциальные уравнения первого порядка могут быть решены с помощью метода 4-го порядка Рунге Кутты.

Ниже приведена формула, используемая для вычисления следующего значения y _{n + 1} из предыдущего значения y _n . Значения n равны 0, 1, 2, 3,… (x — x0) / h. Здесь h — высота шага, а x _{n + 1} = x ₀ + h

, Меньший размер шага означает большую точность.

Формула в основном вычисляет следующее значение y _{n + 1,} используя текущее значение y _n плюс средневзвешенное значение четырех приращений.

k ₁ — приращение, основанное на наклоне в начале интервала, используя y
K ₂ представляет собой приращение на основе наклона в средней точке интервала, с использованием Y + ₁ HK / 2.
к ₃ снова приращение на основе наклона в средней точке, используя при помощи у + кк _2/2.
k ₄ — это приращение, основанное на наклоне в конце интервала, с использованием y + hk ₃ .

Этот метод является методом четвертого порядка, это означает, что локальная ошибка усечения имеет порядок O (h 5 ), в то время как общая накопленная ошибка составляет порядок O (h 4 ).

Ниже приведена реализация приведенной выше формулы.

// C программа для реализации метода Рунге Кутты
#include

// Пример дифференциального уравнения «dy / dx = (x — y) / 2»

float dydx( float x, float y)

// Находит значение y для заданного x, используя размер шага h
// и начальное значение y0 в x0.

float rungeKutta( float x0, float y0, float x, float h)

// Подсчитать количество итераций, используя размер шага или

int n = ( int )((x — x0) / h);

float k1, k2, k3, k4, k5;

// Итерация по количеству итераций

// Применить формулы Рунге Кутты, чтобы найти

// следующее значение у

k2 = h*dydx(x0 + 0.5*h, y + 0.5*k1);

k3 = h*dydx(x0 + 0.5*h, y + 0.5*k2);

k4 = h*dydx(x0 + h, y + k3);

// Обновить следующее значение y

y = y + (1.0/6.0)*(k1 + 2*k2 + 2*k3 + k4);;

// Обновляем следующее значение x

float x0 = 0, y = 1, x = 2, h = 0.2;

printf ( «nThe value of y at x is : %f» ,

rungeKutta(x0, y, x, h));

// Java-программа для реализации метода Рунге Кутты

double dydx( double x, double y)

// Находит значение y для заданного x, используя размер шага h

// и начальное значение y0 в x0.

double rungeKutta( double x0, double y0, double x, double h)

differential d1 = new differential();

// Подсчитать количество итераций, используя размер шага или

int n = ( int )((x — x0) / h);

double k1, k2, k3, k4, k5;

// Итерация по количеству итераций

for ( int i = 1 ; i

// Применить формулы Рунге Кутты, чтобы найти

// следующее значение у

k1 = h * (d1.dydx(x0, y));

k2 = h * (d1.dydx(x0 + 0.5 * h, y + 0.5 * k1));

k3 = h * (d1.dydx(x0 + 0.5 * h, y + 0.5 * k2));

k4 = h * (d1.dydx(x0 + h, y + k3));

// Обновить следующее значение y

y = y + ( 1.0 / 6.0 ) * (k1 + 2 * k2 + 2 * k3 + k4);

// Обновляем следующее значение x

public static void main(String args[])

differential d2 = new differential();

double x0 = 0 , y = 1 , x = 2 , h = 0.2 ;

System.out.println( «nThe value of y at x is : «

+ d2.rungeKutta(x0, y, x, h));

// Этот код предоставлен Prateek Bhindwar

# Программа Python для реализации метода Рунге Кутты
# Пример дифференциального уравнения «dy / dx = (x — y) / 2»

# Находит значение y для заданного x, используя размер шага h
# и начальное значение y0 при x0.

def rungeKutta(x0, y0, x, h):

# Подсчитать количество итераций, используя размер шага или

n = ( int )((x — x0) / h)

# Итерировать по количеству итераций

for i in range ( 1 , n + 1 ):

«Apply Runge Kutta Formulas to find next value of y»

k1 = h * dydx(x0, y)

k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1)

k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2)

k4 = h * dydx(x0 + h, y + k3)

# Обновить следующее значение y

y = y + ( 1.0 / 6.0 ) * (k1 + 2 * k2 + 2 * k3 + k4)

# Обновить следующее значение x

print ‘The value of y at x is:’ , rungeKutta(x0, y, x, h)

# Этот код предоставлен Prateek Bhindwar

// C # программа для реализации Runge
// метод Кутты

static double dydx( double x, double y)

// Находит значение y для данного x

// используя размер шага h и начальный

// значение y0 в x0.

static double rungeKutta( double x0,

double y0, double x, double h)

// Подсчитать количество итераций используя

// размер шага или высота шага h

int n = ( int )((x — x0) / h);

double k1, k2, k3, k4;

// Итерация по количеству итераций

for ( int i = 1; i

// Применяем формулы Рунге Кутты

// найти следующее значение у

k1 = h * (dydx(x0, y));

k2 = h * (dydx(x0 + 0.5 * h,

k3 = h * (dydx(x0 + 0.5 * h,

k4 = h * (dydx(x0 + h, y + k3));

// Обновить следующее значение y

y = y + (1.0 / 6.0) * (k1 + 2

// Обновляем следующее значение x

public static void Main()

double x0 = 0, y = 1, x = 2, h = 0.2;

Console.WriteLine( «nThe value of y»

+ rungeKutta(x0, y, x, h));

// Этот код предоставлен Sam007.

// PHP-программа для реализации
// метод Рунге Кутта

// Пример дифференциального уравнения
// «dy / dx = (x — y) / 2»

function dydx( $x , $y )

return (( $x — $y ) / 2);

// Находит значение y для
// дано х, используя размер шага h
// и начальное значение y0 в x0.

function rungeKutta( $x0 , $y0 , $x , $h )

// Подсчитать количество итераций

// используя размер шага или шаг

$k1 ; $k2 ; $k3 ; $k4 ; $k5 ;

// Итерация по номеру

for ( $i = 1; $i $n ; $i ++)

// Применить Рунге Кутта

// формулы для поиска

// следующее значение у

$k1 = $h * dydx( $x0 , $y );

$k2 = $h * dydx( $x0 + 0.5 * $h ,

$k3 = $h * dydx( $x0 + 0.5 * $h ,

$k4 = $h * dydx( $x0 + $h , $y + $k3 );

// Обновить следующее значение y

$y = $y + (1.0 / 6.0) * ( $k1 + 2 *

// Обновляем следующее значение x

echo «The value of y at x is : » ,

rungeKutta( $x0 , $y , $x , $h );

// Этот код предоставлен anuj_67.
?>

Сложность по времени вышеупомянутого решения составляет O (n), где n — (x-x0) / ч.

Некоторые полезные ресурсы для подробных примеров и большего количества объяснения.
http://w3.gazi.edu.tr/

Эта статья предоставлена Арпит Агарвал . Если вам нравится GeeksforGeeks и вы хотите внести свой вклад, вы также можете написать статью и отправить ее по почте на contrib@geeksforgeeks.org. Смотрите свою статью, появляющуюся на главной странице GeeksforGeeks, и помогите другим вундеркиндам.

Пожалуйста, напишите комментарии, если вы обнаружите что-то неправильное, или вы хотите поделиться дополнительной информацией по обсуждаемой теме

Видео:Решение ОДУ методом Рунге-Кутта 4 порядка (программа)Скачать

7.4. Метод Рунге-Кутта 4 порядка

На практике наибольшее распространение получил метод Рунге-Кутта 4-го порядка, в котором усреднение проводится по трём точкам, формула Эйлера на каждом отрезке используется 4 раза: в начале отрезка, дважды в его середине и в конце отрезка.

Расчетные формулы метода для дифференциального уравнения (7.3) имеют вид:

, (7.8)

Где i = 0, 1, …., n-1 — номер узла;

Xi = a + i×h — координата узла;

У0 = у(х0) — начальное условие.

Погрешность метода dМ = О(h5).

Схема алгоритма решения ОДУ методом Рунге-Кутта 4-го порядка отличается алгоритмом расчёта новой точки (Рис. 7.5).

Пример 7.4. Решение ранее рассмотренного уравнения (пример 7.1) методом Рунге-Кутта 4 порядка.

Y’ — 2×y + x2 = 1, x Î [0;1], y(0) = 1.

Пусть n = 10 , h = (1 — 0)/10 = 0,1.

Начальная точка x0 = 0, y0 = 1.

Рассчет первой точки.

Сначала вычислим значения C0, C1, C2, C3:

Вычислим значение y1:

Аналогично можно вычислить значения функции во 2, 3, . , 10 точках.

Рис. 7.7. Схема алгоритма расчета новой точки методом Рунге-Кутта 4-го порядка.

Общая характеристика методов:

1. Все методы являются Одношаговыми, то есть для вычисления значения функции в новой точке используется ее значение в предыдущей точке. Это свойство называется Самостартованием.

2. Все методы легко обобщаются на системы дифференциальных уравнений 1-го порядка.