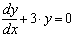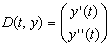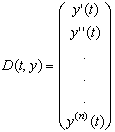Построение решений обыкновенных дифференциальных уравнений
Решение дифференциального уравнения 1-го порядка


Простой метод Эйлера реализуется применением на каждом шаге вычислений следующих итерационных выражений:
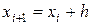
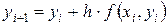
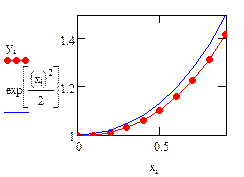
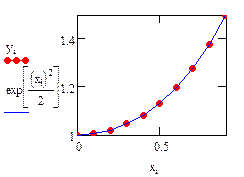
Рассмотрим реализацию метода в MathCADна примере уравнения:
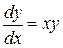
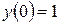
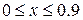
Аналитическое решение известно и имеет вид:

Краткие сведения о составлении программ в MathCAD
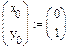
Графиквставляется командой Insert→ Graph→ X-YPlotили клавишей «@».
Для удобства в работе рекомендуется отключить автоматическое вычисление, убрав галочку с опции меню Tools→ Calculate→ AutomaticCalculation. Тогда расчет не будет выполняться в ходе набора программы, а запуститься только после нажатия кнопки Calculate, расположенной на панели инструментов (в виде значка 
Ниже приведена расчетная программа. Повторите её. Получите графики с тем же форматом линий. Формат линий графика можно изменить, открыв с помощью ПК мыши контекстное меню и выбрав Format… → Traces.
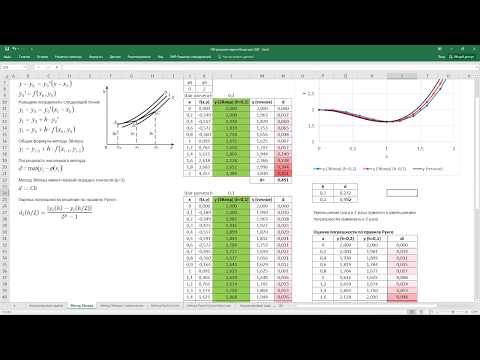
Программа для простого метода Эйлера
 |
| Шаг изменения x |
 |
| Число шагов |
 |
| Функция, определяющая производную |
 |
| Задание цикла |
 |
| Задание начальных условий |
 |
| Итерационные уравнения |
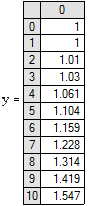
| Результаты решения: |
 |
 |
 |
 |
Следующая программа реализует модифицированный метод Эйлера. Отличие от простого метода заключается в итерационных уравнениях.
Программа для модифицированного метода Эйлера
 |
| Шаг изменения x |
 |
| Число шагов |
 |
| Функция, определяющая производную |
 |
| Задание цикла |
 |
| Задание начальных условий |
| Итерационные уравнения |
 |
| Результаты решения: |
 |
 |
 |
 |
Метод Рунге-Кутта 4-го порядка используется в тех случаях, когда необходима высокая точность расчетов, недостигаемая методами Эйлера.
Программа для метода Рунге-Кутта
 |
| Шаг изменения x |
 |
| Число шагов |
 |
| Функция, определяющая производную |
| Задание коэффициентов k1, k2, k3, k4 как функций пользователя: |
 |
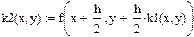 |
 |
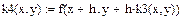 |
 |
| Усредненная функция |
 |
| Задание цикла |
 |
| Задание начальных условий |
 |
| Итерационные уравнения |
| Результаты решения: |
 |
 |
 |
 |
Решение дифференциальных уравнений 2-го порядкаметодом Рунге-Кутта.
Подход к реализации метода основан на использовании дополнительной функции 


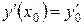
Преобразуем задачу к системе из двух уравнений:


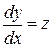

Тогда получим следующее обобщение итерационной схемы:



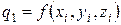
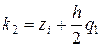




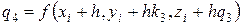
Отметим, что значения на каждом следующем шаге рассчитываются по значениям, полученным на предыдущем. Кроме того, использованы прежние правила «взвешивания» коэффициентов при усреднении.
Пример математической модели с дифференциальным уравнением 2-го порядка
Рассмотрим уравнение колебательного процесса при наличии внешнего периодического воздействия:

где t– время, и искомой является зависимость 
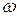
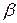
Если 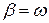

где Aи 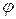
Когда 

В этом случае колебательный процесс слагается из собственных колебаний с частотой 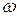
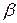
Моделирование резонансных колебаний
Методом Рунге-Кутта найдем решение задачи:

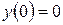


Согласно изложенной выше теории, аналитическое решение уравнения имеет вид:
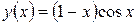
Ниже приведен алгоритм расчета и его реализация в MathCAD.
Программа расчета резонансных колебаний методом Рунге-Кутта
 |
| Шаг изменения x |
 |
| Число шагов |
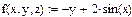 |
| Функция в системе уравнений dy/dx = z и dz/dx = f(x,y,z) |
| Задание коэффициентов как функций пользователя: |
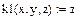 |
 |
 |
 |
 |
 |
 |
 |
| Усредненные функции: |
 |
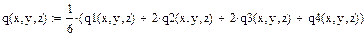 |
 |
| Задание цикла |
 |
| Задание начальных условий |
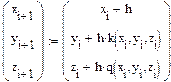 |
| Итерационные уравнения |
 |
| Результаты решения: |
Задание для самостоятельного выполнения
Найти решение уравнения вынужденных колебаний:

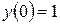
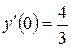
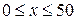
Решение представить в виде графика. Для сравнения привести и график точного решения (также как это было сделано для резонансных колебаний).
Видео:Программируем метод Рунге-Кутта 4 порядкаСкачать

Тема 7. Решение дифференциальных уравнений и систем в MathCad
Краткие теоретические сведения
Для решения дифференциальных уравнений с начальными условиями система Mathcad имеет ряд встроенных функций:
rkfixed – функция для решения ОДУ и систем ОДУ методом Рунге–Кутта четвертого порядка с постоянным шагом;
Rkadapt – функция решения ОДУ и систем ОДУ методом Рунге–Кутта с переменным шагом;
Odesolve – функция, решающая ОДУ блочным методом.
Ниже приведено описание стандартной функции rkfixed с указанием параметров функции.
y – вектор начальных условий из k элементов ( k – количество уравнений в системе);
x1 и x2 – левая и правая границы интервала, на котором ищется решение ОДУ или системы ОДУ;
p – число точек внутри интервала (x1, x2), в которых ищется решение;
D – вектор, состоящий из k-элементов, который содержит первую производную искомой функции или первые производные искомых функций, если речь идет о решении системы.
Результатом работы функции является матрица из p +1 строк, первый столбец которой содержит точки, в которых получено решение, а остальные столбцы – сами решения.
На рисунке 2.7.1 приведены конкретные примеры решения различных дифференциальных уравнений и систем ОДУ в MathCAD .
Рисунок 2.7.1 – Примеры решения дифференциальных уравнений и систем
При решении дифференциального уравнения первого порядка нужно создать вектор начальных условий из одного элемента Y 1 , который затем используется при формировании вектора-функции правой части дифференциального уравнения. При обращении к функции rkfixed указывается имя вектора Y , границы интервала, на котором ищется решение уравнения, например, (0 ; 2), количество точек, в которых ищется решение – 100, вектор-функция, описывающая правую часть дифференциального уравнения – D . В результате получается матрица z , в первом столбце которой содержатся значения аргумента искомой функции, во втором – значения самой результирующей функции. При построении графика функции первый столбец полученной матрицы указывается как аргумент, второй столбец – как функция.
При решении системы дифференциальных уравнений нужно создать вектор начальных условий из двух элементов, например, вектор v , который затем используется при формировании вектора-функции правой части дифференциального уравнения. При обращении к функции rkfixed указывается имя вектора v , и границы интервала, на котором ищется решение уравнения, например, (0 ; 5), количество точек, в которых ищется решение – 100, вектор-функция, описывающая правую часть дифференциального уравнения – D . В результате получается матрица s , в первом столбце которой содержатся значения аргумента искомых функций, во втором и третьем столбцах – значения самих функций при соответствующем значении аргумента. При построении графика можно воспользоваться первым столбцом полученной матрицы как аргументом, а вторым и третьим столбцами – как функциями.
На рисунке 2.7.2 приведен пример решения дифференциального уравнения второго порядка с использованием функции rkfixed . Необходимо решить дифференциальное уравнение второго порядка с заданными начальными условиями вида:
Рисунок 2.7.2 – Пример решения дифференциальных уравнений второго порядка с помощью rkfixed
Для решения уравнения с помощью функции rkfixed нужно выполнить замену переменных и привести дифференциальное уравнение второго порядка к двум дифференциальным уравнениям первого порядка. Вид этих уравнений приведен ниже.
Документ формируется точно так же, как и при решении системы ОДУ.
На рисунке 2.7.2 показана возможность вычисления вектора второй производной найденной функции – вектора а, построены графики исходной функции, функций первой и второй производных.
Практическая часть темы 7
7.1 Решение дифференциальных уравнений первого порядка
Последовательность действий для р ешения дифференциального уравнения первого порядка такова:
q сформировать вектор начальных условий из одного элемента, присвоив начальное значение искомой функции переменной с индексом, например: 

q определить вектор-функцию из одного элемента, которая содержит первую производную неизвестной функции:
· набрать имя функции с двумя параметрами: первый параметр – аргумент искомой функции (независимая переменная), второй – имя вектора, содержащего искомую функцию (можно использовать имя вектора начальных условий), например, D ( x , Y );
· набрать оператор «:=» и выражение для первой производной (выразить из дифференциального уравнения), в котором вместо имени искомой функции подставлен первый элемент вектора-параметра, например, для уравнения 


q присвоить некоторой переменной значение функции rkfixed , указав в скобках следующие параметры:
· первый – имя вектора начальных условий,
· второй – левая граница интервала, на котором ищется решение, в виде числовой константы,
· третий – правая граница интервала, на котором ищется решение, в виде числовой константы,
· четвертый – количество точек, в которых ищется решение,
· пятый – имя вектора-функции, описывающего первую производную, без параметров;
например: 
(в результате получится матрица Z , в первом столбце которой содержатся значения аргумента искомой функции, во втором – значения самой функции);
q вывести матрицу, содержащую решение ДУ с помощь оператора «=», например: Z = ;
q построить график найденной функции ( см. тему 5 ), указав в качестве аргумента по оси абсцисс столбец 



Пример 7.1 Найти численное решение дифференциального уравнения первого порядка 
Выполнить графическую интерпретацию результатов.
7.2 Решение систем дифференциальных уравнений
Последовательность действий для р ешения системы дифференциальных уравнений первого порядка такова (описана для значения ORIGIN =0 ):
q перейти в исходной системе уравнений к однотипным обозначениям функций и выразить первые производные,
например, систему 

q в документе MathCad сформировать вектор начальных условий, количество элементов которого равно количеству уравнений системы, присвоив его некоторой переменной (см. тему 2);
например, 
q определить вектор-функцию, которая содержит первые производные искомых функций:
· набрать имя функции с двумя параметрами: первый параметр – аргумент искомых функций (независимая переменная), второй – имя вектора, содержащего искомые функции (можно использовать имя вектора начальных условий), например, D ( t , V );
(Замечание: если независимая переменная явно не присутствует в системе, то в качестве ее имени можно выбрать любую переменную)
· набрать оператор «:=» и вставить шаблон вектора, количество элементов которого равно количеству уравнений системы (см. тему 2)
· набрать в качестве элементов вектора правые части системы уравнений, в которых искомые функции представлены соответствующими элементами вектора-параметра, например,

q присвоить некоторой переменной значение функции rkfixed , указав в скобках следующие параметры:
· первый – имя вектора начальных условий,
· второй – левая граница интервала, на котором ищется решение, в виде числовой константы,
· третий – правая граница интервала, на котором ищется решение, в виде числовой константы,
· четвертый – количество точек, в которых ищется решение,
· пятый – имя вектора-функции, описывающего первые производные, без параметров;
например: 
(в результате получится матрица Z , в первом столбце которой содержатся значения аргумента искомых функций, во втором – значения первой функции, в третьем – значения второй функции и т. д.);
q вывести матрицу, содержащую решение системы ДУ с помощь оператора «=», например: Z = ;
q построить графики найденных функций ( см. тему 5 ), указав в качестве аргумента по оси абсцисс первый столбец матрицы решений, например, 


Пример 7.2 Найти решение системы дифференциальных уравнений
на интервале от 0 до 0.5 в 1000 точках, при следующих начальных условиях: x (0)=0.1 и y (0)=1.
Выполнить графическую интерпретацию результатов.
Видео:04 Метод Рунге-Кутты 4-го порядкаСкачать

Метод рунге кутта 4 порядка для системы уравнений в маткаде
При решении дифференциального уравнения искомой величиной является функция. Для ОДУ неизвестная функция — функция одной переменной. Дифференциальные уравнения в частных производных — это дифференциальные уравнения, в которых неизвестной является функция двух или большего числа переменных. Mathcad имеет ряд встроенных функций, предназначенных для решения ОДУ. Каждая из этих функций предназначена для численного решения дифференциального уравнения. В результате решения получается матрица, содержащая значения функции, вычисленные на некотором множестве точек (на некоторой сетке значений). Для каждого алгоритма, который используется при решении дифференциальных уравнений, Mathcad имеет различные встроенные функции. Несмотря на различные методы поиска решения, каждая из этих функций требует, чтобы были заданы по крайней мере следующие величины, необходимые для поиска решения:
- Начальные условия.
- Набор точек, в которых нужно найти решение.
- Само дифференциальное уравнение, записанное в некотором специальном виде, который будет детально описан в этой главе.
В этом разделе описано, как решить ОДУ, используя функцию rkfixed. Раздел начинается с примера того, как решить простейшее дифференциальное уравнение первого порядка. Затем будет показано, как можно решать дифференциальные уравнения более высокого порядка.
Дифференциальные уравнения первого порядка
Дифференциальное уравнение первого порядка — это уравнение, которое не содержит производных выше первого порядка от неизвестной функции. На Рисунке 1 показан пример того, как решить относительно простое дифференциальное уравнение:
с начальными условиями: y(0) = 4
Функция rkfixed на Рисунке 1 использует для поиска решения метод Рунге-Кутты четвертого порядка. В результате решения получается матрица, имеющая два следующих столбца:
- Первый столбец содержит точки, в которых ищется решение дифференциального уравнения.
- Второй столбец содержит значения найденного решения в соответствующих точках.
Рисунок 1: Решение дифференциального уравнения первого порядка.
Функция rkfixed имеет следующие аргументы:
| y = | Вектор начальных условий размерности n, где n — порядок дифференциального уравнения или число уравнений в системе (если решается система уравнений). Для дифференциального уравнения первого порядка, как, например, для уравнения, приведенного на Рисунке 1, вектор начальных значений вырождается в одну точку y0 = y(x1). |
| x1, x2 = | Граничные точки интервала, на котором ищется решение дифференциальных уравнений. Начальные условия, заданные в векторе y, — это значение решения в точке x1. |
| npoints = | Число точек (не считая начальной точки), в которых ищется приближенное решение. При помощи этого аргумента определяется число строк (1 + npoints) в матрице, возвращаемой функцией rkfixed. |
| D (x, y) = | Функция, возвращающая значение в виде вектора из n элементов, содержащих первые производные неизвестных функций. |
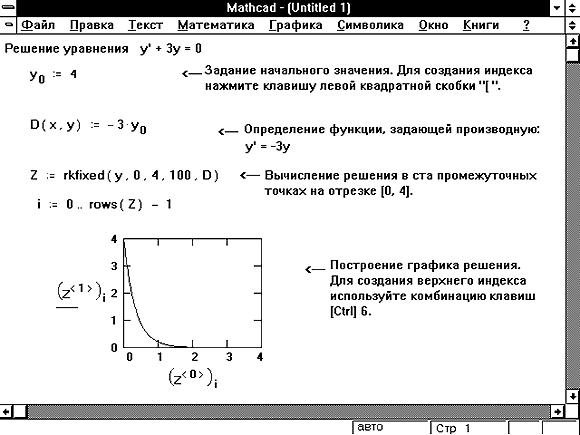
Наиболее трудная часть решения дифференциального уравнения состоит в определении функции D(x, y), которая содержит вектор первых производных от неизвестных функций. В примере, приведенном на Рисунке 1, было достаточно просто разрешить уравнение относительно первой производной , и определить функцию D(x, y). Иногда, особенно в случае нелинейных дифференциальных уравнений, это может быть трудно. В таких случаях иногда удаётся разрешить уравнение относительно в символьном виде и подставить это решение в определение для функции D(x, y). Используйте для этого команду Решить относительно переменной из меню Символика.
Рисунок 2: Более сложный пример, содержащий нелинейное дифференциальное уравнение.
Дифференциальные уравнения второго порядка
Как только Вы научились решать дифференциальное уравнение первого порядка, можно приступать к решению дифференциальных уравнений более высокого порядка. Мы начнем с дифференциального уравнения второго порядка. Основные отличия от уравнения первого порядка состоят в следующем:
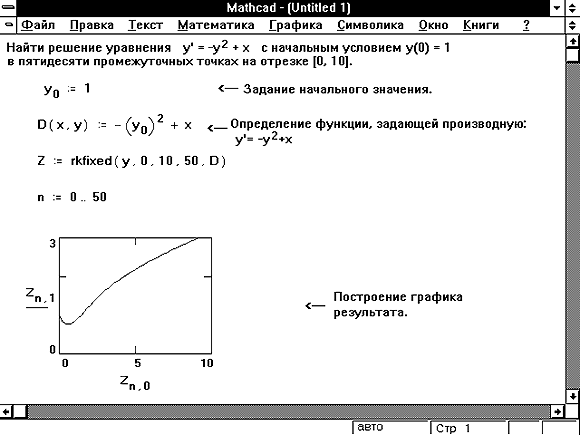
- Вектор начальных условий y теперь состоит из двух элементов: значений функции и её первой производной в начальной точке интервала x1.
- Функция D(t, y) является теперь вектором с двумя элементами:
Пример, приведенный на Рисунке 3, показывает, как решить следующее дифференциальное уравнение второго порядка:
Рисунок 3: Решение дифференциального уравнения второго порядка.
Уравнения более высокого порядка
Методика решения дифференциальных уравнений более высокого порядка является развитием методики, которая применялась для решения дифференциальных уравнений второго порядка. Основное различие состоит в следующем:
- Вектор начальных значений y теперь состоит из n элементов, определяющих начальные условия для искомой функции и ее производных y, y’ , y». y (n-1)
- Функция D является теперь вектором, содержащим n элементов:
Пример, приведенный на Рисунке 4, показывает, как решить следующее дифференциальное уравнение четвертого порядка:
с начальными условиями:
Рисунок 4: Решение дифференциального уравнения более высокого порядка.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
🎥 Видео
Решение ОДУ методом Рунге-Кутта 4 порядка (программа)Скачать

4a. Методы Рунге-КуттаСкачать

Интегрирование систем дифференциальных уравнений методом Рунге-Кутта 4-ог порядка в Arduino IDE.Скачать

6.4 Явные методы Рунге-КуттыСкачать

6.1 Численные методы решения задачи Коши для ОДУСкачать
Метод ЭйлераСкачать

Решение задачи Коши в MathCADСкачать

Численные методы решения ДУ: метод Рунге-КуттаСкачать

Решение ОДУ: метод Рунге КуттаСкачать

Метод Рунге Кутты 2 и 4 порядковСкачать

3_11. Алгоритм Рунге-КуттыСкачать

Работа с MathCad Prime. Решение дифференциальных уравнений.Скачать

Лекция 5. Методы Рунге--Кутты. 11.03.2021Скачать

Численное решение задачи Коши методом ЭйлераСкачать

Решение ОДУ методом Рунге КуттаСкачать

Тестирование метода Рунге-Кутта. Решение дифуравненийСкачать

Методы численного анализа - Метод Рунге-Кутта для ОДУ 2 порядкаСкачать