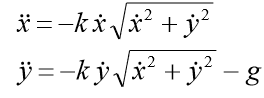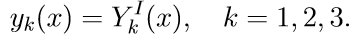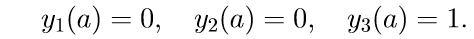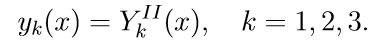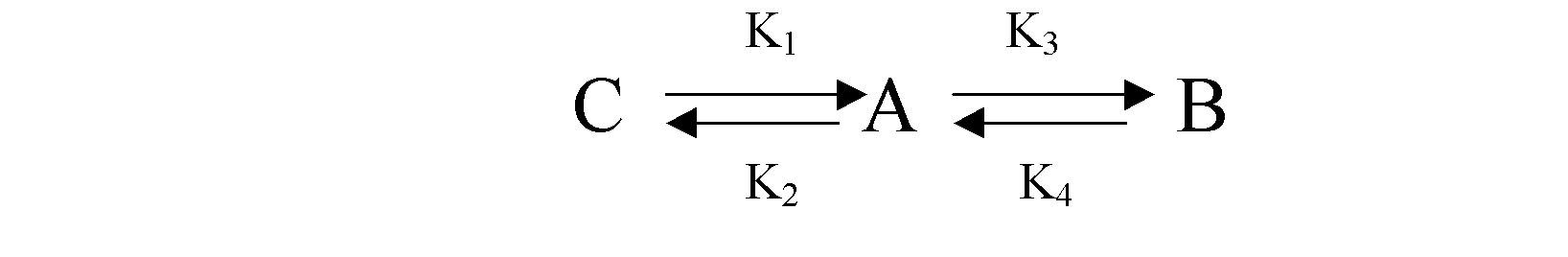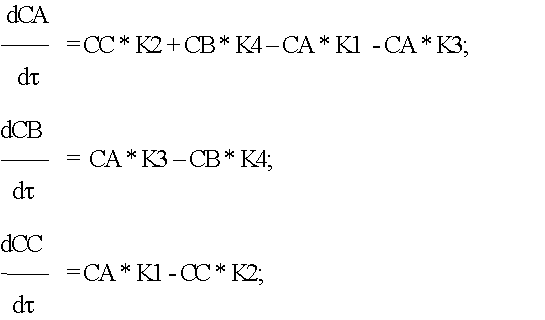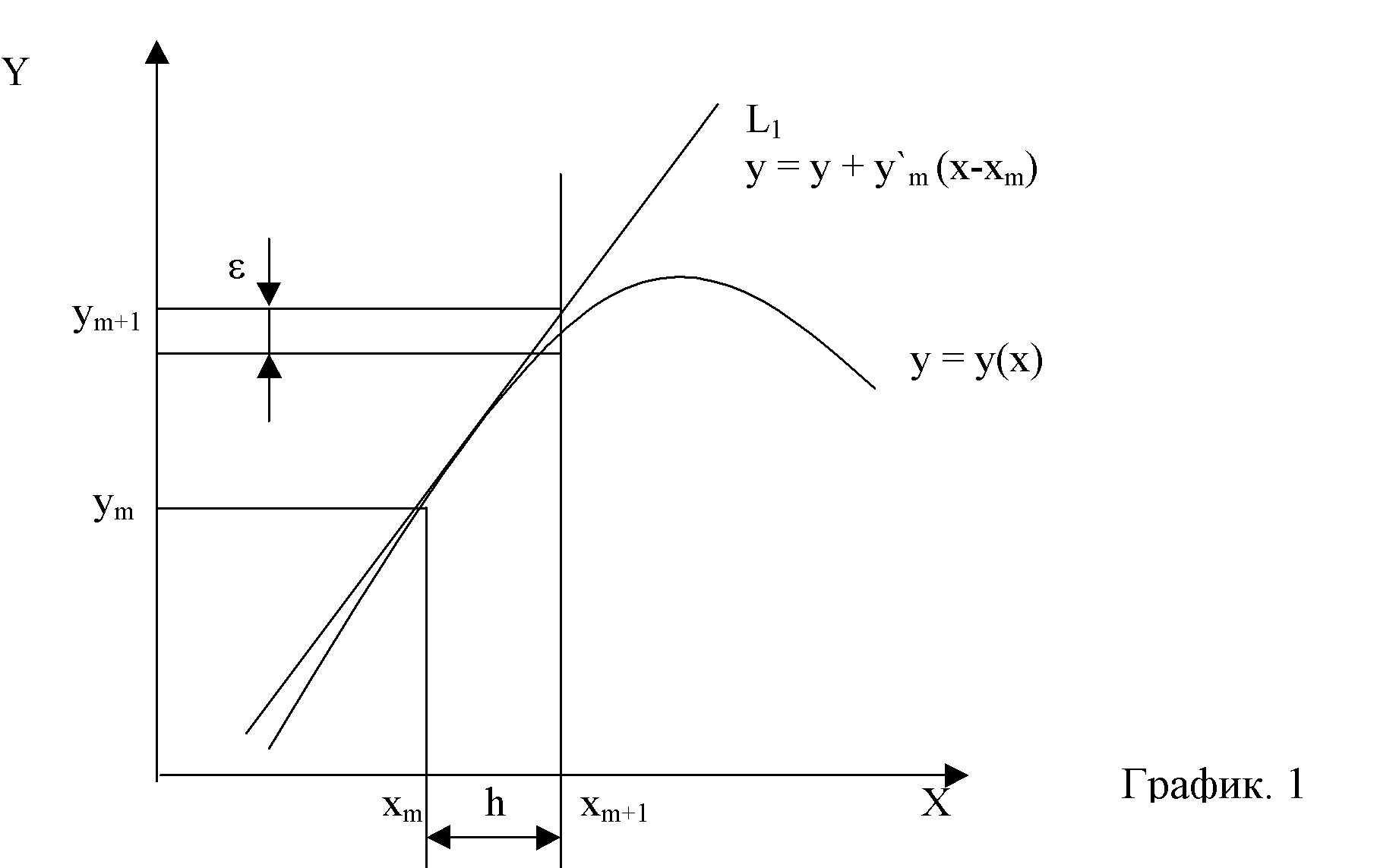Метод позволяет решать системы обыкновенных дифференциальных уравнений (ОДУ) первого порядка следующего вида:
которые имеют решение:
где t — независимая переменная (например, время); X, Y и т.д. — искомые функции (зависимые от t переменные). Функции f, g и т.д. — заданы. Также предполагаются заданными и начальные условия, т.е. значения искомых функций в начальный момент.
Одно диф. уравнение — частный случай системы с одним элементом. Поэтому, далее речь пойдет для определенности о системе уравнений.
Метод может быть полезен и для решения диф. уравнений высшего (второго и т.д.) порядка, т.к. они могут быть представлены системой диф. уравнений первого порядка.
Метод Рунге-Кутта заключается в рекурентном применении следующих формул:
Реализация Метода Рунге-Кутта на Delphi может выглядеть так (привожу полностью модуль):
Модуль полностью работоспособен. Возвращаемое функцией Runge_Kutt значение — код ошибки. Вы можете дополнить список ошибок по своему усмотрению. Рассчитанные функции системы помещаются в массив Res. Чтобы не загромождать код, в модуле опущены проверки (типа блоков try). Рекомендую их добавить по своему усмотрению.
Ниже приводится описание функции Runge_Kutt и типов, использующихся в модуле.
- FunArray — вектор функций (правых частей уравнений системы);
- First, Last — начальная и конечная точки расчетного интервала;
- Steps — число шагов по расчетному интервалу;
- InitArray — вектор начальных значений
- var Res — матрица результатов включая независимую переменную.
В модуле описаны типы:
Функция возвращает коды ошибок:
- 0 — нет ошибок;
- 100 — число уравнений не равно числу начальных условий.
Решение содержится в переменной-матрице Res. Первый индекс матрицы относится к переменной (0 — независимая переменная, 1 — первая зависимая и т.д.), второй — к номеру расчетной точки (0 — начальная точка).
Рассмотрим один пример использования модуля. Создадим новое приложение и подключим к нему модуль. На форме приложения разместим кнопку Button1 и область текста Memo1. Поместим в приложение две функции и обработчик нажатия кнопки:
Нажатие кнопки приведет к расчету точек системы, которые будут выведены в текстовую область.
Модуль с примером и справкой можно скачать бесплатно по адресу RK.zip (ZIP, 15,3Kb) (русский вариант). Английский вариант (условно-бесплатный) можно скачать по адресу RK_Eng.zip (ZIP, 23.4Kb)
- Ссылки
- Оставить комментарий
- Комментарии
- Численное решение математических моделей объектов заданных системами дифференциальных уравнений
- Введение:
- Краткие теоретические и фактические данные по рассматриваемым методам и программным средствам для численного решения СДУ
- Вычислительный эксперимент по определению абсолютной погрешности численного решения нелинейного дифференциального уравнения с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
- Численный эксперимент по сравнению быстродействия численного решения СДУ при использовании функции ode с атрибутом dopri5 (метод Рунге – Кутты 5 порядка) и с использованием адаптированного к Python метода Рунге—Кутта— Фельберга
- Решение краевой задачи с поточно разделёнными краевыми условиями
- Вывод
- Решение систем дифференциальных уравнений методом Рунге-Кутты 4 порядка
- 📹 Видео
Видео:Решение ОДУ методом Рунге-Кутта 4 порядка (программа)Скачать

Ссылки
- http://sadovoya.narod.ru/RK.zip (русский вариант).
- http://sintreseng.narod.ru/RK_Eng.zip (английский, условно-бесплатный вариант)
Видео:6.4 Явные методы Рунге-КуттыСкачать

Оставить комментарий
Видео:3_11. Алгоритм Рунге-КуттыСкачать

Комментарии
Скачала по Вашей ссылке русский вариант, изменила для своей системы диф. уравнений, но при запуске выдаёт ошибку :
Project Ex.exe raised exception class EOverflow with message ‘ Floating point overflow ‘
Помогите, пожалуйста .
Вот изменённый мною модуль:
unit Unit1;
interface
uses
SysUtils, Forms, StdCtrls, Controls, Classes, Dialogs, Math;
type
TForm1 = class(TForm)
Memo1: TMemo;
rk_But: TButton;
procedure rk_ButClick(Sender: TObject);
private
public
end;
var
Form1: TForm1;
pn,k,ro,Pzv: Extended;
implementation
uses rk_method, Windows;
procedure Syst (var t: TFloat; var X: TFloatVector;
var RP: TFloatVector);
const
fdr1=0.503;
fdr2=0.503;
fdr3=0.196;
W1=179.8928;
W2=3773.8568;
W3=2504.1203;
b1=55.9203;
b2=98.6;
b3=98.6;
Ls1=3.78;
Ls2=9;
Ls3=15.3;
Svidj2=1352.438;
Svidj3=1352.438;
my=0.62;
vk=30;
m=1.2;
L1=30.969;
L2=42.131;
delta1=0;
begin
pn:=2.5*Power(10,4);
k:=6*Power(10,-7);
ro:=8.5*Power(10,-7);
Pzv:=3.919*Power(10,7);
RP[0] := (1/(k*W1))*(my*fdr1*sqrt(2/ro)*sqrt(Abs(pn-X[0]))-my*fdr2*sqrt(2/ro)*sqrt(Abs(X[0]-X[1]))-(delta1*delta1*delta1*b1)/(12*ro*vk*Ls1)*X[0]); // dp1/dt
RP[1] := (1/(k*W2))*(my*fdr2*sqrt(2/ro)*sqrt(Abs(X[0]-X[1]))-my*fdr3*sqrt(2/ro)*sqrt(Abs(X[1]-X[2]))-(X[4]*X[4]*X[4]*b2)/(12*ro*vk*Ls2)*X[1]); // dp2/dt
RP[2] := (1/(k*W3))*(my*fdr3*sqrt(2/ro)*sqrt(Abs(X[1]-X[2]))-(X[6]*X[6]*X[6]*b3)/(12*ro*vk*Ls3)*X[2]); // dp3/dt;
RP[3] := (((Svidj2*X[1]*(L1+L2))/L1)-Pzv)*(2/m); // dv2/dt
RP[4] := X[3]; // d delta2/dt
RP[5] := (((Svidj3*X[2]*(L1+L2))/L2)-Pzv)*(2/m); // dv3/dt
RP[6] := X[5]; // d delta3/dt
end;
procedure TForm1.rk_ButClick(Sender: TObject);
var
I, t1, t2: Cardinal;
tOut, InitConds: TFloatVector;
XOuts: TFloatMatrix;
Points: Cardinal;
First, Last: TFloat;
StepsFact: Cardinal;
Count: Word;
begin
Memo1.Clear;
First := 0.0;
Last := 10.0;
Count:= 7;
Points:=10+1; //11 points for output
StepsFact:=1000000; //all steps inside function = 10*StepsFact
try
SetLength(InitConds, Count);
InitConds[0]:=0.0; //x0(0)=0
InitConds[1]:=0.0; //x1(0)=0
InitConds[2]:=0.0; //x2(0)=0
InitConds[3]:=0.0; //x3(0)=0
InitConds[4]:=0.0; //x4(0)=0
InitConds[5]:=0.0; //x5(0)=0
InitConds[6]:=0.0; //x6(0)=0
SetLength(tOut, Points);
SetLength(XOuts, Count, Points);
except
ShowMessage(‘Out of memory. ‘);
exit;
end;
Видео:Численные методы решения ДУ: метод Рунге-КуттаСкачать

Численное решение математических моделей объектов заданных системами дифференциальных уравнений
Введение:
При математическом моделировании ряда технических устройств используются системы дифференциальных нелинейных уравнений. Такие модели используются не только в технике, они находят применение в экономике, химии, биологии, медицине, управлении.
Исследование функционирования таких устройств требуют решения указанных систем уравнений. Поскольку основная часть таких уравнений являются нелинейными и нестационарными, часто невозможно получить их аналитическое решение.
Возникает необходимость использовать численные методы, наиболее известным из которых является метод Рунге — Кутты [1]. Что касается Python, то в публикациях по численным методам, например [2,3], данных по применение Рунге — Кутты крайне мало, а по его модификации — методу Рунге-Кутта-Фельберга вообще нет.
В настоящее время, благодаря простому интерфейсу, наибольшее распространение в Python имеет функцию odeint из модуля scipy.integrate. Вторая функция ode из этого модуля реализует несколько методов, в том числе и упомянутый пятиранговый метод Рунге-Кутта-Фельберга, но, вследствие универсальности, имеет ограниченное быстродействие.
Целью настоящей публикации является сравнительный анализ перечисленных средств численного решения систем дифференциальных уравнений с модифицированным автором под Python методом Рунге-Кутта-Фельберга. В публикации так же приведены решения по краевым задачам для систем дифференциальных уравнений (СДУ).
Краткие теоретические и фактические данные по рассматриваемым методам и программным средствам для численного решения СДУ
Для одного дифференциального уравнения n – го порядка, задача Коши состоит в нахождении функции, удовлетворяющей равенству:
и начальным условиям
Перед решением эта задача должна быть переписана в виде следующей СДУ
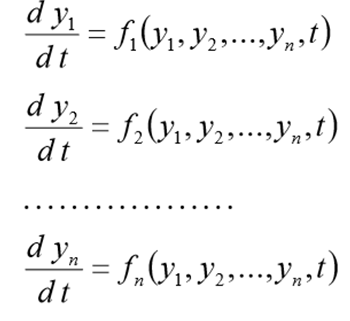
с начальными условиями
Модуль имеет две функции ode() и odeint(), предназначенные для решения систем обыкновенных дифференциальных уравнений (ОДУ) первого порядка с начальными условиями в одной точке (задача Коши). Функция ode() более универсальная, а функция odeint() (ODE integrator) имеет более простой интерфейс и хорошо решает большинство задач.
Функция odeint() имеет три обязательных аргумента и много опций. Она имеет следующий формат odeint(func, y0, t[,args=(), . ]) Аргумент func – это имя Python функции двух переменных, первой из которых является список y=[y1,y2. yn], а второй – имя независимой переменной.
Функция func должна возвращать список из n значений функций 
Второй аргумент y0 функции odeint() является массивом (или списком) начальных значений 
Третий аргумент является массивом моментов времени, в которые вы хотите получить решение задачи. При этом первый элемент этого массива рассматривается как t0.
Функция odeint() возвращает массив размера len(t) x len(y0). Функция odeint() имеет много опций, управляющих ее работой. Опции rtol (относительная погрешность) и atol (абсолютная погрешность) определяют погрешность вычислений ei для каждого значения yi по формуле
Они могут быть векторами или скалярами. По умолчанию
Вторая функция модуля scipy.integrate, которая предназначена для решения дифференциальных уравнений и систем, называется ode(). Она создает объект ОДУ (тип scipy.integrate._ode.ode). Имея ссылку на такой объект, для решения дифференциальных уравнений следует использовать его методы. Аналогично функции odeint(), функция ode(func) предполагает приведение задачи к системе дифференциальных уравнений вида (1) и использовании ее функции правых частей.
Отличие только в том, что функция правых частей func(t,y) первым аргументом принимает независимую переменную, а вторым – список значений искомых функций. Например, следующая последовательность инструкций создает объект ODE, представляющий задачу Коши.
При построении численных алгоритмов будем считать, что решение этой дифференциальной задачи существует, оно единственно и обладает необходимыми свойствами гладкости.
При численном решении задачи Коши
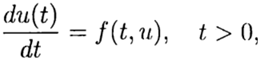

по известному решению в точке t =0 необходимо найти из уравнения (3) решение при других t. При численном решении задачи (2),(3) будем использовать равномерную, для простоты, сетку по переменной t с шагом т > 0.
Приближенное решение задачи (2), (3) в точке 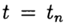

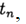


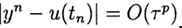

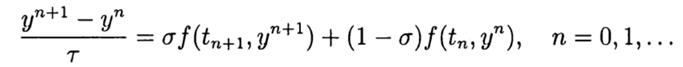
При 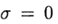
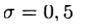
Явные схемы второго и более высокого порядка аппроксимации удобно строить, ориентируясь на метод предиктор-корректор. На этапе предиктора (предсказания) используется явная схема
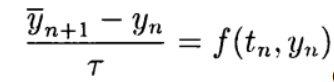
а на этапе корректора (уточнения) — схема
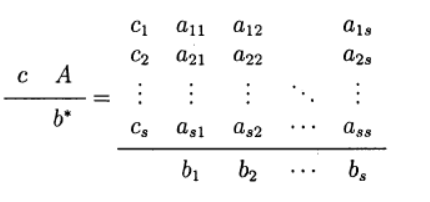
В одношаговых методах Рунге—Кутта идеи предиктора-корректора реализуются наиболее полно. Этот метод записывается в общем виде:

Формула (6) основана на s вычислениях функции f и называется s-стадийной. Если 
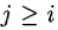

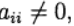

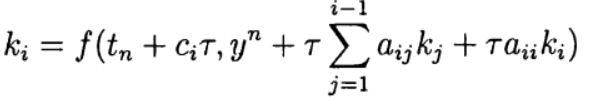
О таком методе Рунге—Кутта говорят как о диагонально-неявном. Параметры 
Одним из наиболее распространенных является явный метод Рунге—Кутта четвертого порядка

Метод Рунге—Кутта— Фельберга
Привожу значение расчётных коэффициентов 
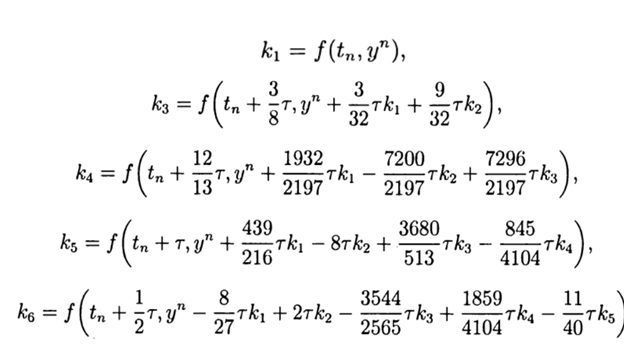
С учётом(9) общее решение имеет вид:
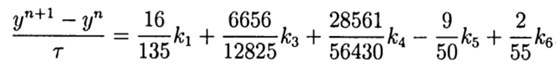
Это решение обеспечивает пятый порядок точности, остаётся его адаптировать к Python.
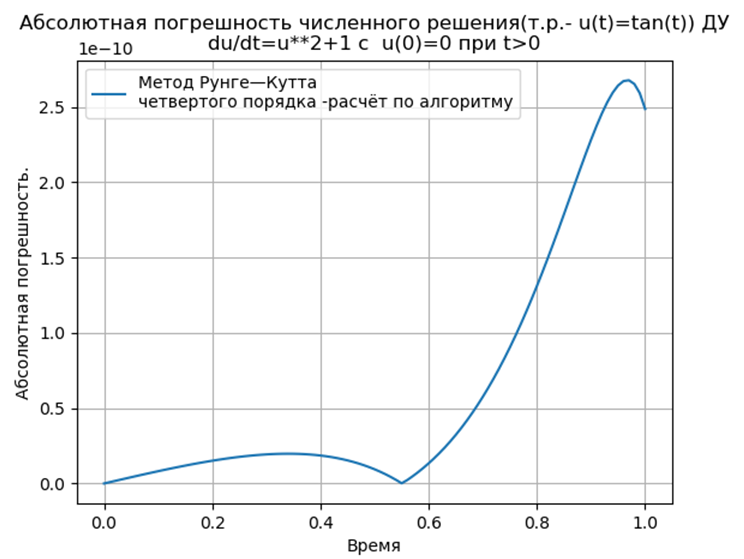
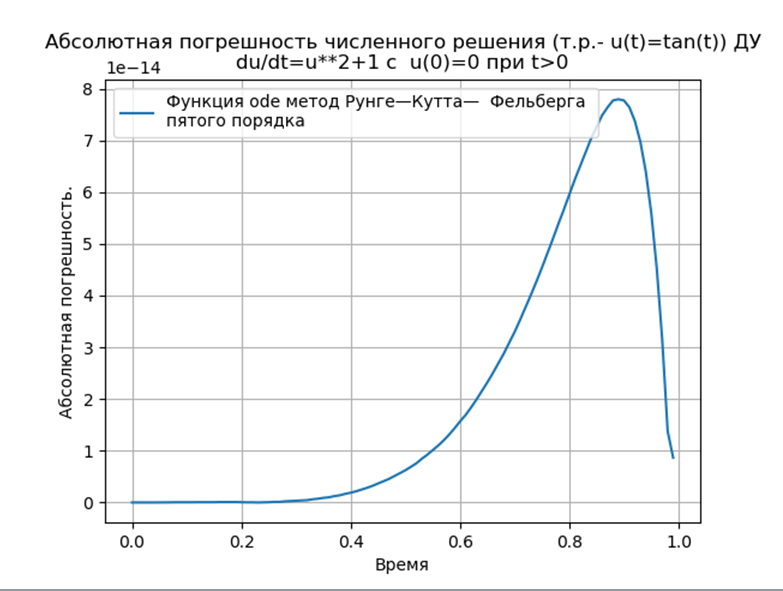
Вычислительный эксперимент по определению абсолютной погрешности численного решения нелинейного дифференциального уравнения  с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
Адаптированные к Python методы Рунге—Кутта и Рунге—Кутта— Фельберга имеют меньшую абсолютную, чем решение с применением функции odeint, но большую, чем с использованием функции edu. Необходимо провести исследование быстродействия.
Численный эксперимент по сравнению быстродействия численного решения СДУ при использовании функции ode с атрибутом dopri5 (метод Рунге – Кутты 5 порядка) и с использованием адаптированного к Python метода Рунге—Кутта— Фельберга
Сравнительный анализ проведём на примере модельной задачи, приведенной в [2]. Чтобы не повторять источник, приведу постановку и решение модельной задачи из [2].
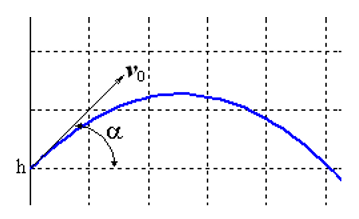
Решим задачу Коши, описывающую движение тела, брошенного с начальной скоростью v0 под углом α к горизонту в предположении, что сопротивление воздуха пропорционально квадрату скорости. В векторной форме уравнение движения имеет вид
где 



Особенность этой задачи состоит в том, что движение заканчивается в заранее неизвестный момент времени, когда тело падает на землю. Если обозначить 
К системе следует добавить начальные условия: 

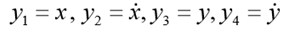
Для модельной задачи положим 
Flight time = 1.2316 Distance = 5.9829 Height =1.8542
Flight time = 1.1016 Distance = 4.3830 Height =1.5088
Flight time = 1.0197 Distance = 3.5265 Height =1.2912
Flight time = 0.9068 Distance = 2.5842 Height =1.0240
Время на модельную задачу: 0.454787
Для реализации средствами Python численного решения СДУ без использования специальных модулей, мною была предложена и исследована следующая функция:
def increment(f, t, y, tau
k1=tau*f(t,y)
k2=tau*f(t+(1/4)*tau,y+(1/4)*k1)
k3 =tau *f(t+(3/8)*tau,y+(3/32)*k1+(9/32)*k2)
k4=tau*f(t+(12/13)*tau,y+(1932/2197)*k1-(7200/2197)*k2+(7296/2197)*k3)
k5=tau*f(t+tau,y+(439/216)*k1-8*k2+(3680/513)*k3 -(845/4104)*k4)
k6=tau*f(t+(1/2)*tau,y-(8/27)*k1+2*k2-(3544/2565)*k3 +(1859/4104)*k4-(11/40)*k5)
return (16/135)*k1+(6656/12825)*k3+(28561/56430)*k4-(9/50)*k5+(2/55)*k6
Функция increment(f, t, y, tau) обеспечивает пятый порядок численного метода решения. Остальные особенности программы можно посмотреть в следующем листинге:
Время на модельную задачу: 0.259927
Предложенная программная реализация модельной задачи без использования специальных модулей имеет почти в двое большее быстродействие, чем с функцией ode, однако нельзя забывать, что ode имеет более высокую точность численного решения и возможности выбора метода решения.
Решение краевой задачи с поточно разделёнными краевыми условиями
Приведем пример некоторой конкретной краевой задачи с поточно разделенными краевыми условиями:
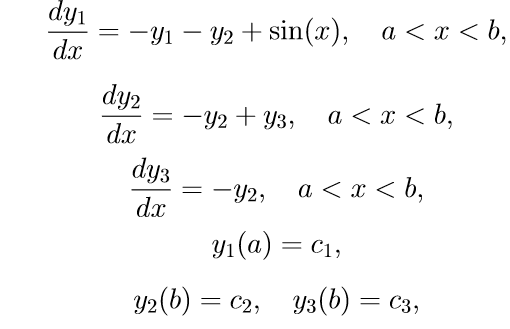
Для решения задачи (11) используем следующий алгоритм:
1. Решаем первые три неоднородные уравнения системы (11) с начальными условиями 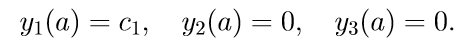
Введем обозначение для решения задачи Коши:
2. Решаем первые три однородные уравнения системы (11) с начальными условиями 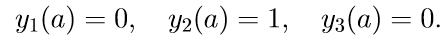
Введем обозначение для решения задачи Коши:
3. Решаем первые три однородные уравнения системы (11) с начальными условиями
Введем обозначение для решения задачи Коши:
4. Общее решение краевой задачи (11) при помощи решений задач Коши записывается в виде линейной комбинации решений: 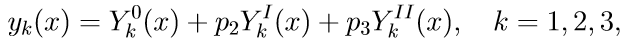
где p2, p3 — некоторые неизвестные параметры.
5. Для определения параметров p2, p3, используем краевые условия последних двух уравнений (11), то есть условия при x = b. Подставляя, получим систему линейных уравнений относительно неизвестных p2, p3:

Решая (12), получим соотношения для p2, p3.
По приведенному алгоритму с применением метода Рунге—Кутта—Фельберга получим следующую программу:
y0[0]= 0.0
y1[0]= 1.0
y2[0]= 0.7156448588231397
y3[0]= 1.324566562303714
y0[N-1]= 0.9900000000000007
y1[N-1]= 0.1747719838716767
y2[N-1]= 0.8
y3[N-1]= 0.5000000000000001
Время на модельную задачу: 0.070878
Вывод
Разработанная мною программа отличается от приведенной в [3] меньшей погрешностью, что подтверждает приведенный в начале статьи сравнительный анализ функции odeint с реализованным на Python метода Рунге—Кутта—Фельберга.
3. Н.М. Полякова, Е.В. Ширяева Python 3. Создание графического интерфейса пользователя (на примере решения методом пристрелки краевой задачи для линейных обыкновенных дифференциальных уравнений). Ростов-на-Дону 2017.
Видео:6.1 Численные методы решения задачи Коши для ОДУСкачать
Решение систем дифференциальных уравнений методом Рунге-Кутты 4 порядка
1. Постановка задачи
3. Выбор метода реализации программы
6. Идентификация переменных
8. Обсуждение результатов
9. Инструкция к программе
Обыкновенные дифференциальные уравнения (ОДУ) широко используются для математического моделирования процессов и явлений в различных областях науки и техники. Переходные процессы в радиотехнике, кинетика химических реакций, динамика биологических популяций, движение космических объектов, модели экономического развития исследуются с помощью ОДУ.
В дифференциальное уравнение n-го порядка в качестве неизвестных величин входят функция y(x) и ее первые n производных по аргументу x
j ( x, y, y 1 , . y (n) )=0. 1.1
Из теории ОДУ известно, что уравнение (1.1) эквивалентно системе n уравнений первого порядка
j k (x, y 1, y 1 ’ ,y 2 ,y 2 ’ , . ,y n ,y n ’ )=0. 1.2
Уравнение (1.1) и эквивалентная ему система (1.2) имеют бесконечное множество решений. Единственные решения выделяют с помощью дополнительных условий, которым должны удовлетворять искомые решения. В зависимости от вида таких условий рассматривают три типа задач, для которых доказано существование и единственность решений.
Первый тип – это задачи Коши, или задачи с начальными условиями. Для таких задач кроме исходного уравнения (1.1) в некоторой точке xo должны быть заданы начальные условия, т.е. значения функции y(x) и ее производных
y(x 0 )=y 0 ’ , y ’ (x 0 )=y 10 , . , y (n-1) (x 0 )=y n-1 , 0 .
Для системы ОДУ типа (1.2) начальные условия задаются в виде
y 1 (x 0 )=y 10 , y 2 (x 0 )=y 20 , . , y n (x 0 )=y n0 . 1.3
Ко второму типу задач относятся так называемые граничные, или краевые задачи, в которых дополнительные условия задаются в виде функциональных соотношений между искомыми решениями. Количество условий должно совпадать с порядком n уравнения или системы. Если решение задачи определяется в интервале x є [ x 0 ,x k] , то такие условия могут быть заданы как на границах, так и внутри интервала. Минимальный порядок ОДУ, для которых может быть сформулирована граничная задача, равен двум.
Третий тип задач для ОДУ – это задачи на собственные значения. Такие задачи отличаются тем, что кроме искомых функций y(x) и их производных в уравнения входят дополнительно m неизвестных параметров l 1, l 2, ј , хm, которые называются собственными значениями. Для единственности решения на интервале [x0, xk] необходимо задать m+n граничных условий. В качестве примера можно назвать задачи определения собственных частот, коэффициентов диссипации, структуры электромагнитных полей и механических напряжений в колебательных системах, задачи нахождения фазовых коэффициентов, коэффициентов затухания, распределения напряженностей полей волновых процессов и т. д.
К численному решению ОДУ приходится обращаться, когда не удается построить аналитическое решение задачи через известные функции. Хотя для некоторых задач численные методы оказываются более эффективными даже при наличии аналитических решений.
Большинство методов решения ОДУ основано на задаче Коши, алгоритмы и программы для которой рассматриваются в дальнейшем.
1. Постановка задачи
Многие процессы химической технологии описываются СДУ — начиная от кинетических исследований и заканчивая химическими технологическими процессами. В основу математических способов описания процессов положены СДУ и СЛАУ. Эти уравнения описывают материальные и тепловые балансы объектов химической технологии, а так же структуры потоков технических веществ в этих аппаратах.
Для получения, распределения технологических параметров во времени и в пространстве (в пределах объекта), необходимо произвести СДУ методом, которых дал бы высокую точность решения при минималььных затратах времени на решение, потому что ЭВМ должна работать в режиме реального времени и успевать за ходом технологического процесса. Если время на решение задачи большое, то управляющее воздействие, выработанное на ЭВМ может привести к отрицательным воздействиям. Методов решения существует очень много. В данной работе будет рассмотрен метод решения СДУ методом Рунге-Кутта 4 порядка.
Для удобства работы на ЭВМ, необходимо данную кинетическую схему преобразовать в удобный для работы на компьютере вид. Для этого необходимо кинетическую схему процесса представить в виде уравнений. При рассмотрении кинетической схемы процесса необходимо учитывать коэффициенты скоростей реакций. Но, так как процесс протекает при изотермических условиях, коэффициенты скоростей реакций можно считать за константы скоростей химической реакции. Из приведенной ниже схемы мы можем составить ряд дифференциальных уравнений, учитывающих изотермичность процесса.
Так как коэффициенты K1,K2,K3,K4 являются константами, то можно уравнение записать в следущем виде.
Для преобразования данных дифференциальных уравнений для использования их в расчетах тепловых и кинетических схем методами Рунге-Кутты необходимо подставлять вместо производных значений концентраций, значения концентраций данных в начале процесса. Это обусловлено тем, что метод Рунге-Кутты четвертого порядка, который будет использован для расчета кинетической схемы процесса. Так как этот метод требует сведений только об одной точке и значений функции.
Разбор и рассмотрение методов, применяемых на практике для решения дифференциальных уравнений, мы начнем с их широкой категории, известной под общим названием методов Рунге-Кутта.
Методы Рунге-Кутта обладают следующими свойствами:
1. Эти методы являются одноступенчатыми: чтобы найти у m+1, нужна
информация о предыдущей точке xm, ym.
2. Они согласуются с рядом Тейлора вплоть до членов порядка hp, где степень р
различна для различных методов и называется порядковым номером или
3. Они не требуют вычисления производных от f (x, y), а требуют вычисления
Рассмотрим сначала геометрическое построение и выведем некоторые формулы на основе геометрических аналогий. После этого мы подтвердим полученные результаты аналитически.
Предположим, нам известна точка xm, ym на искомой кривой. Тогда мы можем провести прямую линию с тангенсом угла наклона уў m =f(x m, y m ), которая пройдет через точку x m, y m. Это построение показано на рис. 1, где кривая представляет собой точное, но конечно неизвестное решение уравнения, а прямая линия L1 построена так, как это только что описано.
Тогда следующей точкой решения можно считать ту, где прямая L 1 пересечет ординату, проведенную через точку x=x m+1 =x m +h.
Уравнение прямой L 1 выглядит так: y=y m +yў m (x-x m ) так как yў =f(x m, y m ) и кроме того, x m+1 =x m +h тогда уравнение примет вид
y m+1 =y m +h*f(x m, y m ) 1. 1
Ошибка при x=x m+1 показана в виде отрезка е. Очевидно, найденное таким образом приближенное значение согласуется с разложением в ряд Тейлора вплоть до членов порядка h, так что ошибка ограничения равна e t =Кh2
Заметим, что хотя точка на графике 1 была показана на кривой, в действительности y m является приближенным значением и не лежит точно на кривой.
Формула 1. 1 описывает метод Эйлера, один из самых старых и широко известных методов численного интегрирования дифференциальных уравнений. Отметим, что метод Эйлера является одним из методов Рунге-Кутта первого порядка.
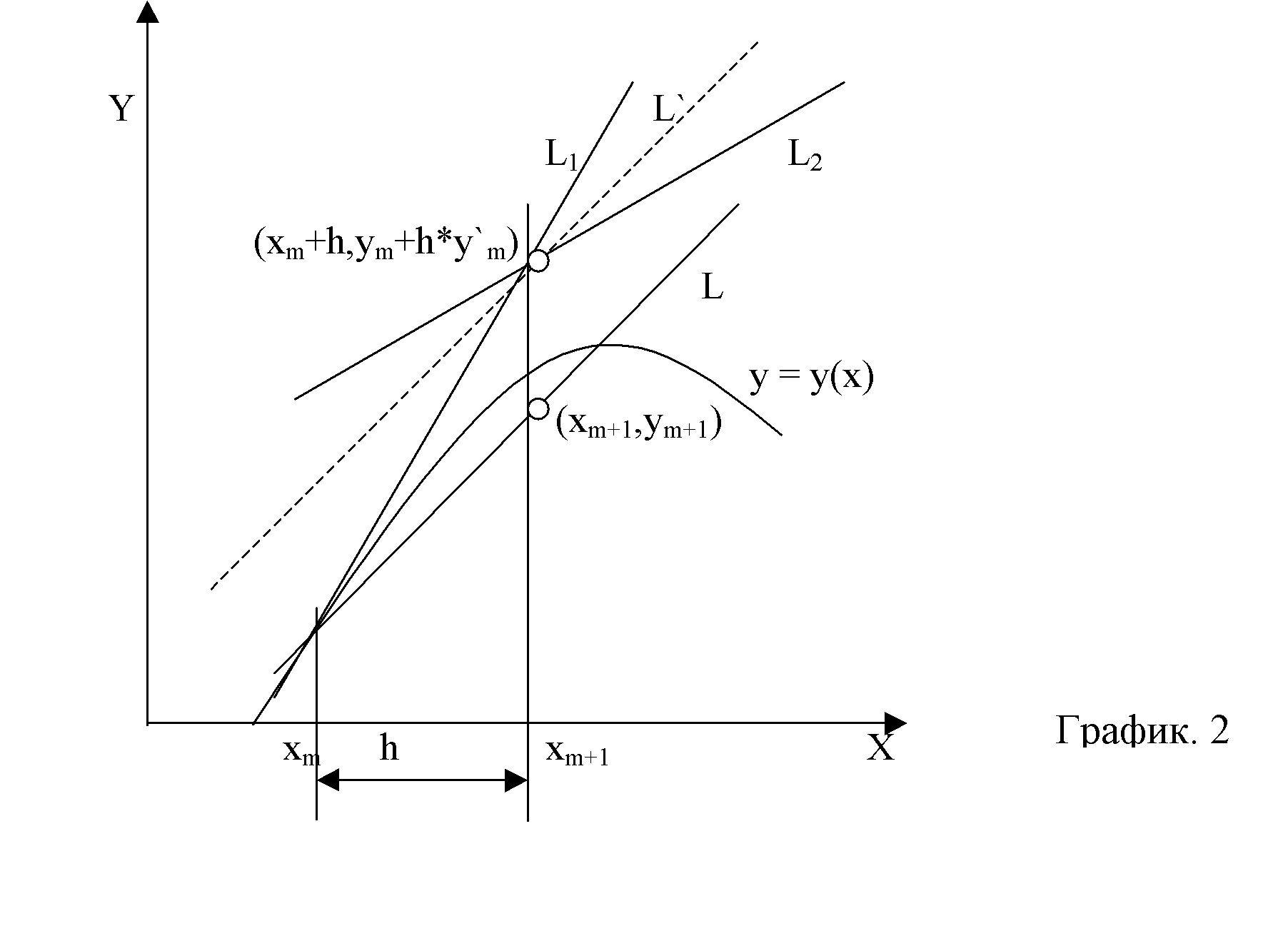
Рассмотрим исправленный метод Эйлера и модификационный метод Эйлера. В исправленном методе Эйлера мы находим средний тангенс угла наклона касательной для двух точек: x m, y m и x m +h, y m +hyў m. Последняя точка есть та самая, которая в методе Эйлера обозначалась x m+1, y m+1. Геометрический процесс нахождения точки x m+1, y m+1 можно проследить по рис. 2. С помощью метода Эйлера находится точка x m +h, y m +hyў m, лежащая на прямой L 1. В этой точке снова вычисляется тангенс, дает прямую L . Наконец, через точку x m, y m мы проводим прямую L, параллельную L . Точка, в которой прямая L пересечется с ординатой, восстановленной из x=x m+1 =x m +h, и будет искомой точкой x m+1, y m+1.
Тангенс угла наклона прямой L и прямой L равен
Ф(x m, y m, h)=Ѕ [f(x m, y m )+f(x m +h, y m +yў m h)] 1. 2
где yў m =f(x m, y m ) 1. 3
Уравнение линии L при этом записывается в виде
y=y m +(x-x m )Ф(x m, y m, h),
y m+1 =y m +hФ(x m, y m, h). 1. 4
Соотношения 1. 2, 1. 3, 1. 4 описывают исправленный метод Эйлера.
f(x, y)=f(x m, y m )+(x-x m )¶ f/¶ x+(y-y m )¶ f/¶ x+ј 1. 5
где частные производные вычисляются при x=x m и y=y m.
Подставляя в формулу 1. 5 x=x m +h и y=y m +hyў m и используя выражение 1. 3 для yў m, получаем
f(x m +h, y m +hyў m )=f+hf x +hff y +O(h2),
где снова функция f и ее производные вычисляются в точке x m, y m. Подставляя результат в 1. 2 и производя необходимые преобразования, получаем
Ф(x m, y m, h)=f+h/2(f x +ff y )+O(h2).
Подставим полученное выражение в 1. 4 и сравним с рядом Тейлора
y m+1 =y m +hf+h2/2(f x +ff y )+O(h3).
Как видим, исправленный метод Эйлера согласуется с разложением в ряд Тейлора вплоть до членов степени h2, являясь, таким образом, методом Рунге-Кутты второго порядка.
Рассмотрим модификационный метод Эйлера. Рассмотрим рис. 3 где первоначальное построение сделано так же, как и на рис. 2. Но на этот раз мы берем точку, лежащую на пересечении этой прямой и ординатой x=x+h/2. На рисунке эта точка образована через Р, а ее ордината равна y=y m +(h/2)yў m. Вычислим тангенс угла наклона касательной в этой точке
Ф(x m, y m, h)=f+(x m +h/2, y m +h/2*yў m ), 1. 6
где yў m =f(x m, y m ) 1. 7
Прямая с таким наклоном, проходящая через Р, обозначена через L *. Вслед за тем, мы проводим через точку xm, ym прямую параллельную L *, и обозначаем ее через L 0. Пересечение этой прямой с ординатой x=x m +h и даст искомую точку x m+1, y m+1. Уравнение прямой можно записать в виде y=y m +(x-x m )Ф(x m, y m, h),
где Ф задается формулой 1. 6. Поэтому
y m+1 =y m +hФ(x m, y m, h) 1. 8
Соотношения 1. 6, 1. 7, 1. 8 описывают так называемый модификационный метод Эйлера и является еще одним методом Рунге-Кутта второго порядка. Обобщим оба метода. Заметим, что оба метода описываются формулами вида
y m+1 =y m +hФ(x m, y m, h) 1. 9
и в обоих случаях Ф имеет вид
Ф(x m, y m, h)=a 1 f(x m, y m )+a 2 f(x m +b 1 h, y m +b 2 hyў m ), 1. 10
где yў m =f(x m, y m ) 1. 11
В частности, для исправленного метода Эйлера
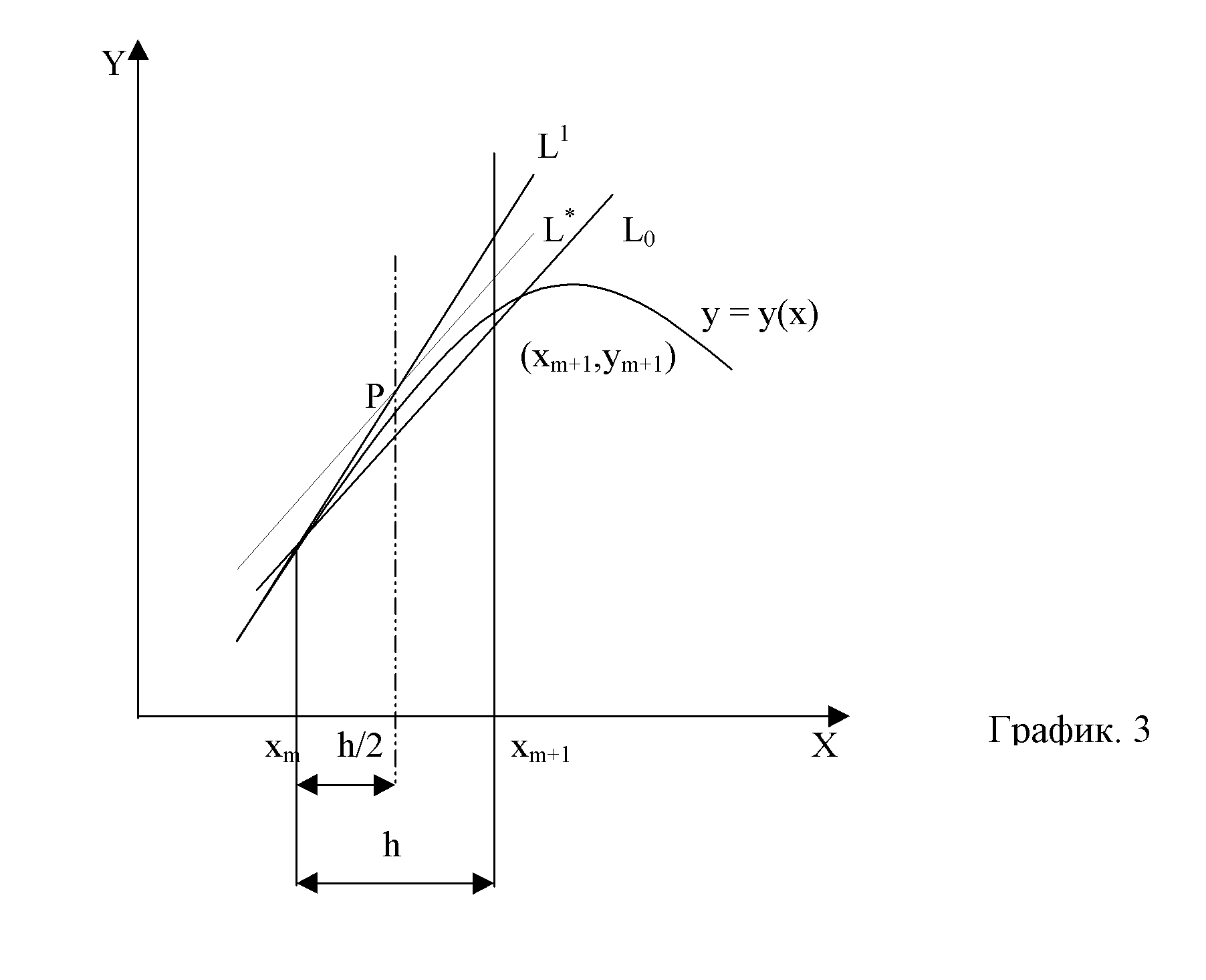
Формулы 1. 9, 1. 10, 1. 11 описывают некоторый метод типа Рунге-Кутты. Посмотрим, какого порядка метод можно рассчитывать получить в лучшем случае и каковы допустимые значения параметров a 1, a 2, b 1 и b 2 .
Чтобы получить соответствие ряду Тейлора вплоть до членов степени h, в общем случае достаточно одного параметра. Чтобы получить согласование вплоть до членов степени h2, потребуется еще два параметра, так как необходимо учитывать члены h2f x и h2ff y. Так как у нас имеется всего четыре параметра, три из которых потребуются для создания согласования с рядом Тейлора вплоть до членов порядка h2, то самое лучшее, на что здесь можно рассчитывать — это метод второго порядка.
В разложении f(x, y) в ряд 1. 5 в окрестности точки x m, y m положим x=x m +b 1 h,
Тогда f(x m +b 1 h, y m +b 2 hf)=f+b 1 hf x +b 2 hff y +O(h2), где функция и производные в правой части равенства вычислены в точке x m, y m.
Тогда 1. 9 можно переписать в виде y m+1 =y m +h[a 1 f+a 2 f+h(a 2 b 1 f x +a 2 b 2 ff y )]+O(h3).
Сравнив эту формулу с разложением в ряд Тейлора, можно переписать в виде
y m+1 =y m +h[a 1 f+a 2 f+h(a 2 b 1 f x +a 2 b 2 ff y )]+O(h3).
Если потребовать совпадения членов hf, то a 1 +a 2 =1.
Сравнивая члены, содержащие h2f x, получаем a 2 b 1 =1/2.
Сравнивая члены, содержащие h2ff y, получаем a 2 b 2 =1/2.
Так как мы пришли к трем уравнениям для определения четырех неизвестных, то одно из этих неизвестных можно задать произвольно, исключая, может быть, нуль, в зависимости от того, какой параметр взять в качестве произвольного.
Положим, например, a 2 =w № 0. тогда a 1 =1-w , b 1 =b 2 =1/2w и соотношения 1. 9, 1. 10, 1. 11 сведутся к
y m+1 =y m +h[(1-w )f(x m, y m )+w f(x m +h/2w , y m +h/2w f(x m, y m ))]+O(h3) 1. 12
Это наиболее общая форма записи метода Рунге-Кутта второго порядка. При w =1/2 мы получаем исправленный метод Эйлера, при w =1 получаем модификационный метод Эйлера. Для всех w , отличных от нуля, ошибка ограничения равна
Методы Рунге-Кутта третьего и четвертого порядков можно вывести совершенно аналогично тому, как это делалось при выводе методов первого и второго порядков. Мы не будем воспроизводить выкладки, а ограничимся тем, что приведем формулы, описывающие метод четвертого порядка, один из самых употребляемых методов интегрирования дифференциальных уравнений. Этот классический метод Рунге-Кутта описывается системой следующих пяти соотношений
y m+1 =y m +h/6(R 1 +2R 2 +2R 3 +R 4 ) 1. 14
где R 1 =f(x m, y m ), 1. 15
R 2 =f(x m +h/2, y m +hR 1 /2), 1. 16
R 3 =f(x m +h/2, y m +hR 2 /2), 1. 17
R 4 =f(x m +h/2, y m +hR 3 /2). 1. 18
Ошибка ограничения для этого метода равна e t =kh5
так что формулы 1. 14-1. 18 описывают метод четвертого порядка. Заметим, что при использовании этого метода функцию необходимо вычислять четыре раза.
3. Выбор метода реализации программы
Исходя из вышеизложенного, для решения систем дифференциальных уравнений мы выбираем наиболее точный метод решения – метод Рунге-Кутта 4 порядка, один из самых употребляемых методов интегрирования дифференциальных уравнений.
- этот метод является одноступенчатым и одношаговым
- требует информацию только об одной точке
- имеет небольшую погрешность
- значение функции рассчитывается при каждом шаге
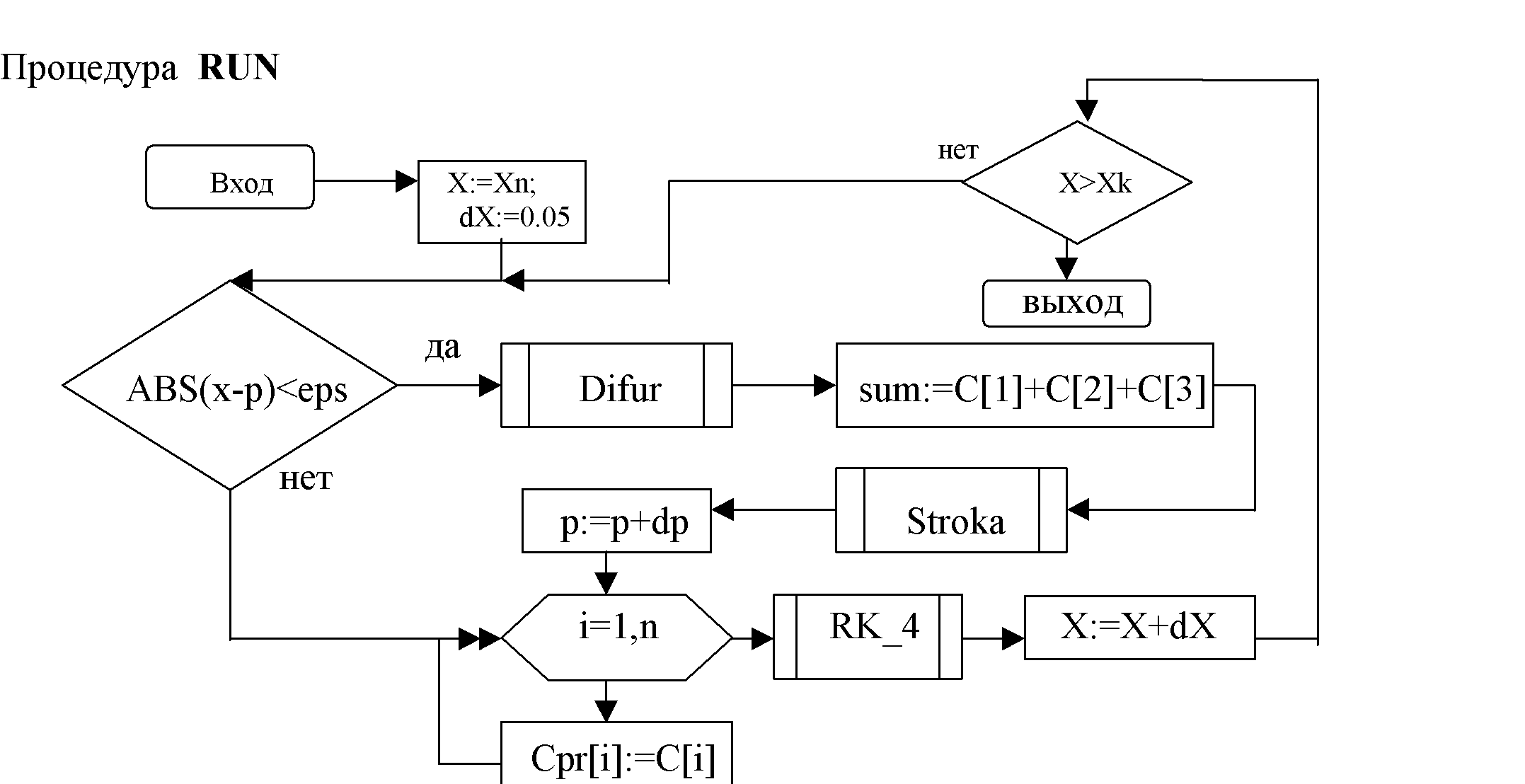
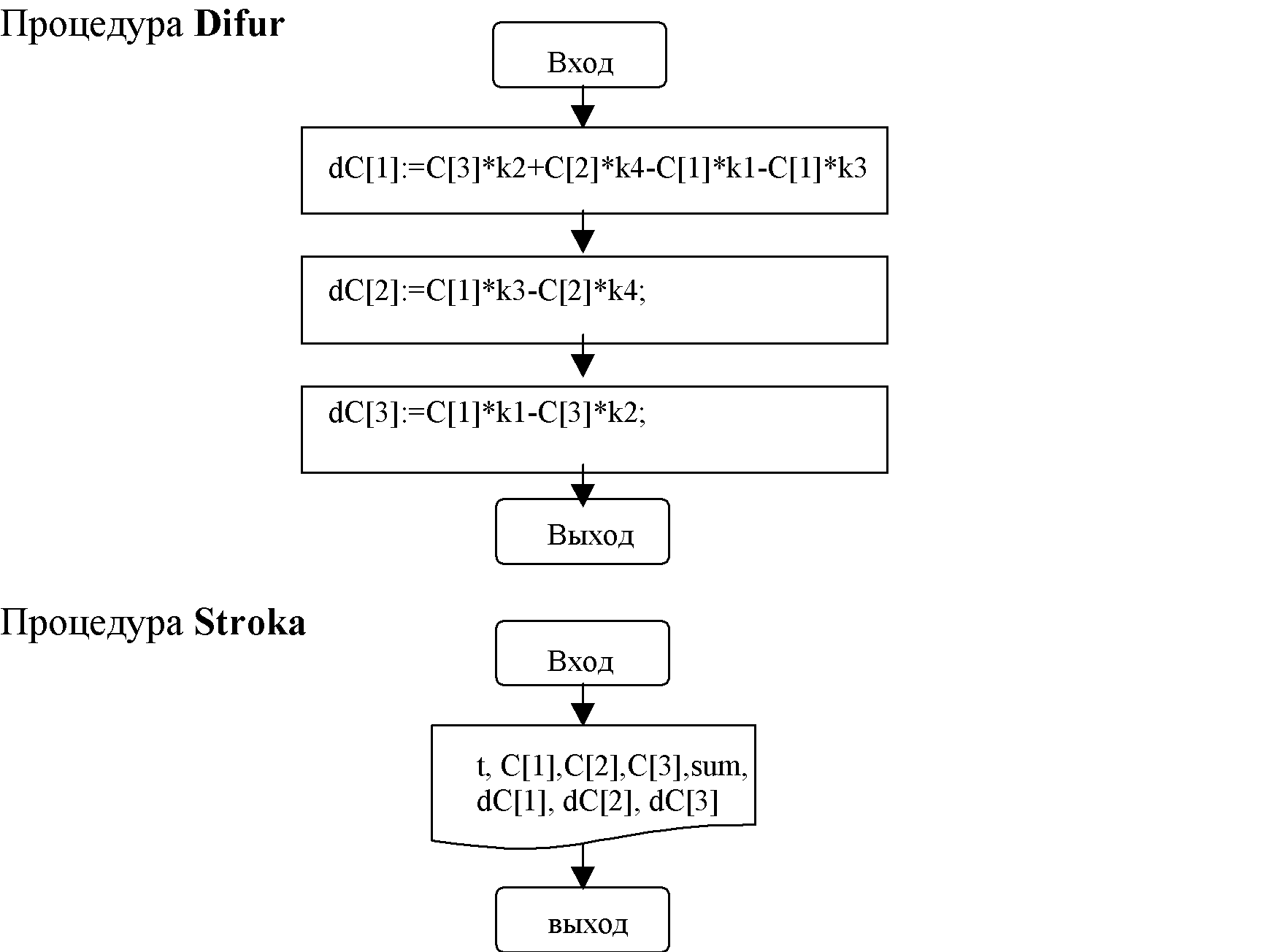
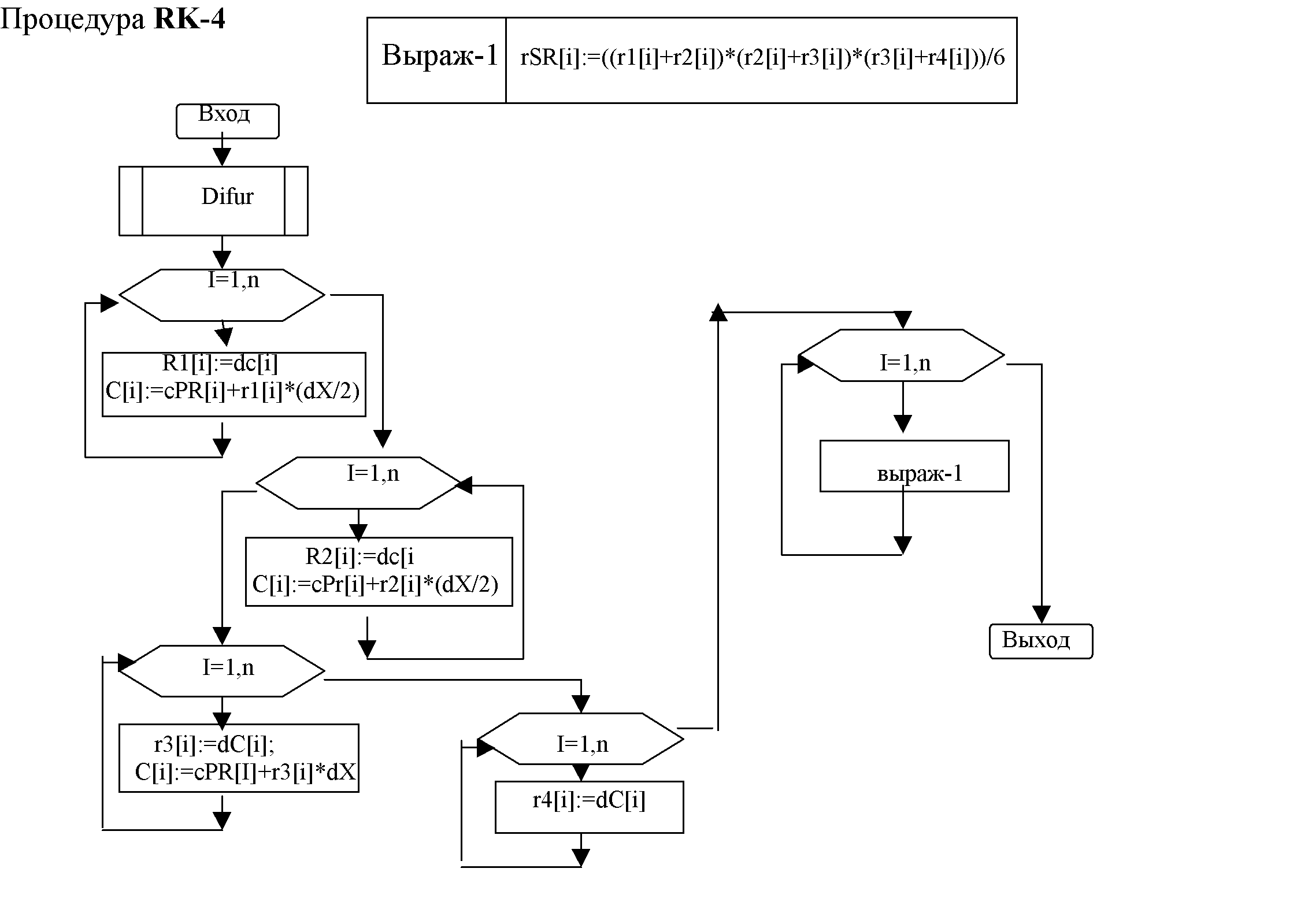
4. Блок-схема программмы
PROGRAM smith_04;USES crt; VAR i,n:integer; sum,k1,k2,k3,k4,p,dp,eps,Xn,Xk,X,dX:real; rSR,C,dC,r1,r2,r3,r4,cPR:array[1..3] of real;
📹 Видео
Программируем метод Рунге-Кутта 4 порядкаСкачать

04 Метод Рунге-Кутты 4-го порядкаСкачать

Решение ОДУ: метод Рунге КуттаСкачать

Метод ЭйлераСкачать

Решение системы дифференциальных уравнений методом ЭйлераСкачать

4a. Методы Рунге-КуттаСкачать

Интегрирование систем дифференциальных уравнений методом Рунге-Кутта 4-ог порядка в Arduino IDE.Скачать

Метод Рунге Кутты 2 и 4 порядковСкачать

ОДУ. 4 Системы дифференциальных уравненийСкачать

Видеоурок "Системы дифференциальных уравнений"Скачать

Решение ОДУ методом Рунге КуттаСкачать

Численные методы. Лекция 10: метод Эйлера, методы Рунге-КуттыСкачать

Методы численного анализа - Метод Рунге-Кутта для ОДУ 2 порядкаСкачать

Метод Эйлера. Метод Рунге-Кутта. Классический метод Рунге-Кутта 4 порядка точности. Лекция №9Скачать

Решение системы ОДУ в PythonСкачать








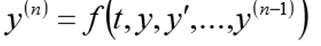
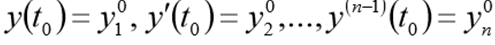


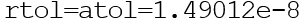
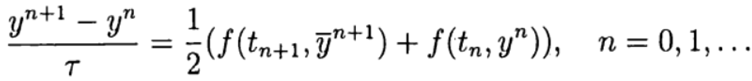
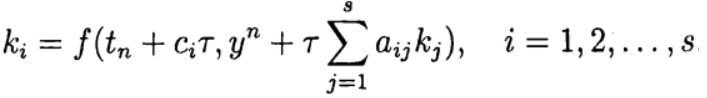
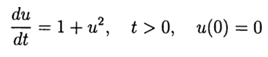 с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга