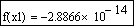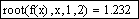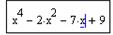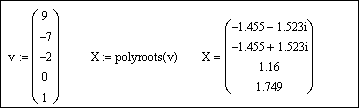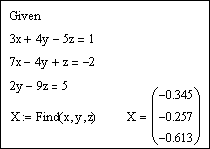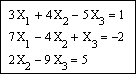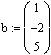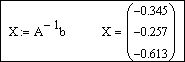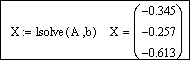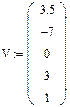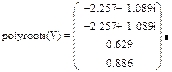Метод root для решения уравнений (3 видео)

Метод root для решения уравнений

Глава 4. Решение уравнений

4.1 Функция root

Функция root используется для решения одного уравнения с одним неизвестным. Перед началом решения желательно построить график функции, чтобы проверить, есть ли корни, то есть пересекает ли график ось абсцисс. Начальное приближение лучше всего выбрать по графику поближе к корню, так как итерационные методы весьма чувствительны к выбору начального приближения.

Обращение к функции осуществляется следующим образом:

root ( f ( x ), x ), где f ( x ) – выражение, равное нулю; x – аргумент, варьируя который, система ищет значение, обращающее в нуль ( рис. 4.1 ).

Уравнение

начальное приближение

решение

или

другие корни

Задан интервал поиска корней

Рис. 4. 1 Использование функции root

Функция f ( x ) и аргумент x должны быть скалярами, то есть результат вычисления функции – число, а не вектор или матрица. Функция root использует метод секущих. Корень уравнения – ближайшее к начальному приближению значение x , обращающее функцию f ( x ) в нуль. Если корней несколько, то для отыскания каждого корня необходимо задавать свое начальное приближение.

Mathcad позволяет вместо начального приближения задавать диапазон значений аргумента, в котором лежит значение искомого корня. В этом случае обращение к функции root должно иметь четыре параметра:

root ( f ( x ), x , а, b ),

где a и b – границы интервала, в котором лежит один корень уравнения. Внутри интервала не должно быть больше одного корня, так как Mathcad выводит на экран лишь один корень, лежащий внутри интервала.

Значение функции на границах интервала должно быть разного знака, иначе, возможно, корень не будет найден.

Если уравнение не имеет действительных корней, то есть на графике функция f ( x ) нигде не равна нулю, то для вывода комплексных корней надо ввести начальное приближение в комплексной форме (рис. 4.2) .

Если функция имеет мнимый корень,

то начальное приближение задается комплексным числом

— начальное приближение

Рис. 4. 2 Решение уравнения с комплексными корнями

Для ввода мнимой единицы надо ввести с клавиатуры 1 i или 1 j .

Если уравнение имеет несколько корней, то для их нахождения можно использовать разложение функции f ( x ) на простые множители:

где x _1, x ₂ , , x_n – корни уравнения. Начальное приближение можно задать только для первого корня. В качестве функции f ( x ) нужно взять

где ,

и т. д. (рис. 4.3)

у этой функции 3 корня

диапазон значений х для вывода графика

Рис. 4. 3 Определение трех корней уравнения

Если функция f ( x ) имеет малый наклон вблизи искомого корня, то функция root ( f ( x ), x ) может сходиться к значению, довольно далеко отстоящему от корня. В таком случае для уточнения корня необходимо уменьшить значение погрешности вычислений, задаваемое встроенной переменной TOL . Для этого:

1) в стандартном меню Mathcad выберите команду Tools → Worksheet Options → Built – In Variables (Инструменты → Параметры документов → Встроенные переменные);

2) в открывшемся окне поменяйте значение Convergence Tolerance ( TOL ) (Погрешность сходимости).

Чем меньше константа TOL , тем ближе к нулю будет значение функции при найденном корне уравнения, но тем больше будет время вычисления корня.

Для повышения точности расчета корня можно заменить f ( x ) на

Корень можно найти и по графику, увеличив масштаб. Для этого необходимо:

1) выделить график, щелкнув левой кнопкой мыши внутри графика;

2)в главном меню Mathcad выбрать команду Format → Graph → Zoom (Формат→График→Масштаб);

3) при нажатии левой кнопки мыши обвести пунктирной линией область графика вблизи искомого корня, которую надо увеличить;

4) в открытом окне X – Y Zoom (Масштаб по осям X – Y ) нажать кнопку Zoom .

Прямо с графика можно передать в буфер обмена численное значение корня. Для этого выполните следующие действия:

1) Выделите график, щелкнув левой кнопкой мыши внутри графика,

2) в главном меню Mathcad выберите команду Format → Graph → Trace (Формат→График→Трассировка),

3) щелкните левой кнопкой мыши внутри графика – появится перекрестье осей,

4) двигая мышь при нажатой левой кнопке, установите перекрестье на пересечении графика с осью абсцисс. При этом численные значения координат перекрестья появляются в открытом окне X – Y Trace (Трассировка X и Y ).

5) правильно выбрав положение перекрестья, нажмите кнопки Copy X и Copy Y – численные значения будут помещены в буфер

6) вне поля графика запишите имя, которое хотите дать корню, и оператор присваивания :=. Нажмите кнопку Paste (Вставить) в стандартном меню Mathcad или в контекстном меню, открывающемся при нажатии правой кнопки мыши.

Рис. 4. 4 Определение корня уравнения по графику

В окне X – Y Trace есть пункт Track Data Points (Отмечать расчетные точки). Если установить этот флажок, при перемещении мыши пунктирное перекрестье на графике будет перемещаться скачками, отмечая расчетные значения функции. Если флажок снять, движение перекрестья становится плавным.

При работе с Mathcad постоянно пользуйтесь правой кнопкой мыши (в контекстном меню каждый раз появляются новые, наиболее нужные в данный момент функции). Щелкните правой кнопкой мыши на графике: в открывшемся контекстном меню есть пункты Zoom и Trace .

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Метод root для решения уравнений

РЕШЕНИЕ УРАВНЕНИЙ И СИСТЕМ УРАВНЕНИЙ

4 Решение уравнений и систем средствами Mathcad

Система Mathcad обладает широкими возможностями численного решения уравнений и систем уравнений.

Функция root, блоки Given…Find, Given…Minerr

В ходе численного решения обычно выделяют два этапа:

отделение корней – определение интервала нахождения каждого корня или определение приблизительного значения корня. В системе Mathcad наиболее наглядным будет отделение корней уравнения графическим способом;
уточнение корней – нахождение численного значения корня с указанной точностью.

Точность нахождения корня устанавливается с помощью системной переменной TOL (Convergence Tolerance – Допуск сходимости), которая по умолчанию равна 10 -3 . Чем меньше значение TOL, тем точнее, вообще говоря, находится корень уравнения. Однако оптимальным является TOL = 10 -5 . Переопределить значение TOL можно в окне математических свойств документа Math Options на вкладке Build-In Variables (Встроенные переменные) или присваиванием, например, TOL:=0.0001.

Для решения одного уравнения с одной неизвестной предназначена встроенная функция root, которая в общем виде задается

root(f(x), x, [a, b])

и возвращает значение переменной x, при котором функция f(x) обращается в ноль. Аргументы функции root:

f(x) – функция левой части уравнения f(x) = 0;
x – переменная, относительно которой требуется решить уравнение;
a, b (необязательные) – действительные числа, такие что a -1 слева: A -1 Ax=A -1 b. Учитывая, что A -1 A, вектор-столбец решений системы можно искать в виде

Этот прием используется в Mathcad так:

задается матрица коэффициентов при неизвестных системы A;
задается столбец свободных членов b;
вводится формула для нахождения решения системы X:=A -1 b;
выводится вектор решений системы X=.

Кроме того, пакет Mathcad имеет встроенную функцию

lsolve(A, b),

возвращающую вектор-столбец решений системы линейных алгебраических уравнений. Аргументами функции lsolve являются матрица коэффициентов при неизвестных системы и столбец свободных членов. Порядок решения аналогичен рассмотренному, но вместо формулы X:=A -1 b используется X:=lsolve(A, b).

Реализовать широко известный метод Гаусса решения систем линейных уравнений позволяет встроенная функция rref(M), возвращающая ступенчатый вид матрицы M. Если в качестве аргумента взять расширенную матрицу системы, то в результате применения rref получится матрица, на диагонали которой – единицы, а последний столбец представляет собой столбец решений системы.

Решение системы линейных уравнений можно осуществить с помощью блоков Given…Find, Given…Minerr. При этом неизвестным системы задается произвольное начальное приближение, а проверка необязательна.

Порядок выполнения лабораторной работы

Загрузить Mathcad Start / All Programs / Mathsoft Apps / Mathcad (Пуск / Все программы / Mathsoft Apps / Mathcad).
Сохранить в личной папке на диске z: новый документ с именем ФИО1, лучше использовать латинские буквы. Производить сохранение регулярно в процессе работы (Ctrl + S).
Вставить текстовую область Insert / Text Region (Вставка / Область текста) и ввести в поле документа текст:

Лабораторная работа № 4
Решение уравнений и систем в Mathcad.

В новой текстовой области ввести фамилию, имя, отчество, учебный шифр и номер варианта.
Выполнить задание 1.

Задание 1. Решить уравнение .

Решение.

Решение данного уравнения будем проводить в два этапа: отделение корней уравнения графически, уточнение корней уравнения.

Определим функцию f(x), равную левой части данного уравнения, когда правая равна нулю:

Зададим ранжированную переменную x на некотором диапазоне с мелким шагом, например:

Вставим в документ графическую область. Для этого выберем дважды пиктограмму с изображением графика сначала на панели Math (Математика), затем на палитре графиков Graph или выполним из главного меню последовательность команд Insert / Graph / X-Y Plot (Вставка / График / X-Y Зависимость).

Снизу по оси абсцисс наберем x, а сбоку по оси ординат введем f(x).

Для появления графика щелкнем левой клавишей мыши вне графической области.

Отформатируем график функции f(x). Для этого щелкнем правой клавишей мыши в области графика и выберем в контекстном меню команду Format (Формат). Установим пересечение осей графика (Crossed – Только оси), добавим вспомогательные линии по координатным осям (Grid Lines – Вспомогательные линии). Отменим при этом автосетку (Autogrid – Автосетка) и установим количество линий сетки, равное 10.

Для подтверждения внесенных изменений нажмем последовательно кнопки Apply (Применить) и ОК.

После указанных преобразований график функции f(x) будет выглядеть следующим образом:

Из графика функции f(x) видно, что уравнение имеет три корня, которые приблизительно равны: x1 ≈ -1; x2 ≈ 1; x3 ≈ 2,5.

Этап отделения корней завершен.

Уточним теперь корни уравнения с помощью функции root.

Присвоим начальное приближение переменной x и укажем точность поиска корня:

Уточним заданное приближение к значению корня с помощью функции root:

Выполним проверку, подтверждающую, что первый корень найден с заявленной точностью:

Начальное приближение можно не задавать при использовании в качестве аргументов root границ отрезка нахождения корня, например, второй корень можно уточнить:

Задание 2. Решить уравнение .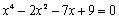

Решение.

Напечатаем левую часть уравнения, не приравнивая выражение к 0, и выделим синим курсором переменную x:

Выберем из главного меню Symbolics / Polynomial Coefficients (Символика / Коэффициенты полинома). Появившийся вектор коэффициентов полинома выделим целиком синим курсором и вырежем в буфер обмена, используя кнопку Вырезать на панели инструментов Formatting (Форматирование) или комбинацию клавиш Ctrl + X.

Напечатаем v := и вставим вектор из буфера обмена, используя кнопку Вставить на панели инструментов или комбинацию клавиш Ctrl + V.

Для получения результата напечатаем polyroots(v) =:

Задание 3. Решить систему линейных уравнений 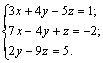Сделать проверку.

Решение.

1-й способ. Использование блока Given … Find.

Зададим всем неизвестным, входящим в систему уравнений, произвольные начальные приближения, например:

Напечатаем слово Given. Установим визир ниже и наберем уравнения системы, каждое в своем блоке. Используем при этом логический знак равенства (Ctrl + =).

После ввода уравнений системы напечатаем X := Find(x, y, z) и получим решение системы в виде вектора, состоящего из трех элементов:

Сделаем проверку, подставив полученные значения неизвестных в уравнения системы, например, следующим образом

После набора знака «=» в каждой строке должен быть получен результат, равный или приблизительно равный правой части системы. В данном примере системная переменная ORIGIN = 1.

2-й способ. Использование блока Given…Minerr.

Порядок решения системы этим способом аналогичен порядку использования блока Given … Find и представлен ниже вместе с проверкой:

3-й способ. Решение системы линейных уравнений матричным способом.

Создадим матрицу А, состоящую из коэффициентов при неизвестных системы. Для этого напечатаем A := , вызовем окно создания массивов (Ctrl + M). Число строк (Rows) и столбцов (Columns) матрицы данной системы равно 3. Заполним пустые места шаблона матрицы коэффициентами при неизвестных системы, как показано ниже:

Зададим вектор b свободных членов системы. Сначала напечатаем b :=, затем вставим шаблон матрицы(Ctrl + M), где количество строк (Rows) равно 3, а количество столбцов (Columns) равно 1. Заполним его:

Решим систему матричным способом по формуле

Решим систему с помощью функции lsolve:

Для проверки правильности решения системы, полученного матричным способом, достаточно вычислить произведение A·X, которое должно совпасть с вектором-столбцом свободных членов b:

Видео:Числовое решение. Функция root в MathCAD 14 (28/34)Скачать

Решение уравнений с помощью функции root

Дата добавления: 2015-07-23 ; просмотров: 6606 ; Нарушение авторских прав

Функция root осуществляет решение алгебраических и трансцендентных уравнений, определяя вещественные корни уравнений. MathCAD в функции root использует для поиска корня метод секущих.

· f(x) – решаемое уравнений f(x);

· x – аргумент функции f(x) (искомое неизвестное уравнения).

При использовании функции rootзадаётся начальное приближение корня x0.

Функция root представляется в одной из следующих форм:

1-ый вариант 2-ой вариант 3-ий вариант

x:=x0	x:=x0	x:=x0
Root (f(x),x)=	z=root (f(x),x)	j(x):=f(x)
z=	z:=root(j(x),x)
z=

Если после многих итераций MathCAD не может найти решение, то появляется сообщение: «отсутствует сходимость». Эта ошибка может быть вызвана следующими причинами:

уравнение не имеет корней;
корни уравнения расположены далеко от начального приближения;
функция f(x) имеет локальные экстремумы между начальным приближением и корнем;
функция f(x) имеет разрывы между начальным приближением и корнем;
функция f(x) имеет комплексный корень, но начальное приближение было вещественным.

Чтобы установить причину ошибки рекомендуется построить график функции f(x). Он поможет выяснить наличие корней уравнения, определить начальные приближения.

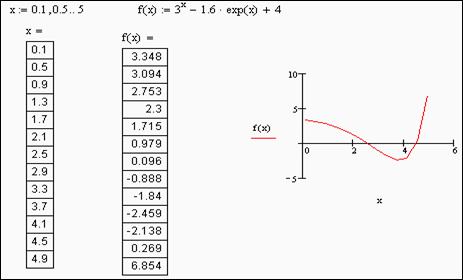
Пример 4.1. Решить уравнение: 3 X — 1.6*e X + 4=0.

Технология выполнения задания.

Определим количество корней уравнения и их интервалы изоляции. Для этого:

задаём ранжированную переменную x=0.1,0.5..5 (примерный диапазон изменения) и заданное уравнение без правой его части (=0).
Набираем x= (на экране появляется диапазон изменения x;)
Набираем f(x)= (на экране появляется диапазон изменения заданного уравнения).
В системе MathCAD выполнить команды View®Toolbars ® Graph. На появившейся панели Graph щёлкнуть по кнопке XY – Plot.
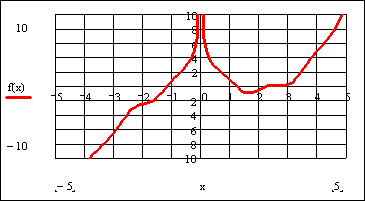
Построить график заданного уравнения (см. рис. ).
Определить по графику интервалы изоляции корней.

Построение графика заданного уравнения представлено на рис.4.1.

Рис. 4.1. График уравнения 3 Х – 1,6e X +4

По графику интервалы изоляции корней x₁ и x₂ соответственно равны: 2.5 Х – 1.6exp(x)+4,x)=2.541

root(3 Х – 1.6exp(x)+4,x)=4.473

Рис. 4.2. Решение уравнения 3 Х – 1,6*e X +4

Проверить правильность определения корней, подставив полученные решения в исходное уравнение.

Решение уравнений с помощью функции

ФункцияFindпредназначенадля решениясистемуравнений методом итераций. Как частный случай, функция может определять корни одного уравнения.

Решение уравнения выполняется в следующей последовательности:

задать начальное приближение корня х₀ из области его изоляции;
написать слово Given, указывающее на то, что далее следует заданное уравнение;
написать заданное уравнение. Следует иметь в виду, что при вводе в уравнение знака равенства необходимо нажать клавиши + ;
написать функцию Find(x),гдеx –искомое неизвестное;
нажать клавишу .(знак равенства).

Технология решения уравнения 3 Х — 1,6е Х +4 приведена на рис. 4.3.

X:=2.5 Given 3 Х – 1.6exp(x)+4,x=0 Find(x)=2.541

X:=4.5 Given 3 Х – 1.6exp(x)+4,x=0 Find(x)=4.472

Рис. 4.3. Решение уравнения 3 Х – 1,6e X +4

Определение корней многочлена с помощью функции polyroots

Корни многочлена обычно определяются с помощью функции polyroots, которая имеет вид:

где V – вектор коэффициентов многочлена, начиная с младшей степени.

Функция находит все вещественные и комплексные корни.

Технология решения задачи состоит в следующем:

ввести символ присвоения имени вектора-столбца, например V:=;
нажать комбинацию клавиш Ctrl+M. На экране появляется окно InsertMatrix.В полях Rows и Columns устанавливается число строк и число столбцов матрицы. Для случая определения корней полинома число столбцов равно 1, а число строк – (n+1), где n степень многочлена. После щелчка по кнопке ОК в окне, на экране появляется пустой шаблон вектора- столбца размером (n+1) ×1;
заполнить маркеры ввода вектора коэффициентами заданного полинома, в первой строке пишется коэффициент свободного члена (коэффициент при нулевой степени полинома);
написать polyroots (V);
нажать клавишу = (равно) на клавиатуре. На экране появится ответ в виде вектора корней.

Пример 4.2.Решить уравнениеx 4 +3x 3 -7x+3.5=0

Технология выполнения задания приведена на рис. 4.4.

Рис. 4.4. Решение уравненияx 4 +3x 3 -7x+3.5=0.

Возьмите из Задания 4.1 и Задания 4.2 свой вариант уравнения и найдите его корни используя функцию root и функцию polyroots. Убедитесь, что найденные значения действительно являются корнями Вашего уравнения.

Задание 4.1. Найти все корни заданного уравнения, используя функцию root

№п.п.	Уравнение f(x)	№ п.п.	Уравнение f(x)
4sin x + x 2 — 2=0	(x — 1) 2 — 0.5exp( — x) – 2=0
3 X -4.5x-5.6=0	2/x+x 2 + e x – 8=0
3 sinÖx +0.35x-8x=0	tgx + x + 2=0
0.25x 2 +x-1.25002=0	ctgx – 2x + 2=0
0.1x 2 -xlnx=0	-x 2 + cos (x+1) + 3=0
3x — 4lnx-5=0	2ln(2–x)–x + e x – 10=0
e x — e –x -2=0	1/x + ln(2x + 4) – 3=0
e x + lnx – 10x=0	x× cos x + 1.5=0
sin x 2 +cos x 2 -10x=0	2x 5 – lnx – 7x 2 =0
x 2 -ln(1+x)-3=0	x×sinx x + 1.5=0
2xsin x – cosx=0	x2 x – 4x 2 + 1.5=0
lnx – x + 1.8=0	2.5 x – 8.6x – 3.5=0
0.6 ×3 x – 2.3x – 3=0	ln(x + 2) + 2x 2 — 9x + 2=0
2 x – 4x=0	xln(2.5x) – 1.5x + 1.5=0
3x – e x + 4=0	xtgx – 1/3=0