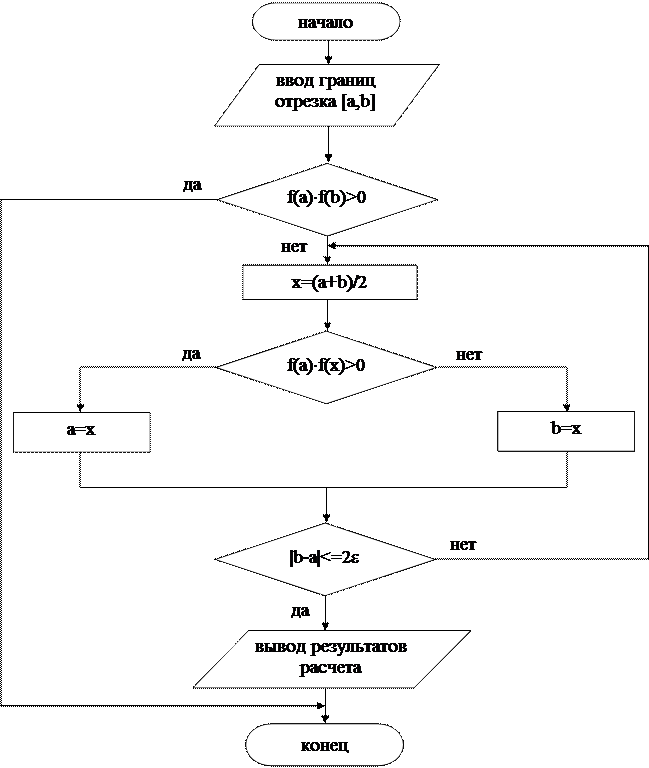
Постановка задачи. Пусть дана некоторая функция f(x). Необходимо найти с точностью до e такое x* , что f(x*)=0 . В том случае, когда решение не может быть найдено в явном виде, применяются численные методы. Наиболее распространенными из них являются метод деления отрезка пополам, метод простых итераций, метод касательных (Ньютона), метод секущих и метод хорд.
Рассмотрим метод деления отрезка пополам более подробно.
В соответствии с этим методом вначале необходимо приблизительно определить отрезок, на котором функция f(x) меняет знак. Для этого можно использовать графический способ, заключающийся в построении графика функции на экране компьютера и приблизительного визуального определения точек пересечения графика с осью абсцисс.
 | · Простота; · Быстрое достижение результата. |
 | · Необходимо заранее знать отрезок, на котором функция меняет знак, что не совсем удобно. · Линейная сходимость. |
Блок-схема
алгоритма поиска корня уравнения f(x)=0
Методом деления отрезка пополам
Метод хорд.
Является более быстрым способом нахождения корня уравнения f(x)=0 лежащего на отрезке [a;b], таком, что f(a)*f(b) 0. Разделим отрезок в отношении
Это даёт приближённое значение корня x1=a+h1 ,
Применяя этот приём, к тому из отрезков [a;x1] или [x1;b] на концах которого функция имеет противоположные знаки. Получим второе приближение корня x2.
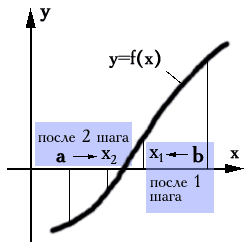
Геометрически, метод хорд эквивалентен замене кривой y=f(x) хордой проходящей через т. а и т. B.
Полагая, что х=х1 и у=0, получим х1=а — f(a)*(b-a)/(f(b)-f(a)), x1 – первое приближение.
Для сходимости процессов корень должен быть отделён вторая производная должна сохранять знак на отрезке [a;b].
Процесс вычисления заканчивается когда разность между 2-мя значениями корня
│f(x)│ 0 , то разделим первое уравнение на а11 и умножим
на а21 . Вычтем из второго уравнения преобразованное первое. Получим :
Сейчас легко находим v:
Аналогично для матриц большего порядка.
Метод итерации.
При большом числе неизвестных используют приближённо-численные методы.
|a11 a12 … a1n| |B1| |x1|
A=| a21 a22 … a2n| B= |B2 x=|x2|
|an1 an2 … ann| |Bn| |xn|
Предположим, что аii0. Разрешим первое уравнение относительно х1, второе относительно х2 и т.д.
Далее решаем методом последовательных приближений. За начальное приближение выбираем столбец свободных членов:
Алгоритм нахождения корней:
Вычисление заканчивается тогда, когда разность между 2-мя ближними итерациями значений корня будет 2 + a3t 3 + a4t 4 + … + ant n
по схеме Горнера представляется в виде
Данное разложение полинома удобно тем, что в нём отсутствует возведение в степень, что значительно ускоряет вычисление полинома.
Что вызывает тренды на фондовых и товарных рынках Объяснение теории грузового поезда Первые 17 лет моих рыночных исследований сводились к попыткам вычислить, когда этот.
Что делает отдел по эксплуатации и сопровождению ИС? Отвечает за сохранность данных (расписания копирования, копирование и пр.).
ЧТО И КАК ПИСАЛИ О МОДЕ В ЖУРНАЛАХ НАЧАЛА XX ВЕКА Первый номер журнала «Аполлон» за 1909 г. начинался, по сути, с программного заявления редакции журнала.
ЧТО ПРОИСХОДИТ ВО ВЗРОСЛОЙ ЖИЗНИ? Если вы все еще «неправильно» связаны с матерью, вы избегаете отделения и независимого взрослого существования.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
Видео:Численное решение уравнений, урок 2/5. Метод деления отрезка пополамСкачать

Метод бисекции
Метод бисекции или метод деления отрезка пополам — простейший численный метод приближённого нахождения корня уравнения.
Калькулятор, который находит приближенное решение уравнения методом бисекции или методом деления отрезка пополам. Небольшая теория под калькулятором.
Метод бисекции
Метод бисекции
Существует довольно очевидная теорема: «Если непрерывная функция на концах некоторого интервала имеет значения разных знаков, то внутри этого интервала у нее есть корень (как минимум, один, но может быть и несколько)». На базе этой теоремы построено несколько методов численного нахождения приближенного значения корня функции. Обобщенно все эти методы называются методами дихотомии, т. е. методами деления отрезка на две части (необязательно равные).
Здесь уже были рассмотрены Метод хорд и Метод секущих, теперь дошла очередь и до самого простого метода дихотомии, называемого методом бисекции, или методом деления отрезка пополам. Как следует из названия, именно в этом методе отрезок делится каждый раз на две равные части. Середина отрезка считается следующим приближением значения корня. Вычисляется значение функции в этой точке, и, если критерий останова не достигнут, выбирается новый интервал. Интервал выбирается таким образом, чтобы на его концах значения функции по прежнему имели разный знак, то есть чтобы он по прежнему содержал корень. Такой подход обеспечивает гарантированную сходимость метода независимо от сложности функции — и это весьма важное свойство. Недостатком метода является то же самое — метод никогда не сойдется быстрее, т. е. сходимость метода всегда равна сходимости в наихудшем случае.
Итерационная формула проста:
Метод бисекции является двухшаговым, то есть новое приближение определяется двумя предыдущими итерациями. Поэтому необходимо задавать два начальных приближения корня.
Метод требует, чтобы начальные точки были выбраны по разные стороны от корня (то есть корень содержался в выбранном интервале).
В качестве критерия останова берут один из следующих:
— значение функции на данной итерации стало меньше заданого ε.
— изменение хk в результате итерации стало меньше заданого ε. Поскольку интервал на каждом шаге уменьшается в два раза, вместо проверки x можно рассчитать количество требуемых итераций.
Видео:Алгоритмы. Нахождение корней уравнений методом деления отрезка пополам.Скачать

Метод решения уравнений f x 0 методом деления отрезка пополам
Pers.narod.ru. Обучение. Лекции по численным методам. Приближённое решение нелинейных алгебраических уравнений
1. Приближенное решение нелинейных алгебраических уравнений
Дано нелинейное алгебраическое уравнение
Нелинейность уравнения означает, что график функции не есть прямая линия, т.е. в f(x) входит x в некоторой степени или под знаком функции.
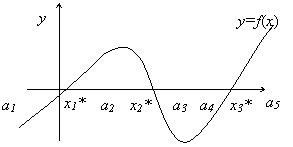
Решить уравнение – это найти такое x* ∈ R: f(x*)=0. Значение x* называют корнем уравнения. Нелинейное уравнение может иметь несколько корней. Геометрическая интерпретация корней уравнения представлена на рис. 1. Корнями уравнения (1) являются точки x1*, x2*, x3*, в которых функция f(x) пересекает ось x.
В приближенных методах процесс нахождения решения, вообще говоря, бесконечен. Решение получается в виде бесконечной последовательности <xn>, такой, что 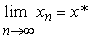
Если корней несколько, то для каждого нужно найти интервал изоляции.
Существуют различные способы исследования функции: аналитический, табличный, графический.
Аналитический способ состоит в нахождении экстремумов функции f(x), исследование ее поведения при 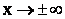
Графический способ – это построение графика функции f(x) и определение числа корней по количеству пересечений графика с осью x.
Табличный способ – это построение таблицы, состоящей из столбца аргумента x и столбца значений функции f(x). О наличии корней свидетельствуют перемены знака функции. Чтобы не произошла потеря корней, шаг изменения аргумента должен быть достаточно мелким, а интервал изменения достаточно широким.
Решить уравнение x 3 ‑ 6x 2 +3x+11=0, т.е. f(x)= x 3 ‑ 6x 2 +3x+11.
Найдем производную f / (x)=3x 2 -12x+3.
Найдем нули производной f / (x)=3x 2 -12x+3=0; D=144-4*3*3=108;
X1=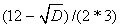
X2=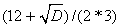
Так как f / (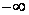
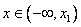
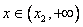
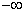
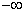
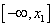
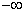
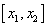
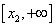
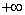
Найдем интервалы изоляции для каждого из корней.
Рассмотрим для первого корня отрезок [-2, -1]:
f(-2)= -27 0, f / (x)>0 при 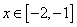
Рассмотрим для второго корня отрезок [1, 3]:
f(1)= 9>0, f(3)= -7 / (x) 0, f / (x)>0 при 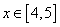
Видео:Метод половинного деления решение нелинейного уравненияСкачать

Метод деления отрезка пополам (метод бисекции)
Один из простейших методов нахождения корней нелинейных уравнений состоит в следующем. Допустим, что нам удалось найти отрезок [а, b], на котором расположено искомое значение корня (далее мы предполагаем, что х = с – единственный корень на отрезке [а, b], а если корней на [а, b] несколько, то в результате применения метода деления отрезка пополам и метода хорд (см. разд. 1.1.3) будет найдено приближенное значение одного из корней) х = с, т.е. 
В качестве начального приближения корня с0 принимаем середину этого отрезка: с0=(а+b)/2. Далее исследуем значения функции F(x) на концах отрезков [а, с0] и [с0, b], т.е. в точках а, с0, b. Тот из отрезков, на концах которого F(x) принимает значения разных знаков, содержит искомый корень; поэтому его принимаем в качестве нового отрезка [a1,b1]. Вторую половину отрезка [а, b], на которой знак F(x) не меняется, отбрасываем. В качестве первого приближения корня принимаем середину нового отрезка c1 = (a1+b1)/2 и т.д. Таким образом, k-е приближение вычисляем как

После каждой итерации отрезок, на котором расположен корень, уменьшается вдвое, а после kитераций он сокращается в 2kраз:

Пусть приближенное решение 

Взяв в качестве приближенного решения k-еприближение корня: 


Из (1.2) следует, что (1.5) выполнено, если

Таким образом, итерационный процесс нужно продолжать до тех пор, пока не будет выполнено условие (1.6).
Метод деления отрезка пополам проиллюстрирован на рис. 1.1. Пусть для определенности F(a) 0. В качестве начального приближения корня примем с0 = (а + b)/2. Поскольку в рассматриваемом случае F(c0) 0 и F(b) > 0. Таким образом, с
Рис. 1.1. Метод деления отрезка пополам
В отличие от большинства других итерационных методов метод деления отрезка пополам всегда сходится, причем можно гарантировать, что полученное решение будет иметь любую наперед заданную точность (разумеется, в рамках разрядности компьютера). При применении этого метода нет необходимости приближенно определять момент достижения требуемой точности, пользуясь, например, условиями близости двух последовательных приближений (2.22) или (2.23) (записанными для скалярного случая). Вместо них применяется соотношение (1.6), гарантирующее выполнение (1.4).
Однако метод деления отрезка пополам довольно медленный. Вычислим число итераций N, требуемое для достижения точности ε. Для этого выясним, пользуясь (1.3), для каких kвыполнено условие (1.6), и возьмем в качестве N наименьшее из таких k. Окончательно получим

где Е(х) – целая часть числа х. Обычно для метода деления отрезка пополам N больше, чем для некоторых других методов, что не является препятствием к применению этого метода, если каждое вычисление значения функции F(x) несложно.
Итерационный процесс можно завершать и тогда, когда значение функции F(x) после k-й итерации станет меньшим по модулю ε, т.е.

Такое условие окончания итераций аналогично условию (2.24). Действительно, для уравнения (1.1) величина F(ck)есть невязка(см. разд. 2.2.2),полученная на k—йитерации.
На рис. 1.2 представлен алгоритм итерационного процесса нахождения корня уравнения (1.1) методом деления отрезка пополам. Здесь сужение отрезка осуществляется заменой границ а или bна текущее значение корня с. При этом значение F(a) вычисляют лишь один раз, поскольку нам нужен только знак функции F(x) на левой границе, а он в процессе итераций не меняется.
Рис. 1.2. Алгоритм метода деления отрезка пополам
💡 Видео
1.1 Решение нелинейных уравнений метод деления отрезка пополам (бисекций) Мathcad15Скачать

Метод Ньютона (метод касательных) Пример РешенияСкачать

Решение нелинейного уравнения методом деления отрезка пополамСкачать

Решение уравнений методом деления отрезка пополам в табличных процессорахСкачать

Метод простых итераций пример решения нелинейных уравненийСкачать

Урок 10. C++ Метод половинного деленияСкачать

5.1 Численные методы решения уравнений F(x)=0Скачать

Деление отрезка пополамСкачать

14 Метод половинного деления Ручной счет Численные методы решения нелинейного уравненияСкачать

Метод половинного деления. ДихотомияСкачать

Численное решение уравнений, урок 1/5. Локализация корняСкачать
Методы деления отрезка пополам и золотого сеченияСкачать

Метод половинного деления - ВизуализацияСкачать

Метод деления отрезка пополам и градиентного спускаСкачать

6 Метод половинного деления C++ Численные методы решения нелинейного уравненияСкачать

Метод дихотомииСкачать

Решение уравнений (метод дихотомии) на C#Скачать