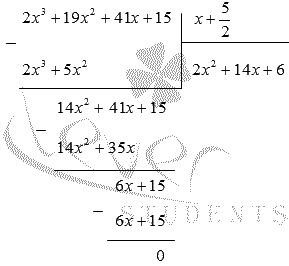- Главная
- Список секций
- Математика
- Методы решения алгебраических уравнений высших степеней
- Методы решения алгебраических уравнений высших степеней
- Лекция по теме «Уравнения высших степеней. Методы их решения». 9-й класс
- Разложение многочлена на множители
- Теория
- Основная теорема алгебры
- Теорема Безу
- Следствие из теоремы Безу
- Разложение на множители квадратного трехчлена
- Способы разложения на множители многочлена степени выше второй
- Вынесение общего множителя за скобки
- Разложение на множители многочлена с рациональными корнями
- Искусственные приемы при разложении многочлена на множители
- Способ группировки
- Использование формул сокращенного умножения и бинома Ньютона для разложения многочлена на множители
- Способ замены переменной при разложении многочлена на множители
- 📽️ Видео
Видео:Как решать уравнения высших степеней, очень лёгкий способ!!!Скачать

Методы решения алгебраических уравнений высших степеней
Автор работы награжден дипломом победителя II степени
Математическое образование, получаемое в общеобразовательной школе, является важнейшим компонентом общего образования и общей культуры современного человека. Практически все, что окружает современного человека – это все так или иначе связано с математикой. А последние достижения в физике, технике и информационных технологиях не оставляют никакого сомнения, что и в будущем положение вещей останется прежним. Поэтому решение многих практических задач сводится к решению различных видов уравнений, которые необходимо научиться решать.
Актуальность проблемы : отсутствие навыков решения уравнений высших степеней различными способами у учащихся мешает им успешно подготовиться к итоговой аттестации по математике и математическим олимпиадам, обучению в профильном математическом классе. При подготовке к экзамену в 9 классе я встретилась с уравнениями степени выше второй. Было понятно, что решать уравнения необходимо разложением на множители, но не все уравнения удавалось решить. Поэтому, обучаясь уже в 10 классе, я решила исследовать какие еще существуют методы решения уравнения.
Гипотеза: Знание методов решения различных уравнений значительно упростит нахождение корней, а также сэкономить время при решении уравнений.
Объект исследования: уравнения высших степеней
Предмет исследования – способы решения уравнений высших степеней.
Методы исследования: теоретические: изучение литературы по теме исследования, изучение тематических Интернет-ресурсов; анализ полученной информации; сравнение способов решения уравнений на удобство и рациональность.
Цель: Узнать какие методы решения высших степеней существуют; Научиться решать уравнения высших степеней различными способами.
Исследовать историю возникновения методов решений.
Найти различные методы и приёмы решения уравнений высших степеней
Практически выяснить, какой из способов более понятен для 9-ых классов.
Решение уравнений высших степеней – история полная драматизма, разочарования и радости открытия. В течение почти 700 лет математики разных стран пытались найти приёмы решения уравнений третьей, четвёртой и более высоких степеней.
Только в 11 веке таджикский поэт и ученый Омар Хаям впервые решил уравнение III степени. Установить, существует ли формула для нахождения корней любого уравнения, пытались многие. В конце 18 века французский ученый Луи Лагранж пытался доказать невозможность алгоритма общих уравнений, а вначале 19 века француз Галуа развил идею Лагранжа.
С тех пор математика пошла другим путем. Ученые стали искать другие методы решения уравнений высших степеней.
Из общих методов решения уравнений высших степеней, которые встречаются чаще всего, используют: метод разложения левой части уравнения на множители; метод замены переменной (метод введения новой переменной); графический способ. С этими методами мы знакомимся в 9 классе при изучении темы: «Целое уравнение и его корни». В учебнике Алгебра 9 (авторы Макарычев Ю.Н., Миндюк Н.Г и др) последних годов издания достаточно подробно рассматриваются основные методы решения уравнений высших степеней.
Рассмотрим некоторые из них.
Разложение многочлена на множители.
При разложении на множители многочлена степени выше второй не существует универсального метода решения.
Так одним из способов является способ группировки.
Данный способ применяют к многочленам, которые не имеют общего множителя для всех членов многочлена. Чтобы разложить многочлен на множители способом группировки, нужно: Объединить члены многочлена в такие группы, которые имеют общий множитель в виде многочлена. Вынести этот общий множитель за скобки.
Примеры решения уравнений способом группировки:
x⁴-5x³-20x²+4x²+100х-80=0 («искусственно» -16х 2 =-20x²+4x²)
x²(x²-20)-5x(x²-20)+4(x²-20)=0 (нужно догадаться как сгруппировать)
Еще один способ: по формулам сокращенного умножения
1. Квадрат суммы: (a + b) 2 = a 2 + 2ab + b 2
2. Квадрат разности: (a — b) 2 = a 2 — 2ab + b 2
3. Разность квадратов: а 2 — b 2 = (a — b) (a + b)
4. Кубсуммы : (a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3
5. Кубразности : (a — b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3
6. Суммакубов : a 3 + b 3 = (a + b) (a 2 — ab + b 2 )
7. Разностькубов : a 3 — b 3 = (a — b) (a 2 + ab + b 2 )
Ответ: корней нет.
Метод введения новой переменной:
К квадратным уравнениям сводятся уравнения четвертой степени: ax 4 + bx 2 + c = 0, называемые биквадратными, причем, а ≠ 0. Достаточно положить в этом уравнении х 2 = y, следовательно, ay² + by + c = 0. Найдём корни полученного квадратного уравнения y1,2 =
заменим y на x и получим
Примеры решения уравнения методом введения новой переменной:
(x 2 +4x)(x 2 +4x-17)=-60
— 17t = -60
t 2 — 17t + 60 = 0
Но не всегда удается решить уравнения степени выше второй указанными методами.
Попробуем решить уравнение используя выше изложенные приёмы. НЕ УДАЕТСЯ.
В учебнике Ю.М. Колягин, М.В. Ткачева «Алгебра и начала анализа» для 10 класса сказано, что вычислять значения многочленов в математике приходится довольно часто и важно делать это как можно проще.
Если это уравнение имеет целый корень, то он является делителем свободного члена (-1), т.е. равняется одному из чисел: . Проверка показывает, что корнем уравнения является число -1. Значит, многочлен можно представить в виде произведения , т.е. многочлен можно без остатка разделить на двучлен . Выполним такое деление “уголком”:
Таким образом, мы фактически разложили левую часть уравнения на множители:
Произведение множителей равно нулю, если один из множителей равен нулю. Получаем два уравнения:
Итак, данное уравнение имеет три корня:
Наиболее известный способ вычисления многочленов называется схемой Горнера в честь английского математика Уильяма Горнера (1786-1837).
Горнер Уильям Джордж (1786 — 1837) — английский математик. Родился в городе Бристоль в Англии.
Основные труды относятся к решению алгебраических уравнений. В 1819 году опубликовал способ приближённого вычисления действительных корней многочлена, который называется теперь способом Руффини-Горнера (этот способ был известен китайцам еще в XIII веке). Работа была напечатана в философских работах Королевского научного сообщества.
Схема Горнера – способ деления многочлена
на бином x−a . Работать придётся с таблицей, первая строка которой содержит коэффициенты заданного многочлена. Первым элементом второй строки будет число a , взятое из бинома x−a :
Первую строку заполнили. Вторая заполняется по следующему правилу:
Видео:Вспоминаем схему Горнера и уравнения высших степенейСкачать

Лекция по теме «Уравнения высших степеней. Методы их решения». 9-й класс
Разделы: Математика
Класс: 9
- Закрепить понятие целого рационального уравнения -й степени.
- Сформулировать основные методы решения уравнений высших степеней (n > 3).
- Обучить основным методам решения уравнений высших степеней.
- Научить по виду уравнения определять наиболее эффективный способ его решения.
Формы, методы и педагогические приемы, которые используются учителем на уроке:
- Лекционно-семинарская система обучения (лекции – объяснение нового материала, семинары – решение задач).
- Информационно-коммуникационные технологии (фронтальный опрос, устная работа с классом).
- Дифференцированное обучение, групповые и индивидуальные формы.
- Использование исследовательского метода в обучении, направленного на развитие математического аппарата и мыслительных способностей каждого конкретного ученика.
- Печатный материал – индивидуальный краткий конспект урока (основные понятия, формулы, утверждения, материал лекций сжато в виде схем или таблиц).
- Организационный момент.
Цель этапа: включить учащихся в учебную деятельность, определить содержательные рамки урока. - Актуализация знаний учащихся.
Цель этапа: актуализировать знания учащихся по изученным ранее смежным темам - Изучение новой темы (лекция). Цель этапа: сформулировать основные методы решения уравнений высших степеней (n > 3)
- Подведение итогов.
Цель этапа: еще раз выделить ключевые моменты в материале, изученном на уроке. - Домашнее задание.
Цель этапа: сформулировать домашнее задание для учащихся.
1. Организационный момент.
Формулировка темы урока: “Уравнения высших степеней. Методы их решения”.
2. Актуализация знаний учащихся.
Теоретический опрос – беседа. Повторение некоторых ранее изученных сведений из теории. Учащиеся формулируют основные определения и дают формулировки необходимых теорем. Приводят примеры, демонстрируя уровень полученных ранее знаний.
- Понятие уравнения с одной переменной.
- Понятие корня уравнения, решения уравнения.
- Понятие линейного уравнения с одной переменной, понятие квадратного уравнения с одной переменной.
- Понятие равносильности уравнений, уравнения-следствия (понятие посторонних корней), переход не по следствию (случай потери корней).
- Понятие целого рационального выражения с одной переменной.
- Понятие целого рационального уравнения n-й степени. Стандартный вид целого рационального уравнения. Приведенное целое рациональное уравнение.
- Переход к совокупности уравнений более низких степеней путем разложения исходного уравнения на множители.
- Понятие многочлена n-й степени от x. Теорема Безу. Следствия из теоремы Безу. Теоремы о корнях (Z-корни и Q-корни) целого рационального уравнения с целыми коэффициентами (соответственно приведенного и неприведенного).
- Схема Горнера.
3. Изучение новой темы.
Будем рассматривать целое рациональное уравнение n-й степени стандартного вида с одной неизвестной переменной x : Pn(x) = 0 , где Pn(x) = anx n + an-1x n-1 + a1x + a0 – многочлен n-й степени от x, an ≠ 0 . Если an = 1 то такое уравнение называют приведенным целым рациональным уравнением n-й степени. Рассмотрим такие уравнения при различных значениях n и перечислим основные методы их решения.
n = 1 – линейное уравнение.
n = 2 – квадратное уравнение. Формула дискриминанта. Формула для вычисления корней. Теорема Виета. Выделение полного квадрата.
n = 3 – кубическое уравнение.
Пример: x 3 – 4x 2 – x + 4 = 0 

Возвратное кубическое уравнение вида ax 3 + bx 2 + bx + a = 0. Решаем, объединяя члены с одинаковыми коэффициентами.
Пример: x 3 – 5x 2 – 5x + 1 = 0 



Уравнение с целыми коэффициентами. Подбор Z-корней на основании теоремы. Схема Горнера. При применении этого метода необходимо сделать акцент на том, что перебор в данном случае конечный, и корни мы подбираем по определенному алгоритму в соответствии с теоремой о Z-корнях приведенного целого рационального уравнения с целыми коэффициентами.
Пример: x 3 – 9x 2 + 23x – 15 = 0. Уравнение приведенное. Выпишем делители свободного члена <+1; +3; +5; +15>. Применим схему Горнера:
| x 3 | x 2 | x 1 | x 0 | вывод | |
| 1 | -9 | 23 | -15 | ||
| 1 | 1 | 1 х 1 – 9 = -8 | 1 х (-8) + 23 = 15 | 1 х 15 – 15 = 0 | 1 – корень |
| x 2 | x 1 | x 0 |
Получаем 

Уравнение с целыми коэффициентами. Подбор Q-корней на основании теоремы. Схема Горнера. При применении этого метода необходимо сделать акцент на том, что перебор в данном случае конечный и корни мы подбираем по определенному алгоритму в соответствии с теоремой о Q-корнях неприведенного целого рационального уравнения с целыми коэффициентами.
Пример: 9x 3 + 27x 2 – x – 3 = 0. Уравнение неприведенное. Выпишем делители свободного члена <+1; +3>. Выпишем делители коэффициента при старшей степени неизвестного. <+1; +3; +9> Следовательно, корни будем искать среди значений <+1; +

| x 3 | x 2 | x 1 | x 0 | вывод | |
| 9 | 27 | -1 | -3 | ||
| 1 | 9 | 1 x 9 + 27 = 36 | 1 x 36 – 1 = 35 | 1 x 35 – 3 = 32 ≠ 0 | 1 – не корень |
| -1 | 9 | -1 x 9 + 27 = 18 | -1 x 18 – 1 = -19 | -1 x (-19) – 3 = 16 ≠ 0 | -1 – не корень |
 | 9 |  x 9 + 27 = 30 x 9 + 27 = 30 |  x 30 – 1 = 9 x 30 – 1 = 9 |  x 9 – 3 = 0 x 9 – 3 = 0 | корень |
| x 2 | x 1 | x 0 |
Получаем 




Для удобства подсчета при подборе Q-корней бывает удобно сделать замену переменной, перейти к приведенному уравнению и подбирать Z-корни.
- Если можно воспользоваться заменой вида y = kx.
Формула Кардано. Существует универсальный метод решения кубических уравнений – это формула Кардано. Эту формулу связывают с именами итальянских математиков Джероламо Кардано (1501–1576), Николо Тарталья (1500–1557), Сципиона дель Ферро (1465–1526). Эта формула лежит за рамками нашего курса.
n = 4 – уравнение четвертой степени.
Пример: x 4 + 2x 3 + 5x 2 + 4x – 12 = 0 



Метод замены переменной.
- Возвратное уравнение четвертой степени вида ax 4 + bx 3 + cx 2 + bx + a = 0.
Решаем, объединяя члены с одинаковыми коэффициентами, путем замены вида
- Обобщенное возвратное уравнение четвертой степени вида ax 4 + bx 3 + cx 2 – bx + a = 0.
- Обобщенное возвратное уравнение четвертой степени вида ax 4 + bx 3 + cx 2 + kbx + k 2 a = 0.
- Замена общего вида. Некоторые стандартные замены.
Пример 3. Замена общего вида (вытекает из вида конкретного уравнения).
Уравнение с целыми коэффициентами. Подбор Z-корней на основании теоремы. Схема Горнера. Алгоритм аналогичен рассмотренному выше для n = 3.
Уравнение с целыми коэффициентами. Подбор Q-корней на основании теоремы. Схема Горнера. Алгоритм аналогичен рассмотренному выше для n = 3.
Формула общего вида. Существует универсальный метод решения уравнений четвертой степени. Эту формулу связывают с именем Людовико Феррари (1522–1565). Эта формула лежит за рамками нашего курса.
n > 5 – уравнения пятой и более высоких степеней.
Уравнение с целыми коэффициентами. Подбор Z-корней на основании теоремы. Схема Горнера. Алгоритм аналогичен рассмотренному выше для n = 3.
Уравнение с целыми коэффициентами. Подбор Q-корней на основании теоремы. Схема Горнера. Алгоритм аналогичен рассмотренному выше для n = 3.
Симметрические уравнения. Любое возвратное уравнение нечетной степени имеет корень x = -1 и после разложения его на множители получаем, что один сомножитель имеет вид (x + 1), а второй сомножитель – возвратное уравнение четной степени (его степень на единицу меньше, чем степень исходного уравнения). Любое возвратное уравнение четной степени вместе с корнем вида x = φ содержит и корень вида 
Метод замены переменной. Использование однородности.
Не существует формулы общего вида для решения целых уравнений пятой степени (это показали итальянский математик Паоло Руффини (1765–1822) и норвежский математик Нильс Хенрик Абель (1802–1829)) и более высоких степеней (это показал французский математик Эварист Галуа (1811–1832)).
- Напомним еще раз, что на практике возможно использование комбинации перечисленных выше методов. Удобно переходить к совокупности уравнений более низких степеней путем разложения исходного уравнения на множители.
- За рамками нашего сегодняшнего обсуждения остались широко используемые на практике графические методы решения уравнений и методы приближенного решения уравнений высших степеней.
- Бывают ситуации, когда у уравнения нет R-корней. Тогда решение сводится к тому, чтобы показать, что уравнение корней не имеет. Для доказательства анализируем поведение рассматриваемых функций на промежутках монотонности. Пример: уравнение x 8 – x 3 + 1 = 0 не имеет корней.
- Использование свойства монотонности функций. Бывают ситуации, когда использование различных свойств функций позволяет упростить поставленную задачу.
Пример 1: уравнение x 5 + 3x – 4 = 0 имеет один корень x = 1. По свойству монотонности анализируемых функций других корней нет.
Пример 2: уравнение x 4 + (x – 1) 4 = 97 имеет корни x1 = -2 и x2 = 3. Проанализировав поведение соответствующих функций на промежутках монотонности, заключаем, что других корней нет.
4. Подведение итогов.
Резюме: Теперь мы овладели основными методами решения различных уравнений высших степеней (для n > 3). Наша задача научиться эффективно использовать перечисленные выше алгоритмы. В зависимости от вида уравнения мы должны будем научиться определять, какой способ решения в данном случае является наиболее эффективным, а также правильно применять выбранный метод.
5. Домашнее задание.
[1]: п.7, стр. 164–174, №№ 33–36, 39–44, 46,47.
[4]: №№ 9.1–9.4, 9.6–9.8, 9.12, 9.14–9.16, 9.24–9.27.
Возможные темы докладов или рефератов по данной тематике:
- Формула Кардано
- Графический метод решения уравнений. Примеры решения.
- Методы приближенного решения уравнений.
Анализ усвоения материала и интереса учащихся к теме:
Опыт показывает, что интерес учащихся в первую очередь вызывает возможность подбора Z-корней и Q-корней уравнений при помощи достаточно простого алгоритма с использованием схемы Горнера. Также учащиеся интересуются различными стандартными типами замены переменных, которые позволяют существенно упрощать вид задачи. Особый интерес обычно вызывают графические методы решения. В этом случае дополнительно можно разобрать задачи на графический метод решения уравнений; обсудить общий вид графика для многочлена 3, 4, 5 степени; проанализировать, как связано число корней уравнений 3, 4, 5 степени с видом соответствующего графика. Ниже приведен список книг, в которых можно найти дополнительную информацию по данной тематике.
- Виленкин Н.Я. и др. “Алгебра. Учебник для учащихся 9 классов с углубленным изучением математики” – М., Просвещение, 2007 – 367 с.
- Виленкин Н.Я., Шибасов Л.П., Шибасова З.Ф. “За страницами учебника математики. Арифметика. Алгебра. 10-11 класс” – М., Просвещение, 2008 – 192 с.
- Выгодский М.Я. “Справочник по математике” – М., АСТ, 2010 – 1055 с.
- Галицкий М.Л. “Сборник задач по алгебре. Учебное пособие для 8-9 классов с углубленным изучением математики” – М., Просвещение, 2008 – 301 с.
- Звавич Л.И. и др. “Алгебра и начала анализа. 8–11 кл. Пособие для школ и классов с углубленным изучением математики” – М., Дрофа, 1999 – 352 с.
- Звавич Л.И., Аверьянов Д.И., Пигарев Б.П., Трушанина Т.Н. “Задания по математике для подготовки к письменному экзамену в 9 классе” – М., Просвещение, 2007 – 112 с.
- Иванов А.А., Иванов А.П. “Тематические тесты для систематизации знаний по математике” ч.1 – М., Физматкнига, 2006 – 176 с.
- Иванов А.А., Иванов А.П. “Тематические тесты для систематизации знаний по математике” ч.2 – М., Физматкнига, 2006 – 176 с.
- Иванов А.П. “Тесты и контрольные работы по математике. Учебное пособие”. – М., Физматкнига, 2008 – 304 с.
- Лейбсон К.Л. “Сборник практических заданий по математике. Часть 2–9 класс” – М., МЦНМО, 2009 – 184 с.
- Макарычев Ю.Н., Миндюк Н.Г. “Алгебра. Дополнительные главы к школьному учебнику 9 класса. Учебное пособие для учащихся школ и классов с углубленным изучением математики.” – М., Просвещение, 2006 – 224 с.
- Мордкович А.Г. “Алгебра. Углубленное изучение. 8 класс. Учебник” – М., Мнемозина, 2006 – 296 с.
- Савин А.П. “Энциклопедический словарь юного математика” – М., Педагогика, 1985 – 352 с.
- Сурвилло Г.С., Симонов А.С. “Дидактические материалы по алгебре для 9 класса с углубленным изучением математики” – М., Просвещение, 2006 – 95 с.
- Чулков П.В. “Уравнения и неравенства в школьном курсе математик. Лекции 1–4” – М., Первое сентября, 2006 – 88 с.
- Чулков П.В. “Уравнения и неравенства в школьном курсе математик. Лекции 5–8” – М., Первое сентября, 2009 – 84 с.
Видео:11 класс, 3 урок, Уравнения высших степенейСкачать

Разложение многочлена на множители
Для того, чтобы разложить на множители, необходимо упрощать выражения. Это необходимо для того, чтобы можно было в дальнейшем сократить. Разложение многочлена имеет смысл тогда, когда его степень не ниже второй. Многочлен с первой степенью называют линейным.
Статья раскроет все понятия разложения, теоретические основы и способы разложений многочлена на множители.
Видео:Уравнение четвертой степениСкачать

Теория
Когда любой многочлен со степенью n , имеющие вид P n x = a n x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 , представляют в виде произведения с постоянным множителем со старшей степенью a n и n линейных множителей ( x — x i ) , i = 1 , 2 , … , n , тогда P n ( x ) = a n ( x — x n ) ( x — x n — 1 ) · . . . · ( x — x 1 ) , где x i , i = 1 , 2 , … , n – это и есть корни многочлена.
Теорема предназначена для корней комплексного типа x i , i = 1 , 2 , … , n и для комплексных коэффициентов a k , k = 0 , 1 , 2 , … , n . Это и есть основа любого разложения.
Когда коэффициенты вида a k , k = 0 , 1 , 2 , … , n являются действительными числами, тогда комплексные корни, которые будут встречаться сопряженными парами. Например, корни x 1 и x 2 , относящиеся к многочлену вида P n x = a n x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 считаются комплексно сопряженным, тогда другие корни являются действительными, отсюда получаем, что многочлен примет вид P n ( x ) = a n ( x — x n ) ( x — x n — 1 ) · . . . · ( x — x 3 ) x 2 + p x + q , где x 2 + p x + q = ( x — x 1 ) ( x — x 2 ) .
Замечание
Корни многочлена могут повторяться. Рассмотрим доказательство теоремы алгебры, следствия из теоремы Безу.
Видео:Схема Горнера. 10 класс.Скачать

Основная теорема алгебры
Любой многочлен со степенью n имеет как минимум один корень.
Видео:Теорема Виета для многочлена 3 порядка. 10 класс.Скачать

Теорема Безу
После того, как произвели деление многочлена вида P n x = a n x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 на ( x — s ) , тогда получаем остаток, который равен многочлену в точке s , тогда получим
P n x = a n x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 = ( x — s ) · Q n — 1 ( x ) + P n ( s ) , где Q n — 1 ( x ) является многочленом со степенью n — 1 .
Следствие из теоремы Безу
Когда корень многочлена P n ( x ) считается s , тогда P n x = a n x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 = ( x — s ) · Q n — 1 ( x ) . Данное следствие является достаточным при употреблении для описания решения.
Видео:Теорема БезуСкачать

Разложение на множители квадратного трехчлена
Квадратный трехчлен вида a x 2 + b x + c можно разложить на линейные множители. тогда получим, что a x 2 + b x + c = a ( x — x 1 ) ( x — x 2 ) , где x 1 и x 2 — это корни (комплексные или действительные).
Отсюда видно, что само разложение сводится к решению квадратного уравнения впоследствии.
Произвести разложение квадратного трехчлена на множители.
Необходимо найти корни уравнения 4 x 2 — 5 x + 1 = 0 . Для этого необходимо найти значение дискриминанта по формуле, тогда получим D = ( — 5 ) 2 — 4 · 4 · 1 = 9 . Отсюда имеем, что
x 1 = 5 — 9 2 · 4 = 1 4 x 2 = 5 + 9 2 · 4 = 1
Отсюда получаем, что 4 x 2 — 5 x + 1 = 4 x — 1 4 x — 1 .
Для выполнения проверки нужно раскрыть скобки. Тогда получим выражение вида:
4 x — 1 4 x — 1 = 4 x 2 — x — 1 4 x + 1 4 = 4 x 2 — 5 x + 1
После проверки приходим к исходному выражению. То есть можно сделать вывод, что разложение выполнено верно.
Произвести разложение на множители квадратный трехчлен вида 3 x 2 — 7 x — 11 .
Получим, что необходимо вычислить получившееся квадратное уравнение вида 3 x 2 — 7 x — 11 = 0 .
Чтобы найти корни, надо определить значение дискриминанта. Получим, что
3 x 2 — 7 x — 11 = 0 D = ( — 7 ) 2 — 4 · 3 · ( — 11 ) = 181 x 1 = 7 + D 2 · 3 = 7 + 181 6 x 2 = 7 — D 2 · 3 = 7 — 181 6
Отсюда получаем, что 3 x 2 — 7 x — 11 = 3 x — 7 + 181 6 x — 7 — 181 6 .
Произвести разложение многочлена 2 x 2 + 1 на множители.
Теперь нужно решить квадратное уравнение 2 x 2 + 1 = 0 и найти его корни. Получим, что
2 x 2 + 1 = 0 x 2 = — 1 2 x 1 = — 1 2 = 1 2 · i x 2 = — 1 2 = — 1 2 · i
Эти корни называют комплексно сопряженными, значит само разложение можно изобразить как 2 x 2 + 1 = 2 x — 1 2 · i x + 1 2 · i .
Произвести разложение квадратного трехчлена x 2 + 1 3 x + 1 .
Для начала необходимо решить квадратное уравнение вида x 2 + 1 3 x + 1 = 0 и найти его корни.
x 2 + 1 3 x + 1 = 0 D = 1 3 2 — 4 · 1 · 1 = — 35 9 x 1 = — 1 3 + D 2 · 1 = — 1 3 + 35 3 · i 2 = — 1 + 35 · i 6 = — 1 6 + 35 6 · i x 2 = — 1 3 — D 2 · 1 = — 1 3 — 35 3 · i 2 = — 1 — 35 · i 6 = — 1 6 — 35 6 · i
Получив корни, запишем
x 2 + 1 3 x + 1 = x — — 1 6 + 35 6 · i x — — 1 6 — 35 6 · i = = x + 1 6 — 35 6 · i x + 1 6 + 35 6 · i
Если значение дискриминанта отрицательное, то многочлены останутся многочленами второго порядка. Отсюда следует, что раскладывать их не будем на линейные множители.
Видео:8 класс, 35 урок, Уравнения высших степенейСкачать

Способы разложения на множители многочлена степени выше второй
При разложении предполагается универсальный метод. Большинство всех случаев основано на следствии из теоремы Безу. Для этого необходимо подбирать значение корня x 1 и понизить его степень при помощи деления на многочлена на 1 делением на ( x — x 1 ) . Полученный многочлен нуждается в нахождении корня x 2 , причем процесс поиска цикличен до тех пор, пока не получим полное разложение.
Если корень не нашли, тогда применяются другие способы разложения на множители: группировка, дополнительные слагаемые. Данная тема полагает решение уравнений с высшими степенями и целыми коэффициентами.
Видео:Алгебра 10 класс (Урок№12 - Решение алгебраических уравнений разложением на множители.)Скачать

Вынесение общего множителя за скобки
Рассмотрим случай, когда свободный член равняется нулю, тогда вид многочлена становится как P n ( x ) = a n x n + a n — 1 x n — 1 + . . . + a 1 x .
Видно, что корень такого многочлена будет равняться x 1 = 0 , тогда можно представить многочлен в виде выражения P n ( x ) = a n x n + a n — 1 x n — 1 + . . . + a 1 x = = x ( a n x n — 1 + a n — 1 x n — 2 + . . . + a 1 )
Данный способ считается вынесением общего множителя за скобки.
Выполнить разложение многочлена третьей степени 4 x 3 + 8 x 2 — x на множители.
Видим, что x 1 = 0 — это корень заданного многочлена, тогда можно произвести вынесение х за скобки всего выражения. Получаем:
4 x 3 + 8 x 2 — x = x ( 4 x 2 + 8 x — 1 )
Переходим к нахождению корней квадратного трехчлена 4 x 2 + 8 x — 1 . Найдем дискриминант и корни:
D = 8 2 — 4 · 4 · ( — 1 ) = 80 x 1 = — 8 + D 2 · 4 = — 1 + 5 2 x 2 = — 8 — D 2 · 4 = — 1 — 5 2
Тогда следует, что
4 x 3 + 8 x 2 — x = x 4 x 2 + 8 x — 1 = = 4 x x — — 1 + 5 2 x — — 1 — 5 2 = = 4 x x + 1 — 5 2 x + 1 + 5 2
Видео:Метод группировки и метод деления уголком при решении уравнений высших степеней.Скачать

Разложение на множители многочлена с рациональными корнями
Для начала примем за рассмотрение способ разложения, содержащий целые коэффициенты вида P n ( x ) = x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 , где коэффициента при старшей степени равняется 1 .
Когда многочлен имеет целые корни, тогда их считают делителями свободного члена.
Произвести разложение выражения f ( x ) = x 4 + 3 x 3 — x 2 — 9 x — 18 .
Рассмотрим, имеются ли целые корни. Необходимо выписать делители числа — 18 . Получим, что ± 1 , ± 2 , ± 3 , ± 6 , ± 9 , ± 18 . Отсюда следует, что данный многочлен имеет целые корни. Можно провести проверку по схеме Горнера. Она очень удобная и позволяет быстро получить коэффициенты разложения многочлена:
| x i | Коэффициенты многочленов | ||||
| 1 | 3 | — 1 | — 9 | — 18 | |
| 1 | 1 | 3 + 1 · 1 = 4 | — 1 + 4 · 1 = 3 | — 9 + 3 · 1 = — 6 | — 18 + ( — 6 ) · 1 = — 24 |
| — 1 | 1 | 3 + 1 · ( — 1 ) = 2 | — 1 + 2 · ( — 1 ) = — 3 | — 9 + ( — 3 ) · ( — 1 ) = — 6 | — 18 + ( — 6 ) · ( — 1 ) = — 12 |
| 2 | 1 | 3 + 1 · 2 = 5 | — 1 + 5 · 2 = 9 | — 9 + 9 · 2 = 9 | — 18 + 9 · 2 = 0 |
| 2 | 1 | 5 + 1 · 2 = 7 | 9 + 7 · 2 = 23 | 9 + 23 · 2 = 55 | |
| — 2 | 1 | 5 + 1 · ( — 2 ) = 3 | 9 + 3 · ( — 2 ) = 3 | 9 + 3 · ( — 2 ) = 3 | |
| 3 | 1 | 5 + 1 · 3 = 8 | 9 + 8 · 3 = 33 | 9 + 33 · 3 = 108 | |
| — 3 | 1 | 5 + 1 · ( — 3 ) = 2 | 9 + 2 · ( — 3 ) = 3 | 9 + 3 · ( — 3 ) = 0 | |
Отсюда следует, что х = 2 и х = — 3 – это корни исходного многочлена, который можно представить как произведение вида:
f ( x ) = x 4 + 3 x 3 — x 2 — 9 x — 18 = ( x — 2 ) ( x 3 + 5 x 2 + 9 x + 9 ) = = ( x — 2 ) ( x + 3 ) ( x 2 + 2 x + 3 )
Переходим к разложению квадратного трехчлена вида x 2 + 2 x + 3 .
Так как дискриминант получаем отрицательный, значит, действительных корней нет.
Ответ: f ( x ) = x 4 + 3 x 3 — x 2 — 9 x — 18 = ( x — 2 ) ( x + 3 ) ( x 2 + 2 x + 3 )
Допускается использование подбором корня и деление многочлена на многочлен вместо схемы Горнера. Перейдем к рассмотрению разложения многочлена, содержащим целые коэффициенты вида P n ( x ) = x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 , старший из которых на равняется единице.
Этот случай имеет место быть для дробно-рациональных дробей.
Произвести разложение на множители f ( x ) = 2 x 3 + 19 x 2 + 41 x + 15 .
Необходимо выполнить замену переменной y = 2 x , следует переходить к многочлену с коэффициентами равными 1 при старшей степени. Необходимо начать с умножения выражения на 4 . Получаем, что
4 f ( x ) = 2 3 · x 3 + 19 · 2 2 · x 2 + 82 · 2 · x + 60 = = y 3 + 19 y 2 + 82 y + 60 = g ( y )
Когда получившаяся функция вида g ( y ) = y 3 + 19 y 2 + 82 y + 60 имеет целые корни, тогда их нахождение среди делителей свободного члена. Запись примет вид:
± 1 , ± 2 , ± 3 , ± 4 , ± 5 , ± 6 , ± 10 , ± 12 , ± 15 , ± 20 , ± 30 , ± 60
Перейдем к вычислению функции g ( y ) в этих точка для того, чтобы получить в результате ноль. Получаем, что
g ( 1 ) = 1 3 + 19 · 1 2 + 82 · 1 + 60 = 162 g ( — 1 ) = ( — 1 ) 3 + 19 · ( — 1 ) 2 + 82 · ( — 1 ) + 60 = — 4 g ( 2 ) = 2 3 + 19 · 2 2 + 82 · 2 + 60 = 308 g ( — 2 ) = ( — 2 ) 3 + 19 · ( — 2 ) 2 + 82 · ( — 2 ) + 60 = — 36 g ( 3 ) = 3 3 + 19 · 3 2 + 82 · 3 + 60 = 504 g ( — 3 ) = ( — 3 ) 3 + 19 · ( — 3 ) 2 + 82 · ( — 3 ) + 60 = — 42 g ( 4 ) = 4 3 + 19 · 4 2 + 82 · 4 + 60 = 756 g ( — 4 ) = ( — 4 ) 3 + 19 · ( — 4 ) 2 + 82 · ( — 4 ) + 60 = — 28 g ( 5 ) = 5 3 + 19 · 5 2 + 82 · 5 + 60 = 1070 g ( — 5 ) = ( — 5 ) 3 + 19 · ( — 5 ) 2 + 82 · ( — 5 ) + 60
Получаем, что у = — 5 – это корень уравнения вида y 3 + 19 y 2 + 82 y + 60 , значит, x = y 2 = — 5 2 — это корень исходной функции.
Необходимо произвести деление столбиком 2 x 3 + 19 x 2 + 41 x + 15 на x + 5 2 .
Запишем и получим:
2 x 3 + 19 x 2 + 41 x + 15 = x + 5 2 ( 2 x 2 + 14 x + 6 ) = = 2 x + 5 2 ( x 2 + 7 x + 3 )
Проверка делителей займет много времени, поэтому выгодней предпринять разложение на множители полученного квадратного трехчлена вида x 2 + 7 x + 3 . Приравниванием к нулю и находим дискриминант.
x 2 + 7 x + 3 = 0 D = 7 2 — 4 · 1 · 3 = 37 x 1 = — 7 + 37 2 x 2 = — 7 — 37 2 ⇒ x 2 + 7 x + 3 = x + 7 2 — 37 2 x + 7 2 + 37 2
Отсюда следует, что
2 x 3 + 19 x 2 + 41 x + 15 = 2 x + 5 2 x 2 + 7 x + 3 = = 2 x + 5 2 x + 7 2 — 37 2 x + 7 2 + 37 2
Видео:✓ Теорема Безу. Рациональные нули многочленов | Ботай со мной #119 | Борис ТрушинСкачать

Искусственные приемы при разложении многочлена на множители
Рациональные корни не присущи всем многочленам. Для этого необходимо пользоваться специальными способами для нахождения множителей. Но не все многочлены можно разложить или представить в виде произведения.
Видео:Теорема Безу и разложение многочлена на множителиСкачать

Способ группировки
Бывают случаи, когда можно сгруппировывать слагаемые многочлена для нахождения общего множителя и вынесения его за скобки.
Произвести разложение многочлена x 4 + 4 x 3 — x 2 — 8 x — 2 на множители.
Потому как коэффициенты – целые числа, тогда корни предположительно тоже могут быть целыми. Для проверки возьмем значения 1 , — 1 , 2 и — 2 для того, чтобы вычислить значение многочлена в этих точках. Получаем, что
1 4 + 4 · 1 3 — 1 2 — 8 · 1 — 2 = — 6 ≠ 0 ( — 1 ) 4 + 4 · ( — 1 ) 3 — ( — 1 ) 2 — 8 · ( — 1 ) — 2 = 2 ≠ 0 2 4 + 4 · 2 3 — 2 2 — 8 · 2 — 2 = 26 ≠ 0 ( — 2 ) 4 + 4 · ( — 2 ) 3 — ( — 2 ) 2 — 8 · ( — 2 ) — 2 = — 6 ≠ 0
Отсюда видно, что корней нет, необходимо использовать другой способ разложения и решения.
Необходимо провести группировку:
x 4 + 4 x 3 — x 2 — 8 x — 2 = x 4 + 4 x 3 — 2 x 2 + x 2 — 8 x — 2 = = ( x 4 — 2 x 2 ) + ( 4 x 3 — 8 x ) + x 2 — 2 = = x 2 ( x 2 — 2 ) + 4 x ( x 2 — 2 ) + x 2 — 2 = = ( x 2 — 2 ) ( x 2 + 4 x + 1 )
После группировки исходного многочлена необходимо представить его как произведение двух квадратных трехчленов. Для этого нам понадобится произвести разложение на множители. получаем, что
x 2 — 2 = 0 x 2 = 2 x 1 = 2 x 2 = — 2 ⇒ x 2 — 2 = x — 2 x + 2 x 2 + 4 x + 1 = 0 D = 4 2 — 4 · 1 · 1 = 12 x 1 = — 4 — D 2 · 1 = — 2 — 3 x 2 = — 4 — D 2 · 1 = — 2 — 3 ⇒ x 2 + 4 x + 1 = x + 2 — 3 x + 2 + 3
x 4 + 4 x 3 — x 2 — 8 x — 2 = x 2 — 2 x 2 + 4 x + 1 = = x — 2 x + 2 x + 2 — 3 x + 2 + 3
Простота группировки не говорит о том, что выбрать слагаемы достаточно легко. Определенного способа решения не существует, поэтому необходимо пользоваться специальными теоремами и правилами.
Произвести разложение на множители многочлен x 4 + 3 x 3 — x 2 — 4 x + 2 .
Заданный многочлен не имеет целых корней. Следует произвести группировку слагаемых. Получаем, что
x 4 + 3 x 3 — x 2 — 4 x + 2 = = ( x 4 + x 3 ) + ( 2 x 3 + 2 x 2 ) + ( — 2 x 2 — 2 x ) — x 2 — 2 x + 2 = = x 2 ( x 2 + x ) + 2 x ( x 2 + x ) — 2 ( x 2 + x ) — ( x 2 + 2 x — 2 ) = = ( x 2 + x ) ( x 2 + 2 x — 2 ) — ( x 2 + 2 x — 2 ) = ( x 2 + x — 1 ) ( x 2 + 2 x — 2 )
После разложения на множители получим, что
x 4 + 3 x 3 — x 2 — 4 x + 2 = x 2 + x — 1 x 2 + 2 x — 2 = = x + 1 + 3 x + 1 — 3 x + 1 2 + 5 2 x + 1 2 — 5 2
Видео:Уравнения высших степеней 1 часть (старший коэффициент равен 1)Скачать

Использование формул сокращенного умножения и бинома Ньютона для разложения многочлена на множители
Внешний вид зачастую не всегда дает понять, каким способом необходимо воспользоваться при разложении. После того, как были произведены преобразования, можно выстроить строчку, состоящую из треугольника Паскаля, иначе их называют биномом Ньютона.
Произвести разложение многочлена x 4 + 4 x 3 + 6 x 2 + 4 x — 2 на множители.
Необходимо выполнить преобразование выражения к виду
x 4 + 4 x 3 + 6 x 2 + 4 x — 2 = x 4 + 4 x 3 + 6 x 2 + 4 x + 1 — 3
На последовательность коэффициентов суммы в скобках указывает выражение x + 1 4 .
Значит, имеем x 4 + 4 x 3 + 6 x 2 + 4 x — 2 = x 4 + 4 x 3 + 6 x 2 + 4 x + 1 — 3 = x + 1 4 — 3 .
После применения разности квадратов, получим
x 4 + 4 x 3 + 6 x 2 + 4 x — 2 = x 4 + 4 x 3 + 6 x 2 + 4 x + 1 — 3 = x + 1 4 — 3 = = x + 1 4 — 3 = x + 1 2 — 3 x + 1 2 + 3
Рассмотрим выражение, которое находится во второй скобке. Понятно, что там коней нет, поэтому следует применить формулу разности квадратов еще раз. Получаем выражение вида
x 4 + 4 x 3 + 6 x 2 + 4 x — 2 = x 4 + 4 x 3 + 6 x 2 + 4 x + 1 — 3 = x + 1 4 — 3 = = x + 1 4 — 3 = x + 1 2 — 3 x + 1 2 + 3 = = x + 1 — 3 4 x + 1 + 3 4 x 2 + 2 x + 1 + 3
Произвести разложение на множители x 3 + 6 x 2 + 12 x + 6 .
Займемся преобразованием выражения. Получаем, что
x 3 + 6 x 2 + 12 x + 6 = x 3 + 3 · 2 · x 2 + 3 · 2 2 · x + 2 3 — 2 = ( x + 2 ) 3 — 2
Необходимо применить формулу сокращенного умножения разности кубов. Получаем:
x 3 + 6 x 2 + 12 x + 6 = = ( x + 2 ) 3 — 2 = = x + 2 — 2 3 x + 2 2 + 2 3 x + 2 + 4 3 = = x + 2 — 2 3 x 2 + x 2 + 2 3 + 4 + 2 2 3 + 4 3
Видео:Метод неопределенных коэффициентовСкачать

Способ замены переменной при разложении многочлена на множители
При замене переменной производится понижение степени и разложение многочлена на множители.
Произвести разложение на множители многочлена вида x 6 + 5 x 3 + 6 .
По условию видно, что необходимо произвести замену y = x 3 . Получаем:
x 6 + 5 x 3 + 6 = y = x 3 = y 2 + 5 y + 6
Корни полученного квадратного уравнения равны y = — 2 и y = — 3 , тогда
x 6 + 5 x 3 + 6 = y = x 3 = y 2 + 5 y + 6 = = y + 2 y + 3 = x 3 + 2 x 3 + 3
Необходимо применить формулу сокращенного умножения суммы кубов. Получим выражения вида:
x 6 + 5 x 3 + 6 = y = x 3 = y 2 + 5 y + 6 = = y + 2 y + 3 = x 3 + 2 x 3 + 3 = = x + 2 3 x 2 — 2 3 x + 4 3 x + 3 3 x 2 — 3 3 x + 9 3
То есть получили искомое разложение.
Рассмотренные выше случаи помогут в рассмотрении и разложении многочлена на множители разными способами.
📽️ Видео
Теорема Виета для уравнений высших степеней. Рациональные уравнения Часть 4 из 4Скачать

Схема ГорнераСкачать

КАК РЕШАТЬ КУБИЧЕСКИЕ УРАВНЕНИЯ | Разбираем на конкретном примереСкачать

Решение уравнений высших степеней: метод группировкиСкачать

Теорема Безу. 10 класс.Скачать

Уравнения высших степеней. Решение уравнений с помощью деления в столбикСкачать