- Правила ввода функции
- Достаточные условия сходимости метода итерации
- Решение трансцендентных уравнений методом простых итераций
- Практическая работа 5 по теме «Решение алгебраических и трансцендентных уравнений приближенными методами ( метод итераций)»
- Просмотр содержимого документа «Практическая работа 5 по теме «Решение алгебраических и трансцендентных уравнений приближенными методами ( метод итераций)»»
- 🔥 Видео
Правила ввода функции
- Примеры
≡ x^2/(1+x)
cos 2 (2x+π) ≡ (cos(2*x+pi))^2≡ x+(x-1)^(2/3)
На рис.1а, 1б в окрестности корня |φ′(x)| 1, то процесс итерации может быть расходящимся (см. рис.2).
Видео:Метод простой итерации Пример РешенияСкачать

Достаточные условия сходимости метода итерации
Процесс нахождения нулей функции методом итераций состоит из следующих этапов:
- Получить шаблон с омощью этого сервиса.
- Уточнить интервалы в ячейках B2 , B3 .
- Копировать строки итераций до требуемой точности (столбец D ).
Примечание: столбец A — номер итерации, столбец B — корень уравнения X , столбец C — значение функции F(X) , столбец D — точность eps .
Видео:Метод простых итераций пример решения нелинейных уравненийСкачать

Решение трансцендентных уравнений методом простых итераций
Исходное уравнение (3.1) преобразуем к эквивалентному уравнению:
x =  (x). (x). | (3.8) |
Пусть известно начальное приближение (полученное, например, на этапе отделения корней): x = x 0. Подставим его в правую часть (3.8) и получим новое приближение: x1 = 
xk = 
В качестве условия окончания вычислительного процесса можно взять выполнение неравенства: ½xk — xk-1½ * — истинное, искомое значение корня; x0 — начальное приближение к корню; x1, x2, x3 — очередные итерации.
 Рис.3.8. Рис.3.8. |  Рис.3.9. Рис.3.9. |
При использовании этого метода возникает вопрос о его сходимости. Дело в том, что при некоторых условиях расстояние между истинным корнем и приближениями к нему может возрастать с каждой новой итерацией, как это показано на рис.3.10, 3.11.
 Рис.3.10. Рис.3.10. | 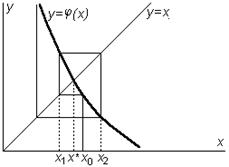 Рис.3.11. Рис.3.11. |
Условием сходимости метода простых итераций является выполнение в окрестности искомого корня неравенства:
½  (x)½ . F(x) = 0 (x)½ . F(x) = 0 | Þ | C . F(x) + x = x | (3.15) |
Здесь C — некоторый параметр, выбираемый из условия сходимости процесса.
При использовании преобразования (3.15) условием окончания вычислительного процесса является выполнение неравенства


В программе необходимо указывать функцию F(x) и вводить вычисленный заранее параметрС и значение допустимой погрешности 
Видео:Решение нелинейного уравнения методом простых итераций (программа)Скачать

Практическая работа 5 по теме «Решение алгебраических и трансцендентных уравнений приближенными методами ( метод итераций)»
Тема: Решение алгебраических и трансцендентных уравнений приближенными методами ( метод итераций)
Просмотр содержимого документа
«Практическая работа 5 по теме «Решение алгебраических и трансцендентных уравнений приближенными методами ( метод итераций)»»
Цель: Освоить численные методы, используемые при решении алгебраических и трансцендентных уравнений
— способы решения алгебраических и трансцендентных уравнений приближенными методами;
— находить приближенное значение корней алгебраических и трансцендентных уравнений;
— составлять алгоритмы и программы для нахождения приближенных решений алгебраических и трансцендентных уравнений.
Форма организации занятия – индивидуальная.
Итерация (лат) Повторное применение какой-либо математической операции.
Заменим уравнение F(x) = 0 равносильным уравнением х = f(x).
Пусть ξ – корень уравнения х = f(x), а х0, полученное каким-либо способом нулевое приближение к корню ξ. Подставляя х0 в правую часть уравнения х = f(x), получим некоторое число х1 = f(x0). Повторим данную процедуру с х1 и получим х2 = f(x1), Повторяя описанную процедуру, получим последовательность: х0, х1, х2……хn…… , называемую итерационной последовательностью.
Геометрическая интерпретация данного алгоритма:

Итерационная последовательность может быть как сходящейся, так и расходящейся, что определяется видом функции f(x).
У сходящейся последовательности существует конечный предел.
Теорема 1: Если функция f(x) непрерывна, а последовательность х0, х1, х2……хn…… сходится, то предел последовательности х0, х1, х2……хn…… является корнем уравнения х = f(x).

Найдем предел xn
Условие сходимости итерационного процесса определяется теоремой о достаточном условии сходимости итерационного процесса.
Теорема 2: Пусть х = f(x) имеет единственный корень на отрезке [a,b] и выполнены условия:
f(x) определена и дифференцируема на [a,b].
Существует такое вещественное q , что 

Тогда итерационная последовательность xn=f(xn-1) (n=1,2…..) сходится при любом начальном приближении
Оценка погрешности метода простой итерации:
Пусть xn — приближение к истинному значению корня уравнения х = f(x).
Абсолютная ошибка приближения xn оценивается
Отсюда можно вывести: Δ xn
При заданной точности ответа ε итерационный процесс прекращается, если Δ xn ≤ ε.
Метод итераций для решения уравнений типа 
что сначала отделяется корень уравнения,
затем оно преобразуется к виду x = φ(x). с правой частью, имеющей производную по модулю меньшую, чем 1, на всем отрезке, отделяющем корень, Этот переход можно осуществить разными способами, в зависимости от вида f(x). Например, можно положить φ(x) = x + bf(x), где b = const
Процесс построения последовательности надо прервать тогда, когда два раза подряд получится одно и то же число с заданной степенью точности.
Наиболее простой критерий окончания процесса 
Пример №5. Методом итераций уточнить корень уравнения 
Уравнение F(x)=0 приведем к виду 
1) 
Определим, какой из полученных функций следует воспользоваться для вычисления последовательных приближений. Итерационный процесс сходится, если
Выберем на отрезке [0; 1] произвольную точку x0. Пусть x0=0,5. Тогда
Проверим условие сходимости итерационного процесса:
— расходящийся итерационный процесс;
— сходящийся итерационный процесс.
Следовательно, для вычисления последовательных приближений можно использовать только
хк+1= . В качестве начального значения выберем середину отрезка [0; 1].
🔥 Видео
Решение слау методом итераций. Метод простых итераций c++.Скачать

10 Численные методы решения нелинейных уравненийСкачать

Алгоритмы С#. Метод простых итерацийСкачать

Метод итерацийСкачать

1 3 Решение нелинейных уравнений методом простых итерацийСкачать

Метод Ньютона (метод касательных) Пример РешенияСкачать

2.2 Итерационные методы решения СЛАУ (Якоби, Зейделя, релаксации)Скачать

Метод итераций (последовательных приближений)Скачать

Решение системы линейных уравнений методом итерацийСкачать

8 Метод простой итерации Ручной счет Решение системы линейных уравнений СЛАУСкачать

4.2 Решение систем нелинейных уравнений. МетодыСкачать

Решение систем линейных уравнений методом простой итерации в ExcelСкачать

Метод простых итераций - PascalСкачать

Метод половинного деления решение нелинейного уравненияСкачать

Метод половинного деления. ДихотомияСкачать

Отделение корней уравнений аналитическим методом. Уточнение корней методом половинного деленияСкачать

Решение систем линейных уравнений, урок 5/5. Итерационные методыСкачать

 ≡ x^2/(1+x)
≡ x^2/(1+x) 






