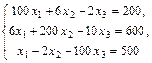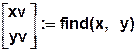Метод простых итераций для системы уравнений матлаб (8 видео)

Решение систем нелинейных уравнений в Matlab

Доброго времени суток! В этой статье мы поговорим о решении систем нелинейных алгебраических уравнений в Matlab. Вслед за решением нелинейных уравнений, переходим к их системам, рассмотрим несколько методов реализации в Matlab.

Содержание

Общая информация
Оператор Matlab для решения СНАУ
Метод простых итераций в Matlab для решения СНАУ
Метод Ньютона в Matlab для решения СНАУ
Заключение
Метод простых итераций
Программная реализация метода простой итерации для решения СЛАУ в пакете MATLAB
📸 Видео

Общая информация

Итак, в прошлой статье мы рассмотрели нелинейные уравнения и теперь необходимо решить системы таких уравнений. Система представляет собой набор нелинейных уравнений (их может быть два или более), для которых иногда возможно найти решение, которое будет подходить ко всем уравнениям в системе.

В стандартном виде, количество неизвестных переменных равно количеству уравнений в системе. Необходимо найти набор неизвестных переменных, которые при подставлении в уравнения будут приближать значение уравнения к 0. Иногда таких наборов может быть несколько, даже бесконечно много, а иногда решений не существует.

Чтобы решить СНАУ, необходимо воспользоваться итеративными методами. Это методы, которые за определенное количество шагов получают решение с определенной точностью. Также очень важно при решении задать достаточно близкое начальное приближение, то есть такой набор переменных, которые близки к решению. Если решается система из 2 уравнений, то приближение находится с помощью построение графика двух функций.

Далее, мы рассмотрим стандартный оператор Matlab для решения систем нелинейных алгебраических уравнений, а также напишем метод простых итераций и метод Ньютона.

Оператор Matlab для решения СНАУ

В среде Matlab существует оператор fsolve, который позволяет решить систему нелинейных уравнений. Сразу рассмотрим задачу, которую, забегая вперед, решим и другими методами для проверки.

Решить систему нелинейных уравнений с точность 10 -2 :
cos(x-1) + y = 0.5
x-cos(y) = 3

Нам дана система из 2 нелинейных уравнений и сначала лучше всего построить график. Воспользуемся командой ezplot в Matlab, только не забудем преобразовать уравнения к стандартному виду, где правая часть равна 0:

Функция ezplot строит график, принимая символьную запись уравнения, а для задания цвета и толщины линии воспользуемся функцией set. Посмотрим на вывод:

Как видно из графика, есть одно пересечение функций — то есть одно единственное решение данной системы нелинейных уравнений. И, как было сказано, по графику найдем приближение. Возьмем его как (3.0, 1.0). Теперь найдем решение с его помощью:

Создадим функцию m-файлом fun.m и поместим туда следующий код:

Заметьте, что эта функция принимает вектор приближений и возвращает вектор значений функции. То есть, вместо x здесь x(1), а вместо y — x(2). Это необходимо, потому что fsolve работает с векторами, а не с отдельными переменными.

И наконец, допишем функцию fsolve к коду построения графика таким образом:

Таким образом у нас образуется два m-файла. Первый строит график и вызывает функцию fsolve, а второй необходим для расчета самих значений функций. Если вы что-то не поняли, то в конце статьи будут исходники.

И в конце, приведем результаты:

xr (это вектор решений) =
3.3559 1.2069

fr (это значения функций при таких xr, они должны быть близки к 0) =
1.0e-09 *
0.5420 0.6829

ex (параметр сходимости, если он равен 1, то все сошлось) =
1

И, как же без графика с ответом:

Метод простых итераций в Matlab для решения СНАУ

Теперь переходим к методам, которые запрограммируем сами. Первый из них — метод простых итераций. Он заключается в том, что итеративно приближается к решению, конечно же, с заданной точностью. Алгоритм метода достаточно прост:

Если возможно, строим график.
Из каждого уравнения выражаем неизвестную переменную след. образом: из 1 уравнения выражаем x1, из второго — x2, и т.д.
Выбираем начальное приближение X0, например (3.0 1.0)
Рассчитываем значение x1, x2. xn, которые получили на шаге 2, подставив значения из приближения X0.
Проверяем условие сходимости, (X-X0) должно быть меньше точности
Если 5 пункт не выполнился, то повторяем 4 пункт.

И перейдем к практике, тут станет все понятнее.
Решить систему нелинейных уравнений методом простых итераций с точность 10 -2 :
cos(x-1) + y = 0.5
x-cos(y) = 3

График мы уже строили в предыдущем пункте, поэтому переходим к преобразованию. Увидим, что x из первого уравнения выразить сложно, поэтому поменяем местами уравнения, это не повлияет на решение:

x-cos(y) = 3
cos(x-1) + y = 0.5

Далее приведем код в Matlab:

В этой части мы выразили x1 и x2 (у нас это ‘x’ и ‘y’) и задали точность.

В этой части в цикле выполняются пункты 4-6. То есть итеративно меняются значения x и y, пока отличия от предыдущего значения не станет меньше заданной точности.

k = 10
x = 3.3587
y = 1.2088

Как видно, результаты немного отличаются от предыдущего пункта. Это связано с заданной точностью, можете попробовать поменять точность и увидите, что результаты станут такими же, как и при решении стандартным методом Matlab.

Метод Ньютона в Matlab для решения СНАУ

Решение систем нелинейных уравнений в Matlab методом Ньютона является более эффективным, чем использование метода простых итераций. Сразу же представим алгоритм, а затем перейдем к реализации.

Если возможно, строим график.
Выбираем начальное приближение X0, например (3.0 1.0)
Рассчитываем матрицу Якоби w, это матрица частных производных каждого уравнения, считаем ее определитель для X0.
Находим вектор приращений, который рассчитывается как dx = -w -1 * f(X0)
Находим вектор решения X = X0 + dx
Проверяем условие сходимости, (X-X0) должно быть меньше точности

Далее, решим тот же пример, что и в предыдущих пунктах. Его график мы уже строили и начальное приближение останется таким же.
Решить систему нелинейных уравнений методом Ньютона с точность 10 -2 :
cos(x-1) + y = 0.5
x-cos(y) = 3

Перейдем к коду:

Сначала зададим начальное приближение. Затем необходимо просчитать матрицу Якоби, то есть частные производные по всем переменным. Воспользуемся символьным дифференцированием в Matlab, а именно командой diff с использованием символьных переменных.

Далее, сделаем первую итерацию метода, чтобы получить вектор выходных значений X, а потом уже сравнивать его с приближением в цикле.

В этой части кода выполняем первую итерацию, чтобы получить вектор решения и сравнивать его с вектором начального приближения. Отметим, чтобы посчитать значение символьной функции в Matlab, необходимо воспользоваться функцией subs. Эта функция заменяет переменную на числовое значение. Затем функция double рассчитает это числовое значение.

Все действия, которые были выполнены для расчета производных, на самом деле можно было не производить, а сразу же задать производные. Именно так мы и поступим в цикле.

В этой части кода выполняется цикл по расчету решения с заданной точностью. Еще раз отметим, что если в первой итерации до цикла были использованы функции diff, double и subs для вычисления производной в Matlab, то в самом цикле матрица якоби была явно задана этими частными производными. Это сделано, чтобы показать возможности среды Matlab.

За 3 итерации достигнут правильный результат. Также важно сказать, что иногда такие методы могут зацикливаться и не закончить расчеты. Чтобы такого не было, мы прописали проверку на количество итераций и запретили выполнение более 100 итераций.

Заключение

В этой статье мы познакомились с основными понятиями систем нелинейных алгебраических уравнений в Matlab. Рассмотрели несколько вариантов их решения, как стандартными операторами Matlab, так и запрограммированными методами простых итераций и Ньютона.

Видео:Метод простых итераций пример решения нелинейных уравненийСкачать

Метод простых итераций

Дата добавления: 2015-07-23 ; просмотров: 7352 ; Нарушение авторских прав

Лабораторная работа №5

Тема: Решение СЛАУ итерационным методом в MathCAD.

Цель: изучение приемов численного решения систем линейных уравнений с помощью функций MathCAD.

Порядок выполнения работы

1. Ознакомиться с теоретическими положениями.

2. Рассмотреть пример решения СЛАУ итерационным методом в MathCAD.

3. Выполнить практическое задание.

4. Ответить на контрольные вопросы.

Содержание отчета

1. Тема, цель работы.

2. Практическое задание:

2.1. Постановка задачи.

2.2. Результаты выполнения.

3. Ответы на контрольные вопросы.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Итерационные методы – это методы, позволяющие получить решение системы с заданной точностью путем сходящихся итерационных процессов (метод итерации, метод Зейделя и др.).

Вследствие неизбежных округлений результаты даже точных методов являются приближенными. При использовании итерационных методов, сверх того, добавляется погрешность метода.

Эффективное применение итерационных методов существенно зависит от удачного выбора начального приближения и быстроты сходимости процесса.

Метод простых итераций

Пусть дана линейная система (1).

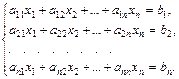(1)

Систему (1) коротко можно записать в виде матричного уравнения:

Ах = b,

(2)

Предполагая, что диагональные коэффициенты

разрешим первое уравнение системы (1) относительно х₁, второе – относительно х₂ и т. д. Тогда получим эквивалентную систему

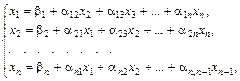(3)

при i ¹ j

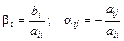
Систему (3) можно записать в матричной форме

x = b + ax,

а любое (k + 1) приближение вычисляется по формуле

x (k+1) = b + ax (k) .

(4)

Напишем формулы приближений в развернутом виде:

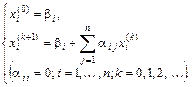(4¢)

Приведем достаточное условие сходимости метода итераций.

Теорема:Процесс итерации для приведенной линейной системы (18) сходится к единственному ее решению, если какая-нибудь каноническая норма матрицы a меньше единицы, т.е. для итерационного процесса (19) достаточное условие есть

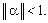(5)

Следствие 1. Процесс итерации для системы (3) сходится, если:

1) (k +1) .

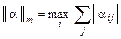
Пример решения СЛАУ итерационным методом в MathCAD.

Решить систему методом простых итераций:

Результат на экране:

\|	следующая лекция ==>
Контрольные задания	\|

Не нашли то, что искали? Google вам в помощь!

Видео:Метод простой итерации Пример РешенияСкачать

Программная реализация метода простой итерации для решения СЛАУ в пакете MATLAB

Входные параметры: U – расширенная матрица коэффициентов, eps – требуемая точность решения.

Function res = Jakobi(U,eps);

error (‘Неверно задана система’);

%приведение системы к диагонально доминирующему виду

error(‘Система не совместна’);

%сумма по строкам

if k 1) && (max_norm2>1) && (max_norm3>1))

error(‘Введенная матрица не является диагонально преобладающей’)

%нахождение суммы для Х1(i)

sum = sum + ( A(i,j) * X0(j) );

while ( abs( X0(i) — X1(i) ) > eps )

%нахождение суммы для Х1(i)

sum = sum + ( A(i,j) * X0(j) );

%вывод вектора решений

%вывод числа итераций для выполненияусловия точности

ВСТРОЕННЫЕ ФУНКЦИИ ПАКЕТОВ MATHCAD И MATLAB

ДЛЯ ПРИБЛИЖЕННОГО РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ

АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ

Пакет MATHCAD

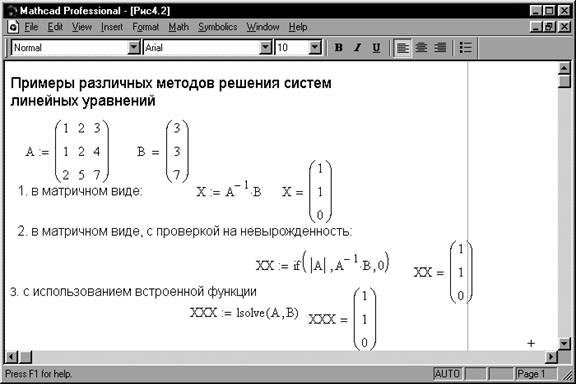
Решение систем линейных уравнений – довольно распространенная задача. Для системы линейных уравнений, заданной в матричном виде AX=B, вектор решения можно получить из очевидного выражения X=A-1B, или, например, из решения системы уравнений с проверкой на невырожденность матрицы:X:=if(|A|,A -1 B,0).

Следует обратить внимание на то, что пакет содержит и встроенную функцию решения линейных систем lsolve(A,B), где А– матрица коэффициентов, а В – вектор свободных членов. Пример использования предложенных методов показан на рис. 5.1.

Рис. 5.1. Примеры решения системы

Для решения систем уравнений, систем неравенств, смешанных систем служат решающие блоки. Структура решающего блока:

начало | Given

тело | несколько конструкций вида АВ1 оп АВ2

(оп – некоторая операция отношения, причём для написания знака равенства используется особый «жирный» знак равенства, который находится на панели инструментов; знак присваивания в теле решающего блока не используется)

конец | FIND (список) или MINERR (список).

Список – это перечень переменных, которые необходимо найти.

С помощью FIND ищут точное решение; если оно отсутствует, то возникает ошибка. Посредством MINERR всегда будет найдено решение, минимизирующее невязку ограничений. Переменная ERR– величина ошибки.

Перед решающим блоком необходимо задать начальные условия для всех искомых переменных, можно в векторном виде. Соответственно, в теле решающего блока можно использовать запись уравнений в матричном виде. Максимальное количество уравнений в системе доведено до двухсот. Часто приходится решать системы уравнений при наличии определенных ограничений. Таким образом, в теле решающего блока могут быть одновременно как равенства, так и неравенства. Пример такой системы приведен ниже:

Given

find (x,y) =

Для последующего использования результатов необходимо так организовать конец:

В теле решающего блока нельзя строить графики, выполнять вычисления.

Итерации производятся до тех пор, пока ôERRô£ TOL. Если встречается седловая точка и не известно, куда направлен градиент, то выдается сообщение not converging (не решаемо). Количество итераций ограничено. Возможно сообщение об ошибке вида did not find solution (не найдено решение).

При возникновении таких ошибок можно:

– изменить точность – TOL;

– заменить начальные условия;

– заменить find на minerr и получить приближенное решение.

Однако при использовании функций findи minerrнужно проявлять осторожность и обязательно предусматривать проверку решений, т.к. нередки случаи, когда решение может оказаться ошибочным.

Для получения другого решения можно поменять начальные условия, для уточнения – уменьшить TOL.

Пакет MATLAB

Рассмотрим две системы линейных уравнений: АХ=В и ХА=В. В MATLAB такие системы решаются без вычисления обратной матрицы. Два типа матричного деления / и используются для этих двух ситуаций, когда неизвестная матрица стоит слева или справа от матрицы коэффициентов:

Х=АВ соответствует решению АХ=В;

Х=В/А соответствует решению ХА = В.

При этом должны выполняться условия соответствия размерностей матриц X, А, В. Напомним, что для варианта Х=АВ матрица X должна иметь то же количество столбцов, что и матрица В, и то же число строк, сколько столбцов у матрицы А. Для Х=В/А эти условия обратны.

Алгебраические свойства оператора / можно вывести из соотношения(В/А)’ = (А’В’).

Матрица не обязательно должна быть квадратной, она может быть размером mхn. При этом существуют следующие варианты:

· m = n – квадратная система, возможно нахождение точного решения;

· m > n – переопределенная система, решение ищется с помощью метода наименьших квадратов;

· m n и ранг матрицы равен n, то каждое из трех следующих выражений вычисляет X по методу наименьших квадратов:

Х=АВ

Х=рinv(А)*В

Х=inv(А’*А)*А’*В

В противном случае решение Xпо методу наименьших квадратов не единственно и существует множество векторов, минимизирующих norm(A*X-B).Решение, вычисленное с помощью Х=АВ,– базовое решение, имеющее не больше r ненулевых компонент: r=rank(A). Решение, вычисленное с помощью Х=рinv(А)*В,– это решение с минимальной нормой X.