Доброго времени суток. В этой статье мы разберем решение простых нелинейных уравнений с помощью средств Matlab. Посмотрим в действии как стандартные функции, так и сами запрограммируем три распространенных метода для решения нелинейных уравнений.
- Общая информация
- Стандартные функции Matlab
- Метод перебора Matlab
- Метод простых итераций Matlab
- Метод половинного деления Matlab
- Заключение
- Решение систем нелинейных уравнений в Matlab
- Общая информация
- Оператор Matlab для решения СНАУ
- Метод простых итераций в Matlab для решения СНАУ
- Метод Ньютона в Matlab для решения СНАУ
- Заключение
- Как решить уравнение в matlab
- Решение нелинейных уравнений в Matlab
- Общая информация
- Стандартные функции Matlab
- Метод перебора Matlab
- Метод простых итераций Matlab
- Метод половинного деления Matlab
- Заключение
- Модуль-3-210700 / 2Дисциплина ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЕ ППП-210700 / Раздел-05-ППП-MatLab / Учебное пособие / Тема-05-02-MatLab
- solve
- Синтаксис
- Описание
- Примеры
- Решите квадратное уравнение
- Решите полином и возвратите действительные решения
- Численно решите уравнения
- Решите многомерные уравнения и присвойте Выходные параметры структуре
- Решите неравенства
- Решите многомерные уравнения и присвойте Выходные параметры переменным
- Используйте параметры и условия совершенствовать решение
- Сократите результат с правилами упрощения
- Проигнорируйте предположения на переменных
- Решите полиномиальные знатные уравнения
- Возвратите одно решение
- Входные параметры
- eqn — Уравнение, чтобы решить символьное выражение | символьное уравнение
- var — Переменная, для которой вы решаете уравнение символьная переменная
- eqns Система уравнений символьные выражения | символьные уравнения
- vars — Переменные, для которых вы решаете уравнение или систему уравнений символьный вектор | символьная матрица
- Аргументы name-value
- Real — Отметьте для возврата только действительных решений false (значение по умолчанию) | true
- ReturnConditions — Отметьте для возврата параметров и условий false (значение по умолчанию) | true
- IgnoreAnalyticConstraints — Правила упрощения применились к выражениям и уравнениям false (значение по умолчанию) | true
- IgnoreProperties — Отметьте для возврата решений, противоречивых со свойствами переменных false (значение по умолчанию) | true
- MaxDegree — Максимальная степень полиномиальных уравнений, для которых решатель использует явные формулы 2 (значение по умолчанию) | положительное целое число, меньшее, чем 5
- PrincipalValue — Отметьте для возврата одного решения false (значение по умолчанию) | true
- Выходные аргументы
- S — Решения уравнения символьный массив
- Y — Решения системы уравнений структура
- y1. yN — Решения системы уравнений символьные переменные
- parameters — Параметры в решении вектор из сгенерированных параметров
- conditions — Условия, при которых решения допустимы вектор из символьных выражений
- Советы
- Алгоритмы
- 🎦 Видео
Общая информация
Уравнения, которые содержат переменные, находящиеся в степенях, отличающихся от единицы, или имеющие нелинейные математические выражения (корень, экспонента, логарифм, синус, косинус и т.д.), а также имеющие вид f(x) = 0 называются нелинейными. В зависимости от сложности такого уравнения применяют методы для решения нелинейных уравнений.
В этой статье, помимо стандартных функций Matlab, мы рассмотрим следующие методы:
- Метод перебора
- Метод простых итераций
- Метод половинного деления
Рассмотрим коротко их алгоритмы и применим для решения конкретной задачи.
Стандартные функции Matlab
Для решения нелинейных уравнений в Matlab есть функция fzero. Она принимает в качестве аргументов саму функцию, которую решаем, и отрезок, на котором происходит поиск корней нелинейного уравнения.
И сразу же разберем пример:
Решить нелинейное уравнение x = exp(-x), предварительно определив интервалы, на которых существуют решения уравнения.
Итак, для начала следует привести уравнение к нужному виду: x — exp(-x) = 0 , а затем определить интервалы, в которых будем искать решение уравнения. Методов для определения интервалов множество, но так как пример достаточно прост мы воспользуемся графическим методом.
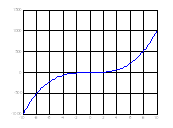
Здесь задали примерные границы по оси x, чтобы можно было построить график и посмотреть как ведет себя функция. Вот график: 
Из графика видно, что на отрезке [0;1] есть корень уравнения (там, где y = 0), соответственно в дальнейшем будем использовать этот интервал. Чем точнее выбран интервал, тем быстрее метод придет к решению уравнения, а для сложных уравнений правильный выбор интервала определяет погрешность, с которой будет получен ответ.
С помощью стандартной функции Matlab находим корень нелинейного уравнения и выводим. Теперь для проверки отобразим все это графически:
Как вы видите, все достаточно точно просчиталось. Теперь мы исследуем эту же функцию с помощью других методов и сравним полученные результаты.
Метод перебора Matlab
Самый простой метод, который заключается в том, что сначала задается какое то приближение x (желательно слева от предполагаемого корня) и значение шага h. Затем, пока выполняется условие f(x) * f(x + h) > 0, значение x увеличивается на значение шага x = x + h. Как только условие перестало выполняться — это значит, что решение нелинейного уравнения находится на интервале [x; x + h].
Теперь реализуем метод перебора в Matlab:
Лучше всего создать новый m-файл, в котором и прописать код. После вызова получаем такой вывод:
Функцию объявляем с помощью очень полезной команды inline, в цикле пока выполняется условие отсутствия корней (или их четного количества), прибавляем к x значение шага. Очевидно, что чем точнее начальное приближение, тем меньше итераций необходимо затратить.
Метод простых итераций Matlab
Этот метод заключается в том, что функцию преобразуют к виду: x = g(x). Эти преобразования можно сделать разными способами, в зависимости от вида начальной функции. Помимо этого следует задать интервал, в котором и будет производиться итерационный процесс, а также начальное приближение. Сам процесс строится по схеме xn= g(xn-1). То есть итерационно проходим от предыдущего значения к последующему.
Процесс заканчивается как только выполнится условие: , то есть, как только будет достигнута заданная точность. И сразу же разберем реализацию метода простых итераций в Matlab для примера, который был приведен выше.
Здесь должно быть все понятно, кроме одного: зачем задавать число итераций? Это нужно для того, чтобы программа не зацикливалась и не выполняла ненужные итерации, а также потому что не всегда программа может просчитать решение с нужной точностью — поэтому следует ограничивать число итераций.
А вот и вывод программы:
Очевидно, что метод простых итераций работает гораздо быстрее и получает точное решение.
Метод половинного деления Matlab
Метод достаточно прост: существует отрезок поиска решения [a;b], сначала находят значение функции в точке середины c, где c = (a+b)/2. Затем сравнивают знаки f(a) и f(c). Если знаки разные — то решение находится на отрезке [a;c], если нет — то решение находится на отрезке [c;b]. Таким образом мы сократили область в 2 раза. Такое сокращение происходит и дальше, пока не достигнем заданной точности.
Перейдем к реализации метода в Matlab:
Все самое важное происходит в цикле: последовательно сокращаем область нахождения решения, пока не будет достигнута заданная точность.
Вот что получилось в выводе:
Этот метод хорошо работает, когда правильно определен интервал, на котором находится решение. Тем не менее, метод простых итераций считается наиболее точным и быстрым.
Заключение
Сегодня мы рассмотрели решение нелинейных уравнений в Matlab. Теперь нам известны методы перебора, половинного деления, простых итераций. А также, когда нам не важно реализация метода, то можно использовать стандартную функцию в Matlab.
На этом все — спасибо за внимание. В следующей статье мы разберем решение систем нелинейных уравнений в matlab.
Видео:Метод простых итераций пример решения нелинейных уравненийСкачать

Решение систем нелинейных уравнений в Matlab
Доброго времени суток! В этой статье мы поговорим о решении систем нелинейных алгебраических уравнений в Matlab. Вслед за решением нелинейных уравнений, переходим к их системам, рассмотрим несколько методов реализации в Matlab.
Общая информация
Итак, в прошлой статье мы рассмотрели нелинейные уравнения и теперь необходимо решить системы таких уравнений. Система представляет собой набор нелинейных уравнений (их может быть два или более), для которых иногда возможно найти решение, которое будет подходить ко всем уравнениям в системе. 
В стандартном виде, количество неизвестных переменных равно количеству уравнений в системе. Необходимо найти набор неизвестных переменных, которые при подставлении в уравнения будут приближать значение уравнения к 0. Иногда таких наборов может быть несколько, даже бесконечно много, а иногда решений не существует.
Чтобы решить СНАУ, необходимо воспользоваться итеративными методами. Это методы, которые за определенное количество шагов получают решение с определенной точностью. Также очень важно при решении задать достаточно близкое начальное приближение, то есть такой набор переменных, которые близки к решению. Если решается система из 2 уравнений, то приближение находится с помощью построение графика двух функций.
Далее, мы рассмотрим стандартный оператор Matlab для решения систем нелинейных алгебраических уравнений, а также напишем метод простых итераций и метод Ньютона.
Оператор Matlab для решения СНАУ
В среде Matlab существует оператор fsolve, который позволяет решить систему нелинейных уравнений. Сразу рассмотрим задачу, которую, забегая вперед, решим и другими методами для проверки.
Решить систему нелинейных уравнений с точность 10 -2 :
cos(x-1) + y = 0.5
x-cos(y) = 3
Нам дана система из 2 нелинейных уравнений и сначала лучше всего построить график. Воспользуемся командой ezplot в Matlab, только не забудем преобразовать уравнения к стандартному виду, где правая часть равна 0:
Функция ezplot строит график, принимая символьную запись уравнения, а для задания цвета и толщины линии воспользуемся функцией set. Посмотрим на вывод:
Как видно из графика, есть одно пересечение функций — то есть одно единственное решение данной системы нелинейных уравнений. И, как было сказано, по графику найдем приближение. Возьмем его как (3.0, 1.0). Теперь найдем решение с его помощью:
Создадим функцию m-файлом fun.m и поместим туда следующий код:
Заметьте, что эта функция принимает вектор приближений и возвращает вектор значений функции. То есть, вместо x здесь x(1), а вместо y — x(2). Это необходимо, потому что fsolve работает с векторами, а не с отдельными переменными.
И наконец, допишем функцию fsolve к коду построения графика таким образом:
Таким образом у нас образуется два m-файла. Первый строит график и вызывает функцию fsolve, а второй необходим для расчета самих значений функций. Если вы что-то не поняли, то в конце статьи будут исходники.
И в конце, приведем результаты:
xr (это вектор решений) =
3.3559 1.2069
fr (это значения функций при таких xr, они должны быть близки к 0) =
1.0e-09 *
0.5420 0.6829
ex (параметр сходимости, если он равен 1, то все сошлось) =
1
И, как же без графика с ответом:
Метод простых итераций в Matlab для решения СНАУ
Теперь переходим к методам, которые запрограммируем сами. Первый из них — метод простых итераций. Он заключается в том, что итеративно приближается к решению, конечно же, с заданной точностью. Алгоритм метода достаточно прост:
- Если возможно, строим график.
- Из каждого уравнения выражаем неизвестную переменную след. образом: из 1 уравнения выражаем x1, из второго — x2, и т.д.
- Выбираем начальное приближение X0, например (3.0 1.0)
- Рассчитываем значение x1, x2. xn, которые получили на шаге 2, подставив значения из приближения X0.
- Проверяем условие сходимости, (X-X0) должно быть меньше точности
- Если 5 пункт не выполнился, то повторяем 4 пункт.
И перейдем к практике, тут станет все понятнее.
Решить систему нелинейных уравнений методом простых итераций с точность 10 -2 :
cos(x-1) + y = 0.5
x-cos(y) = 3
График мы уже строили в предыдущем пункте, поэтому переходим к преобразованию. Увидим, что x из первого уравнения выразить сложно, поэтому поменяем местами уравнения, это не повлияет на решение:
x-cos(y) = 3
cos(x-1) + y = 0.5
Далее приведем код в Matlab:
В этой части мы выразили x1 и x2 (у нас это ‘x’ и ‘y’) и задали точность.
В этой части в цикле выполняются пункты 4-6. То есть итеративно меняются значения x и y, пока отличия от предыдущего значения не станет меньше заданной точности.
k = 10
x = 3.3587
y = 1.2088
Как видно, результаты немного отличаются от предыдущего пункта. Это связано с заданной точностью, можете попробовать поменять точность и увидите, что результаты станут такими же, как и при решении стандартным методом Matlab.
Метод Ньютона в Matlab для решения СНАУ
Решение систем нелинейных уравнений в Matlab методом Ньютона является более эффективным, чем использование метода простых итераций. Сразу же представим алгоритм, а затем перейдем к реализации.
- Если возможно, строим график.
- Выбираем начальное приближение X0, например (3.0 1.0)
- Рассчитываем матрицу Якоби w, это матрица частных производных каждого уравнения, считаем ее определитель для X0.
- Находим вектор приращений, который рассчитывается как dx = -w -1 * f(X0)
- Находим вектор решения X = X0 + dx
- Проверяем условие сходимости, (X-X0) должно быть меньше точности
Далее, решим тот же пример, что и в предыдущих пунктах. Его график мы уже строили и начальное приближение останется таким же.
Решить систему нелинейных уравнений методом Ньютона с точность 10 -2 :
cos(x-1) + y = 0.5
x-cos(y) = 3
Перейдем к коду:
Сначала зададим начальное приближение. Затем необходимо просчитать матрицу Якоби, то есть частные производные по всем переменным. Воспользуемся символьным дифференцированием в Matlab, а именно командой diff с использованием символьных переменных.
Далее, сделаем первую итерацию метода, чтобы получить вектор выходных значений X, а потом уже сравнивать его с приближением в цикле.
В этой части кода выполняем первую итерацию, чтобы получить вектор решения и сравнивать его с вектором начального приближения. Отметим, чтобы посчитать значение символьной функции в Matlab, необходимо воспользоваться функцией subs. Эта функция заменяет переменную на числовое значение. Затем функция double рассчитает это числовое значение.
Все действия, которые были выполнены для расчета производных, на самом деле можно было не производить, а сразу же задать производные. Именно так мы и поступим в цикле.
В этой части кода выполняется цикл по расчету решения с заданной точностью. Еще раз отметим, что если в первой итерации до цикла были использованы функции diff, double и subs для вычисления производной в Matlab, то в самом цикле матрица якоби была явно задана этими частными производными. Это сделано, чтобы показать возможности среды Matlab.
За 3 итерации достигнут правильный результат. Также важно сказать, что иногда такие методы могут зацикливаться и не закончить расчеты. Чтобы такого не было, мы прописали проверку на количество итераций и запретили выполнение более 100 итераций.
Заключение
В этой статье мы познакомились с основными понятиями систем нелинейных алгебраических уравнений в Matlab. Рассмотрели несколько вариантов их решения, как стандартными операторами Matlab, так и запрограммированными методами простых итераций и Ньютона.
Видео:Решение нелинейного уравнения методом простых итераций (программа)Скачать

Как решить уравнение в matlab
Видео:1 3 Решение нелинейных уравнений методом простых итерацийСкачать

Решение нелинейных уравнений в Matlab
Доброго времени суток. В этой статье мы разберем решение простых нелинейных уравнений с помощью средств Matlab. Посмотрим в действии как стандартные функции, так и сами запрограммируем три распространенных метода для решения нелинейных уравнений.
Общая информация
Уравнения, которые содержат переменные, находящиеся в степенях, отличающихся от единицы, или имеющие нелинейные математические выражения (корень, экспонента, логарифм, синус, косинус и т.д.), а также имеющие вид f(x) = 0 называются нелинейными. В зависимости от сложности такого уравнения применяют методы для решения нелинейных уравнений.
В этой статье, помимо стандартных функций Matlab, мы рассмотрим следующие методы:
- Метод перебора
- Метод простых итераций
- Метод половинного деления
Рассмотрим коротко их алгоритмы и применим для решения конкретной задачи.
Стандартные функции Matlab
Для решения нелинейных уравнений в Matlab есть функция fzero. Она принимает в качестве аргументов саму функцию, которую решаем, и отрезок, на котором происходит поиск корней нелинейного уравнения.
И сразу же разберем пример:
Решить нелинейное уравнение x = exp(-x), предварительно определив интервалы, на которых существуют решения уравнения.
Итак, для начала следует привести уравнение к нужному виду: x — exp(-x) = 0 , а затем определить интервалы, в которых будем искать решение уравнения. Методов для определения интервалов множество, но так как пример достаточно прост мы воспользуемся графическим методом.
Здесь задали примерные границы по оси x, чтобы можно было построить график и посмотреть как ведет себя функция. Вот график:
Из графика видно, что на отрезке [0;1] есть корень уравнения (там, где y = 0), соответственно в дальнейшем будем использовать этот интервал. Чем точнее выбран интервал, тем быстрее метод придет к решению уравнения, а для сложных уравнений правильный выбор интервала определяет погрешность, с которой будет получен ответ.
С помощью стандартной функции Matlab находим корень нелинейного уравнения и выводим. Теперь для проверки отобразим все это графически:
Как вы видите, все достаточно точно просчиталось. Теперь мы исследуем эту же функцию с помощью других методов и сравним полученные результаты.
Метод перебора Matlab
Самый простой метод, который заключается в том, что сначала задается какое то приближение x (желательно слева от предполагаемого корня) и значение шага h. Затем, пока выполняется условие f(x) * f(x + h) > 0, значение x увеличивается на значение шага x = x + h. Как только условие перестало выполняться — это значит, что решение нелинейного уравнения находится на интервале [x; x + h].
Теперь реализуем метод перебора в Matlab:
Лучше всего создать новый m-файл, в котором и прописать код. После вызова получаем такой вывод:
Функцию объявляем с помощью очень полезной команды inline, в цикле пока выполняется условие отсутствия корней (или их четного количества), прибавляем к x значение шага. Очевидно, что чем точнее начальное приближение, тем меньше итераций необходимо затратить.
Метод простых итераций Matlab
Этот метод заключается в том, что функцию преобразуют к виду: x = g(x). Эти преобразования можно сделать разными способами, в зависимости от вида начальной функции. Помимо этого следует задать интервал, в котором и будет производиться итерационный процесс, а также начальное приближение. Сам процесс строится по схеме xn= g(xn-1). То есть итерационно проходим от предыдущего значения к последующему.
Процесс заканчивается как только выполнится условие: , то есть, как только будет достигнута заданная точность. И сразу же разберем реализацию метода простых итераций в Matlab для примера, который был приведен выше.
Здесь должно быть все понятно, кроме одного: зачем задавать число итераций? Это нужно для того, чтобы программа не зацикливалась и не выполняла ненужные итерации, а также потому что не всегда программа может просчитать решение с нужной точностью — поэтому следует ограничивать число итераций.
А вот и вывод программы:
Очевидно, что метод простых итераций работает гораздо быстрее и получает точное решение.
Метод половинного деления Matlab
Метод достаточно прост: существует отрезок поиска решения [a;b], сначала находят значение функции в точке середины c, где c = (a+b)/2. Затем сравнивают знаки f(a) и f(c). Если знаки разные — то решение находится на отрезке [a;c], если нет — то решение находится на отрезке [c;b]. Таким образом мы сократили область в 2 раза. Такое сокращение происходит и дальше, пока не достигнем заданной точности.
Перейдем к реализации метода в Matlab:
Все самое важное происходит в цикле: последовательно сокращаем область нахождения решения, пока не будет достигнута заданная точность.
Вот что получилось в выводе:
Этот метод хорошо работает, когда правильно определен интервал, на котором находится решение. Тем не менее, метод простых итераций считается наиболее точным и быстрым.
Заключение
Сегодня мы рассмотрели решение нелинейных уравнений в Matlab. Теперь нам известны методы перебора, половинного деления, простых итераций. А также, когда нам не важно реализация метода, то можно использовать стандартную функцию в Matlab.
На этом все — спасибо за внимание. В следующей статье мы разберем решение систем нелинейных уравнений в matlab.
Видео:1 - Решение систем нелинейных уравнений в MatlabСкачать

Модуль-3-210700 / 2Дисциплина ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЕ ППП-210700 / Раздел-05-ППП-MatLab / Учебное пособие / Тема-05-02-MatLab
Для решения систем алгебраических уравнений и одиночных уравнений служит функция solve:
solve(expr1, expr2. exprN, var1, var2. varN)— возвращает значения переменных var1, при которых соблюдаются равенства, заданные выражениями exprI. Если в выражениях не используются знаки равенства, то полагается ехргI = 0;
solve(expr1, expr2, . exprN)—аналогична предшествующей функции, но переменные, по которым ищется решение, определяются функцией findsym.
Пример 4.2-1. Решить несколько нелинейных уравнений.

Пример4.2-2. Отделить корни уравнения 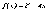
Найдем отрезок, на концах которого 


В математическом пакете MatLab имеется также ряд встроенных функций для численного вычисления корней уравнений.
Рассмотрим программные средства MatLabна примерах.

Решение алгебраических и трансцендентных уравнений в среде MatLAB проще реализовать с помощью встроенных функций: solve(), fzero(), roors().
Для нахождения вещественных корней уравнений вида f(х)=0 используется функция fzero(). Алгоритм, реализованный этой функцией, представляет собой комбинацию метода дихотомии (деления пополам), метода секущих и метода обратной квадратичной интерполяции. В простейшем варианте обращения кроме указателя на функцию, корень которой ищется, задается окрестность х0, с которой начинается поиск: х = fzero(f, x0).
Аргумент fможет быть задан одним из способов:
формойс неизвестным х, заключенная в апострофы;
именем m-файла (в апострофах и без расширения m);
указателем на функцию (например, @f_name);
указателем на анонимную функцию (например, f_handie).
При этом формула, заключенная в апострофы, в качестве независимой переменной может содержать только х. Использование независимой переменной с другим именем вызовет сообщение об ошибке.
Аргумент х0 может быть задан одним из двух способов:
скалярным значением, в окрестности которого предполагается нахождение корня. В этом случае функция fzero() сама пытается найти отрезок с центром в заданной точке х0, на концах которого функцияf ()меняет знак.
Чтобы облегчить работу по выбору начального приближения, разумнее всего построить график функции y=f (x).

Из графика видно, что один из корней находится на интервале [3;4]. Используем полученную информациюи обратимся к функции fzero( ):

Вместо явного задания формулы для функции f мы могли бы объявить соответствующую функцию, запомнив ее в виде автономного m-файла или включив ее в качестве подфункции в файл нашей программы.

Если мы хотим получить не только значение корня, но и узнать значение функции в найденной точке, то к функции fzero( ) можно обратиться с двумя выходными параметрами.
В ряде задач такая точность может оказаться излишней. MatLab предоставляет пользователю возможность формировать различные условия прекращения итерационного процесса — по точности вычисления координаты х, по модулю значения функции f(), по количеству обращений к функции f() и т. д.

Якобы «корень», соответствующий приближенному значению ?/2, на самом деле является точкой разрыва, при переходе через которую функция меняет знак. Выведенное значение функции в найденной точке убеждает нас в том, что найден не корень.
Функция fzero() может возвратить еще два выходных параметра.

Положительное значение e_fiag (обычно, это 1) означает, что удалось найти интервал, на концах которого функция f( ) меняет знак (пример с tg(x)не должен притупить вашу бдительность). Если такой интервал не обнаружен, то e_fiag=-1. Структура inform содержит три поля с именами iterations, funcCountи algorithm. В первом из них находится количество итераций, выполненных при поиске корня, во втором – количество обращений к функции f( ), в третьем – наименование алгоритма, использованного для нахождения корня.
Пример 4.2-6. Найти корень уравнения с помощью функции fzero().

algorithm: ‘bisection, interpolation’
В данном случае достижение высокой точности потребовалось 8 итераций. Простое деление отрезка пополам для достижения такой же точности потребовало бы больше итераций.
Отделение отрезка, на концах которого функция принимает значения разных знаков, является принципиальным для алгоритма, использованного в функции fzero(). Даже в таких тривиальных уравнениях, как х 2 =0, обычно не удается найти решение.
Для символьного (аналитического) решения уравнений в MatLab используется функция solve(),которая представляется в следующем виде:solve(‘f(x)’,x),solve(‘f(x)’),где: ‘f(x)’– решаемое уравнение, записанное в одиночных кавычках и представленное в произвольной форме; x– искомая символьная неизвестная (symsx).
Рассмотрим технологию определения корня с помощью функции solve() на примерах.


Функция в ряде случаев позволяет определить все корни уравнения f(x)=0 без указания начальных значений x или областей изоляции корней.
Функция solve() имеет следующий недостаток. Она не требует информации о начальном значении корня или области его изоляции. Поэтому в случае трансцендентных уравнений и в ряде других случаев, она не находит всех корней уравнения.

Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать

solve
Поддержка вектора символов или входных параметров строки была удалена. Вместо этого используйте syms объявить переменные и входные параметры замены, такие как solve(‘2*x == 1′,’x’) с solve(2*x == 1,x) .
Синтаксис
Описание
S = solve( eqn , var ) решает уравнение eqn для переменной var . Если вы не задаете var , symvar функция определяет переменную, чтобы решить для. Например, solve(x + 1 == 2, x) решает уравнение x + 1 = 2 для x.
S = solve( eqn , var , Name,Value ) дополнительные опции использования заданы одним или несколькими Name,Value парные аргументы.
Y = solve( eqns , vars ) решает систему уравнений eqns для переменных vars и возвращает структуру, которая содержит решения. Если вы не задаете vars , solve использование symvar найти, что переменные решают для. В этом случае, количество переменных это symvar находки равны количеству уравнений eqns .
Y = solve( eqns , vars , Name,Value ) дополнительные опции использования заданы одним или несколькими Name,Value парные аргументы.
[ y1. yN ] = solve( eqns , vars ) решает систему уравнений eqns для переменных vars . Решения присвоены переменным y1. yN . Если вы не задаете переменные, solve использование symvar найти, что переменные решают для. В этом случае, количество переменных это symvar находки равны количеству выходных аргументов N .
[ y1. yN ] = solve( eqns , vars , Name,Value ) дополнительные опции использования заданы одним или несколькими Name,Value парные аргументы.
[ y1. yN , parameters , conditions ] = solve( eqns , vars ,’ ReturnConditions ‘,true) возвращает дополнительные аргументы parameters и conditions это задает параметры в решении и условиях на решении.
Примеры
Решите квадратное уравнение
Решите квадратное уравнение, не задавая переменную, чтобы решить для. solve выбирает x возвратить решение.
Задайте переменную, чтобы решить для и решить квадратное уравнение для a .
Решите полином и возвратите действительные решения
Решите полином пятой степени. Это имеет пять решений.
Возвратите только действительные решения установкой ‘Real’ опция к true . Единственными действительными решениями этого уравнения является 5 .
Численно решите уравнения
Когда solve не может символически решить уравнение, оно пытается найти числовое решение с помощью vpasolve . vpasolve функция возвращает первое найденное решение.
Попытайтесь решить следующее уравнение. solve возвращает числовое решение, потому что оно не может найти символьное решение.
Постройте левые и правые стороны уравнения. Заметьте, что уравнение также имеет положительное решение.
Найдите другое решение путем прямого вызова числового решателя vpasolve и определение интервала.
Решите многомерные уравнения и присвойте Выходные параметры структуре
При решении для нескольких переменных может быть более удобно сохранить выходные параметры в массиве структур, чем в отдельных переменных. solve функция возвращает структуру, когда вы задаете один выходной аргумент, и существуют несколько выходных параметров.
Решите систему уравнений, чтобы возвратить решения в массиве структур.
Доступ к решениям путем обращения к элементам структуры.
Используя массив структур позволяет вам удобно заменять решениями в другие выражения.
Используйте subs функционируйте, чтобы заменить решениями S в другие выражения.
Если solve возвращает пустой объект, затем никакие решения не существуют.
Решите неравенства
solve функция может решить неравенства и возвратить решения, которые удовлетворяют неравенствам. Решите следующие неравенства.
Установите ‘ReturnConditions’ к true возвратить любые параметры в решении и условиях на решении.
Параметры u и v не существуйте в рабочей области MATLAB®, и должен быть получен доступ с помощью S.parameters .
Проверяйте если значения u = 7/2 и v = 1/2 удовлетворите условию с помощью subs и isAlways .
isAlways возвращает логическую единицу ( true ) указание, что эти значения удовлетворяют условию. Замените этими значениями параметров в S.x и S.y найти решение для x и y .
Решите многомерные уравнения и присвойте Выходные параметры переменным
Решите систему уравнений.
При решении больше чем для одной переменной порядок, в котором вы задаете переменные, задает порядок, в котором решатель возвращает решения. Присвойте решения переменных solv и solu путем определения переменных явным образом. Решатель возвращает массив решений для каждой переменной.
Записи с тем же индексом формируют пару решений.
Используйте параметры и условия совершенствовать решение
Возвратите полное решение уравнения параметрами и условиями решения путем определения ‘ReturnConditions’ как true .
Решите уравнение sin ( x ) = 0 . Обеспечьте две дополнительных выходных переменные для выходных аргументов parameters и conditions .
Решение π k содержит параметр k , где k должно быть целое число. Переменная k не существует в рабочем пространстве MATLAB и должен быть получен доступ с помощью parameters .
В качестве альтернативы определите решение для x путем выбора значения k . Проверяйте, удовлетворяет ли выбранное значение условию на k использование isAlways .
Проверяйте если k = 4 удовлетворяет условию на k .
isAlways возвращает логическую единицу ( true ), подразумевать, что 4 допустимое значение для k . Замена k с 4, чтобы получить решение для x . Используйте vpa получить числовое приближение.
Сократите результат с правилами упрощения
Решите уравнение exp ( log ( x ) log ( 3 x ) ) = 4 .
По умолчанию, solve не применяет упрощения, которые не допустимы для всех значений x . В этом случае решатель не принимает это x положительное вещественное число, таким образом, оно не применяет логарифмическую идентичность log ( 3 x ) = log ( 3 ) + log ( x ) . В результате solve не может решить уравнение символически.
Установите ‘IgnoreAnalyticConstraints’ к true применять правила упрощения, которые могут позволить solve найти решение. Для получения дополнительной информации см. Алгоритмы.
solve применяет упрощения, которые позволяют решателю находить решение. Математические правила применялись, когда выполняющие упрощения не всегда допустимы в целом. В этом примере решатель применяет логарифмические тождества учитывая, что x положительное вещественное число. Поэтому решения, найденные в этом режиме, должны быть проверены.
Проигнорируйте предположения на переменных
sym и syms функции позволяют вам установить предположения для символьных переменных.
Примите что переменная x положительно.
Когда вы решаете уравнение для переменной под предположениями, решатель только возвращает решения, сопоставимые с предположениями. Решите это уравнение для x .
Позвольте решения, которые не удовлетворяют предположениям установкой ‘IgnoreProperties’ к true .
Для дальнейших расчетов очистите предположение, что вы устанавливаете на переменной x путем воссоздания его с помощью syms .
Решите полиномиальные знатные уравнения
Когда вы решаете полиномиальное уравнение, решатель может использовать root возвратить решения. Решите полином третьей степени.
Попытайтесь получить явное решение для таких уравнений путем вызова решателя с ‘MaxDegree’ . Опция задает максимальную степень полиномов, для которых решатель пытается возвратить явные решения. Значением по умолчанию является 2 . Увеличивая это значение, можно получить явные решения для полиномов высшего порядка.
Решите те же уравнения для явных решений путем увеличения значения ‘MaxDegree’ к 3 .
Возвратите одно решение
Решите уравнение sin ( x ) + cos ( 2 x ) = 1 .
Вместо того, чтобы возвратить бесконечное множество периодических решений, решатель выбирает три решения, что он считает самым практическим.
Выберите только одно решение установкой ‘PrincipalValue’ к true .
Входные параметры
eqn — Уравнение, чтобы решить
символьное выражение | символьное уравнение
Уравнение, чтобы решить в виде символьного выражения или символьного уравнения. Оператор отношения == определяет символьные уравнения. Если eqn символьное выражение (без правой стороны), решатель принимает, что правая сторона 0 и решает уравнение eqn == 0 .
var — Переменная, для которой вы решаете уравнение
символьная переменная
Переменная, для которой вы решаете уравнение в виде символьной переменной. По умолчанию, solve использует переменную, определенную symvar .
eqns Система уравнений
символьные выражения | символьные уравнения
Система уравнений в виде символьных выражений или символьных уравнений. Если любые элементы eqns символьные выражения (без правой стороны), solve приравнивает элемент к 0 .
vars — Переменные, для которых вы решаете уравнение или систему уравнений
символьный вектор | символьная матрица
Переменные, для которых вы решаете уравнение или систему уравнений в виде символьного вектора или символьной матрицы. По умолчанию, solve использует переменные, определенные symvar .
Порядок, в котором вы задаете эти переменные, задает порядок, в котором решатель возвращает решения.
Аргументы name-value
Real — Отметьте для возврата только действительных решений
false (значение по умолчанию) | true
Отметьте для возврата только действительных решений в виде разделенной запятой пары, состоящей из ‘Real’ и одно из этих значений.
| false | Возвратите все решения. |
| true | Возвратите только те решения, для которых каждое подвыражение исходного уравнения представляет вещественное число. Эта опция также принимает, что все символьные параметры уравнения представляют вещественные числа. |
ReturnConditions — Отметьте для возврата параметров и условий
false (значение по умолчанию) | true
Отметьте для возврата параметров в решении и условиях, при которых решение верно в виде разделенной запятой пары, состоящей из ‘ReturnConditions’ и одно из этих значений.
| false | Не возвращайте параметрированные решения и условия, при которых решение содержит. solve функционируйте заменяет параметры на соответствующие значения. |
| true | Возвратите параметры в решении и условиях, при которых решение содержит. Для вызова с одной выходной переменной, solve возвращает структуру с полями parameters и conditions . Для нескольких выходных переменных, solve присваивает параметры и условия к последним двум выходным переменным. Это поведение означает, что количество выходных переменных должно быть равно количеству переменных, чтобы решить для плюс два. |
Пример: [v1, v2, params, conditions] = solve(sin(x) +y == 0,y^2 == 3,’ReturnConditions’,true) возвращает параметры в params и условия в conditions .
IgnoreAnalyticConstraints — Правила упрощения применились к выражениям и уравнениям
false (значение по умолчанию) | true
Правила упрощения применились к выражениям и уравнениям в виде разделенной запятой пары, состоящей из ‘IgnoreAnalyticConstraints’ и одно из этих значений.
| false | Используйте строгие правила упрощения. |
| true | Примените чисто алгебраические упрощения в выражениях и уравнениях. Установка IgnoreAnalyticConstraints к true может дать вам простые решения, которые могли привести к результатам, не обычно допустимым. Другими словами, эта опция применяет математические тождества, которые удобны, но результаты не могут содержать для всех возможных значений переменных. В некоторых случаях это также включает solve решить уравнения и системы, которые не могут быть решены в противном случае. |
IgnoreProperties — Отметьте для возврата решений, противоречивых со свойствами переменных
false (значение по умолчанию) | true
Отметьте для возврата решений, противоречивых со свойствами переменных в виде разделенной запятой пары, состоящей из ‘IgnoreProperties’ и одно из этих значений.
| false | Не включайте решения, противоречивые со свойствами переменных. |
| true | Включайте решения, противоречивые со свойствами переменных. |
MaxDegree — Максимальная степень полиномиальных уравнений, для которых решатель использует явные формулы
2 (значение по умолчанию) | положительное целое число, меньшее, чем 5
Максимальная степень полиномиальных уравнений, для которых решатель использует явные формулы в виде положительного целого числа, меньшего, чем 5. Решатель не использует явные формулы, которые вовлекают радикалов при решении полиномиальных уравнений степени, больше, чем заданное значение.
PrincipalValue — Отметьте для возврата одного решения
false (значение по умолчанию) | true
Отметьте для возврата одного решения в виде разделенной запятой пары, состоящей из ‘PrincipalValue’ и одно из этих значений.
| false | Возвратите все решения. |
| true | Возвратите только одно решение. Если уравнение или система уравнений не имеют решения, решатель возвращает пустой символьный объект. |
Выходные аргументы
S — Решения уравнения
символьный массив
Решения уравнения, возвращенного как символьный массив. Размер символьного массива соответствует количеству решений.
Y — Решения системы уравнений
структура
Решения системы уравнений, возвращенной как структура. Количество полей в структуре соответствует количеству независимых переменных в системе. Если ‘ReturnConditions’ установлен в true , solve функция возвращает два дополнительных поля, которые содержат параметры в решении и условия, при которых решение верно.
y1. yN — Решения системы уравнений
символьные переменные
Решения системы уравнений, возвращенной как символьные переменные. Количество выходных переменных или символьных массивов должно быть равно количеству независимых переменных в системе. Если вы явным образом задаете независимые переменные vars , затем решатель использует тот же порядок возвратить решения. Если вы не задаете vars , независимые переменные видов тулбокса в алфавитном порядке, и затем присваивают решения для этих переменных к выходным переменным.
parameters — Параметры в решении
вектор из сгенерированных параметров
Параметры в решении, возвращенном как вектор из сгенерированных параметров. Этот выходной аргумент только возвращен если ReturnConditions true . Если один выходной аргумент обеспечивается, parameters возвращен как поле структуры. Если несколько выходных аргументов обеспечиваются, parameters возвращен как предпоследний выходной аргумент. Сгенерированные параметры не появляются в MATLAB ® рабочая область. К ним нужно получить доступ с помощью parameters .
Пример: [solx, params, conditions] = solve(sin(x) == 0, ‘ReturnConditions’, true) возвращает параметр k в аргументе params .
conditions — Условия, при которых решения допустимы
вектор из символьных выражений
Условия, при которых решения допустимы, возвратились как вектор из символьных выражений. Этот выходной аргумент только возвращен если ReturnConditions true . Если один выходной аргумент обеспечивается, conditions возвращен как поле структуры. Если несколько выходных аргументов обеспечиваются, conditions возвращен как последний выходной аргумент.
Пример: [solx, params, conditions] = solve(sin(x) == 0, ‘ReturnConditions’, true) возвращает условие in(k, ‘integer’) в conditions . Решение в solx допустимо только при этом условии.
Советы
Если solve не может найти решение и ReturnConditions false , solve функционируйте внутренне вызывает числовой решатель vpasolve это пытается найти числовое решение. Для полиномиальных уравнений и систем без символьных параметров, числовой решатель возвращает все решения. Для неполиномиальных уравнений и систем без символьных параметров, числовой решатель возвращает только одно решение (если решение существует).
Если solve не может найти решение и ReturnConditions true , solve возвращает пустое решение с предупреждением. Если никакие решения не существуют, solve возвращает пустое решение без предупреждения.
Если решение содержит параметры и ReturnConditions true , solve возвращает параметры в решении и условиях, при которых решения верны. Если ReturnConditions false , solve функционируйте или выбирает значения параметров и возвращает соответствующие результаты или возвращает параметрированные решения, не выбирая особые значения. В последнем случае, solve также выдает предупреждение, указывающее на значения параметров в возвращенных решениях.
Если параметр не появляется ни в каком условии, это означает, что параметр может взять любое комплексное число.
Выход solve может содержать параметры от исходных уравнений в дополнение к параметрам, введенным solve .
Параметры, введенные solve не появляйтесь в рабочем пространстве MATLAB. К ним нужно получить доступ с помощью выходного аргумента, который содержит их. В качестве альтернативы использовать параметры в использовании рабочего пространства MATLAB syms инициализировать параметр. Например, если параметром является k , используйте syms k .
Имена переменных parameters и conditions не позволены как входные параметры solve .
Чтобы решить дифференциальные уравнения, используйте dsolve функция.
При решении системы уравнений всегда присваивайте результат выходным аргументам. Выходные аргументы позволяют вам получить доступ к значениям решений системы.
MaxDegree только принимает положительные целые числа, меньшие, чем 5 потому что, в целом, нет никаких явных выражений для корней полиномов степеней выше, чем 4.
Выходные переменные y1. yN не задавайте переменные для который solve решает уравнения или системы. Если y1. yN переменные, которые появляются в eqns , затем нет никакой гарантии что solve(eqns) присвоит решения y1. yN использование правильного порядка. Таким образом, когда вы запускаете [b,a] = solve(eqns) , вы можете получить решения для a присвоенный b и наоборот.
Чтобы гарантировать порядок возвращенных решений, задайте переменные vars . Например, вызов [b,a] = solve(eqns,b,a) присваивает решения для a к a и решения для b к b .
Алгоритмы
Когда вы используете IgnoreAnalyticConstraints , решатель применяет эти правила к выражениям с обеих сторон уравнения.
регистрируйте (a) + журнал (b) = журнал (a · b) для всех значений a и b. В частности, следующее равенство допустимо для всех значений a, b и c:
журнал (a b ) = b · регистрируйте (a) для всех значений a и b. В частности, следующее равенство допустимо для всех значений a, b и c:
Если f и g являются стандартными математическими функциями и f (g (x)) = x для всех маленьких положительных чисел, f (g (x)) = , x принят, чтобы быть допустимым для всех комплексных чисел x. В частности:
Решатель может умножить обе стороны уравнения по любому выражению кроме 0 .
🎦 Видео
Метод итерацийСкачать

Алгоритмы С#. Метод простых итерацийСкачать

Метод простой итерации Пример РешенияСкачать

Метод Зейделя Пример РешенияСкачать

Решение нелинейного уравнения методом простых итерацийСкачать

4.2 Решение систем нелинейных уравнений. МетодыСкачать

2.2 Итерационные методы решения СЛАУ (Якоби, Зейделя, релаксации)Скачать

10 Численные методы решения нелинейных уравненийСкачать

МЗЭ 2021 Лекция 11 Метод Ньютона для решения систем нелинейных уравненийСкачать

8 Метод простой итерации Ручной счет Решение системы линейных уравнений СЛАУСкачать

Решение численных методов с помощью MATLAB и LatexСкачать

Компьютерное моделирование - Решение систем нелинейных уравненийСкачать

Решение системы нелинейных уравнений. Урок 139Скачать

Метод половинного деления решение нелинейного уравненияСкачать

4 Метод простой итерации Mathcad Решение системы линейных уравнений СЛАУСкачать