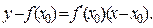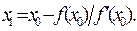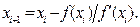| Название | Практическая работа 5 Численное решение нелинейных уравнений в Mathcad (метод простых итераций) |
| Анкор | решение уравнений маткад |
| Дата | 24.02.2021 |
| Размер | 318.5 Kb. |
| Формат файла |  |
| Имя файла | Нелин_уравнения.doc |
| Тип | Практическая работа #179215 |
| Подборка по базе: Итоговая контрольная работа по обществознанию в 10 классе.docx, Практическая работа №3 «Анализ содержания и методического аппара, Контрольная работа.docx, Лабораторная работа 8.doc, Практическая работа №5.docx, Контрольная работа по русскому языку за 1 полугодие.docx, Практическая работа № 5.docx, Практическая работа №5 (1).docx, Практическая работа № 4..docx, Практическая работа №1 Изучение содержаия обновленных ФГОС ООО. Содержание
Видео:Решение нелинейного уравнения методом простых итераций (программа)Скачать  Практическая работа №5Цель работы:
Задание №1.Решить нелинейное уравнение методом итераций. Метод простых итераций является одним из наиболее важных способов численного решения уравнений. Этот метод состоит в следующем. Пусть дано уравнение где f(x) непрерывная функция, требуется определить вещественные корни этого уравнения. Запишем уравнение (1) равносильным уравнением x= Выберем каким-либо способом, например графически, приближенное значение корня x0 и подставим его в правую часть уравнения (2). Получим некоторое число x1= Подставим теперь в правую часть уравнения (3) вместо x0 число x1. Получим новое число x2= Видео:Метод простых итераций пример решения нелинейных уравненийСкачать Задание №1.Решить нелинейное уравнение методом бисекции. Метод бисекции (половинного деления) состоит в следующем. Пусть дано уравнение Деление продолжать до получения отрезка длиной ε ≤ 10-3.
Если Подобная операция необходима для другого конца отрезка [ai, bi], для bi. Если Условный оператор if работает следующим образом. Если логическое выражение, записанное в скобках, истинно, то переменная слева от знака := принимает значение выражения или величины, стоящей первой после логического выражения, в противном случае переменной присваивается значение выражения, или величины, стоящей на втором месте после логического выражения.
Результат на экране: Л Локализация корня уравнения. Д Формулы для определения начала и конца отрезка и определения значения f(x) в середине отрезка. К Методом бисекции (половинного деления) уточнить корень уравнения.
Видео:1 3 Решение нелинейных уравнений методом простых итерацийСкачать  Практическая работа №7Цель работы:
Задание №1.Решить нелинейное уравнение методом Ньютона. Знаменитый метод Ньютона является одним из наиболее эффективных способов численного решения нелинейных уравнений. Этот метод состоит в следующем. Пусть дано уравнение где f(x) непрерывная функция, требуется определить вещественные корни этого уравнения с точностью ε. Расчетная формула метода Ньютона имеет следующий вид Выберем каким-либо способом, например, графически, приближенное значение корня x0 и, подставляя его в правую часть уравнения (2), можем начать итерационный процесс вычисления корня уравнения. Условием завершения итерационного процесса является выполнение условия В случае выполнения неравенства (3), корнем уравнения (1) будем считать значение xk+1. Видео:4 Метод простой итерации Mathcad Решение системы линейных уравнений СЛАУСкачать  Найти действительные корни уравнения с точностью до трех значащих цифр.
x0:a.
Результат на экране: Нелинейное уравнение определено в виде функции. Локализация корней уравнения графическим способом. Приближенное значения корня уравнения. К Н Вычислительная формула Ньютона. Результат вычислений. Расчет погрешности вычислений. Погрешность вычислений становится допустимой на второй итерации Используя метод Ньютона, найти с точностью ε=10-6 положительный корень уравнений Видео:3 Шаговый метод Mathcad Численные методы решения нелинейного уравненияСкачать  Решение нелинейных уравнений в Excel и Mathcad (стр. 1 )
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ Кафедра прикладной математики и вычислительной техники Решение нелинейных уравнений в Excel и Mathcad к выполнению лабораторных работ по дисциплине «Вычислительная математика» Решение нелинейных уравнений в Excel и Mathcad: Метод. указ. / Сост. , — Самара: СГАСУ, 20с. Методические указания разработаны в соответствии с Государственным образовательным стандартом изучения дисциплины «Вычислительная математика». Рассмотрена реализация численных методов при решении нелинейных уравнений и систем уравнений в Excel и MathCad. Приведены варианты заданий для индивидуального выполнения и вопросы для самоконтроля и тестирования. Предназначены для студентов специальности 230201 – «Информационные системы и технологии» всех форм обучения. Рецензент к. ф-м. н. Ó , составление, 2012 1 Решение нелинейного уравнения 1.1 Общие сведения о решении нелинейного уравнения 1.2 Отделение корней 1.3 Уточнение корней стандартными средствами Excel и Mathcad 1.4 Метод деления отрезка пополам 1.6 Метод Ньютона (касательных) 1.7 Комбинированный метод 1.8 Метод итераций 2 Решение систем нелинейных уравнений 2.1 Общие сведения о решении систем нелинейных уравнений 2.2 Решение систем нелинейных уравнений методом Ньютона 2.3 Решение систем нелинейных уравнений методами итераций 3 Задания к лабораторным работам Лабораторная № 1. Отделение корней и стандартные инструменты решения нелинейного уравнения Лабораторная № 2. Сравнение методов уточнения корней нелинейного уравнения Лабораторная № 3. Решение систем нелинейных уравнений Лабораторная № 4. Программирование методов решения нелинейных уравнений и систем 4 Вопросы и тесты для самоконтроля Список рекомендуемой литературы Видео:Метод простой итерации Пример РешенияСкачать  1 Решение нелинейного уравненияВидео:Метод итерацийСкачать  1.1 Общие сведения о решении нелинейного уравненияКак правило, нелинейное уравнения общего вида f(х)=0 невозможно решить аналитически. Для практических задач достаточно найти приближенное значение x, в определенном смысле близкое к точному решению уравнения хточн. В большинстве случаев поиск приближенного решения включает два этапа. На первом этапе отделяют корни, т. е. находят такие отрезки, внутри которых находится строго один корень. На втором этапе уточняют корень на одном из таких отрезков, т. е. находят его значение с требуемой точностью. Достигнутая точность может оцениваться либо «по функции» (в найденной точке x, функция достаточно близка к 0, т. е. выполняется условие |f(x)|≤ ef, где ef требуемая точность по оси ординат), либо «по аргументу» (найден достаточно маленький отрезок [a,b], внутри которого находится корень, т. е. |b–a|≤ ex, где ex требуемая точность по оси абсцисс). Видео:Алгоритмы С#. Метод простых итерацийСкачать  1.2 Отделение корнейОтделение корней может производиться сочетанием графического и аналитического исследования функции. Такое исследование опирается на теорему Вейерштрасса, в соответствии с которой для непрерывной на отрезке [a,b] функции f(х) и любого числа y, отвечающего условию f(a)≤y≤f(b), существует на этом отрезке точка x, в которой функция равна y. Следовательно, для непрерывной функции достаточно найти отрезок, на концах которого функция имеет разные знаки, и можно быть уверенным, что на этом отрезке есть корень уравнения f(х)=0. Для ряда методов уточнения желательно, чтобы найденный на первом этапе отрезок содержал только один корень уравнения. Это условие выполняется, если функция на отрезке монотонна. Монотонность, можно проверить либо по графику функции, либо по знаку производной. Пример Найти с точностью до целых все корни нелинейного уравнения y(x)=x3 ‑ 10x + 7=0 а) построив таблицу и б) построив график. Найти корень уравнения на выделенном отрезке, используя опции «Подбор параметра» и «Поиск решения». Решение Создадим в Excel таблицу, содержащую аргументы и значения функции и по ней построим точечную диаграмму. На рисунке 1 приведен снимок решения. На графике видно, что уравнение имеет три корня, принадлежащие отрезкам [-4, -3], [0, 1] и [2, 3]. Эти отрезки можно выявить и наблюдая за сменой знаков функции в таблице. По построенному графику можно сделать вывод, что на указанных отрезках функция f(x) монотонна и, следовательно, на каждом из них содержится только по одному корню. Такой же анализ может быть выполнен и в пакете Mathcad. Для этого достаточно набрать определение функции f(x), используя оператор присваивания (:=) и естественные общепринятые обозначения математических операций и стандартных функций, задать цикл для изменения аргумента, например, а затем вывести на экран таблицу значений функции (расположенными в одной строке командами x= f(x)=) и график. Цикл можно задать, например, командой x:=-5,-4.5…5. Шаг цикла формируется путем задания начального и следующего за ним значений переменной, а перед конечным значением переменной ставится точка с запятой, которая будет визуально отображена на экране в виде многоточия.
Рисунок 1 – Таблица и график для отделения корней нелинейного уравнения Видео:Решение нелинейного уравнения методом простых итерацийСкачать  1.3 Уточнение корней стандартными средствами Excel и MathcadВо всех методах уточнения корней необходимо задать начальное приближение, которое затем и будет уточняться. Если уравнение имеет несколько корней, в зависимости от выбранного начального приближения будет найден один из них. При неудачно выбранном начальном приближении решение может и не быть найдено. Если в результате первого этапа расчетов уже выделен отрезок, содержащий единственный корень уравнения, в качестве начального приближения можно взять любую точку этого отрезка. В Excel для уточнения значений корней можно использовать опции «Подбор параметра» и «Поиск решения». Пример оформления решения приведен на рисунках 2 и 3.
Рисунок 2 – Ввод значений для использования средств решения уравнения в Excel
Рисунок 3 – Результаты использования средств решения уравнения в Excel В Mathcad для уточнения корней уравнения можно использовать функцию root(….) или блок решения. Пример использования функции root(…) приведен на рисунке 4, а блока решения на рисунке 5. Следует обратить внимание, что в блоке решения (после заголовка блока Given) между левой и правой частями уравнения должен стоять жирный знак равенства (тождества), который можно получить выбором из соответствующей палитры инструментов, либо нажатием одновременно клавиши Ctrl и =.
Рисунок 5 – Решение уравнения с использованием блока решения в Mathcad Как видим, каждый стандартный инструмент находит решение уравнения с определенной точностью. Эта точность зависит от метода, используемого в пакете и, в определенной степени, настроек пакета. Управлять точностью результата здесь достаточно сложно, а часто и невозможно. В то же время, очень просто построить собственную таблицу или написать программу, реализующие один из методов уточнения корней. Здесь можно использовать критерии точности расчета, задаваемые пользователем. При этом достигается и понимание процесса расчетов без опоры на принцип Митрофанушки: «Извозчик есть, довезет». Далее рассмотрены несколько наиболее распространенных методов. Отметим очевидный момент: при прочих равных условиях тот метод уточнения корней будет более эффективен, в котором результат с той же погрешностью найден с меньшим числом вычислений функции f(x) (при этом достигается и максимальная точность при одинаковом числе вычислений функции). Видео:7 Метод половинного деления Mathcad Численные методы решения нелинейного уравненияСкачать  1.4 Метод деления отрезка пополамВ этом методе на каждом шаге отрезок делится на две равные части. Затем сравнивают знаки функции на концах каждой из двух половинок (например, по знаку произведения значений функций на концах), определяют ту из них, в которой содержится решение (знаки функции на концах должны быть разные), и. сужают отрезок, перенося в найденную точку его границу (а или b). Условием окончания служит малость отрезка, где содержится корень («точность по x»), либо близость к 0 значения функции в средине отрезка («точность по y»). Решением уравнения считают середину отрезка, найденного на последнем шаге. Пример. Построить таблицу для уточнения корня уравнения x3 –10x+7=0 на отрезке [-4, -3] методом деления отрезка пополам. Определить сколько шагов надо сделать методом деления отрезка пополам и какая при этом достигается точность по х, для достижения точности по y, равной 0,1; 0,01; 0, 001. Решение Для решения можно использовать табличный процессор Excel, позволяющий автоматически продолжать строки. На первом шаге заносим в таблицу значения левого и правого концов выбранного начального отрезка и вычисляем значение середины отрезка с=(a+b)/2, а затем вводим формулу для вычисления функции в точке a (f(a)) и растягиваем (копируем) её для вычисления f(c) и f(b). В последнем столбца вычисляем выражение (b—a)/2, характеризующего степень точности вычислений. Все набранные формулы можно скопировать во вторую строку таблицы. На втором шаге нужно автоматизировать процесс поиска той половины отрезка, где содержится корень. Для этого испльзуется логическая функция ЕСЛИ (Меню: Вставка Вторую строку таблицы можно продолжить (скопировать) на необходимое число последующих строк. Итерационный процесс завершается, когда очередное значение в последнем столбце становится меньшим, чем заданный показатель точности ex. При этом, значение середины отрезка в последнем приближении, принимается в качестве приближенного значения искомого корня нелинейного уравнения. На рисунке 6 приведен снимок решения. Для построения аналогичного процесса в Mathcad можно использовать бланк, подобный приведенному на рисунке 7. Число шагов N может варьироваться до достижения в таблице результатов требуемой точности. При этом таблица будет автоматически удлиняться или укорачиваться. Итак, одним из трех корней нелинейного уравнения x3 – 10x + 7=0, найденным с точностью e=0,0001, является x= — 3,46686. Как мы видим, он действительно принадлежит отрезку [-4; -3].
Рисунок 6 – Уточнение корня методом деления отрезка пополам в Excel
Рисунок 7 – Уточнение корня методом деления отрезка пополам в Mathcad Видео:11 Метод Ньютона (Метод касательных) Mathcad Численные методы решения нелинейного уравненияСкачать  1.5 Метод хордВ этом методе нелинейная функция f(x) на отделенном интервале [а, b] заменяется линейной – уравнением хорды, т. е. прямой соединяющей граничные точки графика на отрезке. Условие применимости метода – монотонность функции на начальном отрезке, обеспечивающая единственность корня на этом отрезке. Расчет по методу хорд аналогичен расчету методом деления отрезка пополам, но теперь на каждом шаге новая точка x внутри отрезка [a,b] рассчитывается по любой из следующих формул:
Видео:Mathcad Prime. Урок 5 - Способы решения уравненийСкачать  1.6 Метод Ньютона (касательных)Идея, на которой основан метод, аналогична той, которая реализована в методе хорд, только на каждом шаге кривая f(x) заменяется касательной к ней, проведенной в предыдущей найденной точке. В качестве начальной точки в зависимости от свойств функции берется или левая граница отрезка, содержащего корень – x0 = а (если f(а) f»(х) > 0), или правая его граница: x0 = b (если f(b) f»(х)>0). Расчет нового приближения на следующем шаге i+1 производится по формуле:
Алгоритм применим для монотонных функций, сохраняющих выпуклость или вогнутость в промежутке между начальным приближением и корнем уравнения (т. е. должен сохраняться знак первой и второй производных функции f(x)). работоспособен при выпуклых и монотонных функциях f(x). В расчетах нет необходимости отслеживать две границы отрезка, поэтому достаточно на каждом шаге вычислять значения x, f(x) и f′(x). При этом легко оценить «точность по y», по значению левой части уравнения на очередном шаге. Для оценки «точности по x» нужно отслеживать разницу приближений на предыдущем и последующих шагах, которая связана с разницей между найденным приближением и точным значением корня. Следует обратить внимание на следующую особенность метода: последовательность x1, x2, x3,… приближается к корню с другой стороны, в отличие от использования метода хорд при прочих равных условиях. Главным достоинством метода касательных является квадратичная скорость сходимости, что во многих случаях может привести к сокращению числа вычислений функции. Уточнить корень уравнения tg (0,55x+0,1) – x2=0 на отрезке [0.6, 0.8] методом касательных до точности 0,001. Точность вычислений можно оценить из соотношения
Видео:10 Численные методы решения нелинейных уравненийСкачать  2 Решение систем нелинейных уравненийВидео:Метод Ньютона (метод касательных) Пример РешенияСкачать  2.1 Общие сведения о решении систем нелинейных уравненийСистему n нелинейных уравнений с n неизвестными x1, x2, . xn записывают в виде:
где F1, F2,…, Fn – функции независимых переменных, среди которых есть нелинейные. Как и в случае систем линейных уравнений, решением системы является такой вектор X*, который при подстановке обращает одновременно все уравнения системы в тождества.
Система уравнений может не иметь решений, иметь единственное решение, конечное или бесконечное количество решений. Вопрос о количестве решений должен решаться для каждой конкретной задачи отдельно. Численные методы решения системы уравнений носят итерационный характер и требуют задания начального приближения X0. Рассмотрим две группы таких методов: метод Ньютона с различными его модификациями и методы итераций (простых итераций и Зейделя). Видео:2.2 Итерационные методы решения СЛАУ (Якоби, Зейделя, релаксации)Скачать  2.2 Решение систем нелинейных уравнений методом НьютонаБудем рассматривать этот метод на примере системы двух нелинейных уравнений с двумя неизвестными:
Начальные значения x0 и y0 определяются графически. Для нахождения каждого последующего приближения (xi+1, yi+1) используют вектор значений функций и матрицу значений их первых производных, рассчитанные в предыдущей точке (xi, yi).
Для расчета новых приближений на шаге i+1 используется матричная формула
Следует обратить внимание, что в последней формуле используется вычисление матрицы, обратной к матрице первых производных. Расчет останавливают при выполнении одного (а иногда и обоих) из двух условий. Первое из них заключается в том, что на очередном шаге максимальное по модулю из изменений аргументов x и y становится меньше заданная погрешность по аргументам. В соответствии со вторым из условий, на очередном шаге максимальное по модулю значение левых частей уравнений должно отличаться от нуля меньше, чем заданная погрешность по функциям. В упрощенном методе Ньютона матрица производных и матрица, обратная к ней вычисляются только один раз (в начальной точке) и для расчетов используется матричная формула
Приведенные формулы особенно легко записать в Mathcad, где имеются операторы для вычисления производных и действий с матрицами. Однако при правильном использовании матричных операций эти формулы достаточно просто записываются и в Excel. Правда, здесь придется заранее получить формулы для вычисления производных. Для аналитического вычисления производных также может быть использован Mathcad. Видео:Mathcad-09. Пример: уравненияСкачать  2.3 Решение систем нелинейных уравнений методами итерацийДля реализации этих методов исходную систему уравнений необходимо путем алгебраических преобразований явно выразить каждую переменную через остальные. Для случая двух уравнений с двумя неизвестными новая система будет иметь вид
Для решения такой системы задаются начальным приближением x0, y0. Уточненные решения получают по шагам, подставляя в правые части уравнений значения, найденные на предыдущем шаге. В методе простых итераций для уточнения решения используют формулы:
Если одно из решений системы и начальные значения x0 и y0 лежат в области D, задаваемой неравенствами: a ≤ x ≤ b, c ≤ y ≤ d, то расчет по методу простых итераций сходится при выполнении в области D соотношений: Видео:3.Системы нелинейных уравнений MathcadСкачать  Решение нелинейных уравненийДата добавления: 2015-07-23 ; просмотров: 4914 ; Нарушение авторских прав Ознакомиться с основными методами решения нелинейных уравнений и их реализацией в пакете MathCAD. Инженеру часто приходится составлять и решать нелинейные уравнения, что может представлять собой самостоятельную задачу или являться частью более сложных задач. В обоих случаях практическая ценность метода решения определяется быстротой и эффективностью полученного решения, а выбор подходящего метода зависит от характера рассматриваемой задачи. Важно отметить, что к результатам компьютерных вычислений всегда нужно относиться критически, анализировать их на правдоподобность. Чтобы избежать «подводных камней» при использовании любого стандартного пакета, реализующего численные методы, нужно иметь хотя бы минимальное представление о том, какой именно численный метод реализован для решения той или иной задачи. Нелинейные уравнения можно разделить на 2 класса – алгебраические и трансцендентные. Алгебраическими уравнениями называют уравнения, содержащие только алгебраические функции (целые – в частности многочлен, рациональные, иррациональные). Уравнения, содержащие другие функции (тригонометрические, показательные, логарифмические и др.) называются трансцендентными. Нелинейные уравнения могут решаться точными или приближенными методами. Точные методы позволяют записать корни в виде некоторого конечного соотношения (формулы). К сожалению, большинство трансцендентных уравнений, а также произвольные алгебраические уравнения степени выше четвертой не имеют аналитических решений. Кроме того, коэффициенты уравнения могут быть известны лишь приблизительно и, следовательно, сама задача о точном определении корней теряет смысл. Поэтому для решения используются итерационные методы последовательного приближения. Вначале следует вначале отделить корни (т.е. найти их приближенное значение или отрезок их содержащий), а затем методом последовательных приближений их уточнить. Отделить корни можно – установив знаки функции f(x) и ее производной в граничных точках области ее существования, оценив приближенные значения из физического смысла задачи, или из решения аналогичной задачи при других исходных данных. Широко распространен графический способ определения приближенных значений действительных корней – строят график функции f(x) и отмечают точки пересечения его с осью ОХ. Построение графиков часто удается упростить, заменив уравнение f(x)=0 равносильным ему уравнением Пример 1.Графически отделить корни уравнения x lg x = 1. Перепишем его в виде равенства lg x=1/xи найдем абсциссы точек пересечения логарифмической кривой y = lg x и гиперболы y = 1/x (рис. 5). Видно, что единственный корень уравнения
Реализация классических приближенных методов решения в пакете MathCAD. Метод половинного деления Отрезок, на концах которого функция принимает значения разного знака, делится пополам и, если корень лежит правее центральной точки, то к центру подтягивается левый край, а если – левее, то правый край. Новый суженный отрезок снова делится пополам и процедура повторяется. Этот метод прост и надежен, всегда сходится (хотя часто медленно – расплата за простоту!). Программная реализация его в пакете MathCAD рассмотрена в лабораторной работе №7 данного пособия. Метод хорд В качестве последовательных приближений к корню уравнения принимаются значения х1, х2, . хn точек пересечения хорды АВ с осью абсцисс (рис. 6). Уравнение хорды AB имеет вид: Пусть для определенности кривая у = f(x) будет выпукла вниз и, следовательно, расположена ниже своей хорды АВ, т.е. на отрезке [a,b] f ²(x)>0. Возможны два случая: f(а)>0 (рис. 6, а) и f(а) 3 –0,2x 2 –0,2х–1,2 = 0 с точностью e= 0,01. (Точный корень уравнения x = 1,2). Для организации итерационных вычислений в MathCAD документе используется функция until(a, z),котораявозвращает значение величины z, пока выражение a не становится отрицательным.
Метод Ньютона Отличие этого метода от предыдущего состоит в том, что вместо хорды на каждом шаге проводится касательная к кривой y=f(x)при x=хi и ищется точка пересечения ее с осью абсцисс (рис. 7):
При этом не обязательно задавать отрезок [а, b], содержащий корень уравнения), а достаточно лишь задать начальное приближение корня x=х0, которое должно находиться на том же конце интервала [а, b], где знаки функции и ее второй производной совпадают. Уравнение касательной, проведенной к кривой y = f(x) через точку В0 с координатами х0 и f(х0), имеет вид: Отсюда найдем следующее приближение корня х1как абсциссу точки пересечения касательной с осью Ох (y = 0): Аналогично могут быть найдены и последующие приближения как точки пересечения с осью абсцисс касательных, проведенных в точках В1, В2 и так далее. Формула для (i +1) приближения имеет вид:
Условием окончания итерационного процесса является неравенство ïf(xi)ï 1), то процесс итерации может быть расходящимся (рис. 8, в). Пример 4. Решитьуравнение x 3 – x – 1 = 0 методом простой итерации с точностью e = 10 -3 . Реализация этой задачи представлена следующим MathCAD документом.
Реализация приближенных методов решения встроенными функциями MathCAD Использование функции root Для уравнений вида f(x) = 0 решение находится с помощью функции: root(f(х),х,a,b), которая возвращает значение х, принадлежащее отрезку [a, b], при котором выражение или функция f(х)обращается в 0. Оба аргумента этой функции x и f(x) должны быть скалярами, а аргументы a, b– являютсянеобязательными и, если используются, то должны быть вещественными числами, причем a 📸 Видео1.1 Решение нелинейных уравнений метод деления отрезка пополам (бисекций) Мathcad15Скачать  8 Метод простой итерации Ручной счет Решение системы линейных уравнений СЛАУСкачать  Средство для решения систем уравнений в MathCAD 14 (29/34)Скачать  |
(x) (2)
, которое и будет корнем уравнения (2). Итерационный процесс xn= 
. Критерием окончания итерационного процесса является выполнение неравенства
, где ε 3-x-1=0
.
(знаки функции на концах разделенного отрезка разные), то начало нового отрезка для вычислений ai+1 совпадет с ai, т.е. ai+1=ai. В противном случае (знаки функции на концах разделенного отрезка одинаковые) ai+1 совпадет с точкой половинного деления отрезка, т.е. 
.
, то конец нового отрезка для вычислений bi+1 совпадет с точкой половинного деления отрезка, т.е. 
; в противном случае bi+1 совпадет с концом отрезка [ai, bi], т.е. bi+1=bi. Если же 
, то точка 
будет являться корнем нелинейного уравнения. Для реализации описанного процесса в Mathcad запишем формулы для определения начала и конца разделенного отрезка, воспользовавшись условным оператором if в векторной форме. Такая форма записи позволяет в вычислениях Mathcad использовать результаты предыдущих операций. Введем оператор вектора на три элемента и заполним его идентификаторами искомых величин ai+1, bi+1, gi (gi для вычисления 
). Введем знак присвоения и еще один оператор вектора на три элемента. Последний оператор заполните следующими формулами:
. Проанализируем значения вектора ε. Найдем элемент вектора, значение которого меньше заданной в условии задачи минимальной длины отрезка [ai,bi]. В нашем примере это значение элемента ε10. Корнем уравнения будет значение 
.
евая часть нелинейного уравнения, определенная как функция f(x).
искретная переменная i.
Значения длины вычисляемых отрезков.
Длина отрезка [a10, b10] -3 .
начение f(x) наиболее близкое к нулю.
орень уравнения, который можно принять для десяти этапов деления отрезка.
с точностью до 0.0001.
(2)
(3)
. Этим значением будет значение x=a в точке пересечения графика функции с осью абсцисс.
. Результат вычислений погрешности выведите на экран. Корнем уравнения будет x2=1.171.
оличество итераций.
ачальное значение неизвестного для решения уравнения.
, поэтому допустимое решение получено на второй итерации 
.
Рисунок 4 – Решение уравнения с использованием функции root(…) в Mathcad
Функция
.
.
,
.
.
.
.
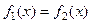, где функции f1(x) и f2(x) — более простые, чем функция f(x). В этом случае следует искать точку пересечения этих графиков.
.
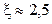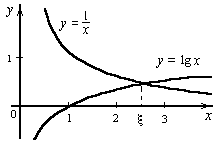Рис. 5. Метод графического отделения корней
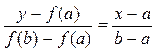. Для точки пересечения ее с осью абсцисс (х=х1, y=0) имеем:
.
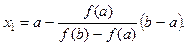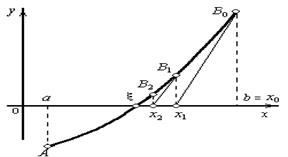Рис. 7. Метод касательных Ньютона
