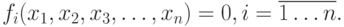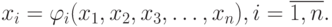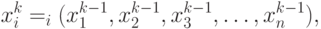Метод простой итерации система нелинейных уравнений примеры

Nickolay.info. Обучение. Лекции по численным методам. Приближённое решение нелинейных алгебраических уравнений

1. Приближенное решение нелинейных алгебраических уравнений

Дано нелинейное алгебраическое уравнение

Видео:Метод простой итерации Пример РешенияСкачать

Нелинейность уравнения означает, что график функции не есть прямая линия, т.е. в f(x) входит x в некоторой степени или под знаком функции.

Решить уравнение – это найти такое x* ∈ R: f(x*)=0. Значение x* называют корнем уравнения. Нелинейное уравнение может иметь несколько корней. Геометрическая интерпретация корней уравнения представлена на рис. 1. Корнями уравнения (1) являются точки x₁*, x₂*, x₃*, в которых функция f(x) пересекает ось x.

Методы решения нелинейного уравнения (1) можно разделить на точные (аналитические) и приближенные (итерационные). В точных методах корень представляется некоторой алгебраической формулой. Например, решение квадратных уравнений, некоторых тригонометрических уравнений и т. д.

В приближенных методах процесс нахождения решения, вообще говоря, бесконечен. Решение получается в виде бесконечной последовательности <x_n>, такой, что . По определению предела, для любого (сколь угодно малого) ε, найдется такое N, что при n>N, |x_n – x*| / (x) не меняет знак на отрезке [a, b], т.е. f(x) – монотонная функция, в этом случае отрезок [a,b] будет интервалом изоляции.

Если корней несколько, то для каждого нужно найти интервал изоляции.

Существуют различные способы исследования функции: аналитический, табличный, графический.

Аналитический способ состоит в нахождении экстремумов функции f(x), исследование ее поведения при и нахождение участков возрастания и убывания функции.

Видео:Метод простых итераций пример решения нелинейных уравненийСкачать

Графический способ – это построение графика функции f(x) и определение числа корней по количеству пересечений графика с осью x.

Табличный способ – это построение таблицы, состоящей из столбца аргумента x и столбца значений функции f(x). О наличии корней свидетельствуют перемены знака функции. Чтобы не произошла потеря корней, шаг изменения аргумента должен быть достаточно мелким, а интервал изменения достаточно широким.

Решить уравнение x 3 ‑ 6x 2 +3x+11=0, т.е. f(x)= x 3 ‑ 6x 2 +3x+11.

Найдем производную f / (x)=3x 2 -12x+3.

Видео:1 3 Решение нелинейных уравнений методом простых итерацийСкачать

Найдем нули производной f / (x)=3x 2 -12x+3=0; D=144-4*3*3=108;

X₁== 0.268;

X₂== 3.732;

Так как f / ()>0, то f / (x)>0 при , f / (x) / (x)>0 при . Кроме того, f()= 0. Следовательно, на интервале возрастает от до f(x₁)= 3x₁ 2 -12x₁+3=11.39; на интервале — убывает до f(x₂)= 3x₂ 2 -12x₂+3=-9.39 и на интервале возрастает до , т.е. уравнение имеет три корня.

Найдем интервалы изоляции для каждого из корней.

Рассмотрим для первого корня отрезок [-2, -1]:

f(-2)= -27 0, f / (x)>0 при т.е. этот отрезок является интервалом изоляции корня.

Рассмотрим для второго корня отрезок [1, 3]:

f(1)= 9>0, f(3)= -7 / (x) 0, f / (x)>0 при т.е. этот отрезок является интервалом изоляции корня.

Моделирование многомерных нелинейных систем.

Видео:Решение нелинейного уравнения методом простых итераций (программа)Скачать

В задачах проектирования и исследования поведения реальных объектов, процессов и систем (ОПС) математические модели должны отображать реальные физические нелинейные процессы. При этом эти процессы зависят, как правило, от многих переменных.

В результате математические модели реальных ОПС описываются системами нелинейных уравнений .

Решение систем нелинейных уравнений

Дана система нелинейных уравнений

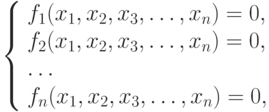( 10.1)

Необходимо решить эту систему, т.е. найти вектор 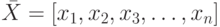, удовлетворяющий системе (10.1) с точностью .

Вектор определяет точку в n-мерном Евклидовом пространстве , т.е. этому пространству и удовлетворяет всем уравнениям системы (10.1).

В отличие от систем линейных уравнений для систем нелинейных уравнений неизвестны прямые методы решения. При решении систем нелинейных уравнений используются итерационные методы. Эффективность всех итерационных методов зависит от выбора начального приближения (начальной точки), т.е. вектора .

Область, в которой начальное приближение сходится к искомому решению, называется областью сходимости G . Если начальное приближение лежит за пределами G , то решение системы получить не удается.

Выбор начальной точки во многом определяется интуицией и опытом специалиста.

Метод простых итераций

Для применения этого метода исходная система (10.1) должна быть преобразована к виду

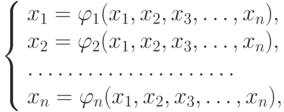( 10.2)

Далее, выбрав начальное приближение и используя систему (10.2), строим итерационный процесс поиска по схеме:

т.е. на каждом k-ом шаге поиска вектор переменных находим, используя значения переменных, полученных на шаге (k-1) .

Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать

Итерационный процесс поиска прекращается как только выполнится условие

( 10.3)

При этом условие (10.3) должно выполняться одновременно по всем переменным.

Метод простых итераций используется для решения таких систем линейных уравнений, в которых выполняется условие сходимости итерационного процесса поиска, а именно:

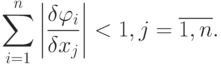( 10.4)

т.е. сумма абсолютных величин частных производных всех преобразованных уравнений системы (10.2) по j-ой переменной меньше единицы.

На рисунке 10.1 представлена схема алгоритма решения систем нелинейных уравнений методом простых итераций .

🔍 Видео

Решение слау методом итераций. Метод простых итераций c++.Скачать

Решение систем линейных уравнений методом простой итерации в ExcelСкачать

8 Метод простой итерации Ручной счет Решение системы линейных уравнений СЛАУСкачать

2.2 Итерационные методы решения СЛАУ (Якоби, Зейделя, релаксации)Скачать

Решение систем линейных уравнений, урок 5/5. Итерационные методыСкачать

10 Численные методы решения нелинейных уравненийСкачать

Метод итерацийСкачать

4.2 Решение систем нелинейных уравнений. МетодыСкачать

Алгоритмы С#. Метод простых итерацийСкачать

4 Метод простой итерации Mathcad Решение системы линейных уравнений СЛАУСкачать

Метод Зейделя Пример РешенияСкачать

Способы решения систем нелинейных уравнений. Практическая часть. 9 класс.Скачать

Решение системы линейных уравнений методом простых итераций в MS ExcelСкачать

Решение системы линейных алгебраических уравнений (СЛАУ) в Excel МАТРИЧНЫМ МЕТОДОМСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать