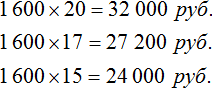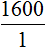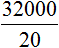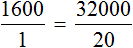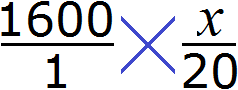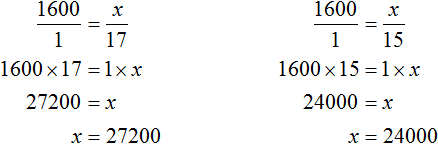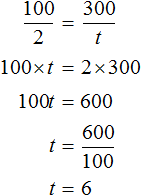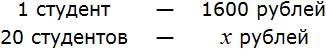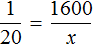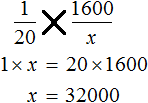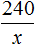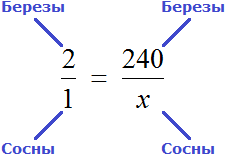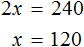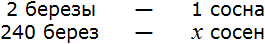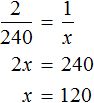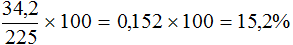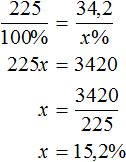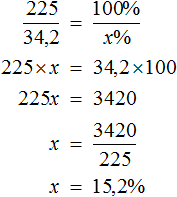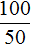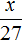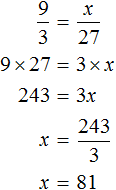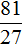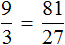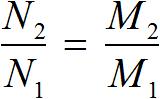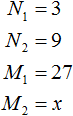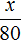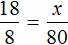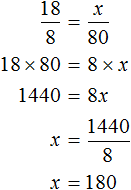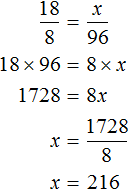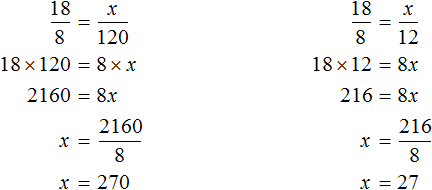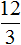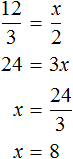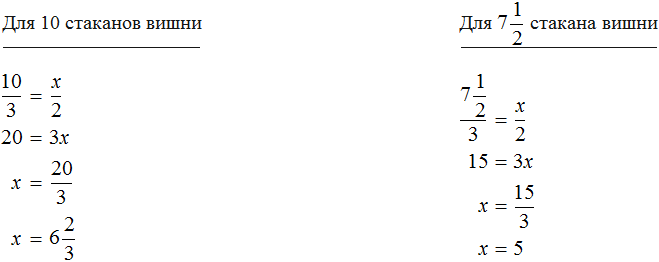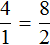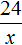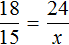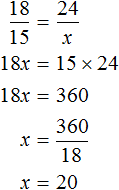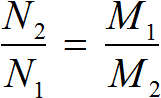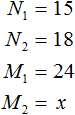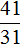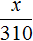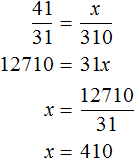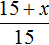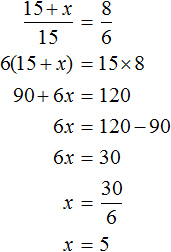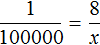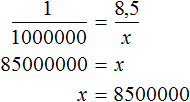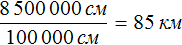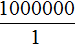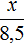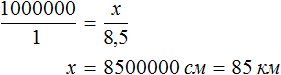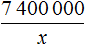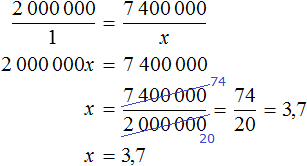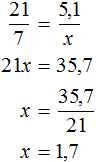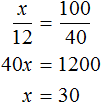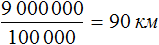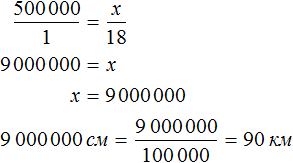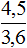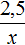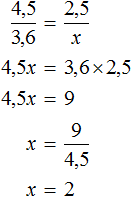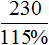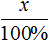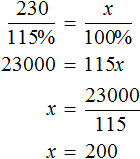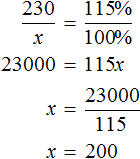Решение задачи с помощью пропорции сводится к тому, чтобы сделать неизвестное значение x членом этой пропорции. Затем используя основное свойство пропорции получить линейное уравнение и решить его.
- Как решить задачу с помощью пропорции
- Отношение одноименных величин
- Задачи на прямую пропорциональность
- Задачи на обратную пропорциональность
- Масштаб
- Задачи для самостоятельного решения
- 11 thoughts on “Решение задач с помощью пропорции”
- Урок 22 Бесплатно Пропорции
- Пропорция
- Как решать пропорции — правила, методы и примеры вычислений
- Общие сведения
- Сферы применения
- Основные свойства
- Методика исследования
- Универсальный алгоритм
- Уравнения с пропорцией
- 💡 Видео
Видео:КАК РЕШАТЬ ПРОПОРЦИИ?Скачать
Как решить задачу с помощью пропорции
Рассмотрим простейший пример. Трем группам нужно выплатить стипендию по 1600 рублей каждому. В первой группе 20 студентов. Значит первой группе будет выплачено 1600 × 20, то есть 32 тыс. рублей.
Во второй группе 17 человек. Значит второй группе будет выплачено 1600 × 17, то есть 27,200 тыс. руб.
Ну и выплатим стипендию третьей группе. В ней 15 человек. На них нужно затратить 1600 × 15, то есть 24 тыс. руб.
В результате имеем следующее решение:
Для подобных задач решение можно записывать с помощью пропорции.
Пропорция по определению есть равенство двух отношений. К примеру, равенство 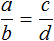
a так относится к b, как c относится d
Аналогично можно соотнести стипендию и студентов, так чтобы каждому досталось по 1600 рублей.
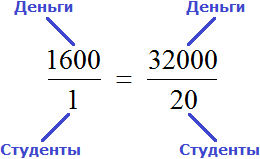
Итак, запишем первое отношение, а именно отношение тысячи шестисот рублей на одного человека:
Мы выяснили, что для выплаты 20 студентам по 1600 рублей, нам потребуется 32 тыс. рублей. Значит второе отношение будет отношением тридцати двух тысяч к двадцати студентам:
Теперь соединим полученные отношения знаком равенства:
Мы получили пропорцию. Её можно прочесть следующим образом:
Тысяча шестьсот рублей так относятся к одному студенту, как тридцать две тысячи рублей относятся к двадцати студентам.
То есть по 1600 рублей каждому. Если выполнить деление в обеих частях равенства 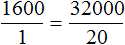
Теперь представим, что сумма денег, необходимых для выплаты стипендии двадцати студентам, была бы неизвестной. Скажем, если бы вопрос стоял так: в группе 20 студентов и каждому нужно выплатить по 1600 рублей. Сколько всего рублей требуется для выплаты стипендии?
В таком случае пропорция 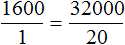
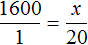
Тысяча шестьсот рублей так относятся к одному студенту, как неизвестное число рублей относится к двадцати студентам
Теперь воспользуемся основным свойством пропорции. Оно гласит, что произведение крайних членов пропорции равно произведению средних:
Перемножив члены пропорции «крест-накрест», получим равенство 1600 × 20 = 1 × x . Вычислив обе части равенства, получим 32000 = x или x = 32000 . Иными словами, мы найдём значение неизвестной величины, которое искали.
Аналогично можно было определить общую сумму и для остального количества студентов — для 17 и 15. Эти пропорции выглядели как 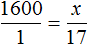
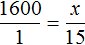
Задача 2. Расстояние равное 100 км автобус проехал за 2 часа. Сколько времени потребуется автобусу, чтобы проехать 300 км, если будет ехать с той же скоростью?
Можно сначала определить расстояние, которое автобус проезжает за один час. Затем определить сколько раз это расстояние содержится в 300 километрах:
100 : 2 = 50 км на каждый час движения
300 км : 50 = 6 часов
Либо можно составить пропорцию «сто километров так относятся к двум часам, как триста километров к неизвестному числу часов»:
Видео:Пропорция. Основное свойство пропорции. Практическая часть - решение задачи. 2 часть. 6 класс.Скачать

Отношение одноименных величин
Если крайние или средние члены пропорции поменять местами, то пропорция не нарушится.
Так, в пропорции 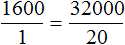
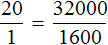
Пропорция также не нарушится, если её перевернуть, то есть использовать обратные отношения в обеих частях.
Перевернем пропорцию 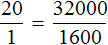
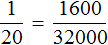
Этот способ записи очень удобен, поскольку позволяет перевести условие задачи в более понятный вид. Решим задачу в которой требовалось определить сколько рублей нужно для выплаты стипендии двадцати студентам.
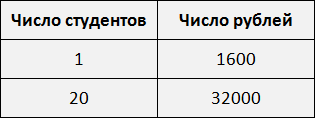
Условие задачи запишем следующим образом:
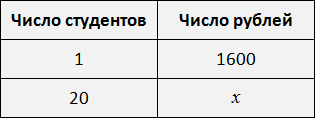
Составим таблицу на основе этого условия:
Составим пропорцию, используя данные таблицы:
Используя основное свойство пропорции, получим линейное уравнение и найдем его корень:
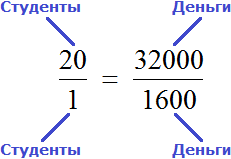
Изначально, мы имели дело с пропорцией 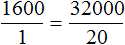
Поменяв местами крайние члены, мы получили пропорцию 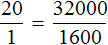
Если отношение составлено из величин одной природы, то мы будем называть его отношением одноименных величин. Например, отношения между фруктами, деньгами, физическими величинами, явлениями, действиями.
Отношение может быть составлено, как из одноименных величин, так и из величин разной природы. Примерами последних являются отношение расстояния ко времени, отношения стоимости товара к его количеству, отношение общей суммы стипендии к количеству студентов.
Пример 2. В школьном саду посажены сосны и березы, причём на каждую сосну приходится 2 березы. Сколько посадили сосен в саду, если берез посадили 240?
Определим сколько сосен было посажено в саду. Для этого составим пропорцию. В условии сказано, что на каждую сосну приходится 2 березы. Напишем отношение, показывающее что на одну сосну приходится две березы:
Теперь напишем второе отношение, показывающее что на x сосен приходится 240 берез
Соединим эти отношения знаком равенства, получим следующую пропорцию:
«2 березы так относятся к одной сосне,
как 240 берез относятся к x соснам»
Используя основное свойство пропорции, находим значение x
Либо пропорцию можно составить, предварительно записав условие, как в прошлом примере:
Получится та же пропорция, но в этот раз она будет составлена из отношений одноименных величин:
Значит в саду посадили 120 сосен.
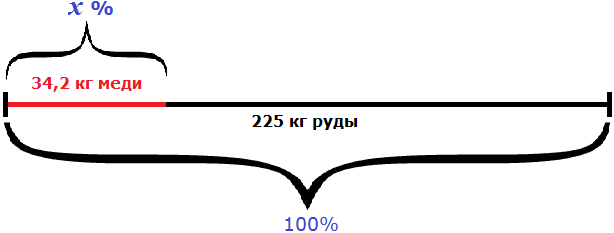
Пример 3. Из 225 кг руды получили 34,2 кг меди. Каково процентное содержание меди в руде?
Можно разделить 34,2 на 225 и полученный результат выразить в процентах:
Либо составить пропорцию 225 килограммам руды так приходятся на 100%, как 34,2 кг меди приходятся на неизвестное число процентов:
Либо составить пропорцию в которой отношения составлены из одноименных величин:
Видео:Пропорция. Основное свойство пропорции. 6 класс.Скачать
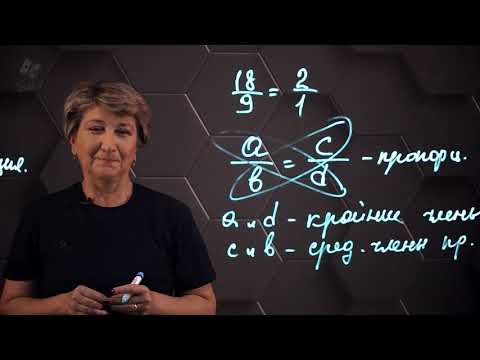
Задачи на прямую пропорциональность
Понимание отношений одноименных величин приводит к пониманию решения задач на прямую и обратную пропорциональность. Начнем с задач на прямую пропорциональность.
Для начала вспомним, что такое прямая пропорциональность. Это взаимосвязь между двумя величинами при которой увеличение одной из них влечет за собой увеличение другой во столько же раз.
Если расстояние в 50 км автобус прошел за 1 час, то для прохождения расстояния в 100 км (при той же скорости) автобусу потребуется 2 часа. Во сколько раз увеличилось расстояние, во столько же раз увеличилось время движения. Как показать это с помощью пропорции?
Одно из предназначений отношения заключается в том, чтобы показать во сколько раз первая величина больше второй. А значит и мы c помощью пропорции можем показать, что расстояние и время увеличились в два раза. Для этого воспользуемся отношением одноименных величин.
Покажем, что расстояние увеличилось в два раза:
Аналогично покажем, что время увеличилось во столько же раз
Соединим эти отношения знаком равенства, получим пропорцию:
«100 километров так относятся к 50 километрам, как 2 часа относятся к 1 часу»
Если выполнить деление в обеих частях равенства 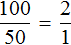
Задача 2. За 3 ч на мельнице смололи 27 т пшеничной муки. Сколько тонн пшеничной муки можно смолоть за 9 ч, если темп работы не изменится?
Решение
Время работы мельницы и масса перемолотой муки — прямо пропорциональные величины. При увеличении времени работы в несколько раз, количество перемолотой муки увеличится во столько же раз. Покажем это с помощью пропорции.
В задаче дано 3 ч. Эти 3 ч увеличились до 9 ч. Запишем отношение 9 ч к 3 ч. Это отношение будет показывать во сколько раз увеличилось время работы мельницы:
Теперь запишем второе отношение. Это будет отношение x тонн пшеничной муки к 27 тоннам. Данное отношение будет показывать, что количество перемолотой муки увеличилось во столько же раз, сколько и время работы мельницы
Соединим эти отношения знаком равенства, получим пропорцию 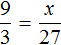
Воспользуемся основным свойством пропорции и найдем x
Значит за 9 ч можно смолоть 81 т пшеничной муки.
Вообще, если взять две прямо пропорциональные величины и увеличить их в одинаковое число раз, то отношение нового значения к старому значению первой величины будет равно отношению нового значения к старому значению второй величины.
Так и в предыдущей задаче старые значения были 3 ч и 27 т. Эти значения были увеличены в одинаковое число раз (в три раза). Новыми значениями стали 9 ч и 81 т. Тогда отношение нового значения времени работы мельницы к старому значению 
Если выполнить деление в обеих частях равенства, то обнаружим, что время работы мельницы и количество смолотой муки увеличилось в одинаковое число раз:
Пропорцию, которую составляют к задачам на прямую пропорциональность, можно описать с помощью выражения:
| Где | 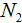 − новое значение первой величины − новое значение первой величины |
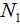 − старое значение первой величины − старое значение первой величины | |
| − новое значение второй величины | |
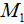 − старое значение второй величины − старое значение второй величины |
Применительно к нашей задаче значения переменных 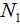
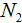
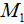
Где впоследствии стало равно 81.
Задача 2. Для 8 коров в зимнее время доярка ежедневно заготовляет 80 кг сена, 96 кг корнеплодов, 120 кг силоса и 12 кг концентратов. Определить ежедневный расход этих кормов для 18 коров.
Решение
Количество коров и масса каждого из кормов — прямо пропорциональные величины. При увеличении количества коров в несколько раз, масса каждого из кормов увеличится во столько же раз.
Составим несколько пропорций, вычисляющих массу каждого из кормов для 18 коров.
Начнем с сена. Ежедневно для 8 коров его заготовляют 80 кг. Тогда для 18 коров будет заготовлено x кг сена.
Запишем отношение, показывающее во сколько раз увеличилось количество коров:
Теперь запишем отношение, показывающее во сколько раз увеличилась масса сена:
Соединим эти отношения знаком равенства, получим пропорцию:
Отсюда находим x
Значит для 18 коров нужно заготовить 180 кг сена. Аналогично определяем массу корнеплодов, силоса и концентратов.
Для 8 коров ежедневно заготовляют 96 кг корнеплодов. Тогда для 18 коров будет заготовлено x кг корнеплодов. Составим пропорцию из отношений 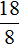
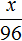
Определим сколько силоса и концентратов нужно заготовить для 18 коров:
Значит для 18 коров ежедневно нужно заготавливать 180 кг сена, 216 кг корнеплодов, 270 кг силоса и 27 кг концентратов.
Задача 3. Хозяйка варит вишнёвое варенье, причём на 3 стакана вишни кладёт 2 стакана сахара. Сколько сахара нужно положить на 12 стаканов вишни? на 10 стаканов вишни? на 
Решение
Количество стаканов вишни и количество стаканов сахарного песка — прямо пропорциональные величины. При увеличении количества стаканов вишни в несколько раз, количество стаканов сахара увеличится во столько же раз.
Запишем отношение, показывающее во сколько раз увеличилось количество стаканов вишни:
Теперь запишем отношение, показывающее во сколько раз увеличилось количество стаканов сахара:
Соединим эти отношения знаком равенства, получим пропорцию и найдем значение x
Значит на 12 стаканов вишни нужно положить 8 стаканов сахара.
Определим количество стаканов сахара для 10 стаканов вишни и 
Видео:Решение уравнений, имеющих вид пропорции, с использованием основного свойства пропорции Математика 6Скачать

Задачи на обратную пропорциональность
Для решения задач на обратную пропорциональность опять же можно использовать пропорцию, составленную из отношений одноименных величин.
В отличие от прямой пропорциональности, где величины увеличиваются или уменьшаются в одну и ту же сторону, в обратной пропорциональности величины изменяются обратно друг другу.
Если одна величина увеличивается в несколько раз, то другая уменьшается во столько же раз. И наоборот, если одна величина уменьшается в несколько раз, то другая увеличивается во столько же раз.
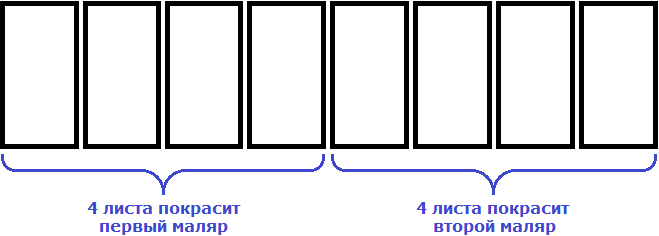
Допустим, что нужно покрасить забор, состоящий из 8 листов
Один маляр будет красить все 8 листов сам
Если маляров будет 2, то каждый покрасит по 4 листа.
Это конечно же при условии, что маляры будут честными между собой и справедливо разделят эту работу поровну на двоих.
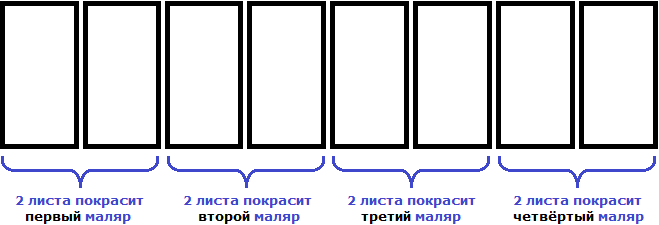
Если маляров будет 4, то каждый покрасит по 2 листа
Замечаем, что при увеличении количества маляров в несколько раз, количество листов которые приходятся на одного маляра уменьшаются во столько же раз.
Итак, мы увеличили количество маляров с 1 до 4. Другими словами, увеличили количество маляров в четыре раза. Запишем это с помощью отношения:
В результате количество листов забора, которые приходятся на одного маляра уменьшилось в четыре раза. Запишем это с помощью отношения:
Соединим эти отношения знаком равенства, получим пропорцию
«4 маляра так относятся к 1 маляру, как 8 листов относятся к 2 листам»
Задача 2. 15 рабочих закончили отделку квартир в новом доме за 24 дня. За сколько дней выполнили бы эту работу 18 рабочих?
Решение
Количество рабочих и количество дней, затраченных на работу — обратно пропорциональные величины. При увеличении количества рабочих в несколько раз, количество дней, необходимых для выполнения этой работы, уменьшится во столько же раз.
Запишем отношение 18 рабочих к 15 рабочим. Это отношение будет показывать во сколько раз увеличилось количество рабочих
Теперь запишем второе отношение, показывающее во сколько раз уменьшилось количество дней. Поскольку количество дней уменьшится с 24 дней до x дней, то второе отношение будет отношением старого количества дней (24 дня) к новому количеству дней (x дней)
Соединим полученные отношения знаком равенства, получим пропорцию:
Отсюда находим x
Значит 18 рабочих выполнят необходимую работу за 20 дней.
Вообще, если взять две обратно пропорциональные величины и увеличить одну из них в определенное число раз, то другая уменьшится во столько же раз. Тогда отношение нового значения к старому значению первой величины будет равно отношению старого значения к новому значению второй величины.
Так и в предыдущей задаче старые значения были 15 рабочих и 24 дня. Количество рабочих было увеличено с 15 до 18 (т.е. было увеличено в 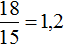
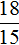
Для составления пропорции к задачам на обратную пропорциональность можно пользоваться формулой:
| Где | 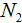 − новое значение первой величины − новое значение первой величины |
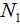 − старое значение первой величины − старое значение первой величины | |
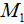 − старое значение второй величины − старое значение второй величины | |
| − новое значение второй величины |
Применительно к нашей задаче значения переменных 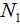
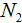
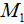
Где впоследствии стало равно 20.
Задача 2. Скорость парохода относится к скорости течения реки, как 36 : 5. Пароход двигался вниз по течению 5 ч 10 мин. Сколько времени потребуется ему, чтобы вернуться обратно?
Решение
Собственная скорость парохода составляет 36 км/ч. Скорость течения реки реки 5 км/ч. Поскольку пароход двигался по течению руки, то скорость его движения составила 36 + 5 = 41 км/ч. Время пути составила 5 ч 10 мин. Для удобства выразим время в минутах:
5 ч 10 мин = 300 мин + 10 мин = 310 мин
Поскольку на обратном пути пароход двигался против течения реки, то его скорость составила 36 − 5 = 31 км/ч.
Скорость парохода и время его движения — обратно пропорциональные величины. При уменьшении скорости в несколько раз, время его движения увеличится во столько же раз.
Запишем отношение, показывающее во сколько раз уменьшилась скорость движения:
Теперь запишем второе отношение, показывающее во сколько раз увеличилось время движения. Поскольку новое время x будет больше старого времени, в числителе отношения запишем время x , а в знаменателе старое время, равное трёхсот десяти минутам
Соединим полученные отношения знаком равенства, получим пропорцию 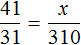
410 минут это 6 часов и 50 минут. Значит пароходу потребуется 6 часов и 50 минут, чтобы вернуться обратно.
Задача 3. На ремонте дороги работало 15 человек, и они должны были закончить работу за 12 дней. На пятый день утром подошли еще несколько рабочих, и оставшаяся работа была выполнена за 6 дней. Сколько рабочих прибыло дополнительно?
Решение
Вычтем из 12 дней 4 отработанных дня. Так мы определим сколько ещё дней осталось работать пятнадцати рабочим
12 дней − 4 дня = 8 дней
На пятый день дополнительно прибыло x рабочих. Тогда всего рабочих стало 15 + x .
Количество рабочих и количество дней, необходимых для выполнения работы — обратно пропорциональные величины. При увеличении количества рабочих в несколько раз, количество дней уменьшится во столько же раз.
Запишем отношение, показывающее во сколько раз увеличилось количество рабочих:
Теперь запишем во сколько раз уменьшилось количество дней, необходимых для выполнения работы:
Соединим эти отношения знаком равенства, получим пропорцию 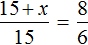
Значит 5 рабочих прибыло дополнительно.
Видео:Пропорция. Основное свойство пропорции. Практическая часть - решение задачи. 1 часть. 6 класс.Скачать

Масштаб
Масштабом называют отношение длины отрезка на изображении к длине соответствующего отрезка на местности.
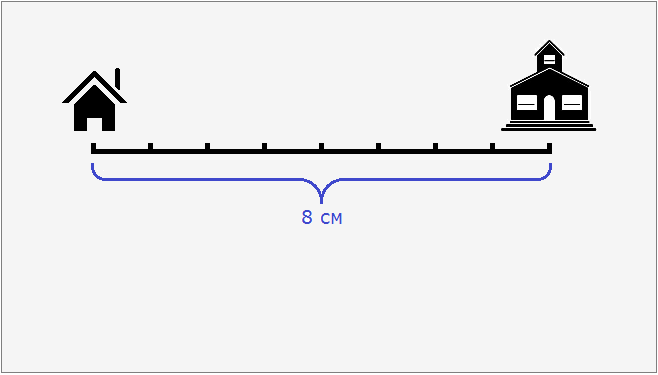
Допустим, что расстояние от дома до школы составляет 8 км. Попробуем нарисовать план местности, где будут указаны дом, школа и расстояние между ними. Но изобразить на бумаге расстояние, равное 8 км мы не можем, поскольку оно довольно велико. Но зато мы можем уменьшить это расстояние в несколько раз так, чтобы оно уместилось на бумаге.
Пусть километры на местности на нашем плане будут выражаться в сантиметрах. Переведем 8 километров в сантиметры, получим 800 000 сантиметров.
Уменьшим 800 000 см в сто тысяч раз:
800 000 см : 100 000 см = 8 см
8 см это расстояние от дома до школы, уменьшенное в сто тысяч раз. Теперь без труда можно нарисовать на бумаге дом и школу, расстояние между которыми будет 8 см.
Эти 8 см относятся к реальным 800 000 см. Так и запишем с помощью отношения:
Одно из свойств отношения гласит, что отношение не меняется если его члены умножить или разделить на одно и то же число.
В целях упрощения отношения 8 : 800 000 оба его члена можно разделить на 8. Тогда получим отношение 1 : 100 000. Это отношение и назовём масштабом. Данное отношение показывает, что один сантиметр на плане относится (или соответствует) ста тысячам сантиметров на местности.
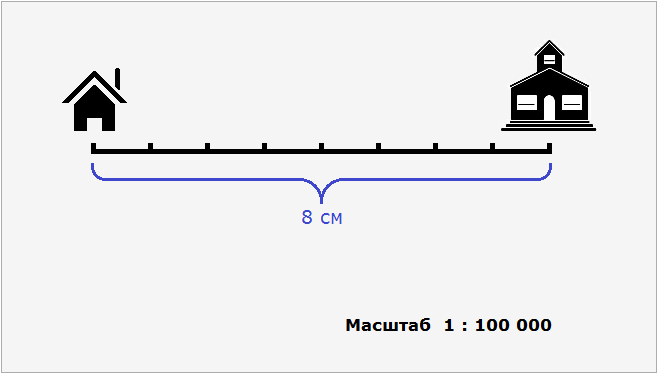
Поэтому на нашем рисунке необходимо указать, что план составлен в масштабе 1 : 100 000
1 см на плане относится к 100 000 см на местности;
2 см на плане относится к 200000 см на местности;
3 см на плане относится к 300000 на местности и т.д.
К любой карте или плану указывается в каком масштабе они сделаны. Этот масштаб позволяет определять реальное расстояние между объектами.
Так, наш план составлен в масштабе 1 : 100 000. На этом плане расстояние между домом и школой составляет 8 см. Чтобы вычислить реальное расстояние между домом и школой, нужно 8 см увеличить в 100 000 раз. Иными словами, умножить 8 см на 100 000
8 см × 100 000 = 800 000 см
Получаем 800 000 см или 8 км, если перевести сантиметры в километры.
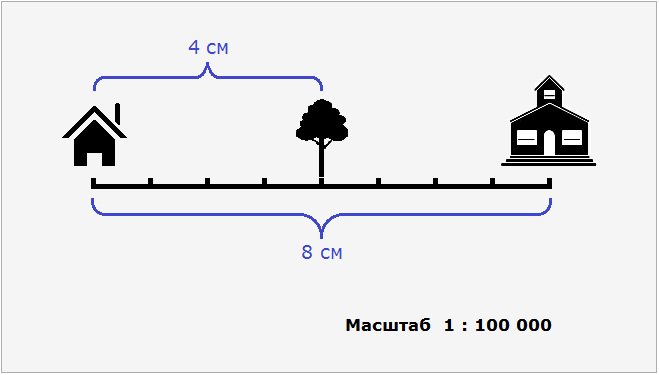
Допустим, что между домом и школой располагается дерево. На плане расстояние между школой и этим деревом составляет 4 см.
Тогда реальное расстояние между домом и деревом будет 4 см × 100 000 = 400 000 см или 4 км.
Расстояние на местности можно определять с помощью пропорции. В нашем примере расстояние между домом и школой будет вычисляться с помощью следующей пропорции:
Эту пропорцию можно прочитать так:
1 см на плане так относится к 100000 см на местности, как 8 см на плане относятся к x см на местности.
Из этой пропорции узнаём, что значение x равно 800000 см.
Пример 2. На карте расстояние между двумя городами составляет 8,5 см. Определить реальное расстояние между городами, если карта составлена в масштабе 1 : 1 000 000.
Решение
Масштаб 1 : 1 000 000 указывает, что 1 см на карте соответствует 1 000 000 см на местности. Тогда 8,5 см будут соответствовать x см на местности. Составим пропорцию 1 к 1000000 как 8,5 к x
В 1 км содержится 100000 см. Тогда в 8 500 000 см будет
Либо можно рассуждать так. Расстояние на карте и расстояние на местности — прямо пропорциональные величины. При увеличении расстояния на карте в несколько раз, расстояние на местности увеличится во столько же раз. Тогда пропорция примет следующий вид. Первое отношение будет показывать во сколько раз расстояние на местности больше расстояния на карте:
Второе отношение покажет, что расстояние на местности во столько же раз больше, чем 8,5 см на карте:
Отсюда x равен 8 500 000 см или 85 км.
Задача 3. Длина реки Невы 74 км. Чему равняется ее длина на карте, масштаб которой 1 : 2 000 000
Решение
Масштаб 1 : 2000000 говорит о том, что 1 см на карте соответствует 2 000 000 см на местности.
А 74 км на это 74 × 100 000 = 7 400 000 см на местности. Уменьшив 7 400 000 в 2 000 000, мы определим длину реки Невы на карте
7 400 000 : 2 000 000 = 3,7 см
Значит на карте, масштаб которой 1 : 2 000 000 длина реки Невы составляет 3,7 см.
Запишем решение с помощью пропорции. Первое отношение будет показывать сколько раз длина на карте меньше длины на местности:
Второе отношение будет показывать, что 74 км (7 400 000 см) уменьшились во столько же раз:
Отсюда находим x равный 3,7 см
Видео:Метод пропорции ⚖️Скачать

Задачи для самостоятельного решения
Решение
Пусть x кг масла можно получить из 7 кг хлопкового семени. Масса хлопкового семени и масса получаемого масла — прямо пропорциональные величины. Тогда уменьшение хлопкового семени с 21 кг до 7 кг, приведет к уменьшению получаемого масла во столько же раз.
Ответ: из 7 кг хлопкового семени получится 1,7 кг масла.
Решение
Длина участка на котором производится замена рельсов равна 8 × 360 = 2880 м.
Пусть x двенадцатиметровых рельсов требуется для замены. Увеличение длины одного рельса с 8 м до 12 м приведет к уменьшению количества рельсов с 360 до x штук. Иными словами, длина рельса и их количество связаны обратно пропорциональной зависимостью
Ответ: для замены старых рельсов потребуется 240 новых.
Решение
Если 60% учащихся пошли в кино, а остальные 12 человек на выставку, то на 40% учащихся и будут приходиться 12 человек, пошедших на выставку. Тогда можно составить пропорцию в которой 12 учащихся так относятся к 40%, как все x учащихся относятся к 100%
Либо можно составить пропорцию, состоящей из отношений одноименных величин. Количество учащихся и процентная доля изменяются прямо пропорционально. Тогда можно записать, что во сколько раз увеличилось количество участников 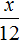
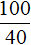
Ответ: в классе 30 учащихся.
Решение
Масштаб 1 : 500000 говорит о том, что 1 см на карте соответствует 500 000 см на местности.
Тогда увеличив 18 см в 500 000, мы получим действительное расстояние между городами
18 см × 500 000 = 9 000 000 см
Переведем 9 000 000 см в километры. В одном километре 100 000 см. Тогда в 9 000 000 см будет
Запишем решение с помощью пропорции:
Ответ: расстояние между городами 90 км.
Решение
Скорость и время — обратно пропорциональные величины. При увеличении скорости в несколько раз, время движения уменьшится во столько же раз.
Запишем отношение, показывающее по сколько раз увеличилась скорость движения пешехода:
Запишем отношение, показывающее что время движения уменьшилось во столько же раз:
Соединим эти отношения знаком равенства, получим пропорцию и найдём значение x
Ответ: пешеход затратит 2 часа если будет двигаться со скорость 4,5 км/ч.
Решение
Выражение «перевыполнили план на 15%» означает, что к имеющемуся 100% плану выполнили еще 15% того же плана. Итого выполнено 115% плана. На эти 115% приходятся 230 выпущенных станков
А по плану завод должен был выпустить x станков. Эти x станков приходятся на 100% изначального плана
Составим пропорцию из имеющихся отношений и найдём значение x
Либо можно воспользоваться отношениями одноименных величин. Количество выпущенных станков и процентная доля, на которые эти станки приходятся, связаны прямо пропорциональной зависимостью. При увеличении количества станков в несколько раз, процентная доля увеличивается во столько же раз. Тогда можно записать, что 230 станков во столько раз больше, чем x станков, во сколько раз больше 115%, чем 100%
Ответ: по плану завод должен был выпустить 200 станков.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Видео:6 класс - Математика - Пропорции. Решение уравнений с помощью пропорцийСкачать

11 thoughts on “Решение задач с помощью пропорции”
Огромное спасибо за урок! Мне мама пыталась объяснить пропорции, а я не понимала) А теперь все просто благодаря вам!
Боже мой, почему мне так сложно? 🙁
Сразу не получится. Нужно время
Отличный урок! Пожалуйста, не забрасывайте этот проект, популяризировать математику необходимо. Уверен, многие люди, как и я, готовы поддержать Вас рублём, если вы дадите такую возможность. Большое спасибо за уже проделанную Вами работу, людей необходимо просвещать, особенно в наше время.
В разделе « решение задач с помощью пропорции» в задаче 2 есть фраза «сто километров так относятся к одному часу, как триста километров к неизвестному числу часов»:» и составлена пропорция 100/2= 300/x. Во
фразе опечатка, 100 километров при составлении пропорции относится к 2 часам а не к одному.
«составленнаю из отношений одноименных величин.» -> составленную
Видео:Решение уравнений методом пропорцииСкачать

Урок 22 Бесплатно Пропорции
Чтобы узнать название темы урока, обратите внимание на картинку.
Попробуйте отгадать ребус.
На этом уроке вы узнаете, что называют пропорцией, выведете основное свойство пропорции и с помощью него научитесь решать задачи и уравнения.
Слово «пропорция» (proportio) в переводе с латинского — соразмерность, отношение частей (соотношение).
Видео:РЕШЕНИЕ УРАВНЕНИЙ ДОМНОЖЕНИЕМ И МЕТОДОМ ПРОПОРЦИИСкачать

Пропорция
В IV веке до н.э. древнегреческий математик Евдокс Книдский дал определение пропорции, состоящей из величин любой природы, а не только из натуральных величин.
Пропорции применяли с древности при решении различных задач.
Древние греки использовали пропорцию и ее свойство для строительства сооружений, при создании произведений искусства (скульптуры, статуи), в ремесленническом деле и др.
Соблюдение пропорций, определенных соотношений, активно используется и в настоящее время в архитектуре, искусстве, музыке, при решении физических задач.
В географии и моделировании пропорциональные зависимости применяют при создании уменьшенной копии реального объекта.
В швейных технологиях — для изменения размеров выкройки изделия до нужного размера.
В химии для проведения успешной реакции рассчитывают пропорциональное отношение химических веществ.
В медицине и фармацевтике используют пропорции при изготовлении лекарственных препаратов.
В кулинарии, например, с помощью пропорции можно рассчитать рецепт одного и того же блюда для разного количества гостей.
Разберем, что же такое пропорция в математическом понимании.
Возьмем два отношения: (mathbf<frac>) и (mathbf<frac>) и эти отношения равны, так как (mathbf) и (mathbf), значит (mathbf<frac= frac>)
Равенство двух отношений называют пропорцией.
С помощью букв запишем пропорцию из двух отношений так: (mathbf) или (mathbf<frac= frac>).
Эту математическую запись читают так: «Отношение a к b равно отношению c к d» или «a так относится к b, как c относится к d».
Все члены пропорции не равны нулю: (mathbf).
Числа a и d называют крайними членами пропорции.
Числа b и c называют средними членами пропорции.
У меня есть дополнительная информация к этой части урока!
В мире существует «золотая пропорция», которую называют «золотым сечением». Это пропорциональное деление отрезка на различные по размеру части, но в таком соотношении к друг другу, что меньший отрезок так относится к большему, как больший ко всей величине.
Приблизительное значение «золотого сечения» равно 1,618… Число это продолжается бесконечно после запятой, и оно не периодично.
В процентном выражении целая часть относится к большей, как большая к меньшей, примерно так: 62% и 38% соответственно.
Обозначают число «золотого сечения» математической буквой (mathbf) (фи).
Мир живой и неживой природы, мир творений человека полон красоты, симметрии и гармонии. Этот мир описывается законом «золотого сечения».
Рассмотрим только несколько примеров, где присутствует и используется правило «золотого сечения».
Считается, что длина фаланг пальцев и длина кисти руки, средний палец и мизинец, или высота лица и расстояние от кончика подбородка до центральной точки соединения губ у пропорционального человека находятся в определенных отношениях, соответствуя правилу «золотого сечения».
Форма тела ящериц, стрекоз, бабочек соответствует закону «золотого сечения»: отношение грудной и брюшной части тела приближенно равны значению «золотого сечения».
Спиралевидная форма ракушек тоже описывается числом (mathbf) (фи).
«Золотая пропорция» была обнаружена в египетских пирамидах, произведениях искусства, архитектуре и применяется до сих пор в разных областях жизни человека
Пройти тест и получить оценку можно после входа или регистрации
Видео:ПРОПОРЦИЯ 6 класс математика отношения и пропорцииСкачать

Как решать пропорции — правила, методы и примеры вычислений
Математические операции необходимы не только для расчета каких-либо величин в научной сфере и во время учебы, но и в повседневной жизни. Многие люди сталкиваются с пропорциями. Решать их несложно, но если не знать свойств и правил, можно выполнить неверные вычисления. Специалисты рекомендуют получить теоретические знания, а затем перейти к их практическому применению.
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Общие сведения
Изучение какого-либо термина в математике начинается с определения. Пропорцией вида x / y = v / z (x: y = v: z) называется равенство отношений двух чисел. Она представлена в виде правильной дроби, и состоит из следующих элементов, которые называются крайними (x и z) и средними (y и v) членами.
Следует отметить, что в некоторых сферах пропорциональная зависимость может быть представлена в немного другом виде. В этом случае знак равенства не указывается. Для удобства используется символ деления «:». Записывается в таком виде: a: b: c. Объяснение такой записи очень простое: для приготовления какого-либо вещества нужно использовать «а» частей одного компонента, b — другого и с — третьего.
Знак равенства не имеет смысла указывать, поскольку этот тип пропорциональной зависимости является абстрактным. Неизвестно, какой результат получится на выходе. Если взять за единицу измерения массу в кг, то и конечный результат получится в кг. В этом случае решать пропорцию не нужно — достаточно просто подставить данные, и получить результат.
Бывают случаи, когда следует посчитать пропорцию в процентах. Пример — осуществление некоторых финансовых операций.
Сферы применения
Пропорция получила широкое применение в физике, алгебре, геометрии, высшей и прикладной математике, химии, кулинарии, фармацевтике, медицине, строительстве и т. д. Однако ее нужно применять только в том случае, когда элементы соотношения не подчиняются какому-либо закону (методика исследования величин такого типа будет рассмотрена ниже), и не являются неравенствами.
В алгебре существует класс уравнений, представленных в виде пропорции. Они бывают простыми и сложными. Для решения последних существует определенный алгоритм. Кроме того, в геометрии встречается такие термин, как «гомотетия» или коэффициент подобия. Он показывает, во сколько раз увеличена или уменьшена фигура относительно оригинала.
Масштаб в географии является также пропорцией, поскольку он показывает количество см или мм, которые содержатся в какой-либо единице, зависящей от карты (например, в 1 см = 10 км). Специалисты применяютправило пропорции в высшей и прикладной математике. Расчет количества реактивов, вступающих в реакцию, для получения другого вещества применяется также пропорциональная зависимость.
Каждая хозяйка также применяет это соотношение для приготовления различных блюд и консерваций. В этом случае пропорция имеет немного другой вид: 1:2. Все компоненты берутся частями с одинаковыми размерностями или единицами измерения. Например, на 1 кг клубники необходимо 2 кг сахара. Расшифровывается такое соотношение следующим образом: 1 часть одного и 2 части другого компонентов.
В фармацевтике она также применяется, поскольку необходимо очень точно рассчитать массовую долю для каждого компонента лекарственного препарата. В медицине используется пропорциональная зависимость для назначения лекарства больному, дозировка которого зависит от массы тела человека.
Для приготовления различных строительных смесей она также используется, однако у нее такой же вид, как и для кулинарии. Например, для приготовления бетона М300 необходимы такие компоненты: цемент (Ц), щебень (Щ), песок (П) и вода (В). Далее следует воспользоваться таким соотношением, в котором единицей измерения является ведро: 1: 5: 3: 0,5. Запись расшифровывается следующим образом: для приготовления бетонной смеси необходимо 1 ведро цемента, 5 щебня, 3 песка и 0,5 воды.
Основные свойства
Для решения различных задач нужно знать основные свойства пропорции. Они действуют только для соотношения x / y = v / z. К ним можно отнести следующие формулы:
Первое свойство позволяет перевернуть правильные дроби соотношений двух величин. Это следует делать одновременно для левой и правой частей. Умножение по типу «крест-накрест» считается главным соотношением. С помощью его решаются уравнения и упрощаются выражения, в которых нужно избавиться от дробных частей. Найти неизвестный член пропорции можно также с помощью второго свойства, формулировка которого следующая: произведение крайних эквивалентно произведению средних элементов (членов).
Очень часто члены соотношения необходимо переставить для оптимизации вычислений. Для этого применяется свойство перестановки. При этом следует внимательно подставлять значения в формулу, поскольку неправильные действия могут существенно исказить результат решения. Этого можно не заметить. Для осуществления проверки следует подставить значение неизвестной в исходную пропорцию. Если равенство соблюдается, то получен верный результат. В противном случае необходимо найти ошибку или повторить вычисления.
Увеличение или уменьшение пропорции следует производить по четвертому свойству. Основной принцип: равенство сохраняется в том случае, когда уменьшение или увеличение числителя происходит на значение, которое находится в знаменателе. Нельзя отнимать от пропорции (от числителя и знаменателя равные числовые значения), поскольку соотношение не будет выполняться. Это является распространенной ошибкой, которая влечет за собой огромные погрешности при расчетах или неверное решение экзаменационных заданий.
Составить пропорцию можно с помощью вычитания и сложения. Этот прием применяется редко, но в некоторых заданиях может использоваться. Суть его заключается в следующем: отношение суммы крайнего и среднего элемента к суммарному значению других крайнего и среднего членов, которое равно отношению крайнего к среднему значению. Однако не ко всем выражениям можно применять свойства пропорции. Следует рассмотреть методику их определения.
Видео:Пропорции, 6 класс. Решение задач.Скачать

Методика исследования
Пропорция применима только к линейным законам изменения величин. Примером этого является поведение простой тригонометрической функции z = sin (p). Величина «z» — зависимая переменная, которая называется значением функции. Переменная «p» — независимая величина или аргумент. В данном контексте она принимает значения углов в градусах. Для демонстрации того, что пропорция «не работает» необходимо подставить некоторые данные.
Кроме того, нужна таблица значений тригонометрических функций некоторых углов. Необходимо предположить, что p = 30, тогда z = sin (30) = 0,5. По свойству пропорции можно найти значение функции при р = 60, не используя таблицу. Для этого нужно составить пропорцию с неизвестным: 30 / 0,5 = 60 / х. Чтобы найти х («икс»), нужно воспользоваться свойством умножения «крест-накрест»: 60 * 0,5 = 30 * х. Уравнение решается очень просто: х = 60 * 0,5 / 30 = 30 / 30 = 1. Ответ получен очень быстро, и нет необходимости смотреть табличное значение.
В этом случае не так все просто. Если воспользоваться вышеописанной таблицей, то z = sin (60) = [3^(½)] / 2. Полученное значение не равно 1. Причина несоответствия — нелинейность функции. Математики для облегчения вычислений предлагают методику определения нелинейных выражений. Она состоит из следующих положений:
По таким правилам были исследовано огромное количество функций. К нелинейным относятся следующие: прямые и обратные тригонометрические, гиперболические, показательные, логарифмические и сложные математические, состоящие из нелинейных зависимостей.
К прямым тригонометрическим относятся sin (p), cos (p), tg (p) и ctg (p), а к обратным — arcsin (p), arccos (p), arctg (p) и arcctg (p). Следует отметить, что гиперболическими являются sh, ch, th, cth, sech и csch. Показательная — z = a^y, а логарифмической — функция, имеющая операцию логарифмирования. Простые линейные могут объединяться с нелинейными. В таких случаях правило пропорции также не соблюдается.
Видео:Подробно! Пропорции. Уравнения. Математика 6 класс. Много примеров.Скачать

Универсальный алгоритм
Алгоритм позволяет решать уравнения, и найти неизвестный член пропорции. Для его реализации следует знать теорию о пропорциях, и методику обнаружения нелинейных функций. Он состоит из нескольких шагов, которые помогут правильно вычислить необходимую величину:
Существуют различные приложения, позволяющие решить пропорцию. Онлайн-калькулятор позволяет вычислить неизвестный компонент очень быстро. Кроме того, результат вычислений отображается после проведения расчетов. Для реализации последнего пункта необходимо рассмотреть некоторые типы равенств с неизвестными.
Видео:УРАВНЕНИЯ С ПРОПОРЦИЕЙ. Примеры | МАТЕМАТИКА 6 классСкачать

Уравнения с пропорцией
Существуют уравнения в виде обыкновенной дроби, в которых необходимо найти неизвестную величину. Для этого нужно рассмотреть основные их виды:
Различаются они степенным показателем. У первого типа степень переменной соответствует 1, второго — двойке, третьего — тройке и четвертого — четверке. При решении таких типов нужно выписать знаменатели отдельно, и решить их. Такие корни не являются решением исходной пропорции, поскольку знаменатели должны быть отличны от нулевого значения.
Решение линейного типа сводится к применению правила «крест-накрест». После чего нужно руководствоваться четвертым пунктом универсального алгоритма. Квадратное уравнение (ap 2 + bp + c = 0) решается при помощи разложения на множители (существует высокая вероятность сокращения степени с последующим упрощением выражения) или с использованием дискриминанта (D = b 2 — 4ac). Корни зависят от его значения:
Решение уравнений в виде пропорции осуществляется по такому же принципу. При этом рекомендуется использовать любые свойства. Необходимо проходить процесс обучения постепенно. Начинать нужно с простых примеров, а затем практиковаться на сложных заданиях. Первый тип был рассмотрен выше на примере sin (p).
Итак, необходимо решить уравнение [(t — 5) / (t — 2)] = [(t — 5) / (t — 1)]. Для начала следует определить тип функций каждого из элементов. Просмотрев список нелинейных выражений, можно сделать вывод о том, что все члены пропорции являются линейными. Далее нужно решить равенства с неизвестными, находящихся в знаменателях: t1 = 2 и t2 = 1. Корни не являются решениями уравнения.
Затем следует воспользоваться третьим пунктом алгоритма: (t — 5)(t — 1) = (t — 2)(t — 5). Если раскрыть скобки, то должно получиться такое равенство: t 2 — t — 5t + 5 =t 2 -5t -2t + 10. Перенести все слагаемые в левую сторону с противоположными знаками: t 2 — t — 5t + 5 + 5t — t 2 — 10 + 2t = 0. Приведя подобные слагаемые, выражение будет иметь такой вид: t = 5. Решением пропорции является значение t = 5.
Таким образом, для решения пропорций необходимо знать основные свойства, определение типа выражения по методике и алгоритм расчета.
💡 Видео
Как решить уравнение методом пропорций?Скачать

6 класс, 21 урок, ПропорцииСкачать

6 кл.Пропорция.Решение уравненияСкачать

Решение уравнений, 6 классСкачать

Пропорции, 6 классСкачать

Решение задач на проценты способом пропорции. 6 класс.Скачать