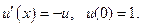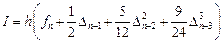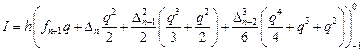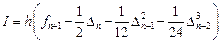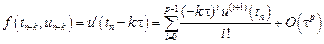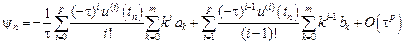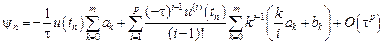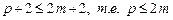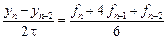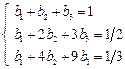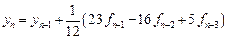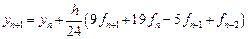Рассмотрим задачу Коши для системы обыкновенных дифференциальных уравнений $$ begin tag frac &= f_i (t, u_1, u_2, ldots, u_n), quad t > 0\ tag u_i(0) &= u_i^0, quad i = 1, 2, ldots, m. end $$
Используя векторные обозначения, задачу (1), (2) можно записать как задачу Коши $$ begin tag frac<d pmb> &= pmb(t, pmb), quad t > 0, \ tag pmb(0) &= pmb_0 end $$ В задаче Коши необходимо по известному решению в точке ( t = 0 ) необходимо найти из уравнения (3) решение при других ( t ).
- Численные методы решения задачи Коши
- Явный метод Эйлера
- Программная реализация явного метода Эйлера
- Неявный метод Эйлера
- Программная реализация неявного метода Эйлера
- Методы Рунге—Кутта
- Многошаговые методы
- Жесткие системы ОДУ
- Предиктор-корректор или модифицированный метод Эйлера для решения дифференциального уравнения
- Общая формулировка многошаговых методов
- 📸 Видео
Видео:3_02. Алгоритмы решения ОДУСкачать

Численные методы решения задачи Коши
Существует большое количество методов численного решения задачи (3), (4). Вначале рассмотрим простейший явный метод Эйлера и его программную реализацию. Затем будут представлены методы Рунге—Кутта и многошаговые методы.
При построении численных алгоритмов будем считать, что решение этой дифференциальной задачи существует, оно единственно и обладает необходимыми свойствами гладкости.
Идея численных методов решения задачи (3), (4) состоит из четырех частей:
1. Вводится расчетная сетка по переменной ( t ) (время) из ( N_t + 1 ) точки ( t_0 ), ( t_1 ), ( ldots ), ( t_ ). Нужно найти значения неизвестной функции ( pmb ) в узлах сетки ( t_n ). Обозначим через ( pmb^n ) приближенное значение ( pmb(t_n) ).
2. Предполагаем, что дифференциальное уравнение выполнено в узлах сетки.
3. Аппроксимируем производные конечными разностями.
4. Формулируем алгоритм, который вычисляет новые значения ( pmb^ ) на основе предыдущих вычисленных значений ( pmb^k ), ( k 0 ) при ( tauto 0 ).
Видео:Решение системы дифференциальных уравнений методом ЭйлераСкачать

Явный метод Эйлера
Проиллюстрируем указанные шаги. Для начала введем расчетную сетку. Очень часто сетка является равномерной, т.е. имеет одинаковое расстояние между узлами ( t_n ) и ( t_ ): $$ omega_tau = . $$
Затем, предполагаем, что уравнение выполнено в узлах сетки, т.е.: $$ pmb^prime (t_n) = pmb(t_n, u(t_n)), quad t_n in omega_tau. $$
Заменяем производные конечными разностями. С этой целью, нам нужно знать конкретные формулы, как производные могут быть аппроксимированы конечными разностями. Простейший подход заключается в использовании определения производной: $$ pmb^prime(t) = lim_ frac<pmb(t+tau) — pmb(t)>. $$
В произвольном узле сетки ( t_n ) это определение можно переписать в виде: $$ begin pmb^prime(t_n) = lim_ frac<pmb(t_n+tau) — pmb(t_n)>. end $$ Вместо того, чтобы устремлять шаг сетки к нулю, мы можем использовать малый шаг ( tau ), который даст численное приближение ( u^prime(t_n) ): $$ begin pmb^prime(t_n) approx frac<pmb^ — pmb^>. end $$ Такая аппроксимация известна как разностная производная вперед и имеет первый порядок по ( tau ), т.е. ( O(tau) ). Теперь можно использовать аппроксимацию производной. Таким образом получим явный метод Эйлера: $$ begin tag frac<pmb^ — pmb^n> = pmb(t_n, pmb^). end $$
Четвертый шаг заключается в получении численного алгоритма. Из (5) следует, что мы должны знать значение ( y^n ) для того, чтобы решить уравнение (5) относительно ( y^ ) и получить формулу для нахождения приближенного значения искомой функции на следующем временном слое ( t_ ): $$ begin tag pmb^ = pmb^n + tau pmb(t_n, pmb^) end $$
При условии, что у нас известно начальное значение ( pmb^0 = pmb_0 ), мы можем использовать (6) для нахождения решений на последующих временных слоях.
Программная реализация явного метода Эйлера
Выражение (6) может быть как скалярным так и векторным уравнением. И в скалярном и в векторном случае на языке Python его можно реализовать следующим образом
При решении системы (векторный случай), u[n] — одномерный массив numpy длины ( m+1 ) (( m ) — размерность задачи), а функция F должна возвращать numpy -массив размерности ( m+1 ), t[n] — значение в момент времени ( t_n ).
Таким образом численное решение на отрезке ( [0, T] ) должно быть представлено двумерным массивом, инициализируемым нулями u = np.zeros((N_t+1, m+1)) . Первый индекс соответствует временному слою, а второй компоненте вектора решения на соответствующем временном слое. Использование только одного индекса, u[n] или, что то же самое, u[n, :] , соответствует всем компонентам вектора решения.
Функция euler решения системы уравнений реализована в файле euler.py:
Строка F_ = lambda . требует пояснений. Для пользователя, решающего систему ОДУ, удобно задавать функцию правой части в виде списка компонент. Можно, конечно, требовать чтобы пользователь возвращал из функции массив numpy , но очень легко осуществлять преобразование в самой функции решателе. Чтобы быть уверенным, что результат F будет нужным массивом, который можно использовать в векторных вычислениях, мы вводим новую функцию F_ , которая вызывает пользовательскую функцию F «прогоняет» результат через функцию assaray модуля numpy .
Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Неявный метод Эйлера
При построении неявного метода Эйлера значение функции ( F ) берется на новом временном слое, т.е. для решении задачи (5) используется следующий метод: $$ begin tag frac<pmb^ — pmb^n> = pmb(t_, pmb^). end $$
Таким образом для нахождения приближенного значения искомой функции на новом временном слое ( t_ ) нужно решить нелинейное уравнение относительно ( pmb^ ): $$ begin tag pmb^ — tau pmb(t_, pmb^) — y^n = 0. end $$
Для решения уравнения (8) можно использовать, например, метод Ньютона.
Программная реализация неявного метода Эйлера
Функция backward_euler решения системы уравнений реализована в файле euler.py:
Отметим, что для нахождения значения u[n+1] используется функция fsolve модуля optimize библиотеки scipy . В качестве начального приближения для решения нелинейного уравнения используется значение искомой функции с предыдущего слоя u[n] .
Видео:7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

Методы Рунге—Кутта
Одношаговый метод Рунге—Кутта в общем виде записывается следующим образом: $$ begin tag frac<pmb^ — pmb^n> = sum_^s b_i pmb_i, end $$ где $$ begin tag pmb_i = pmbleft( t_n + c_itau, pmb^n + tau sum_^s a_pmb_j right), quad i = 1, 2, ldots, s. end $$ Формула (9) основана на ( s ) вычислениях функции ( pmb ) и называется ( s )-стадийной. Если ( a_ = 0 ) при ( j geq i ) имеем явный метод Рунге—Кутта. Если ( a_ = 0 ) при ( j > i ) и ( a_ ne 0 ), то ( pmb_i ) определяется неявно из уравнения $$ begin tag pmb_i = pmbleft( t_n + c_itau, pmb^n + tau sum_^ a_pmb_j + tau a_ pmb_i right), quad i = 1, 2, ldots, s. end $$ О таком методе Рунге—Кутта говорят как о диагонально-неявном.
Одним из наиболее распространенных является явный метод Рунге-Кутта четвертого порядка: $$ begin tag pmb_1 & = pmb(t_n, pmb^n), &quad pmb_2 &= pmbleft( t_n + frac, pmb^n + tau frac<pmb_1> right),\ pmb_3 &= pmbleft( t_n + frac, pmb^n + tau frac<pmb_2> right), &quad pmb_4 &= pmbleft( t_n + tau, pmb^n + tau pmb_3 right),\ frac<pmb^ -pmb^n> &= frac (pmb_1 + 2pmb_2 + 2pmb_3 + pmb_4) & & end $$
Видео:Сеточные методы решения дифференциальных уравнений в частных производных.Скачать

Многошаговые методы
В методах Рунге—Кутта в вычислениях участвуют значения приближенного решения только в двух соседних узлах ( pmb^n ) и ( pmb^ ) — один шаг по переменной ( t ). Линейный ( m )-шаговый разностный метод записывается в виде $$ begin tag frac sum_^m a_i pmb^ = sum_^ b_i pmb(t_, pmb^), quad n = m-1, m, ldots end $$ Вариант численного метода определяется заданием коэффициентов ( a_i ), ( b_i ), ( i = 0, 1, ldots, m ), причем ( a_0 ne 0 ). Для начала расчетов по рекуррентной формуле (13) необходимо задать ( m ) начальных значений ( pmb^0 ), ( pmb^1 ), ( dots ), ( pmb^ ) (например, можно использовать для их вычисления метод Эйлера).
Различные варианты многошаговых методов (методы Адамса) решения задачи с начальными условиями для систем обыкновенных дифференциальных уравнений могут быть получены на основе использования квадратурных формул для правой части равенства $$ begin tag pmb(t_) — pmb(t_n) = int_^<t_> pmb(t, pmb) dt end $$
Для получения неявного многошагового метода используем для подынтегральной функции интерполяционную формулу по значениям функции ( pmb^ = pmb(t_, pmb^) ), ( pmb^n ), ( dots ), ( pmb^ ), т.е. $$ begin tag frac<pmb^ — pmb^n> = sum_^ b_i pmb(t_, pmb^) end $$
Для интерполяционного метода Адамса (15) наивысший порядок аппроксимации равен ( m+1 ).
Для построения явных многошаговых методов можно использовать процедуру экстраполяции подынтегральной функции в правой части (14). В этом случае приближение осуществляется по значениям ( pmb^n ), ( pmb^ ), ( dots ), ( pmb^ ) и поэтому $$ begin tag frac<pmb^ — pmb^n> = sum_^ b_i pmb(t_, pmb^) end $$
Для экстраполяционного метода Адамса (16) погрешность аппроксимации имеет ( m )-ый порядок.
На основе методов Адамса строятся и схемы предиктор–корректор. На этапе предиктор используется явный метод Адамса, на этапе корректора — аналог неявного метода Адамса. Например, при использовании методов третьего порядка аппроксимации в соответствии с (18) для предсказания решения положим $$ frac<pmb^ — pmb^n> = frac (23 pmb^ -16pmb^ + 5pmb^). $$ Для уточнеия решения (см. (17)) используется схема $$ frac<pmb^ — pmb^n> = frac (9pmb^ + 19pmb^ — 5pmb^ + pmb^). $$ Аналогично строятся и другие классы многошаговых методов.
Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Жесткие системы ОДУ
При численном решении задачи Коши для систем обыкновенных дифференциальных уравнений (3), (4) могут возникнуть дополнительные трудности, порожденные жесткостью системы. Локальные особенности поведения решения в точке ( u = w ) передаются линейной системой $$ begin frac
Пусть ( lambda_i(t) ), ( i = 1, 2, ldots, m ) — собственные числа матрицы $$ begin A(t) = < a_(t) >, quad a_(t) = frac(t, w). end $$ Система уравнений (3) является жесткой, если число $$ begin S(t) = frac <max_|Re lambda_i(t)|> <min_|Re lambda_i(t)|> end $$ велико. Это означает, что в решении присутствуют составляющие с сильно различающимися масштабами изменения по переменной ( t ).
Для численное решения жестких задач используются вычислительные алгоритмы, которые имеют повышенный запас устойчивости. Необходимо ориентироваться на использование ( A )-устойчивых или ( A(alpha) )-устойчивых методов.
Метод называется ( A )-устойчивым, если при решении задачи Коши для системы (3) область его устойчивости содержит угол $$ begin |arg(-mu)| —>
Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Предиктор-корректор или модифицированный метод Эйлера для решения дифференциального уравнения
Для заданного дифференциального уравнения 

найти приближенное решение, используя метод Predictor-Corrector.
Метод Предиктор-Корректор:
Метод предиктор-корректор также известен как метод Модифицированного Эйлера .
В методе Эйлера касательная рисуется в точке, а наклон рассчитывается для заданного размера шага. Таким образом, этот метод лучше всего работает с линейными функциями, но для других случаев остается ошибка усечения. Для решения этой проблемы введен модифицированный метод Эйлера. В этом методе вместо точки среднее арифметическое наклона за интервал 
Таким образом, в методе Predictor-Corrector для каждого шага прогнозируемое значение 




 ,
, здесь h — размер шага для каждого приращения


 затем перейдите к шагу — 1.
затем перейдите к шагу — 1.Как и в этом методе, используется средний уклон, поэтому ошибка значительно уменьшается. Также мы можем повторить процесс коррекции сходимости. Таким образом, на каждом шаге мы уменьшаем ошибку, таким образом, улучшая значение y.
Примеры:
The final value of y at x = 1 is y=2.18147
Реализация: здесь мы рассматриваем дифференциальное уравнение:
// C ++ код для решения дифференциального уравнения
// используя метод Predictor-Corrector или Modified-Euler
// с заданными условиями, y (0) = 0,5, размер шага (h) = 0,2
// найти y (1)
using namespace std;
// рассмотрим дифференциальное уравнение
// для заданных x и y возвращаем v
double f( double x, double y)
double v = y — 2 * x * x + 1;
// предсказывает следующее значение для данного (x, y)
// и размер шага h с использованием метода Эйлера
double predict( double x, double y, double h)
// возвращается значение следующего y (прогнозируемого)
double y1p = y + h * f(x, y);
// исправляет прогнозируемое значение
// используя модифицированный метод Эйлера
double correct( double x, double y,
double x1, double y1,
// (x, y) предыдущего шага
// и x1 — увеличенный x для следующего шага
// и у1 прогнозируется у для следующего шага
double e = 0.00001;
y1c = y + 0.5 * h * (f(x, y) + f(x1, y1));
> while ( fabs (y1c — y1) > e);
// каждая итерация корректирует значение
// of y используя средний уклон
void printFinalValues( double x, double xn,
double y, double h)
double x1 = x + h;
double y1p = predict(x, y, h);
double y1c = correct(x, y, x1, y1p, h);
// на каждой итерации сначала значение
// для следующего шага сначала прогнозируется
// а затем исправлено.
cout «The final value of y at x = «
// здесь x и y являются начальными
// заданное условие, поэтому x = 0 и y = 0.5
double x = 0, y = 0.5;
// конечное значение x, для которого требуется y
printFinalValues(x, xn, y, h);
// Java-код для решения дифференциала
// уравнение с использованием Predictor-Corrector
// или модифицированный метод Эйлера с
// заданные условия, y (0) = 0,5, шаг
// размер (h) = 0,2, чтобы найти y (1)
// рассмотрим дифференциальное уравнение
// для заданных x и y возвращаем v
static double f( double x, double y)
double v = y — 2 * x * x + 1 ;
// предсказывает следующее значение для данного (x, y)
// и размер шага h с использованием метода Эйлера
static double predict( double x, double y, double h)
// возвращается значение следующего y (прогнозируемого)
double y1p = y + h * f(x, y);
// исправляет прогнозируемое значение
// используя модифицированный метод Эйлера
static double correct( double x, double y,
double x1, double y1,
// (x, y) предыдущего шага
// и x1 — увеличенный x для следующего шага
// и у1 прогнозируется у для следующего шага
double e = 0.00001 ;
y1c = y + 0.5 * h * (f(x, y) + f(x1, y1));
while (Math.abs(y1c — y1) > e);
// каждая итерация корректирует значение
// of y используя средний уклон
static void printFinalValues( double x, double xn,
double y, double h)
double x1 = x + h;
double y1p = predict(x, y, h);
double y1c = correct(x, y, x1, y1p, h);
// на каждой итерации сначала значение
// для следующего шага сначала прогнозируется
// а затем исправлено.
DecimalFormat df = new DecimalFormat( «#.#####» );
System.out.println( «The final value of y at x = » +
x + » is : » +df.format(y));
public static void main (String[] args)
// здесь x и y являются начальными
// заданное условие, поэтому x = 0 и y = 0.5
double x = 0 , y = 0.5 ;
// конечное значение x, для которого требуется y
printFinalValues(x, xn, y, h);
// Этот код предоставлен mits
# Python3 код для решения дифференциального уравнения
# с использованием метода Predictor-Corrector или Modified-Euler
# с заданными условиями, y (0) = 0,5, размер шага (h) = 0,2
# найти y (1)
# рассмотрим дифференциальное уравнение
# для заданных x и y, вернуть v
v = y — 2 * x * x + 1 ;
# предсказывает следующее значение для данного (x, y)
# и размер шага h методом Эйлера
def predict(x, y, h):
# значение следующего y (прогнозируемого) возвращается
y1p = y + h * f(x, y);
# исправляет прогнозируемое значение
# с использованием модифицированного метода Эйлера
def correct(x, y, x1, y1, h):
# (x, y) предыдущего шага
# и x1 — увеличенный x для следующего шага
# и y1 прогнозируется y для следующего шага
while ( abs (y1c — y1) > e + 1 ):
y1c = y + 0.5 * h * (f(x, y) + f(x1, y1));
# каждая итерация корректирует значение
# у, используя средний наклон
def printFinalValues(x, xn, y, h):
y1p = predict(x, y, h);
y1c = correct(x, y, x1, y1p, h);
# на каждой итерации сначала значение
# для следующего шага сначала прогнозируется
# а затем исправлено.
print ( «The final value of y at x =» ,
if __name__ = = ‘__main__’ :
# здесь x и y являются начальными
# заданное условие, поэтому x = 0 и y = 0.5
# конечное значение x, для которого требуется y
printFinalValues(x, xn, y, h);
# Этот код предоставлен Rajput-Ji
// C # код для решения дифференциала
// уравнение с использованием Predictor-Corrector
// или модифицированный метод Эйлера с
// заданные условия, y (0) = 0,5, шаг
// размер (h) = 0,2, чтобы найти y (1)
// рассмотрим дифференциальное уравнение
// для заданных x и y возвращаем v
static double f( double x, double y)
double v = y — 2 * x * x + 1;
// предсказывает следующее значение для данного (x, y)
// и размер шага h с использованием метода Эйлера
static double predict( double x, double y, double h)
// возвращается значение следующего y (прогнозируемого)
double y1p = y + h * f(x, y);
// исправляет прогнозируемое значение
// используя модифицированный метод Эйлера
static double correct( double x, double y,
double x1, double y1,
// (x, y) предыдущего шага
// и x1 — увеличенный x для следующего шага
// и у1 прогнозируется у для следующего шага
double e = 0.00001;
y1c = y + 0.5 * h * (f(x, y) + f(x1, y1));
while (Math.Abs(y1c — y1) > e);
// каждая итерация корректирует значение
// of y используя средний уклон
static void printFinalValues( double x, double xn,
double y, double h)
double x1 = x + h;
double y1p = predict(x, y, h);
double y1c = correct(x, y, x1, y1p, h);
// на каждой итерации сначала значение
// для следующего шага сначала прогнозируется
// а затем исправлено.
Console.WriteLine( «The final value of y at x = » +
x + » is : » + Math.Round(y, 5));
static void Main()
// здесь x и y являются начальными
// заданное условие, поэтому x = 0 и y = 0.5
double x = 0, y = 0.5;
// конечное значение x, для которого требуется y
printFinalValues(x, xn, y, h);
// Этот код предоставлен mits
// PHP-код для решения дифференциального уравнения
// используя Predictor-Corrector или Modified-Euler
// метод с заданными условиями, y (0) = 0,5,
// размер шага (h) = 0,2, чтобы найти y (1)
// рассмотрим дифференциальное уравнение
// для заданных x и y возвращаем v
function f( $x , $y )
$v = $y — 2 * $x * $x + 1;
// предсказывает следующее значение для данного (x, y)
// и размер шага h с использованием метода Эйлера
function predict( $x , $y , $h )
// возвращается значение следующего y (прогнозируемого)
$y1p = $y + $h * f( $x , $y );
// исправляет прогнозируемое значение
// используя модифицированный метод Эйлера
function correct( $x , $y , $x1 , $y1 , $h )
// (x, y) предыдущего шага и
// х1 — увеличенный х для следующего шага
// и у1 прогнозируется у для следующего шага
$y1c = $y + 0.5 * $h * (f( $x , $y ) +
> while ( abs ( $y1c — $y1 ) > $e );
// каждая итерация корректирует
// значение y с использованием среднего наклона
function printFinalValues( $x , $xn , $y , $h )
$y1p = predict( $x , $y , $h );
$y1c = correct( $x , $y , $x1 , $y1p , $h );
// на каждой итерации сначала значение
// для следующего шага сначала прогнозируется
// а затем исправлено.
echo «The final value of y at x = » . $x .
» is : » . round ( $y , 5) . «n» ;
// здесь x и y являются начальными
// заданное условие, поэтому x = 0 и y = 0.5
// конечное значение x, для которого требуется y
printFinalValues( $x , $xn , $y , $h );
// Этот код предоставлен mits
?>
Видео:19. Метод вариации произвольных постоянных. Линейные неоднородные диф уравнения 2-го порядкаСкачать

Общая формулировка многошаговых методов
Многошаговые методы
Решения задачи коши
9.1. Метод “предиктор-корректор” 2
9.2. Общая формулировка многошаговых методов 4
9.3. Устойчивость и сходимость разностных методов 7
9.1. Метод “предиктор-корректор”
В одношаговых методах значение yn+1 определяется лишь значениями tn, yn и значением шага приращения аргумента h. В многошаговых методах используется также информация в предыдущих точках yn-1, yn-2,
Многошаговые методы строятся на равномерной сетке
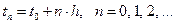
Обозначим: 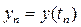
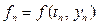
Линейный m-шаговый метод можно описать формулой:

Многошаговые методы не являются самостартующими. Для использования m-шагового метода необходимо предварительно задать m предыдущих значений y. Однако после того как многошаговый метод стартует, он работает быстрее, чем одношаговый. Например, при использовании метода Рунге-Кутта-Фельберга на каждом шаге приращения аргумента требуется шесть раз вычислять правую часть дифференциального уравнения 
Еще одним ограничением использования многошаговых методов является наличие равномерной сетки. Однако это ограничение легко преодолевается, например, с помощью интерполяции.
Многошаговые методы используются при решении жестких уравнений.
Порядок многошагового метода может выбираться автоматически и динамически изменяться.
Если 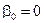
Если 
Частным случаем многошаговых методов являются методы Адамса:
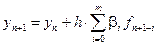
Методы Адамса также могут быть явными и неявными.
Трудности использования неявной формулы преодолевается в методе Предиктор–Корректор. В этом методе значение неизвестной функции в каждой точке сетки вычисляется дважды. Сначала вычисляется новое значение неизвестной функции 

Простейшим примером метода Предиктор–Корректор является второй модифицированный метод Эйлера, который можно описать с помощью последовательности формул:

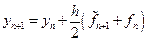
Метод Эйлера является одношаговым методом. Для построения многошаговых методов вновь используем утверждение: решение задачи Коши эквивалентно решению интегрального уравнения
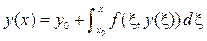
Для приближенного решения задачи Коши аппроксимируем подынтегральную функцию в формуле (9.3) с помощью интерполяционного многочлена. Интерполяционный многочлен Ньютона степени m для интерполирования назад от точки xn можно записать следующим образом

В формуле (9.4) 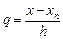

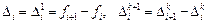

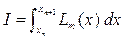
Найдем вначале формулы для двухшагового метода m=2. В качестве подынтегральной функции в формуле (9.6) будем использовать интерполяционный многочлен Ньютона первой степени.
Для вывода формулы предиктор вычислим интеграл (9.6) на отрезке экстраполяции 

и 
Подставив найденное значение интеграла в формулу (9.3), получим экстраполяционную формулу – формулу предиктор:

При выводе формулы корректор используем многочлен Ньютона для интерполирования от точки xn+1. Соответственно, в формуле (9.7) все индексы нужно увеличить на 1, а пределы интегрирования изменить на 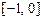
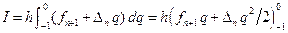
Подставив найденное значение интеграла в формулу (9.3), получим интерполяционную формулу – формулу корректор:
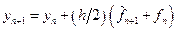
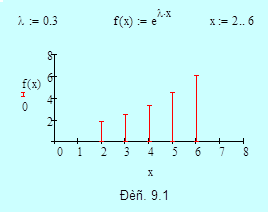
С помощью двухшагового метода предиктор-корректор найдем решение начальной задачи:
Точное решение представляет собой экспоненту 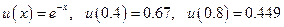
Выберем шаг приращения 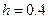
Начальное условие: 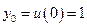
Дополнительное условие: 
С помощью формул (9.8) и (9.10) вычислим значение 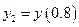
По формуле предиктор получаем: 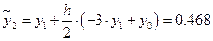
По формуле корректор уточняем решение: 
Для сравнения приведем расчеты значения 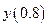

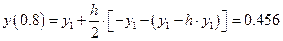
На практике обычно применяется четырехшаговый метод Адамса. Найдем формулы для четырехшагового метода. Повторяем весь ход рассуждений, использованных при выводе формул 2-шагового метода, но в отличие от предыдущего используем теперь многочлен Ньютона третьей степени.
Вывод формулы предиктор.
Подставив найденное значение интеграла в формулу (9.3), получим с учетом выражений (9.5) для конечных разностей формулу предиктор – формулу Адамса-Башфорта (Adams-Bashforth):
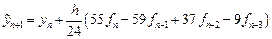
Вывод формулы корректор.
Аналогично предыдущему с учетом (9.3) и (9.5) получим формулу корректор – формулу Адамса-Мультона (Adams-Moulton):
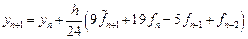
Общая формулировка многошаговых методов
Для решения задачи Коши
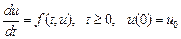
введем сетку с постоянным шагом 

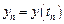

Линейным m-шаговым разностным методом называется система разностных уравнений
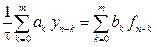
где 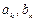
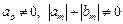
Уравнение (9.14) представляет собой рекуррентное соотношение, выражающее новое значение 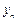
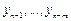
Заметим, что коэффициенты уравнения (9.14) определены с точностью до множителя. Для устранения неоднозначности будем считать, что выполнено условие нормировки

Метод называется явным, если 
Если 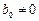
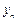

Это уравнение можно решить методом Ньютона, в качестве начального приближения взяв 
Погрешностью аппроксимации на решении или невязкой разностного метода (9.14) называется функция
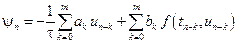
Функция невязки получается в результате подстановки точного решения дифференциального уравнения в разностное уравнение (9.14).
Подставим эти разложения в формулу для невязки
Изменим порядок суммирования. При этом во второй сумме будем суммировать по индексу i от 1 до p, соответственно уменьшив всюду индекс i на единицу.
Объединим суммы, выделив в первой сумме отдельно слагаемое с j=0.
Отсюда следует, что погрешность метода будет иметь порядок p, если выполнены условия:
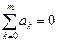
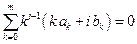

Заметим что, если в системе (9.17) отбросить последние s уравнений, то порядок метода понизится на s.
Итак, получили систему уравнений для коэффициентов ak, bk. К этим уравнениям нужно добавить еще условие нормировки (9.15): 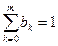
Для неявного метода имеем 2m+2 неизвестных: 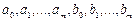
– для неявного метода порядок аппроксимации не превышает 2m.
Для явного метода имеем 2m+1 неизвестных: 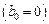
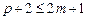
Преобразуем систему уравнений для коэффициентов ak, bk. С учетом условия нормировки уравнение 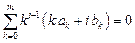
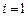
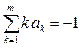
Окончательно получаем систему уравнений для коэффициентов линейного m-шагового разностного метода общего вида:
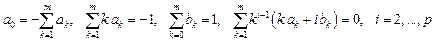
На практике часто используются методы Адамса, которые описываются формулой
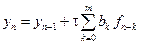
Для методов Адамса в системе (9.18) остаются только уравнения, определяющие коэффициенты bk.

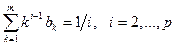
Имеем p уравнений. В случае неявного метода Адамса имеется m+1 неизвестных: 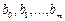
Рассмотрим варианты двухшаговых методов m=2. Максимальный порядок двухшагового метода равен p=4, так что можно написать следующую систему уравнений.
Ограничившись первыми четырьмя уравнениями этой системы, можно построить методы 2-го порядка. Если использовать пять уравнений, получим методы 3-го порядка. Система из шести уравнений определяет единственный двухшаговый метод 4-го порядка.
Варианты методов второго порядка.
1) Положим 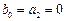
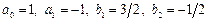

2) Положив 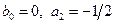

3) Положив 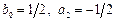
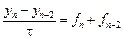
Варианты методов третьего порядка.
1) Положив 
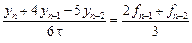
2) Если выбрать 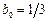

3) Выбрав 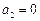
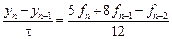
Метод четвертого порядка получим, используя все шесть уравнений:
Явный трехшаговый метод имеет порядок p=3. В соответствии с формулами (9.20) для нахождения коэффициентов bk имеем систему уравнений, включающую условие нормировки и еще два уравнения для двух значений i: 
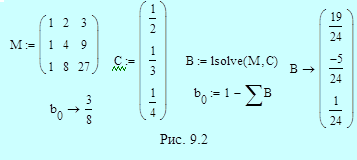
Неявный метод имеет четвертый порядок, и для коэффициентов 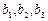
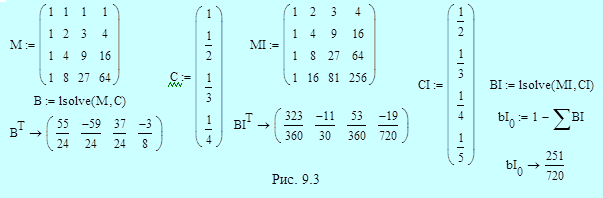 |
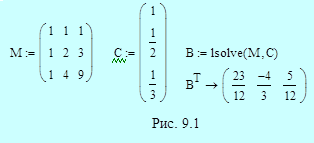
Пример 9.4. На рис. 9.3 приведено решение системы уравнений для коэффициентов явного и неявного четырехшаговых методов Адамса. Решение аналогично решению в примере 9.2 для трехшаговых методов. Обозначения M, C и B относятся к явному методу; обозначения MI, CI, BI и bI0 используются для описания неявного метода. Получаем в итоге:
- явный метод четвертого порядка (формула Адамса-Башфорта)
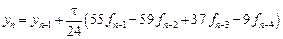
- неявный метод пятого порядка
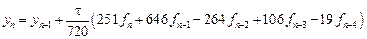
📸 Видео
16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

9. Метод вариации произвольной постоянной ( метод Лагранжа ). Линейные дифференциальные уравнения.Скачать

Решение ДУ.Операционный методСкачать

Видеоурок "Нахождение частных решений по виду правой части"Скачать

Практика 1 ИзоклиныСкачать

13. Как решить дифференциальное уравнение первого порядка?Скачать

3_05. Многошаговые алгоритмы решения ОДУСкачать